Difference between revisions of "Exercise 2.6: Cyclic Prefix"
| Line 4: | Line 4: | ||
}} | }} | ||
| − | [[File: | + | [[File:EN_Bei_A_2_6.png|right|frame|$\rm DSL/DMT$ realization with cyclic prefix]] |
| − | |||
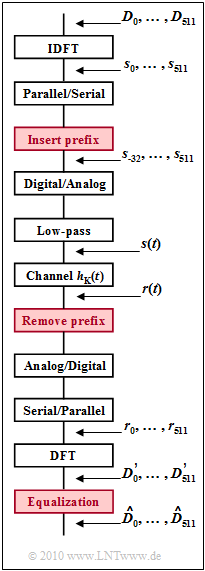
A major advantage of $\rm DSL/DMT$ is the simple equalization of channel distortion by inserting a guard interval and a cyclic prefix. The diagram shows a simplified block diagram, where the prefix used for equalization of the channel frequency response | A major advantage of $\rm DSL/DMT$ is the simple equalization of channel distortion by inserting a guard interval and a cyclic prefix. The diagram shows a simplified block diagram, where the prefix used for equalization of the channel frequency response | ||
Latest revision as of 18:37, 25 March 2023
A major advantage of $\rm DSL/DMT$ is the simple equalization of channel distortion by inserting a guard interval and a cyclic prefix. The diagram shows a simplified block diagram, where the prefix used for equalization of the channel frequency response
- $$H_{\rm K}(f) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm K}(t)$$
required components are highlighted in red.
For the $\rm ADSL/DMT$ downstream the following parameters apply:
- With each frame, the subchannels $k = 64$, ... , $255$ at the carrier frequencies $f_k = k \cdot f_0$ occupied with the QAM symbols $D_k$ . Because of the reservation of the lowest frequencies for ISDN and for upstream $D_0 =$ ... $= D_{63} = 0$.
- The fundamental frequency is chosen to $f_0 = 4.3125 \ \rm kHz$ and the frame duration is $T = 1/f_0 \approx 232 \ {\rm µ s}$. These values result from the requirement that $4000$ frames should be transmitted per second and a synchronization frame is inserted after every $68$–th frame.
- After occupying the upper coefficients $(k = 257$, ... , $448)$ according to $D_k = D_{512-k}^{\ast}$ the entire block $D_0$, ... , $D_{511}$ is fed to an Inverse Discrete Fourier Transform $\rm (IDFT)$ . The time coefficients are then $s_0$, ... , $s_{511}$.
- To avoid impulse interference - also called inter-symbol interference $\rm (ISI)$ - between adjacent frames, a guard interval of duration $T_{\rm G}$ is inserted between two frames. The frame spacing must be at least as large as the "length" $T_{\rm K}$ of the impulse response.
- In addition, the IDFT output values $(s_{480}$, ... , $s_{511})$ are duplicated, prefixed as $(s_{-32}$, ... , $s_{-1})$ to the output vector $(s_0$, ... , $s_{511})$ and transmitted in the guard interval. This is called the "cyclic prefix". Thus, the subcarriers of a frame do not interfere with each other either, which means that there is not only no $\rm ISI$, but also no inter-carrier interference $\rm (ICI)$.
Hints:
- This exercise belongs to the chapter "Methods to Reduce the Bit Error Rate in DSL".
- Reference is made in particular to the page "Inserting guard interval and cyclic prefix".
- In the questions $s_k(t)$ denotes the (continuous-time) waveform when only the coefficient $D_k$ of the carrier at $f_k = k \cdot f_0$ is different from zero.
Questions
Solution
- $$T_{\rm G} = \frac{32}{512} \cdot T = \frac{232\,{\rm µ s}}{16} \hspace{0.15cm}\underline{= 14.5\,{\rm µ s} }\hspace{0.05cm}.$$
(2) Intersymbol interference (ISI) and intercarrier interference (ICI) are avoided as long as the length $T_{\rm K}$ of the channel impulse response is not greater than the length $T_{\rm G}$ of the guard interval:
- $$T_{\rm K,\hspace{0.08cm} max} \le T_{\rm G} \hspace{0.15cm}\underline{= 14.5\,{\rm µ s}} \hspace{0.05cm}.$$
(3) The correct solution is proposed solution 2.
- For the output coefficients of the DFT, in the noise-free case:
- $$D_k\hspace{0.01cm}' = D_k \cdot H_{\rm K} ( f = f_k), \hspace{0.2cm} f_k = k \cdot f_0 \hspace{0.05cm}.$$
- The individual bins can be equalized individually by multiplying by $H_{\rm K}^{-1}(f = f_k)$. Thus, for all $k = 1$, ... , $K$:
- $$\hat{D}_k = D_k \hspace{0.05cm}.$$
- Statement 3 is false: rather, the rate is lower by a factor of $T/(T + T_{\rm G}) = 16/17$ than without guard interval and cyclic prefix.
- However, this small loss is readily accepted, since the ease of equalization more than compensates for this disadvantage.
(4) Correct here is only the proposed solution 2:
- This would not prevent so-called intercarrier interference, that is, the subcarriers of a frame would then no longer be orthogonal to each other, since the convolution of the harmonic oscillation limited in time to $T$ with the impulse response does not yield an si function, as is the case with "ideal channel".
- Thus, the coefficient $D_k$ at $k \cdot f_0$ also affects the spectral values at $\kappa \cdot f_0$ in the neighborhood $(\kappa \neq k)$.
(5) The correct solutions 1 and 2 are:
- The magnitude and phase of $s_k(t)$ is very well changed by $h_{\rm K}(t)$, corresponding to the value $H_{\rm K}(f = f_k)$ of the frequency response.
- However, this error can be corrected in a simple way (and independently of the other bins) by the equalizer on the receiver side.