Error Probability for Baseband Transmission

1. Digital Signal Transmission
2. Digitalsignalübertragung bei idealisierten Bedingungen
3. Error Probability for Baseband Transmission

• Previous page
• Next page

• Previous page
• Next page

Definition der Bitfehlerwahrscheinlichkeit

Zur Definition der Bitfehlerwahrscheinlichkeit

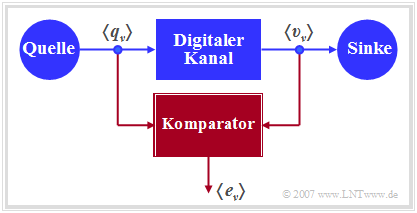
Die Grafik zeigt ein sehr einfaches, aber allgemeingültiges Modell eines binären Übertragungssystems. Dieses lässt sich wie folgt charakterisieren:

• Die Quelle und die Sinke werden durch die beiden Binärfolgen $〈q_ν〉$ und $〈v_ν〉$ beschrieben.
• Das gesamte Übertragungsystem – bestehend aus Sender, Übertragungskanal inklusive Störungen und Empfänger – wird als „Black Box” mit binärem Eingang und binärem Ausgang betrachtet.
• Dieser „Digitale Kanal” wird allein durch die Fehlerfolge $〈e_ν〉$ charakterisiert. Bei fehlerfreier Übertragung des $\nu$–ten Bits $(v_ν = q_ν)$ gilt $e_ν= 0$, andernfalls $(v_ν \ne q_ν)$ wird $e_ν= 1$ gesetzt.

$\text{Definition:}$  Die (mittlere) Bitfehlerwahrscheinlichkeit ist bei einem Binärsystem wie folgt gegeben:

$$p_{\rm B} = {\rm E}[{\rm Pr}(v_{\nu} \ne q_{\nu})]= \overline{ {\rm Pr}(v_{\nu} \ne q_{\nu}) } = \lim_{N \to\infty}\frac{1}{N}\cdot\sum\limits_{\nu=1}^{N}{\rm Pr}(v_{\nu} \ne q_{\nu})\hspace{0.05cm}.$$

Diese statistische Größe ist das wichtigste Beurteilungskriterium eines jeden Digitalsystems.

Die Berechnung als Erwartungswert $\rm E[\text{...}]$ gemäß dem ersten Teil der obigen Gleichung entspricht einer Scharmittelung über die Verfälschungswahrscheinlichkeit ${\rm Pr}(v_{\nu} \ne q_{\nu})$ des $\nu$–ten Symbols, während die überstreichende Linie im rechten Gleichungsteil eine Zeitmittelung kennzeichnet. Beide Berechnungsarten führen – unter der gerechtfertigten Annahme ergodischer Prozesse – zum gleichen Ergebnis, wie im Hauptkapitel 4   ⇒   „Zufallsgrößen mit statistischen Bindungen” des Buches Stochastische Signaltheorie gezeigt wurde.

Auch aus der Fehlerfolge $〈e_ν〉$ lässt sich die Bitfehlerwahrscheinlichkeit als Erwartungswert bestimmen, wobei zu berücksichtigen ist, dass die Fehlergröße $e_ν$ nur die Werte $0$ und $1$ annehmen kann:

$$\it p_{\rm B} = \rm E[\rm Pr(\it e_{\nu}=\rm 1)]= {\rm E}[{\it e_{\nu}}]\hspace{0.05cm}.$$

• Die obige Definition der Bitfehlerwahrscheinlichkeit gilt unabhängig davon, ob es statistische Bindungen innerhalb der Fehlerfolge $〈e_ν〉$ gibt oder nicht.
• Je nachdem ist der Aufwand zur Berechnung von $p_{\rm B}$ unterschiedlich groß und bei einer Systemsimulation müssen unterschiedliche digitale Kanalmodelle herangezogen werden.

Im Hauptkapitel 5 wird gezeigt, dass das sog. BSC–Modell (Binary Symmetrical Channel) statistisch unabhängige Fehler liefert, während für die Beschreibung von Bündelfehlerkanälen auf die Modelle von Gilbert–Elliott [Gil60] und von McCullough [McC68] zurückgegriffen werden muss.

Definition der Bitfehlerquote

Die Bitfehlerwahrscheinlichkeit $p_{\rm B}$ eignet sich zum Beispiel gut für die Konzipierung und Optimierung von Digitalsystemen. Diese ist eine Apriori-Kenngröße, die eine Vorhersage über das Fehlerverhalten eines Nachrichtensystems erlaubt, ohne dass dieses bereits realisiert sein muss.

Dagegen muss zur messtechnischen Erfassung der Qualität eines realisierten Systems oder bei einer Systemsimulation auf die Bitfehlerquote übergegangen werden, die durch den Vergleich von Quellensymbolfolge $〈q_ν〉$ und Sinkensymbolfolge $〈v_ν〉$ ermittelt wird. Diese ist somit eine Aposteriori-Kenngröße des Systems.

$\text{Definition:}$  Die Bitfehlerquote (englisch: Bit Error Rate, BER) ist das Verhältnis aus der Anzahl $n_{\rm B}(N)$ der aufgetretenen Bitfehler $(v_ν \ne q_ν)$ und der Anzahl $N$ der insgesamt übertragenen Symbole:

$$h_{\rm B}(N) = \frac{n_{\rm B}(N)}{N} \hspace{0.05cm}.$$

Im Sinne der Wahrscheinlichkeitsrechnung ist die Bitfehlerquote eine relative Häufigkeit dar; sie wird deshalb auch Bitfehlerhäufigkeit genannt.

• Die Schreibweise $h_{\rm B}(N)$ soll deutlich machen, dass die per Messung oder durch Simulation ermittelte Bitfehlerquote signifikant von dem Parameter $N$ – also der Anzahl der insgesamt übertragenen oder simulierten Symbole – abhängt.
• Nach den elementaren Gesetzen der Wahrscheinlichkeitsrechnung stimmt nur im Grenzfall $N \to \infty$ die Aposteriori–Kenngröße $h_{\rm B}(N\to \infty)$ mit der Apriori–Kenngröße $p_{\rm B}$ exakt überein.
  
  

Der Zusammenhang zwischen Wahrscheinlichkeit und relativer Häufigkeit wird im LernvideoBernoullisches Gesetz der großen Zahlen verdeutlicht.

Bitfehlerwahrscheinlichkeit und Bitfehlerquote beim BSC-Modell

Für die nachfolgenden Herleitungen wird das BSC–Modell (Binary Symmettric Channel) zugrunde gelegt, das in Kapitel 5.2 im Detail beschrieben wird.

• Jedes einzelne Bit wird mit der Wahrscheinlichkeit $p = {\rm Pr}(v_{\nu} \ne q_{\nu}) = {\rm Pr}(e_{\nu} = 1)$ verfälscht, unabhängig von den Fehlerwahrscheinlichkeiten der benachbarten Symbole.
• Die (mittlere) Bitfehlerwahrscheinlichkeit $p_{\rm B}$ ist somit ebenfalls gleich $p$.

Abgeschätzt werden soll, wie genau die Bitfehlerwahrscheinlichkeit $p_{\rm B} = p$ beim BSC-Modell durch die Bitfehlerquote $h_{\rm B}(N)$ approximiert wird. Dies geschieht in mehreren Schritten:

• Die Anzahl der Bitfehler bei der Übertragung von $N$ Symbolen ist eine diskrete Zufallsgröße::

$$n_{\rm B}(N) = \sum\limits_{\it \nu=\rm 1}^{\it N} e_{\nu} \hspace{0.2cm} \in \hspace{0.2cm} \{0, 1, \text{...} , N \}\hspace{0.05cm}.$$

• Bei statistisch unabhängigen Fehlern (BSC) ist $n_{\rm B}(N)$ binominalverteilt. Demzufolge gilt:

$$m_{n{\rm B}}=N \cdot p_{\rm B},\hspace{0.2cm}\sigma_{n{\rm B}}=\sqrt{N\cdot p_{\rm B}\cdot (\rm 1- \it p_{\rm B})}\hspace{0.05cm}.</math>

• Für Mittelwert und Streuung der Bitfehlerquote h_B = n_B/N gilt deshalb:\[m_{h{\rm B}}= \frac{m_{n{\rm B}}}{N} = p_{\rm B}\hspace{0.05cm},\hspace{0.2cm}\sigma_{h{\rm B}}= \frac{\sigma_{n{\rm B}}}{N}= \sqrt{\frac{ p_{\rm B}\cdot (\rm 1- \it p_{\rm B})}{N}}\hspace{0.05cm}.\]
• Nach Moivre und Laplace lässt sich die Binominalverteilung in eine Gaußverteilung überführen:\[f_{h{\rm B}}({h_{\rm B}}) \approx \frac{1}{\sqrt{2\pi}\cdot\sigma_{h{\rm B}}}\cdot {\rm exp} \left[-\frac{(h_{\rm B}-p_{\rm B})^2}{2 \cdot \sigma_{h{\rm B}}^2}\right].\]
• Mit dem Gaußschen Fehlerintergal Q(x) lässt sich somit die Wahrscheinlichkeit p_ε berechnen, dass die per Simulation/Messung über N Symbole ermittelte Bitfehlerquote h_B(N) betragsmäßig um weniger als einen Wert ε von der tatsächlichen Bitfehlerwahrscheinlichkeit p_B abweicht:\[p_{\varepsilon}= {\rm Pr} \left( |h_{\rm B}(N) - p_{\rm B}| < \varepsilon \right) = 1 -2 \cdot {\rm Q} \left( \frac{\varepsilon}{\sigma_{h{\rm B}}} \right)= 1 -2 \cdot {\rm Q} \left( \frac{\varepsilon \cdot \sqrt{N}}{\sqrt{p_{\rm B} \cdot (1-p_{\rm B})}} \right)\hspace{0.05cm}.\]

Dieses Ergebnis ist wie folgt zu interpretieren: Wenn man unendlich viele Versuchsreihen über jeweils N Symbole durchführt, ist der Mittelwert m_hB tatsächlich gleich der gesuchten Fehlerwahrscheinlichkeit p_B. Bei einer einzigen Versuchsreihe wird man dagegen nur eine Näherung erhalten, wobei die jeweilige Abweichung vom Sollwert bei mehreren Versuchsreihen gaußverteilt ist.

: Die Bitfehlerwahrscheinlichkeit betrage p_B = 10^–3 und es ist bekannt, dass die Bitfehler statistisch unabhängig sind. Macht man nun sehr viele Versuchsreihen mit jeweils N = 10⁵ Symbolen, so werden die jeweiligen Ergebnisse h_B entsprechend einer Gaußverteilung um den Sollwert 10^–3 variieren. Die Streuung beträgt dabei

\(\sigma_{h{\rm B}}= \sqrt{{ p_{\rm B}\cdot (\rm 1- \it p_{\rm B})}/{N}}\approx 10^{-4}\hspace{0.05cm}.\)
Die Wahrscheinlichkeit, dass die relative Häufigkeit einen Wert zwischen 0.9 · 10^–3 und 1.1 · 10^–3 (ε = 10^–4) haben wird, ist somit gleich p_ε = 1 – 2 · Q(ε/σ_hB) = 1 – 2 · Q(1) ≈ 68.4%. Soll diese Wahrscheinlichkeit (Genauigkeit) auf 95% gesteigert werden, so müsste N auf 400 000 erhöht werden.

Fehlerwahrscheinlichkeit bei Gaußschem Rauschen (1)

Entsprechend den Voraussetzungen zu diesem Kapitel gehen wir davon aus, dass das Detektionssignal zu den Detektionszeitpunkten wie folgt dargestellt werden kann:\[ d(\nu T) = d_{\rm S}(\nu T)+d_{\rm N}(\nu T)\hspace{0.05cm}. \] Der Nutzanteil wird durch die Wahrscheinlichkeitsdichtefunktion (WDF) f_dS(d_S) beschrieben, wobei wir hier von unterschiedlichen Auftrittswahrscheinlichkeiten p_L = Pr(d_S = –s₀), p_H = Pr(d_S = +s₀) = 1– p_L ausgehen. Die WDF f_dN(d_N) der Störkomponente ist gaußförmig und besitzt die Streuung σ_d.



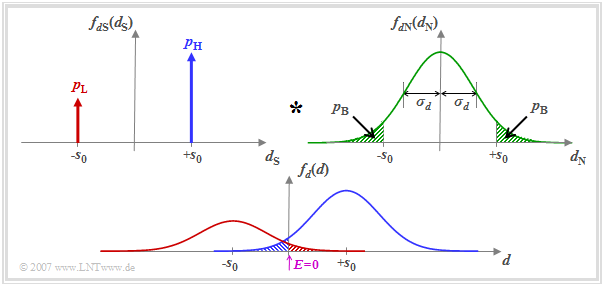
Die WDF f_d(d) der Detektionsabtastwerte d(νT) ergibt sich unter der Voraussetzung, dass d_S(νT) und d_N(νT) statistisch unabhängig voneinander sind („signalunabhängiges Rauschen”), als Faltungsprodukt:

\(f_d(d) = f_{d{\rm S}}(d_{\rm S}) \star f_{d{\rm N}}(d_{\rm N})\hspace{0.05cm}.\)

Der Schwellenwertentscheider mit der Schwelle E = 0 trifft dann eine falsche Entscheidung, wenn

• das Symbol L gesendet wurde (d_S = –s₀) und d > 0 ist (rote schraffierte Fläche), oder
• das Symbol H gesendet wurde (d_S = +s₀) und d < 0 ist (blaue schraffierte Fläche).

Da die Flächen der zwei Gaußkurven zusammen 1 ergeben, gibt die Summe aus der rot und der blau schraffierten Fläche die Bitfehlerwahrscheinlichkeit p_B an. Die beiden grün schraffierten Flächen in der oberen Wahrscheinlichkeitsdichtefunktion f_dN(d_N) sind – jede für sich – ebenfalls gleich p_B.
Die anhand der Grafik veranschaulichten Ergebnisse sollen nun formelmäßig hergeleitet werden. Es gilt\[p_{\rm B} = p_{\rm L} \cdot {\rm Pr}( \upsilon_\nu = \mathbf{H}\hspace{0.1cm}|\hspace{0.1cm} q_\nu = \mathbf{L})+ p_{\rm H} \cdot {\rm Pr}( \upsilon_\nu = \mathbf{L}\hspace{0.1cm}|\hspace{0.1cm} q_\nu = \mathbf{H})\hspace{0.05cm}.\]
Hierbei sind p_L und p_H die Quellensymbolwahrscheinlichkeiten, während die jeweils zweiten, bedingten Wahrscheinlichkeiten Pr(υ_ν | q_ν) die Verfälschungen durch den AWGN–Kanal beschreiben. Aus der Entscheidungsregel des Schwellenwertentscheiders (mit Schwelle E = 0) ergibt sich auch:\[p_{\rm B} = p_{\rm L} \cdot {\rm Pr}( d(\nu T)>0)+ p_{\rm H} \cdot {\rm Pr}( d(\nu T)<0) =\]

\[= p_{\rm L} \cdot {\rm Pr}( d_{\rm N}(\nu T)>s_0)+ p_{\rm H} \cdot {\rm Pr}( d_{\rm N}(\nu T)<-s_0) \hspace{0.05cm}.\]

Die Herleitung wird auf der nächsten Seite fortgesetzt.

Fehlerwahrscheinlichkeit bei Gaußschem Rauschen (2)

Die weitere Herleitung soll nun Schritt für Schritt erfolgen. Ausgegangen wird von der Gleichung:\[p_{\rm B} = p_{\rm L} \cdot {\rm Pr}( d(\nu T)>0)+ p_{\rm H} \cdot {\rm Pr}( d(\nu T)<0) =\]

\[ = p_{\rm L} \cdot {\rm Pr}( d_{\rm N}(\nu T)>s_0)+ p_{\rm H} \cdot {\rm Pr}( d_{\rm N}(\nu T)<-s_0) \hspace{0.05cm}.\]

• Die beiden Überschreitungswahrscheinlichkeiten in obiger Gleichung sind aufgrund der Symmetrie der Gaußschen WDF f_dN(d_N) gleich und es gilt:\[p_{\rm B} = (p_{\rm L} + p_{\rm H}) \cdot {\rm Pr}( d_{\rm N}(\nu T)>s_0) = {\rm Pr}( d_{\rm N}(\nu T)>s_0)\hspace{0.05cm}.\]

Das bedeutet, dass die Bitfehlerwahrscheinlichkeit bei einem Binärsystem mit der Schwelle E = 0 nicht von den Symbolwahrscheinlichkeiten p_L und p_H = 1 – p_L abhängt.

• Die Wahrscheinlichkeit, dass der gaußverteilte Stör– bzw. Rauschterm mit Streuung σ_d größer ist als die NRZ–Sendeimpulsamplitude s₀, ergibt sich zu\[p_{\rm B} = \int_{s_0}^{+\infty}f_{d{\rm N}}(d_{\rm N})\,{\rm d} d_{\rm N} = \frac{\rm 1}{\sqrt{2\pi} \cdot \sigma_d}\int_{ s_0}^{+\infty}{\rm exp} \left [-\frac{d_{\rm N}^2}{2\sigma_d^2} \right ]\,{\rm d} d_{\rm N}\hspace{0.05cm}.\]
• Unter Verwendung des komplementären Gaußschen Fehlerintegrals lautet das Ergebnis\[p_{\rm B} = {\rm Q} \left( \frac{s_0}{\sigma_d}\right)\hspace{0.4cm}{\rm mit}\hspace{0.4cm}\rm Q (\it x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u \hspace{0.05cm}.\]
• Häufig – insbesondere in der englischsprachigen Literatur – wird anstelle der Funktion Q(x) die vergleichbare komplementäre Error Function erfc(x) verwendet. Mit dieser gilt:\[p_{\rm B} = {1}/{2} \cdot {\rm erfc} \left( \frac{s_0}{\sqrt{2}\cdot \sigma_d}\right)\hspace{0.4cm}{\rm mit}\hspace{0.4cm} {\rm erfc} (\it x) = \frac{\rm 2}{\sqrt{\rm \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u \hspace{0.05cm}.\]

Beide Funktionen findet man in Formelsammlungen in tabellarischer Form. Nachfolgend finden Sie ein Interaktionsmodul zur Berechnung der Funktionswerte von Q(x) und 1/2 · erfc(x):
Komplementäre Gaußsche Fehlerfunktionen
Zur Auswertung obiger Gleichungen ist nach Ansicht des Autors bei der Basisbandübertragung die Q–Funktion besser geeignet. Aber das ist natürlich Geschmacksache.

: Für das Folgende wird vorausgesetzt, dass Tabellen zur Verfügung stehen, in denen das Argument der Gaußschen Fehlerfunktionen im Abstand 0.1 aufgelistet sind.

Mit s₀/σ_d = 4 erhält man für die Bitfehlerwahrscheinlichkeit: \[p_{\rm B} = {\rm Q} (4) = 0.317 \cdot 10^{-4}\hspace{0.05cm},\] \[p_{\rm B} = {1}/{2} \cdot {\rm erfc} ( {4}/{\sqrt{2}})= {1}/{2} \cdot {\rm erfc} ( 2.828)\approx {1}/{2} \cdot {\rm erfc} ( 2.8)= 0.375 \cdot 10^{-4}\hspace{0.05cm}.\] Richtig ist der erste Wert. Bei der zweiten Berechnungsart muss man runden oder – noch besser – interpolieren, was aufgrund der starken Nichtlinearität dieser Funktion sehr schwierig ist.
Außerhalb von Übungsbeispielen wird s₀/σ_d in der Regel einen „krummen” Wert besitzen. In diesem Fall bietet „Q(x)” natürlich keinen Vorteil gegenüber „erfc(x)”.

Optimaler Binärempfänger - Realisierung mit Matched-Filter

Für das Folgende wird von den im Kapitel 1.1 genannten Voraussetzungen ausgegangen. Dann kann man für den Frequenzgang und die Impulsantwort des Empfängerfilters ansetzen:\[H_{\rm E}(f) = {\rm si}(\pi f T) \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} h_{\rm E}(t) = \left\{ \begin{array}{c} 1/T \\ 1/(2T) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} |\hspace{0.05cm}t\hspace{0.05cm}|< T/2 \hspace{0.05cm},\\ |\hspace{0.05cm}t\hspace{0.05cm}|= T/2 \hspace{0.05cm},\\ |\hspace{0.05cm}t\hspace{0.05cm}|>T/2 \hspace{0.05cm}. 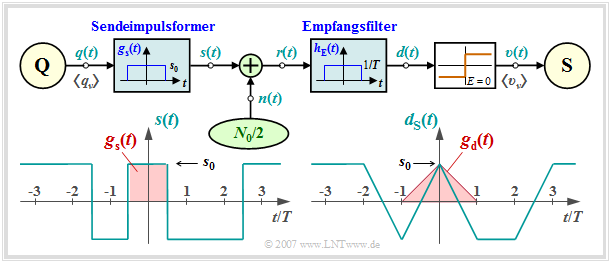\\ \end{array}\] Aufgrund der Linearität kann für das Detektionsnutzsignal geschrieben werden:\[d_{\rm S}(t) = \sum_{(\nu)} a_\nu \cdot g_d ( t - \nu \cdot T)\hspace{0.4cm}{\rm mit}\hspace{0.4cm}g_d(t) = g_s(t) \star h_{\rm E}(t) \hspace{0.05cm}.\] Die Faltung zweier Rechtecke gleicher Breite T ergibt einen dreieckförmigen Detektionsgrundimpuls g_d(t) mit g_d(t = 0) = s₀. Wegen g_d(|t| ≥ T) = 0 ist das System impulsinterferenzfrei; es gilt d_S(νT) = ±s₀.



Die Varianz des Detektionsstörsignals d_N(t) – also die Detektionsstörleistung – lautet:\[\sigma _d ^2 = \frac{N_0 }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H_{\rm E}( f )} \right|^2 \hspace{0.1cm}{\rm{d}}f} = \frac{N_0 }{2} \cdot \int_{- \infty }^{+ \infty } {\rm si}^2(\pi f T)\hspace{0.1cm}{\rm{d}}f = \frac{N_0 }{2T} \hspace{0.05cm}.\] Damit ergeben sich für die Bitfehlerwahrscheinlichkeit folgende Gleichungen:\[p_{\rm B} = {\rm Q} \left( \sqrt{\frac{2 \cdot s_0^2 \cdot T}{N_0}}\right)= {\rm Q} \left( \sqrt{\rho_d}\right)\hspace{0.05cm},\] \[p_{\rm B} = {1}/{2} \cdot {\rm erfc} \left( \sqrt{{ s_0^2 \cdot T}/{N_0}}\right)= {1}/{2}\cdot {\rm erfc}\left( \sqrt{{\rho_d}/{2}}\right) \hspace{0.05cm}.\] ρ_d ist das momentane Signal–zu–Stör–Leistungsverhältnis (SNR) des Detektionssignals d(t) zu den Zeitpunkten νT. Wir nennen es im Folgenden kurz „Detektions–SNR”. Es gilt die Definition\[\rho_d = \frac{d_{\rm S}^2(\nu T)}{{\rm E}[d_{\rm N}^2(\nu T)]}= \frac{s_0^2}{\sigma _d ^2} \hspace{0.05cm}.\]

Optimaler Binärempfänger - Realisierung mit Matched-Filter (2)

Ein Vergleich der Ergebnisse der letzten Seite mit Kapitel 5.4 von Buch „Stochastische Signaltheorie” zeigt, dass das Empfangsfilter H_E(f) ein an den Sendegrundimpuls g_s(t) angepasstes Matched–Filter ist:\[H_{\rm E}(f) = H_{\rm MF}(f) = K_{\rm MF}\cdot G_s^*(f)\hspace{0.05cm}.\]



Gegenüber der Seite Matched–Filter–Optimierung sind hier folgende Modifikationen berücksichtigt:

• Die Matched–Filter–Konstante ist hier zu K_MF = 1/(s₀ · T) gesetzt. Damit ist der Frequenzgang H_MF(f) dimensionslos.
• Der im allgemeinen frei wählbare Detektionszeitpunkt ist hier zu T_D = 0 gewählt. Damit ergibt sich allerdings ein akausales Filter.
• Das Detektions–SNR kann für jeden beliebigen Sendegrundimpuls g_s(t) mit Spektrum G_s(f) wie folgt dargestellt werden, wobei sich die rechte Identität aus dem Parsevalschen Theorem ergibt:\[\rho_d = \frac{2 \cdot E_{\rm B}}{N_0}\hspace{0.4cm}{\rm mit}\hspace{0.4cm} E_{\rm B} = \int^{+\infty} _{-\infty} g_s^2(t)\,{\rm d}t = \int^{+\infty} _{-\infty} |G_s(f)|^2\,{\rm d}f\hspace{0.05cm}.\]
• E_B wird oft als Energie pro Bit bezeichnet und E_B/N₀ – fälschlicherweise – als SNR. Bei binärer Basisbandübertragung unterscheidet sich E_B/N₀ vom tatsächlichen SNR ρ_d um den Faktor 2.
• Die auf der letzten Seite hergeleitete Bitfehlerwahrscheinlichkeit kann somit auch in der folgenden Weise geschrieben werden:\[p_{\rm B} = {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right)= {1}/{2} \cdot{\rm erfc} \left( \sqrt{{E_{\rm B}}/{N_0}}\right) \hspace{0.05cm}.\]

Die Eigenschaften des Matched-Filters werden in folgendem Interaktionsmodul behandelt: Zur Verdeutlichung des Matched-Filters.

Optimaler Binärempfänger – Realisierungsform „Integrate & Dump”

Bei rechteckförmigen NRZ–Sendeimpulsen kann das Matched–Filter auch als Integrator (jeweils über eine Symboldauer T) realisiert werden. Damit gilt für das Detektionssignal zu den Detektionszeitpunkten:\[d(\nu \cdot T + T/2) = \frac {1}{T} \cdot \int^{\nu \cdot T + T/2} _{\nu \cdot T - T/2} r(t)\,{\rm d}t \hspace{0.05cm}.\] Die folgende Grafik verdeutlicht die Unterschiede bei der Realisierung des optimalen Binärempfängers mit Matched–Filter (MF)  ⇒  mittlere Skizze bzw. als „Integrate & Dump” (I&D)  ⇒  untere Skizze.



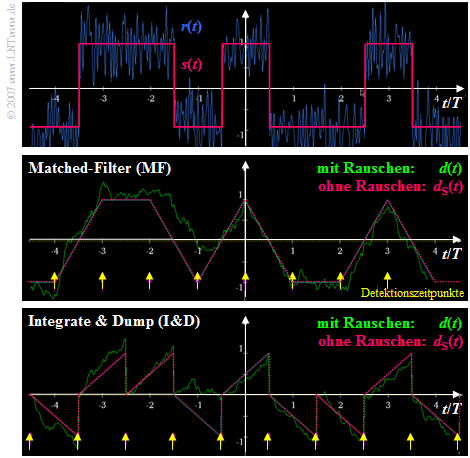
Man erkennt aus diesen Signalverläufen:

• Das Detektionsnutzsignal d_S(t) ist zu den Detektionszeitpunkten in beiden Fällen gleich ±s₀.
• Die unterschiedlichen Detektionszeitpunkte sind darauf zurückzuführen, dass das Matched–Filter im Gegensatz zu „Integrate & Dump” als akausal angesetzt wurde (siehe letzte Seite).
• Beim MF–Empfänger ist die Varianz des Detektionsstörsignals zu allen Zeiten t gleich:\[{\rm E}[d_{\rm N}^2(t)]= {\sigma _d ^2} = {\rm const.}\]

Dagegen nimmt beim I&D–Empfänger die Varianz von Symbolanfang bis Symbolende zu.

• Zu den Detektionszeitpunkten νT ist die Detektionsstörleistung in beiden Fällen gleich, so dass sich die genau gleiche Bitfehlerwahrscheinlichkeit ergibt. Mit E_B = s₀² · T gilt nämlich:\[\sigma _d ^2 = \frac{N_0}{2} \cdot \int_{- \infty }^{ +\infty } {\rm si}^2(\pi f T)\hspace{0.1cm}{\rm{d}}f = \frac{N_0}{2T} \hspace{0.05cm}\hspace{0.2cm} \Rightarrow \hspace{0.2cm} p_{\rm B} = {\rm Q} \left( \sqrt{ s_0^2 / \sigma _d ^2} \right)= {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right) \hspace{0.05cm}.\]

Interpretation des optimalen Empfängers

In diesem Abschnitt wurde gezeigt, dass mit einem Empfänger, bestehend aus linearem Empfangsfilter und nichtlinearem Entscheider, die kleinstmögliche Bitfehlerwahrscheinlichkeit zu erreichen ist:\[ p_{\rm B, \hspace{0.05cm}min} = {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right) = {1}/{2} \cdot {\rm erfc} \left( \sqrt{{ E_{\rm B}}/{N_0}}\right) \hspace{0.05cm}.\] Die sich ergebende Konfiguration ist ein Sonderfall des sog. Maximum–Aposteriori–Empfängers (MAP), der im Kapitel 3.7 dieses Buches behandelt wird. Für die Gültigkeit obiger Gleichung müssen allerdings eine Reihe von Voraussetzungen erfüllt sein::

• Das Sendesignal s(t) ist binär sowie bipolar (antipodisch) und weist pro Bit die (mittlere) Energie E_B auf. Die (mittlere) Sendeleistung ist somit E_B/T.
• Es liegt ein AWGN–Kanal (Additive White Gaussian Noise) mit der konstanten (einseitigen) Rauschleistungsdichte N₀ vor.
• Das Empfangsfilter H_E(f) ist bestmöglich an das Sendegrundimpulsspektrum G_s(f) entsprechend dem Matched–Filter–Kriterium angepasst.
• Der Entscheider (Schwellenwert, Detektionszeitpunkte) sei optimal. Eine kausale Realisierung des Matched–Filters kann man durch Verschiebung des Detektionszeitpunktes ausgleichen.
• Obige Gleichung gilt unabhängig vom Sendegrundimpuls g_s(t). Allein die für die Übertragung eines Binärsymbols aufgewendete Energie E_B ist entscheidend für die Fehlerwahrscheinlichkeit.
• Voraussetzung für die Anwendbarkeit obiger Gleichung ist, dass die Detektion eines Symbols nicht durch andere Symbole beeinträchtigt wird. Solche Impulsinterferenzen vergrößern p_B enorm.
• Ist die absolute Sendeimpulsdauer T_S kleiner oder gleich dem Symbolabstand T, so ist obige Gleichung bei Erfüllung des Matched-Filter-Kriteriums immer anwendbar.
• Die Gleichung gilt auch für Nyquistsysteme, bei denen zwar T_S > T gilt, es aber aufgrund von äquidistanten Nulldurchgängen des Grundimpulses g_d(t) nicht zu Impulsinterferenzen kommt.

Aufgaben

A1.2 Bitfehlerquote (BER)

A1.3 Einfluss von g(s) von (t) und h(E) von (t)