Exercise 3.7Z: Spread Spectrum in UMTS

Source signal and spread signal

For UMTS/CDMA, the so-called "PN modulation" is applied:

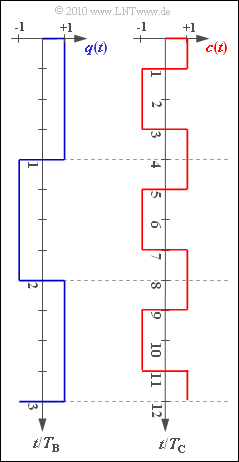
The rectangular digital signal $q(t)$ is multiplied by the spread signal $c(t)$ and gives the transmission signal $s(t)$.
This is by the spreading factor $J$ of higher frequency than $q(t)$; this is called "band spreading".

At the receiver the same spreading signal $c(t)$ is added (namely in phase!). This reverses the band spreading ⇒ "band compression".

The graphic shows exemplary signal characteristics of $q(t)$ und $c(t)$.

Notes:

This task refers to the chapter Characteristics of UMTS.
Reference is made to the chapter Telecommunications Aspects of UMTS in the book "Examples of Communication_Systems".
For the calculation of the chip duration $T_{\rm C}$, please refer to section Physical Channels .
There you will find, among other things, the information important for this task, which is transmitted on the so-called "Dedicated Physical Channel" $\rm (DPCH)$ in ten milliseconds exactly $15 \cdot 2560 \ \rm Chips$.
In subtask (5), the system asks for "transmitting chips".
For example, the "transmitting chip" $s_{3}$ denotes the constant signal value of $s(t)$ in the time interval $2T_{\rm C}$ ... $3T_{\rm C}$.

	For UMTS the bit duration $T_{\rm B}$ is fixed.
	For UMTS, the chip duration $T_{\rm C}$ is fixed.
	Both values depend on the channel conditions.

$R_{\rm C} \ = \ $

$\ \rm Mchip/s $

$T_{\rm C} \hspace{0.18cm} = \ $

$ \ \rm µ s $

$J \ = \ $

$R_{\rm B} \ = \ $

$\ \rm kbit/s $

$s_{3} \ = \ $

$s_{4} \ = \ $

$s_{5} \ = \ $

$s_{6} \ = \ $

(1) Correct is the solution 2:

For UMTS, the chip duration $T_{\rm C}$, which is still to be calculated in the subtask (2), is predefined.
The greater the degree of spreading $J$, the greater the bit duration.

(2) According to the note in the information section, in $10 \ \rm ms$ exactly $15 \cdot 2560 = 38400 \ \rm chips$ are transferred.

With this the chip rate: $R_{\rm C} = 100 \cdot 38400 \ {\rm Chips/s} \ \underline{= 3.84 \ \rm Mchip/s}$.
The chip duration is the reciprocal of this: $T_{\rm C} \ \underline{\approx 0.26 \ \rm µ s}$.

(3) Each data bit consists of four spreading chips ⇒ $\underline{J = 4}$.

(4) The bit rate is calculated with the spreading factor $J = 4$ to $R_{\rm B} = R_{\rm C}/J \ \underline{= 960 \ \rm kbit/s}$.

With the maximum spreading factor $J = 512$ for UMTS, the bit rate is only $7.5 \ \rm kbit/s$.

(5) The following applies to the transmission signal $s(t) = q(t) \cdot c(t)$.

The chips $s_{3}$ and $s_{4}$ of the transmission signal belong to the first data bit $(q_{1} = +1)$:

$$s_3 = c_3 \hspace{0.15cm}\underline {= -1},\hspace{0.4cm}s_4 = c_4 \hspace{0.15cm}\underline {= +1}\hspace{0.05cm}.$$

On the other hand, the two other transmission chips sought are to be assigned to the second data bit $(q_{2} = -1)$:

$$s_5 = -c_5= -c_1 \hspace{0.15cm}\underline {= -1},\hspace{0.4cm}s_6 = -c_6= -c_2 \hspace{0.15cm}\underline {= +1}\hspace{0.05cm}.$$