Eigenschaften nichtlinearer Systeme
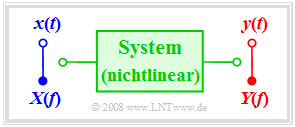
Wir gehen in diesem Abschnitt von folgender Konstellation aus:
Die Systembeschreibung mittels des Frequenzgangs $H(f)$ und/oder der Impulsantwort $h(t)$ ist nur bei einem LZI–System möglich. Beinhaltet aber das System auch nichtlineare Komponenten, so sind kein Frequenzgang und auch keine Impulsantwort angebbar und ein Beobachter wird Folgendes feststellen:
- Die Übertragungseigenschaften sind nun auch von der Größe des Eingangssignals abhängig. Führt $x(t)$ zum Ausgangssignal $y(t)$, so kann daraus nun nicht mehr geschlossen werden, dass sich beim Eingangssignal $K · x(t)$ stets das Signal $K · y(t)$ ergeben wird.
- Das bedeutet gleichzeitig, dass das Superpositionsprinzip nicht mehr anwendbar ist. Das bedeutet, dass aus den beiden Korrespondenzen $x_1(t)$ ⇒ $y_1(t)$ und $x_2(t)$ ⇒ $y_2(t)$ nicht auf das Übertragungsverhalten $x_1(t)$ + $x_2(t)$ ⇒ $y_1(t)$ + $y_2(t)$ geschlossen werden kann.
- Durch Nichtlinearitäten entstehen neue Frequenzen. Ist $x(t)$ eine harmonische Schwingung mit der Frequenz $f_0$, so beinhaltet das Ausgangssignal $y(t)$ auch Anteile bei Vielfachen von $f_0$. Diese bezeichnet man in der Nachrichtentechnik als Oberwellen.
- Ein Nachrichtensignal beinhaltet in der Praxis meist sehr viele Frequenzanteile. Die Oberwellen der niederfrequenten Signalanteile fallen nun in den Bereich höherfrequenter Nutzanteile. Dadurch ergeben sich nichtreversible Signalverfälschungen.
Bevor am Ende der Seite dieses Abschnitts Beispiele für das Auftreten nichtlinearer Verzerrungen in der Praxis genannt werden, soll das Problem der nichtlinearen Verzerrungen mathematisch erfasst werden. Wir setzen dabei voraus, dass das System kein Gedächtnis besitzt, so dass der Ausgangswert $y$ = $y(t_0)$ nur vom momentanen Eingangswert $x$ = $x(t_0)$ abhängt, nicht aber vom Signalverlauf $x(t)$ für $t$ < $t_0$.
Beschreibung nichtlinearer Systeme (1)
Definition: Ein System bezeichnet man als nichtlinear, wenn zu allen Zeiten zwischen dem Signalwert $x$ = $x(t)$ am Eingang und dem Ausgangssignalwert $y$ = $y(t)$ der folgende Zusammenhang besteht: $$y = g(x) \ne {\rm const.} \cdot x.$$ Man bezeichnet den Verlauf $y$ = $g(x)$ als die nichtlineare Kennlinie des Systems.
In der Grafik ist beispielhaft in grün die nichtlineare Kennlinie $y$ = $g(x)$ zu erkennen, die entsprechend dem ersten Viertel einer Sinusfunktion geformt ist. In roter Farbe gestrichelt erkennt man den Sonderfall eines linearen Systems mit der Kennlinie $y$ = $x$.