Exercise 4.08Z: Error Probability with Three Symbols

• Return to book

Decision regions with  $M = 3$

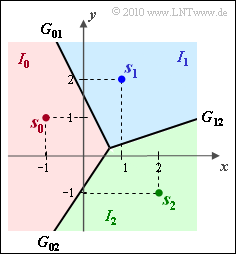
The diagram shows exactly the same signal space constellation as in  "Exercise 4.8":

• the  $M = 3$  possible transmitted signals,  viz.

$$\boldsymbol{ s }_0 = (-1, \hspace{0.1cm}1)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_1 = (1, \hspace{0.1cm}2)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_2 = (2, \hspace{0.1cm}-1)\hspace{0.05cm}.$$

• the  $M = 3$  decision boundaries

$$G_{01}\text{:} \hspace{0.4cm} y \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1.5 - 2 \cdot x\hspace{0.05cm},$$

$$G_{02}\text{:} \hspace{0.4cm} y \hspace{-0.1cm} \ = \ \hspace{-0.1cm} -0.75 +1.5 \cdot x\hspace{0.05cm},$$

$$G_{12}\text{:} \hspace{0.4cm} y \hspace{-0.1cm} \ = \ \hspace{-0.1cm} x/3\hspace{0.05cm}.$$

The two axes of the two-dimensional signal space are simplistically denoted here as  $x$  and  $y$;  actually,   $\varphi_1(t)/\sqrt {E}$  and  $\varphi_2(t)/\sqrt {E}$  should be written for these, respectively.

These decision boundaries are optimal under the two conditions:

• equal probability symbol probabilities,

• circularly–symmetric PDF of the noise  (e.g. AWGN).

In contrast,  in this exercise we consider a two–dimensional uniform distribution for the noise PDF:

$$\boldsymbol{ p }_{\boldsymbol{ n }} (x,\hspace{0.15cm} y) = \left\{ \begin{array}{c} K\\ 0 \end{array} \right.\quad \begin{array}{*{1}c}{\rm for} \hspace{0.15cm}|x| <A, \hspace{0.15cm} |y| <A \hspace{0.05cm}, \\ {\rm else} \hspace{0.05cm}.\\ \end{array}$$

• Such an amplitude-limited noise is admittedly without any practical meaning.

• However,  it allows an error probability calculation without extensive integrals,  from which the principle of the procedure can be seen.

Notes:

• The exercise belongs to the chapter  "Approximation of the Error Probability".

• To simplify the notation, the following is used:

$$x = {\varphi_1(t)}/{\sqrt{E}}\hspace{0.05cm}, \hspace{0.2cm} y = {\varphi_2(t)}/{\sqrt{E}}\hspace{0.05cm}.$$

Questions

1

What is the value of the constant  $K$  for  $A = 0.75$?

$\boldsymbol{K} \ = \ $

2

What is the symbol error probability with  $A = 0.75$?

$p_{\rm S} \ = \ $ $\ \%$

3

Which statements are true for  $A = 1$? 

	All messages  $m_i$  are falsified in the same way.
	Conditional error probability  ${\rm Pr(Fehler} \hspace{0.05cm} | \hspace{0.05cm} {\it m}_0) = 1/64$.
	Conditional error probability  ${\rm Pr(Fehler} \hspace{0.05cm} | \hspace{0.05cm} {\it m}_1) = 0$.
	Conditional error probability  ${\rm Pr(Fehler} \hspace{0.05cm} | \hspace{0.05cm} {\it m}_2) = 0$.

4

What is the error probability with  $A=1$  and  ${\rm Pr}(m_0) = {\rm Pr}(m_1) = {\rm Pr}(m_2) = 1/3$?

$p_{\rm S} \ = \ $ $\ \%$

5

What is the error probability with  $A=1$  and  ${\rm Pr}(m_0) = {\rm Pr}(m_1) = 1/4$  and  ${\rm Pr}(m_2) = 1/2$?

$p_{\rm S} \ = \ $ $\ \%$

6

Could a better result be obtained by specifying other regions?

	Yes.
	No.

Solution

Solution

Noise regions with $A = 0.75$

(1)  The volume of the 2D PDF must give $p_n(x, y) =1$, that is:

$$2A \cdot 2A \cdot K = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} K = \frac{1}{4A^2}\hspace{0.05cm}.$$

• With $A = 0.75$   ⇒   $2A = 3/2$, we get $K = 4/9 \ \underline {=0.444}$.

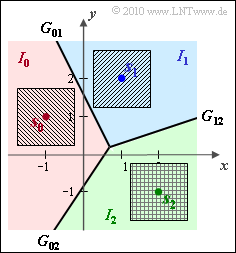
(2)  In the accompanying graph, the noise component $\boldsymbol{n}$ is plotted by the squares of edge length $1.5$ around the 2D signal space points $\boldsymbol{s}_i$.

• It can be seen that no decision boundary is exceeded by noise components.
• It follows:  The symbol error probability is $p_{\rm S}\ \underline { \equiv 0}$ under the conditions given here.

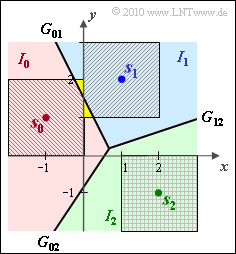
(3)  Statements 2 and 4 are correct, as can be seen from the graph below:

• The message $m_2$ cannot be falsified because the square around $\boldsymbol{s}_2$ lies entirely in the lower right quadrant and thus in the decision area $I_2$.
• Likewise, $m_2$ was sent with certainty if the received value lies in decision area $I_2$.
  The reason: none of the squares around $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$ extends into the area $I_2$.
• $m_0$ can only be falsified to $m_1$. The (conditional) falsification probability is equal to the ratio of the areas of the yellow triangle (area $1/16$) and the square (area 4):

Noise regions with A = 1

$${\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_0 ) = \frac{1/2 \cdot 1/2 \cdot 1/4}{4}= {1}/{64} \hspace{0.05cm}.$$

• For symmetry reasons, equally:

$${\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_1 ) = {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_0 )={1}/{64} \hspace{0.05cm}.$$

(4)  For equal probability symbols, we obtain for the (average) error probability:

$$p_{\rm S} = {\rm Pr}({ \cal E} ) = {1}/{3} \cdot \big [{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_0 ) + {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_1 )+{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_2 )\big ]$$

$$\Rightarrow \hspace{0.3cm} p_{\rm S} = {\rm Pr}({ \cal E} ) = {1}/{3} \cdot \left [{1}/{64} + {1}/{64} + 0 )\right ]= \frac{2}{3 \cdot 64} = {1}/{96}\hspace{0.1cm}\hspace{0.15cm}\underline {\approx 1.04 \%} \hspace{0.05cm}.$$

(5)  Now we obtain a smaller average error probability, viz.

$$p_{\rm S} = {\rm Pr}({ \cal E} ) = {1}/{4} \cdot {1}/{64} + {1}/{4} \cdot {1}/{64}+ {1}/{2} \cdot0 = {1}/{128}\hspace{0.1cm}\hspace{0.15cm}\underline {\approx 0.78 \% } \hspace{0.05cm}.$$

(6)  Correct is YES:

• For example,     $I_1$: first quadrant,     $I_0$: second quadrant,     $I_2 \text{:} \ y < 0$     would give zero error probability.
• This means that the given bounds are optimal only in the case of circularly symmetric PDF of the noise, for example, the AWGN channel.