Contents
- 1 # ÜBERBLICK ZUM ERSTEN HAUPTKAPITEL #
- 2 Fehlererkennung und Fehlerkorrektur
- 3 Einige einführende Beispiele zur Fehlererkennung
- 4 Einige einführende Beispiele zur Fehlerkorrektur
- 5 Die „Geschlitzte CD” – eine Demonstration des LNT der TUM
- 6 Zusammenspiel zwischen Quellen– und Kanalcodierung
- 7 Blockschaltbild und Voraussetzungen
- 8 Einige wichtige Definitionen zur Blockcodierung
- 9 Beispiele für Fehlererkennung und Fehlerkorrektur
- 10 Zur Nomenklatur in diesem Buch
- 11 Aufgaben zum Kapitel
- 12 Quellenverzeichnis
# ÜBERBLICK ZUM ERSTEN HAUPTKAPITEL #
Das erste Kapitel behandelt Blockcodes zur Fehlererkennung und Fehlerkorrektur und liefert die Grundlagen zur Beschreibung effektiverer Codes wie zum Beispiel den Reed–Solomon–Codes (siehe Kapitel 2), den Faltungscodes (Kapitel 3) sowie den iterativ decodierbaren Produkt–Codes (Turbo–Codes) und Low–density Parity–check Codes (Kapitel 4). Wir beschränken uns hier auf binäre Codes.
Man bezeichnet dieses spezifische Fachgebiet als Kanalcodierung im Gegensatz zur Quellencodierung (Redundanzminderung aus Gründen der Datenkomprimierung) und zur Leitungscodierung (zusätzliche Redundanz zur Anpassung des Digitalsignals an die spektralen Eigenschaften des Übertragungsmediums).
Im Einzelnen werden behandelt:
- Definitionen und einführende Beispiele zur Fehlererkennung und Fehlererkorrektur,
- eine kurze Wiederholung geeigneter Kanalmodelle und Entscheiderstrukturen,
- bekannte binäre Blockcodes wie Single Parity-check Code, Wiederholungscode und Hamming–Code,
- die allgemeine Beschreibung linearer Codes mittels Generatormatrix und Prüfmatrix,
- die Decodiermöglichkeiten für Blockcodes, unter anderem die Syndromdecodierung,
- einfache Näherungen und obere Schranken für die Blockfehlerwahrscheinlichkeit, sowie
- eine informationstheoretische Grenze der Kanalcodierung.
Fehlererkennung und Fehlerkorrektur
Bei einem jeden Nachrichtenübertragungssystem kommt es zu Übertragungsfehlern. Man kann zwar die Wahrscheinlichkeit $p_{\rm S}$ für einen solchen Symbolfehler sehr klein halten, zum Beispiel durch eine sehr große Signalenergie. Die Symbolfehlerwahrscheinlichkeit $p_{\rm S} = 0$ ist aber wegen der Gaußschen WDF des stets vorhandenen thermischen Rauschens nie erreichbar.
Insbesondere bei stark gestörten Kanälen und auch für sicherheitskritische Anwendungen ist es deshalb unumgänglich, die zu übertragenden Daten angepasst an Anwendung und Kanal besonders zu schützen. Dazu fügt man beim Sender Redundanz hinzu und nutzt diese Redundanz beim Empfänger, um die Anzahl der Decodierfehler zu verringern.
$\text{Definitionen:}$
- Fehlererkennung (englisch: Error Detection): Der Decoder prüft die Integrität der empfangenen Blöcke und markiert gefundene Fehler. Eventuell informiert der Empfänger den Sender über fehlerhafte Blöcke via Rückkanal, so dass dieser den entsprechenden Block noch einmal sendet.
- Fehlerkorrektur (englisch: Error Correction): Der Decoder erkennt einen (oder mehrere) Bitfehler und liefert für diese weitere Informationen, zum Beispiel deren Positionen im übertragenen Block. Damit können unter Umständen die entstandenen Fehler vollständig korrigiert werden.
- Die Kanalcodierung (englisch: Channel Coding oder Error–Control Coding) umfasst sowohl Verfahren zur Fehlererkennung als auch solche zur Fehlerkorrektur.
Alle ARQ–Verfahren (englisch: Automatic Repeat Request ) nutzen ausschließlich Fehlererkennung. Für die Fehlererkennung ist weniger Redundanz erforderlich als für eine Fehlerkorrektur. Ein Nachteil der ARQ ist der geringe Durchsatz bei schlechter Kanalqualität, also dann, wenn häufig ganze Datenblöcke vom Empfänger neu angefordert werden müssen.
In diesem Buch behandeln wir größtenteils die Vorwärtsfehlerkorrektur (englisch: Forward Error Correction, FEC), die bei einem ausreichend guten Kanal (großes SNR) zu sehr kleinen Fehlerraten führt. Bei schlechteren Kanalbedingungen ändert sich am Durchsatz nichts, das heißt, es wird die gleiche Informationsmenge übertragen. Allerdings kann dann die Fehlerrate sehr große Werte annehmen.
Oft werden FEC– und ARQ–Verfahren kombiniert, und zwischen diesen die Redundanz so aufgeteilt,
- dass eine kleine Anzahl von Fehlern noch korrigierbar ist,
- bei vielen Fehlern aber eine Wiederholung des Blocks angefordert wird.
Einige einführende Beispiele zur Fehlererkennung
$\text{Beispiel 1: Single Parity–check Code (SPC)}$
Ergänzt man $k = 4$ Bit um ein so genanntes Prüfbit (englisch: Parity Bit ) derart, dass die Summe aller Einsen geradzahlig ist, zum Beispiel (mit fettgedruckten Prüfbits)
- $$0000\boldsymbol{0}, 0001\boldsymbol{1}, \text{...} , 1111\boldsymbol{0}, \text{...}\ ,$$
so kann man einen Einzelfehler sehr einfach erkennen. Zwei Fehler innerhalb eines Codewortes bleiben dagegen unerkannt.
Die deutsche Bezeichnung hierfür ist Paritätsprüfcode.
$\text{Beispiel 2: International Standard Book Number (ISBN)}$
Seit den 1960er Jahren werden alle Bücher mit 10–stelligen Kennzahlen (ISBN–10 ) versehen. Seit 2007 ist zusätzlich noch die Angabe gemäß ISBN–13 verpflichtend. Beispielsweise lauten diese für das Fachbuch [Söd93][1]:
- $\boldsymbol{3–540–57215–5}$ (für ISBN–10), bzw.
- $\boldsymbol{978–3–54057215–2}$ (für ISBN–13).
Die letzte Ziffer $z_{10}$ ergibt sich bei ISBN–10 aus den vorherigen Ziffern $z_1 = 3$, $z_2 = 5$, ... , $z_9 = 5$ nach folgender Rechenregel:
- \[z_{10} = \left ( \sum_{i=1}^{9} \hspace{0.2cm} i \cdot z_i \right ) \hspace{-0.3cm} \mod 11 = (1 \cdot 3 + 2 \cdot 5 + ... + 9 \cdot 5 ) \hspace{-0.2cm} \mod 11 = 5 \hspace{0.05cm}. \]
Zu beachten ist, dass $z_{10} = 10$ als $z_{10} = \rm X$ geschrieben werden muss (römische Zahlendarstellung von „10”), da sich die Zahl $10$ im Zehnersystem nicht als Ziffer darstellen lässt.
Entsprechend gilt für die Prüfziffer bei ISBN–13:
- \[z_{13}= 10 - \left ( \sum_{i=1}^{12} \hspace{0.2cm} z_i \cdot 3^{(i+1) \hspace{-0.2cm} \mod 2} \right ) \hspace{-0.3cm} \mod 10 = 10 \hspace{-0.05cm}- \hspace{-0.05cm} \big [(9\hspace{-0.05cm}+\hspace{-0.05cm}8\hspace{-0.05cm}+\hspace{-0.05cm}5\hspace{-0.05cm}+\hspace{-0.05cm}0\hspace{-0.05cm}+\hspace{-0.05cm}7\hspace{-0.05cm}+\hspace{-0.05cm}1) \cdot 1 + (7\hspace{-0.05cm}+\hspace{-0.05cm}3\hspace{-0.05cm}+\hspace{-0.05cm}4\hspace{-0.05cm}+\hspace{-0.05cm}5\hspace{-0.05cm}+\hspace{-0.05cm}2\hspace{-0.05cm}+\hspace{-0.05cm}5) \cdot 3\big ] \hspace{-0.2cm} \mod 10 \]
- \[\Rightarrow \hspace{0.3cm} z_{13}= 10 - (108 \hspace{-0.2cm} \mod 10) = 10 - 8 = 2 \hspace{0.05cm}. \]
Bei beiden Varianten werden im Gegensatz zum obigen Paritätsprüfcode (SPC) auch Zahlendreher wie $57 \, \leftrightarrow 75$ erkannt, da hier unterschiedliche Positionen verschieden gewichtet werden.
$\text{Beispiel 3: Strichcode (eindimensionaler Barcode)}$
Der am weitesten verbreitete fehlererkennende Code weltweit ist der Strichcode oder Balkencode (englisch: Bar Code) zur Kennzeichnung von Produkten, zum Beispiel nach EAN–13 (European Article Number ) mit 13 Ziffern.
- Diese werden durch verschieden breite Balken und Lücken dargestellt und können mit einem opto–elektronischen Lesegerät leicht entschlüsselt werden.
- Die ersten drei Ziffern kennzeichnen das Land (beispielsweise Deutschland: zwischen 400 und 440), die nächsten vier bzw. fünf Stellen den Hersteller und das Produkt.
- Die letzte Ziffer ist die Prüfziffer $z_{13}$, die sich genau so berechnet wie bei ISBN–13.
Einige einführende Beispiele zur Fehlerkorrektur
$\text{Beispiel 4: 2D–Barcodes für Online–Tickets}$
Wenn Sie eine Fahrkarte der Deutschen Bahn online buchen und ausdrucken, finden Sie ein Beispiel eines zweidimensionalen Barcodes, nämlich den 1995 von Andy Longacre bei der Firma Welch Allyn in den USA entwickelten Aztec–Code, mit dem Datenmengen bis zu $3000$ Zeichen codiert werden können. Aufgrund der Reed–Solomon–Fehlerkorrektur ist die Rekonstruktion des Dateninhalts auch dann noch möglich, wenn bis zu $40\%$ des Codes zerstört wurden, zum Beispiel durch Knicken der Fahrkarte oder durch Kaffeeflecken.
Rechts ist ein $\rm QR–Code$ (Quick Response) mit zugehörigem Inhalt dargestellt. Der QR–Code wurde 1994 für die Autoindustrie in Japan zur Kennzeichnung von Bauteilen entwickelt und erlaubt ebenfalls eine Fehlerkorrektur. Inzwischen ist der Einsatz des QR–Codes sehr vielfältig. In Japan findet man ihn auf nahezu jedem Werbeplakat und auf jeder Visitenkarte. Auch in Deutschland setzt er sich mehr und mehr durch.
Bei allen 2D–Barcodes gibt es quadratische Markierungen zur Kalibrierung des Lesegerätes. Details hierzu finden Sie in [KM+09][2].
$\text{Beispiel 5: Codes für die Satelliten– und Weltraumkommunikation}$
Eines der ersten Einsatzgebiete von Fehlerkorrekturverfahren war die Kommunikation von/zu Satelliten und Raumfähren, also Übertragungsstrecken, die durch niedrige Sendeleistungen und große Pfadverluste gekennzeichnet sind. Schon 1977 wurde bei der Raum–Mission Voyager 1 zu Neptun und Uranus Kanalcodierung eingesetzt, und zwar in Form der seriellen Verkettung eines Reed–Solomon–Codes und eines Faltungscodes.
Damit genügte schon der Leistungskennwert $10 · \lg \; E_{\rm B}/N_0 \approx 2 \, \rm dB$, um die geforderte Fehlerrate $5 · 10^{-5}$ (bezogen auf die komprimierten Daten nach der Quellencodierung) zu erreichen. Ohne Kanalcodierung sind dagegen für die gleiche Fehlerrate fast $9 \, \rm dB$ erforderlich, also eine um den Faktor $10^{0.7} ≈ 5$ größere Sendeleistung.
Auch das geplante Marsprojekt (die Datenübertragung vom Mars zur Erde mit $\rm 5W$–Lasern) wird nur mit einem ausgeklügelten Codierschema erfolgreich sein.
$\text{Beispiel 6: Kanalcodes für die Mobilkommunikation}$
Ein weiteres und besonders umsatzstarkes Anwendungsgebiet, das ohne Kanalcodierung nicht funktionieren würde, ist die Mobilkommunikation. Hier ergäben sich bei ungünstigen Bedingungen ohne Codierung Fehlerraten im Prozentbereich und aufgrund von Abschattungen und Mehrwegeausbreitung (Echos) treten die Fehler oft gebündelt auf. Die Fehlerbündellänge beträgt dabei manchmal einige Hundert Bit.
- Bei der Sprachübertragung im GSM–System werden die $182$ wichtigsten (Klasse 1a und 1b) der insgesamt 260 Bit eines Sprachrahmens $(20 \, \rm ms)$ zusammen mit einigen wenigen Paritäts– und Tailbits faltungscodiert $($mit Memory $m = 4$ und Rate $R = 1/2)$ und verwürfelt. Zusammen mit den $78$ weniger wichtigen und deshalb uncodierten Bits der Klasse 2 führt dies dazu, dass die Bitrate von $13 \, \rm kbit/s$ auf $22.4 \, \rm kbit/s$ ansteigt.
- Man nutzt die (relative) Redundanz von $r = (22.4 - 13)/22.4 ≈ 0.42$ zur Fehlerkorrektur. Anzumerken ist, dass $r = 0.42$ aufgrund der hier verwendeten Definition aussagt, das $42\%$ der codierten Bits redundant sind. Mit dem Bezugswert „Bitrate der uncodierten Folge” ergäbe sich $r = 9.4/13 \approx 0.72$ mit der Aussage: Zu den Informationsbits werden $72\%$ Prüfbits hinzugefügt.
- Bei UMTS (Universal Mobile Telecommunications System) werden Faltungscodes mit den Raten $R = 1/2$ bzw. $R = 1/3$ eingesetzt. Bei den UMTS–Modi für höhere Datenraten und entsprechend geringeren Spreizfaktoren verwendet man dagegen Turbo–Codes der Rate $R = 1/3$ und iterative Decodierung. Abhängig von der Anzahl der Iterationen erzielt man gegenüber der Faltungscodierung hiermit Gewinne von bis zu $3 \, \rm dB$.
$\text{Beispiel 7: Fehlerschutz der Compact Disc}$
Bei einer CD (Compact Disc) verwendet man einen cross–interleaved Reed–Solomon–Code (RS) und anschließend eine so genannte Eight–to–Fourteen–Modulation. Die Redundanz nutzt man zur Fehlererkennung und –korrektur. Dieses Codierschema zeigt folgende Charakteristika:
- Die gemeinsame Coderate der zwei RS–Komponentencodes beträgt $R_{\rm RS} = 24/28 · 28/32 = 3/4$. Durch die 8–to–14–Modulation und einiger Kontrollbits kommt man zur Gesamtcoderate $R ≈ 1/3$.
- Bei statistisch unabhängigen Fehlern gemäß dem BSC–Modell (Binary Symmetric Channel ) ist eine vollständige Korrektur möglich, so lange die Bitfehlerrate den Wert $10^{-3}$ nicht überschreitet.
- Der CD–spezifische Cross Interleaver verwürfelt $108$ Blöcke miteinander, so dass die $588$ Bit eines Blockes $($jedes Bit entspricht ca. $0.28 \, \rm {µ m})$ auf etwa $1.75\, \rm cm$ verteilt werden.
- Mit der Coderate $R ≈ 1/3$ kann man ca. $10\%$ „Erasures” korrigieren. Die verloren gegangenen Werte lassen sich durch Interpolation (näherungsweise) rekonstruieren ⇒ Fehlerverschleierung.
Zusammenfassend lässt sich sagen: Weist eine CD einen Kratzer von $1.75\, \rm mm$ Länge in Abspielrichtung auf (also mehr als $6000$ aufeinanderfolgende Erasures), so sind immer noch $90\%$ aller Bits eines Blockes fehlerfrei, so dass sich auch die fehlenden $10\%$ rekonstruieren lassen, oder dass die Auslöschungen zumindest so verschleiert werden können, dass sie nicht hörbar sind.
Auf der nächsten Seite folgt eine Demonstration zur Korrekturfähigkeit der CD.
Die „Geschlitzte CD” – eine Demonstration des LNT der TUM
Ende der 1990er Jahre haben Mitarbeiter des Lehrstuhls für Nachrichtentechnik der TU München unter Leitung von Professor Joachim Hagenauer eine Musik–CD gezielt beschädigt, indem insgesamt drei Schlitze von jeweils mehr als einem Millimeter Breite eingefräst wurden. Damit fehlen bei jedem Defekt fast $4000$ fortlaufende Bit der Audiocodierung.
Die Grafik zeigt die „geschlitzte CD”:
- Sowohl in der Spur 3 als auch in der Spur 14 gibt es bei jeder Umdrehung zwei solcher fehlerhafter Bereiche.
- Sie können sich die Musikqualität mit Hilfe der beiden Audioplayer (Abspielzeit jeweils ca. 15 Sekunden) verdeutlichen.
- Die Theorie zu dieser Audio–Demo finden Sie im $\text{Beispiel 7}$ auf der vorherigen Seite.
Spur 14:
Spur 3:
Resumee dieser Audiodemo:
- Die Fehlerkorrektur der CD basiert auf zwei seriell–verketteten Reed–Solomon–Codes sowie einer Eight–to–Fourteen–Modulation. Die Gesamtcoderate zur RS–Fehlerkorrektur beträgt $R = 3/4$.
- Ebenso wichtig für die Funktionsfähigkeit der CD wie die Codes ist der dazwischen geschaltete Interleaver, der die ausgelöschten Bits („Erasures”) über eine Länge von fast $2 \, \rm cm$ verteilt.
- Bei der Spur 14 liegen die beiden defekten Bereiche genügend weit auseinander. Deshalb ist der Reed–Solomon–Decoder in der Lage, die fehlenden Daten zu rekonstruieren.
- Bei der Spur 3 folgen die beiden Fehlerblöcke in sehr kurzem Abstand aufeinander, so dass der Korrekturalgorithmus versagt. Das Resultat ist ein fast periodisches Klackgeräusch.
Wir bedanken uns bei Rainer Bauer, Thomas Hindelang und Manfred Jürgens, diese Audio–Demo verwenden zu dürfen.
Zusammenspiel zwischen Quellen– und Kanalcodierung
Die Nachrichtenübertragung natürlicher Quellen wie Sprache, Musik, Bilder, Videos, usw. geschieht meist entsprechend dem nachfolgend skizzierten zeitdiskreten Modell.
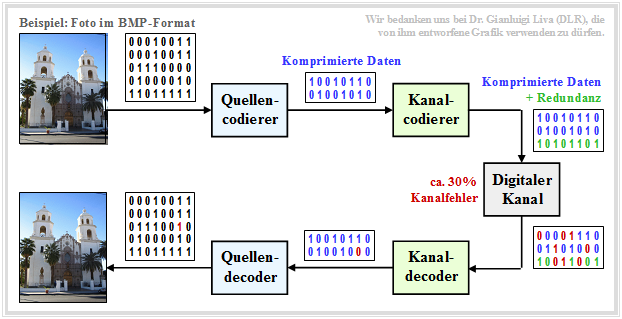
Zu dieser aus [Liv10][3] entnommenen Grafik ist Folgendes anzumerken:
- Quelle und Sinke sind digitalisiert und werden durch (etwa gleich viele ) Nullen und Einsen repräsentiert.
- Der Quellencodierer komprimiert die binären Daten – im Beispiel ein Digitalfoto – und reduziert somit die Redundanz der Quelle.
- Der Kanalcodierer fügt wieder Redundanz hinzu und zwar gezielt, so dass einige der auf dem Kanal entstandenen Fehler im Kanaldecoder korrigiert werden können.
- Für den Kanal wird hier ein zeitdiskretes Modell mit binärem Eingang und Ausgang verwendet, das auch die Komponenten der technischen Sende– und Empfangseinrichtungen (Modulator, Entscheider, Taktwiedergewinnung) geeignet berücksichtigen sollte.
Bei richtiger Dimensionierung von Quellen– und Kanalcodierung ist die Qualität des empfangenen Fotos hinreichend gut, auch wenn die Sinkensymbolfolge aufgrund nicht korrigierbarer Fehlermuster nicht exakt mit der Quellensymbolfolge übereinstimmen wird. Man erkennt innerhalb der Sinkensymbolfolge einen (rot markierten) Bitfehler.
$\text{Beispiel 8:}$ Für obige Grafik wurde beispielhaft und stark vereinfachend angenommen, dass
- die Quellensymbolfolge nur die Länge $40$ hat,
- der Quellencodierer die Daten um den Faktor $40/16 = 2.5$ komprimiert, und
- der Kanalcoder $50\%$ Redundanz hinzufügt.
Übertragen werden müssen also nur $24$ Codersymbole statt $40$ Quellensymbole, was die Übertragungsrate insgesamt um $40\%$ reduziert.
Würde man auf die Quellencodierung verzichten, in dem man das ursprüngliche Foto im BMP–Format übertragen würde und nicht das komprimierte JPG–Bild, so wäre die Qualität vergleichbar, aber eine um den Faktor $2.5$ höhere Bitrate und damit sehr viel mehr Aufwand erforderlich.
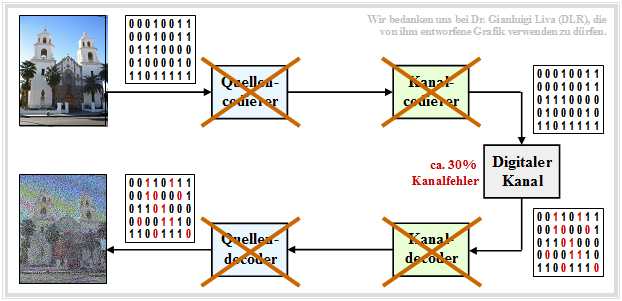
$\text{Beispiel 9:}$ Würde man sowohl auf die Quellen– als auch auf die Kanalcodierung verzichten, also direkt die BMP–Daten ohne Fehlerschutz übertragen, so wäre das Ergebnis trotz $($um den Faktor $40/24)$ größerer Bitrate äußerst dürftig.
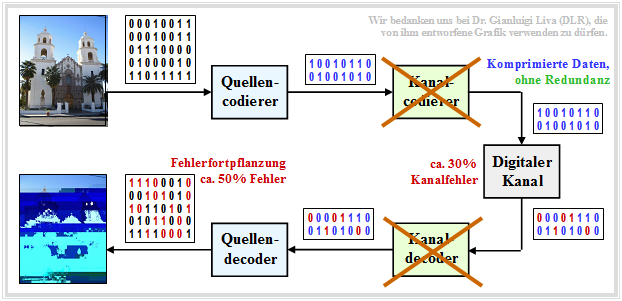
$\text{Beispiel 10:}$ Nun betrachten wir den Fall, dass man die komprimierten Daten (zum Beispiel JPG) ohne Fehlersicherungsmaßnahmen direkt überträgt.
- Da die komprimierte Quelle nur noch wenig Redundanz besitzt, führt jeder einzelne Übertragungsfehler dazu, dass ganze Bildblöcke falsch decodiert werden.
- Dieses Codierschema (Quellencodierung, aber keine Kanalcodierung) sollte auf jeden Fall vermieden werden.
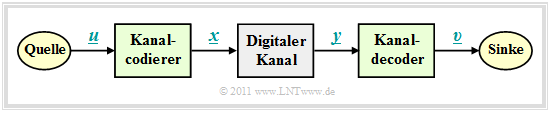
Blockschaltbild und Voraussetzungen
Im weiteren Verlauf gehen wir von dem skizzierten Blockschaltbild mit Kanalcodierer, Digitalem Kanal und Kanaldecoder aus.
Dabei gelten folgende Voraussetzungen:
- Der Vektor $\underline{u} = (u_1, u_2, \text{...} \hspace{0.05cm}, u_k)$ kennzeichnet einen Informationsblock mit $k$ Symbolen.
- Meist beschränken wir uns auf Binärsymbole (Bits) ⇒ $u_i \in \{0, \, 1\}$ für $i = 1, 2, \text{...} \hspace{0.05cm}, k$ mit gleichen Auftrittswahrscheinlichkeiten für Nullen und Einsen.
- Jeder Informationsblock $\underline{u}$ wird durch ein Codewort (oder einen Codeblock) $\underline{x} = (x_1, x_2, \text{...} \hspace{0.05cm}, x_n)$ mit $n \ge k$, $x_i \in \{0, \, 1\}$ dargestellt. Man spricht dann von einem binären $(n, k)$–Blockcode $C$. Die Zuordnung bezeichnen wir mit $\underline{x} = {\rm enc}(\underline{u})$, wobei „enc” für „Encoder–Funktion” steht.
- Das Empfangswort $\underline{y}$ ergibt sich aus dem Codewort $\underline{x}$ durch Modulo–2–Addition mit dem ebenfalls binären Fehlervektor $\underline{e} = (e_1, e_2, \text{...} \hspace{0.05cm}, e_n)$, wobei „$e= 1$” für einen Übertragungfehler steht und „$e= 0$” anzeigt, dass das $i$–te Bit des Codewortes richtig übertragen wurde. Es gilt also:
- \[\underline{y} = \underline{x} \oplus \underline{e} \hspace{0.05cm}, \hspace{0.5cm} y_i = x_i \oplus e_i \hspace{0.05cm}, \hspace{0.2cm} i = 1, \text{...} \hspace{0.05cm} , n\hspace{0.05cm}, x_i \hspace{-0.05cm} \in \hspace{-0.05cm} \{ 0, 1 \}\hspace{0.05cm}, \hspace{0.5cm}e_i \in \{ 0, 1 \}\hspace{0.5cm} \Rightarrow \hspace{0.5cm}y_i \in \{ 0, 1 \}\hspace{0.05cm}.\]
- Die Beschreibung durch das Digitale Kanalmodell – also mit binärem Eingang und Ausgang – ist allerdings nur dann anwendbar, wenn das Übertragungssystem harte Entscheidungen trifft – siehe AWGN–Kanal bei binärem Eingang. Systeme mit Soft Decision sind mit diesem einfachen Modell nicht modellierbar.
- Der Vektor $\underline{v}$ nach der Kanaldecodierung hat die gleiche Länge $k$ wie der Informationsblock $\underline{u}$. Den Decodiervorgang beschreiben wir mit der „Decoder–Funktion” als $\underline{v} = {\rm enc}^{-1}(\underline{y}) = {\rm dec}(\underline{y})$. Im fehlerfreien Fall gilt analog zu $\underline{x} = {\rm enc}(\underline{u})$ auch $\underline{v} = {\rm enc}^{-1}(\underline{y})$.
- Ist der Fehlervektor $\underline{e} \ne \underline{0}$, so ist $\underline{y}$ meist kein gültiges Element des verwendeten Blockcodes, und die Decodierung ist dann keine reine Zuordnung $\underline{y} \rightarrow \underline{v}$, sondern eine auf maximale Übereinstimmung (mimimale Fehlerwahrscheinlichkeit) basierende Schätzung von $\underline{v}$.
Einige wichtige Definitionen zur Blockcodierung
Wir betrachten nun den beispielhaften binären Blockcode
\[\mathcal{C} = \{ (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm} (0, 1, 0, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 0, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 1, 1) \}\hspace{0.05cm}.\]
Dieser Code wäre zum Zwecke der Fehlererkennung oder –korrektur ungeeignet. Aber er ist so konstruiert, dass er die Berechnung wichtiger Beschreibungsgrößen anschaulich verdeutlicht:
- Jedes einzelne Codewort $\underline{u}$ wird durch fünf Bit beschrieben. Im gesamten Buch drücken wir diesen Sachverhalt durch die Codewortlänge (englisch: Code Length ) $n = 5$ aus.
- Der obige Code beinhaltet vier Elemente. Damit ist der Codeumfang (englisch: Size ) $|C| = 4$. Entsprechend gibt es auch vier eindeutige Zuordnungen (englisch: Mappings ) zwischen $\underline{u}$ und $\underline{x}$.
- Die Länge eines Informationsblocks $\underline{u}$ ⇒ Informationsblocklänge wird mit $k$ bezeichnet. Da bei allen binären Codes $|C| = 2^k$ gilt, folgt aus $|C| = 4$ der Wert $k = 2$. Die Zuordnungen zwischen $\underline{u}$ und $\underline{x}$ lauten bei obigem Code $C$:
- \[\underline{u_0} = (0, 0) \hspace{0.2cm}\leftrightarrow \hspace{0.2cm}(0, 0, 0, 0, 0) = \underline{x_0}\hspace{0.05cm}, \hspace{0.8cm} \underline{u_1} = (0, 1) \hspace{0.2cm}\leftrightarrow \hspace{0.2cm}(0, 1, 0, 1, 0) = \underline{x_1}\hspace{0.05cm}, \]
- \[\underline{u_2} = (1, 0)\hspace{0.2cm} \leftrightarrow \hspace{0.2cm}(1, 0, 1, 0, 1) = \underline{x_2}\hspace{0.05cm}, \hspace{0.8cm} \underline{u_3} = (1, 1) \hspace{0.2cm} \leftrightarrow \hspace{0.2cm}(1, 1, 1, 1, 1) = \underline{x_3}\hspace{0.05cm}.\]
- Der Code weist die Coderate $R = k/n = 2/5$ auf. Dementsprechend beträgt seine Redundanz $1-R$, also $60\%$. Ohne Fehlerschutz $($also für den Fall $n = k)$ wäre die Coderate $R = 1$.
- Eine kleine Coderate zeigt an, dass von den $n$ Bits eines Codewortes nur sehr wenige tatsächlich Information tragen. Beispielsweise hat ein Wiederholungscode $(k = 1)$ mit $n = 10$ die Coderate $R = 0.1$.
- Das Hamming–Gewicht $w_{\rm H}(\underline{x})$ des Codewortes $\underline{x}$ gibt die Zahl der Codewortelemente $x_i \ne 0$ an. Bei einem binären Code ⇒ $x_i \in \{0, \, 1\}$ ist $w_{\rm H}(\underline{x})$ gleich der Summe $x_1 + x_2 + \hspace{0.05cm}\text{...} \hspace{0.05cm}+ x_n$. Im Beispiel:
- \[w_{\rm H}(\underline{x}_0) = 0\hspace{0.05cm}, \hspace{0.4cm}w_{\rm H}(\underline{x}_1) = 2\hspace{0.05cm}, \hspace{0.4cm} w_{\rm H}(\underline{x}_2) = 3\hspace{0.05cm}, \hspace{0.4cm}w_{\rm H}(\underline{x}_3) = 5\hspace{0.05cm}. \]
- Die Hamming–Distanz $d_{\rm H}(\underline{x}, \ \underline{x}\hspace{0.03cm}')$ zwischen den Codeworten $\underline{x}$ und $\underline{x}\hspace{0.03cm}'$ bezeichnet die Anzahl der Bitpositionen, in denen sich die beiden Codeworte unterscheiden:
- \[d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_1) = 2\hspace{0.05cm}, \hspace{0.4cm} d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_2) = 3\hspace{0.05cm}, \hspace{0.4cm} d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_3) = 5\hspace{0.05cm},\hspace{0.4cm} d_{\rm H}(\underline{x}_1, \hspace{0.05cm}\underline{x}_2) = 5\hspace{0.05cm}, \hspace{0.4cm} d_{\rm H}(\underline{x}_1, \hspace{0.05cm}\underline{x}_3) = 3\hspace{0.05cm}, \hspace{0.4cm} d_{\rm H}(\underline{x}_2, \hspace{0.05cm}\underline{x}_3) = 2\hspace{0.05cm}.\]
- Eine wichtige Eigenschaft eines Codes $C$, die seine Korrekturfähigkeit wesentlich beeinflusst, ist die minimale Distanz zwischen zwei beliebigen Codeworten:
- \[d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}')\hspace{0.05cm}.\]
$\text{Definition:}$ Ein $(n, \hspace{0.05cm}k, \hspace{0.05cm}d_{\rm min})\text{ – Blockcode}$ besitzt die Codewortlänge $n$, die Informationsblocklänge $k$ und die minimale Distanz $d_{\rm min}$.
- Nach dieser Nomenklatur handelt es sich im hier betrachteten Beispiel um einen $(5, \hspace{0.05cm}2,\hspace{0.05cm} 2)$ – Blockcode.
- Manchmal verzichtet man auf die Angabe von $d_{\rm min}$ und spricht dann von einem $(n,\hspace{0.05cm} k)$ – Blockcode.
Beispiele für Fehlererkennung und Fehlerkorrektur
Die eben definierten Größen sollen nun an zwei Beispielen verdeutlicht werden.
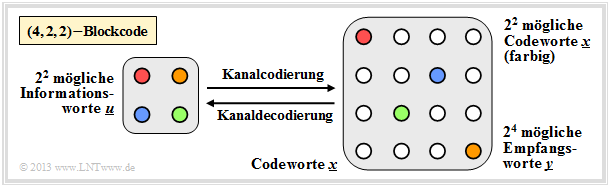
$\text{Beispiel 11:}$ $\text{(4, 2, 2)–Blockcode}$
In der Grafik verdeutlichen die nach rechts bzw. links zeigenden Pfeile den Codiervorgang bzw. die Decodierung:
- $$\underline{u_0} = (0, 0) \leftrightarrow (0, 0, 0, 0) = \underline{x_0}\hspace{0.05cm},\hspace{0.5cm} \underline{u_1} = (0, 1) \leftrightarrow (0, 1, 0, 1) = \underline{x_1}\hspace{0.05cm},$$
- $$\underline{u_2} = (1, 0) \leftrightarrow (1, 0, 1, 0) = \underline{x_2}\hspace{0.05cm},\hspace{0.5cm} \underline{u_3} = (1, 1) \leftrightarrow (1, 1, 1, 1) = \underline{x_3}\hspace{0.05cm}.$$
Rechts sind alle $2^4 = 16$ möglichen Empfangsworte $\underline{y}$ dargestellt:
- Von diesen können $2^n - 2^k = 12$ nur durch Bitfehler entstanden sein.
- Empfängt der Decoder ein solches „weißes” Codewort, so erkennt er zwar einen Fehler, er kann diesen aber wegen $d_{\rm min} = 2$ nicht korrigieren.
- Empfängt er beispielsweise $\underline{y} = (0, 0, 0, 1)$, so kann nämlich mit gleicher Wahrscheinlichkeit $\underline{x_0} = (0, 0, 0, 0)$ oder $\underline{x_1} = (0, 1, 0, 1)$ gesendet worden sein.
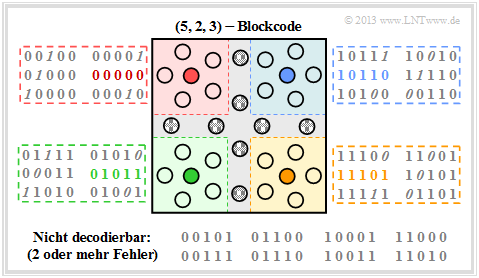
$\text{Beispiel 11:}$ $\text{(5, 2, 3)–Blockcode}$
Hier gibt es wegen $k=2$ vier gültige Codeworte :
- $$\underline{x_0} = (0, 0, 0, 0, 0)\hspace{0.05cm},\hspace{0.5cm} \underline{x_1} =(0, 1, 0, 1, 1)\hspace{0.05cm},$$
- $$\underline{x_2} =(1, 0, 1, 1, 0)\hspace{0.05cm},\hspace{0.5cm}\underline{x_3} =(1, 1, 1, 0, 1).$$
In der Grafik dargestellt ist die Empfängerseite, wobei man verfälschte Bit an der Kursivschrift erkennt.
- Von den $2^n - 2^k = 28$ unzulässigen Codeworten lassen sich nun $20$ einem gültigen Codewort (Füllfarbe: rot, grün, blau oder ocker) zuordnen, wenn man davon ausgeht, dass ein einziger Bitfehler wahrscheinlicher ist als deren zwei oder mehr.
- Zu jedem gültigen Codewort gibt es fünf unzulässige Codeworte mit jeweils nur einer Verfälschung ⇒ Hamming–Distanz $d_{\rm H} =1$. Diese sind in dem jeweiligen Quadrat mit roter, grüner, blauer oder ockerfarbenen Hintergrundfarbe angegeben.
- Die Fehlerkorrektur ist für diese aufgrund der minimalen Distanz $d_{\rm min} = 3$ zwischen den Codeworten möglich.
- Acht Empfangsworte sind nicht decodierbar. Beispielsweise könnte das Empfangswort $\underline{y} = (0, 0, 1, 0, 1)$ aus dem Codewort $\underline{x}_0 = (0, 0, 0, 0, 0)$ entstanden sein, aber auch aus dem Codewort $\underline{x}_3 = (1, 1, 1, 0, 1)$. In beiden Fällen wären zwei Bitfehler aufgetreten.
Zur Nomenklatur in diesem Buch
Eine Zielvorgabe unseres Lerntutorials $\rm LNTwww$ war, das gesamte Fachgebiet der Nachrichtentechnik und der zugehörigen Grundlagenfächer mit einheitlicher Nomenklatur zu beschreiben. In diesem zuletzt in Angriff genommenen Buch „ Kanalcodierung” müssen nun doch einige Änderungen hinsichtlich der Nomenklatur vorgenommen werden. Die Gründe hierfür sind:
- Die Codierungstheorie ist ein weitgehend in sich abgeschlossenes Fachgebiet und nur wenige Autoren von einschlägigen Fachbüchern zu diesem Gebiet versuchen, einen Zusammenhang mit anderen Aspekten der Digitalsignalübertragung herzustellen.
- Die Autoren der wichtigsten Bücher zur Kanalcodierung – englischsprachige und deutsche – verwenden weitgehend eine einheitliche Nomenklatur. Wir erlauben uns deshalb nicht, die Bezeichnungen zur Kanalcodierung in unser Übertragungstechnik–Schema zu pressen.
Einige Nomenklaturänderungen gegenüber den anderen $\rm LNTwww$–Büchern sollen hier genannt werden:
- Alle Signale werden durch Symbolfolgen in Vektorschreibweise dargestellt. Beispielsweise kennzeichnet $\underline{u} = (u_1, u_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, u_k)$ die Quellensymbolfolge und $\underline{v} = (v_1, v_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, v_k)$ die Sinkensymbolfolge. Bisher wurden diese Symbolfolgen mit $\langle q_\nu \rangle$ bzw. $\langle v_\nu \rangle$ bezeichnet.
- Der Vektor $\underline{x} = (x_1, x_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n)$ bezeichnet nun das zeitdiskrete Äquivalent zum Sendesignal $s(t)$, während das Empfangssignal $r(t)$ durch den Vektor $\underline{y} = (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$ beschrieben wird. Die Coderate ist der Quotient $R=k/n$ mit $0 \le R \le 1$ und die Anzahl der Prüfbits ergibt sich zu $m = n-k$.
- Im ersten Hauptkapitel sind die Elemente $u_i$ und $v_i$ $($jeweils mit Index $i = 1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, k)$ der Vektoren $\underline{u}$ und $\underline{v}$ stets binär $(0$ oder $1)$, ebenso wie die $n$ Elemente $x_i$ des Codewortes $\underline{x}$. Bei digitalem Kanalmodell (BSC, BEC, BSEC) gilt auch für die $n$ Empfangswerte $y_i \in \{0, 1\}$.
- Das AWGN–Kanalmodell ist durch reellwertige Ausgangswerte $y_i$ gekennzeichnet. Der Codewortschätzer gewinnt in diesem Fall aus dem Vektor $\underline{y} = (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$ den binären Vektor $\underline{z} = (z_1, z_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, z_n)$, der mit dem Codewort $\underline{x}$ zu vergleichen ist.
- Der Übergang von $\underline{y}$ auf $\underline{z}$ erfolgt durch Schwellenwertentscheidung ⇒ Hard Decision oder nach dem MAP–Kriterium ⇒ Soft Decision. Bei gleichwahrscheinlichen Eingangssymbolen führt die „Maximum Likelihood”–Schätzung ebenfalls zur minimalen Fehlerrate.
- Im Zusammenhang mit dem AWGN–Modell macht es Sinn, binäre Codesymbole $x_i$ bipolar (also $\pm1$) darzustellen. An den statistischen Eigenschaften ändert sich dadurch nichts. Wir kennzeichnen im Folgenden die bipolare Signalisierung durch eine Tilde. Dann gilt:
- \[\tilde{x}_i = 1 - 2 x_i = \left\{ \begin{array}{c} +1\\ -1 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls} \hspace{0.15cm} x_i = 0\hspace{0.05cm},\\ {\rm falls} \hspace{0.15cm}x_i = 1\hspace{0.05cm}.\\ \end{array}\]
Aufgaben zum Kapitel
Aufgabe 1.1: Zur Kennzeichnung aller Bücher
Aufgabe 1.2: Einfacher binärer Kanalcode
Aufgabe 1.2Z: 3D–Darstellung von Codes
Quellenverzeichnis
- ↑ Söder, G.: Modellierung, Simulation und Optimierung von Nachrichtensystemen. Berlin – Heidelberg: Springer, 1993.
- ↑ Kötter, R.; Mayer, T.; Tüchler, M.; Schreckenbach, F.; Brauchle, J.: Channel Coding. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, TU München, 2008.
- ↑ Liva, G.: Channel Coding. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, TU München und DLR Oberpfaffenhofen, 2010.