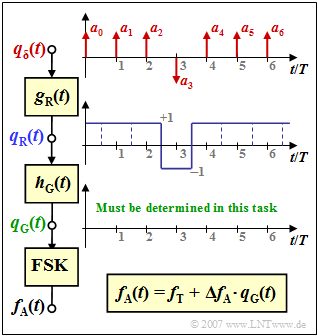
Exercise 3.5: GMSK Modulation

• Return to book

different signals of GMSK-Modulation

The modulation method used for GSM is  "Gaussian Minimum Shift Keying",  short  $\rm GMSK$.  This is a special type of  $\rm FSK$  ("Frequency Shift Keying")  with  $\rm CP-FSK$  ("Continuous Phase Matching"), where:

• The modulation index has the smallest value that just satisfies the orthogonality condition:   $h = 0.5$   ⇒   "Minimum Shift Keying"  $\rm (MSK)$,
• A Gaussian low-pass with the impulse response  $h_{\rm G}(t)$  is inserted before the FSK modulator, with the aim of saving even more bandwidth.

The graphic illustrates the situation:

• The digital message is represented by the amplitude coefficients  $a_{\mu} ∈ \{±1\}$  which are applied to a Dirac pulse.  It should be noted that the sequence drawn in is assumed for the subtask  (3).

• The symmetrical rectangular pulse with duration  $T = T_{\rm B}$  (GSM bit duration)  is dimensionless:

$$g_{\rm R}(t) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |\hspace{0.05cm} t \hspace{0.05cm}| < T/2 \hspace{0.05cm}, \\ |\hspace{0.05cm} t \hspace{0.05cm}| > T/2 \hspace{0.05cm}. \\ \end{array}$$

• This results for the rectangular signal

$$q_{\rm R} (t) = q_{\rm \delta} (t) \star g_{\rm R}(t) = \sum_{\nu} a_{\nu}\cdot g_{\rm R}(t - \nu \cdot T)\hspace{0.05cm}.$$

• The Gaussian low-pass is given by its frequency response or impulse response:

$$H_{\rm G}(f) = {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}[{f}/ ({2 f_{\rm G})} ]^2} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm G}(t) = 2 \cdot f_{\rm G} \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(2 f_{\rm G}\hspace{0.05cm}\cdot \hspace{0.05cm}t)^2}\hspace{0.05cm},$$

where the system theoretical cut-off frequency  $f_{\rm G}$  is used.  In the GSM specification, however, the 3dB cut-off frequency is specified with  $f_{\rm 3dB} = 0.3/T$ .  From this,  $f_{\rm G}$  can be calculated directly - see subtask  (2).

• The signal after the Gaussian low-pass is thus

$$q_{\rm G} (t) = q_{\rm R} (t) \star h_{\rm G}(t) = \sum_{\nu} a_{\nu}\cdot g(t - \nu \cdot T)\hspace{0.05cm}.$$

• Here  $g(t)$  is referred to as "frequency pulse":

$$g(t) = q_{\rm R} (t) \star h_{\rm G}(t) \hspace{0.05cm}.$$

• With the low-pass filtered signal  $q_{\rm G}(t)$, the carrier frequency  $f_{\rm T}$  and the frequency deviation  $\Delta f_{\rm A}$  for the instantaneous frequency at the output of the FSK modulator can thus be written:

$$f_{\rm A}(t) = f_{\rm T} + \Delta f_{\rm A} \cdot q_{\rm G} (t)\hspace{0.05cm}.$$

Notes:

• This exercise belongs to the chapter  Characteristics_of_GSM.
• Reference is also made to the chapter  Funkschnittstelle  in the book „Beispiele von Nachrichtensystemen”.

• For your calculations use the exemplary values  $f_{\rm T} = 900 \ \ \rm MHz$  and  $\Delta f_{\rm A} = 68 \ \rm kHz$.
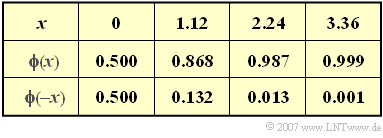
• Use the Gaussian integral to solve the task (some numerical values are given in the table)

Some Gaussian integral values

$$\phi(x) =\frac {1}{\sqrt{2 \pi}} \cdot \int^{x} _{-\infty} {\rm e}^{-u^2/2}\,{\rm d}u \hspace{0.05cm}.$$

Questionnaire

1

In what range of values can the instantaneous frequency  $f_{\rm A}(t)$  fluctuate? Which requirements must be met?

${\rm Max} \ \big[f_{\rm A}(t)\big] \ = \hspace{0.2cm}$ $\ \rm MHz$

${\rm Min} \ \big[f_{\rm A}(t)\big] \ = \hspace{0.28cm}$ $\ \rm MHz$

2

Which (normalized) system-theoretical cut-off frequency of the Gaussian low-pass results from the requirement  $f_{\rm 3dB} \cdot T = 0.3$?

$f_{\rm G} \cdot T \ = \ $

3

Calculate the frequency pulse  $g(t)$  using the function  $\phi (x)$. How large is the pulse value  $g(t = 0)$?

$g(t = 0) \ = \ $

4

Which signal value results for  $q_{\rm G}(t = 3T)$  with  $a_{3} = -1$  and  $a_{\mu \ne 3} = +1$? What is the instantaneous frequency  $f_{\rm A}(t = 3T)$?

$q_{\rm G}(t = 3T) \ = \ $

5

Calculate the pulse values  $g(t = ±T)$  of the frequency pulse

$g(t = ±T) \ = \ $

6

The amplitude coefficients are alternating. What is the maximum amount of  $q_{G}(t)$ ? Consider  $g(t ≥ 2 T) \approx 0$.

${\rm Max} \ |q_{\rm G}(t)| \ = \ $

Solution

Solution

(1)  If all amplitude coefficients $a_{\mu}$ are equal to $+1$, then $q_{\rm R}(t) = 1$ is a constant. Thus, the Gaussian low-pass has no influence and $q_{\rm G}(t) = 1$ results.

• The maximum frequency is thus

$${\rm Max}\ [f_{\rm A}(t)] = f_{\rm T} + \Delta f_{\rm A} \hspace{0.15cm} \underline {= 900.068\,{\rm MHz}} \hspace{0.05cm}.$$

• The minimum instantaneous frequency

$${\rm Min}\ [f_{\rm A}(t)] = f_{\rm T} - \Delta f_{\rm A} \hspace{0.15cm} \underline { = 899.932\,{\rm MHz}} \hspace{0.05cm}$$

is obtained when all amplitude coefficients are negative. In this case $q_{\rm R}(t) = q_{\rm G}(t) = -1$.

(2)  The frequency at which the logarithmic power transfer function is $3 \ \rm dB$ less than $f = 0$ is called the 3dB cut-off frequency.

• This can also be expressed as follows:

$$\frac {|H(f = f_{\rm 3dB})|}{|H(f = 0)|}= \frac{1}{\sqrt{2}} \hspace{0.05cm}.$$

• In particular the Gauss low-pass because of $H(f = 0) = 1$:

$$H(f = f_{\rm 3dB})= {\rm e}^{-\pi\cdot ({f_{\rm 3dB}}/{2 f_{\rm G}})^2} = \frac{1}{\sqrt{2}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}(\frac{f_{\rm 3dB}}{2 f_{\rm G}})^2 = \frac{{\rm ln}\hspace{0.1cm}\sqrt{2}}{\pi} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm G} = \sqrt{\frac{\pi}{4 \cdot {\rm ln}\hspace{0.1cm}\sqrt{2}}}\cdot f_{\rm 3dB}\hspace{0.05cm}.$$

• The numerical evaluation leads to $f_{\rm G} \approx 1.5 \cdot f_{\rm 3dB}$.
• From $f_{\rm 3dB} \cdot T = 0.3$ follows $f_{\rm G} \cdot T \underline{\approx 0.45}$.

(3)  The frequency pulse ${\rm g}(t)$ results from the convolution of the rectangular function $g_{\rm R}(t)$ with the pulse response $h_{\rm G}(t)$:

$$g(t) = g_{\rm R} (t) \star h_{\rm G}(t) = 2 f_{\rm G} \cdot \int^{t + T/2} _{t - T/2} {\rm e}^{-\pi\cdot (2 f_{\rm G}\cdot \tau)^2}\,{\rm d}\tau \hspace{0.05cm}.$$

• With the substitution $u^{2} = 8π \cdot {f_{G}}^{2} \cdot \tau^{2}$ and the function $\phi (x)$ you can also write for this:

$$g(t) = \ \frac {1}{\sqrt{2 \pi}} \cdot \int^{2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t + T/2)} _{2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t - T/2)} {\rm e}^{-u^2/2}\,{\rm d}u = \ \phi(2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t + T/2))- \phi(2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t - T/2)) \hspace{0.05cm}.$$

• For the time $t = 0$ is valid considering $\phi (-x) = 1 - \phi (x)$ and $f_{\rm G} \cdot T =$0.45

$$g(t = 0) = \ \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)- \phi(-\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)= \ 2 \cdot \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)-1 \approx 2 \cdot \phi(1.12)-1 \hspace{0.15cm} \underline {= 0.737} \hspace{0.05cm}.$$

(4)  With $a_{3} = +1$ the result would be $q_{\rm G}(t = 3 T) = 1$. Due to the linearity, the following therefore applies:

$$q_{\rm G}(t = 3 T ) = 1 - 2 \cdot g(t = 0)= 1 - 2 \cdot 0.737 \hspace{0.15cm} \underline {= -0.474} \hspace{0.05cm}.$$

(5)  With the result of (3) and $f_{\rm G} \cdot T =$0.45 you get

$$g(t = T) = \ \phi(3 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot T)- \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T) \approx \phi(3.36)-\phi(1.12) = 0.999 - 0.868 \hspace{0.15cm} \underline { = 0.131} \hspace{0.05cm}.$$

• The pulse value $g(t = -T)$ is exactly the same due to the symmetry of the Gaussian low-pass.

(6)  With alternating sequence, the absolute values $|q_{\rm G}(\mu \cdot T)|$ are all the same for all multiples of the bit duration $T$ for reasons of symmetry.

• All intermediate values at $t \approx \mu \cdot T$ are smaller.
• Taking $g(t ≥ 2T) \approx 0$ into account, each individual pulse value $g(0)$ is reduced by the preceding pulse with $g(t = T)$, and also by the following pulse with $g(t = -T)$.

• So there will be impulse interference and you get

$${\rm Max} \hspace{0.12cm}[q_{\rm G}(t)] = g(t = 0) - 2 \cdot g(t = T) = 0.737 - 2 \cdot 0.131 \hspace{0.15cm} \underline {= 0.475 }\hspace{0.05cm}.$$