Exercise 1.4Z: Representation of Oscillations

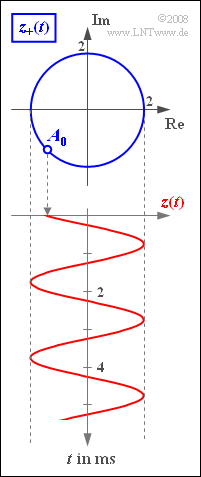
Two representations of a harmonic oscillation

Here, we consider a harmonic oscillation $z(t)$, which is shown in the graph together with the corresponding analytical signal $z_+(t)$. These signals can be described mathematically as follows:

$$z(t) = A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})= A_{\rm T} \cdot \cos(2 \pi f_{\rm T}( t - \tau)) \hspace{0.05cm},$$

$$ z_+(t) = A_{\rm 0} \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t+ϕ_{\rm T}}.$$

The two amplitude parameters $A_{\rm T} $ and $A_0$ are each dimensionless, the phase value $ϕ_{\rm T} $ is supposed to lie between $\text{±π}$, and the duration $τ$ is non-negative.

Subtask (4) refers to the equivalent low-pass signal $z_{\rm TP}(t)$, which is related to $z_+(t)$ as follows:

$$z_{\rm TP}(t) = z_+(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t}.$$

Further note that $ϕ_{\rm T}$ appears in the above equation with a positive sign. See "Notes on Nomenclature" below for reasons for the differential usage of $φ_{\rm T}$ and $ϕ_{\rm T} = – φ_{\rm T}$.

Notes on Nomenclature:

In this tutorial, as is common in other literature, the phase enters the equations with a negative sign when describing harmonic oscillations, Fourier series, and Fourier integrals. In the context of modulation methods, the phase is always given a plus sign.
To distinguish these two variants, we use $\phi_{\rm T}$ and $\varphi_{\rm T} = - \phi_{\rm T}$. Both symbols denote the lowercase Greek "phi", with the notation $\phi$ used predominantly in Anglo-American contexts, and $\varphi$ in German.
The phase values $\varphi_{\rm T} = 90^\circ$ and $\phi_{\rm T} = -90^\circ$ are thus equivalent and both represent the sine function:

$$\cos(2 \pi f_0 t - 90^{\circ}) = \cos(2 \pi f_0 t - \varphi_{\rm T}) = \cos(2 \pi f_0 t + \phi_{\rm T}) = \sin(2 \pi f_0 t ).$$

Further hints:

This exercise belongs to the chapter General Model of Modulation.
Particular reference is made to the page Describing the physical signal using the equivalent low-pass signal.
You will find further information on these topics in these chapters of the book „Signal Representation”:

(1) Harmonic Oscillation,

(2) Analytical Signal and its Spectral Function,

(3) Equivalent Low-Pass Signal and its Spectral Function.

In our tutorial $\rm LNTwww$, the plot of the analytical signal $s_+(t)$ n the complex plane is sometimes referred to as the "pointer diagram", while the "locus curve" gives the time course of the equivalent lowpass signal $s_{\rm TP}(t)$ . We refer you to the corresponding interactive Applets

(1) Physical and analytic signal,

(2) Physical signal and equivalent low-pass signal.

Questions

$A_{\rm T} \ = \ $

$f_{\rm T} \ = \ $

$\ \text{Hz}$

$\omega_{\rm T} \ = \ $

$\ \text{1/s}$

$\phi_{\rm T} \ = \ $

$\ \text{Grad}$

$τ \ = \ $

$\ \text{ms}$

$t_1 \ = \ $

$\ \text{ms}$

${\rm Re}\big[z_{\rm TP}(t = 1\ \rm ms)\big] \ = \ $

${\rm Im}\big[z_{\rm TP}(t = 1\ \rm ms)\big] \ = \ $

	The spectrum $Z(f)$ consists of two Dirac delta functions at $±f_{\rm T}$.
	The spectrum $Z_+(f)$ has one delta Dirac function at $–f_{\rm T}$.
	The spectrum $Z_{\rm TP}(f)$ contains a Dirac delta function at $f = 0$.
	The analytical signal $z_+(t)$ is always complex.
	The equivalent low-pass signal $z_{\rm TP}(t)$ is always complex.

Solution

(1) In the graphical representation of the time function $z(t)$ , one can identify

the (normalized) amplitude $A_{\rm T}\hspace{0.15cm}\underline{ = 2}$ and the period $T_0=2$ milliseconds.
Therefore, the signal frequency is $f_{\rm T} = 1/T_0\hspace{0.15cm}\underline{ = 500}$ Hz and the angular frequency is $ω_{\rm T}= 2πf_{\rm T} \hspace{0.15cm}\underline{ = 3141.5}$ 1/s.

(2) The analytical signal is generally:

$$z_+(t) = A_{\rm T} \cdot {\rm e}^{{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}(\omega_{\rm T}\cdot \hspace{0.05cm}t + \phi_{\rm T})} = A_{\rm T} \cdot {\rm e}^{{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \phi_{\rm T}} \cdot {\rm e}^{{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t }\hspace{0.05cm}.$$

At the same time the relationship:

$$A_0 = z_+(t = 0) = A_{\rm T} \cdot {\rm e}^{{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \phi_{\rm T}} \hspace{0.05cm}.$$

The complex amplitude $A_0$ can be read from the upper plot.

$$A_0 = - \sqrt{2} - {\rm j} \cdot \sqrt{2} = A_{\rm 0} \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} 0.75 \pi} \hspace{0.05cm}.$$

A comparison of both equations leads to the result:

$$ \phi_{\rm T} = - 0.75 \pi \hspace{0.15cm}\underline {= - 135^{\circ}} \hspace{0.05cm}.$$

Thereby, the following relationship exists with the duration $τ$:

$$\phi_{\rm T} = - 2 \pi \cdot f_{\rm T} \cdot \tau \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \tau = \frac{-\phi_{\rm T}}{2 \pi \cdot f_{\rm T}} = \frac{0.75 \pi}{2 \pi \cdot 0.5\,{\rm kHz}} \hspace{0.15cm}\underline {= 0.75 \,{\rm ms}} \hspace{0.05cm}.$$

(3) The analytical signal covers exactly one revolution in the time $T_0$ .

Thus, starting from $A_0$ after $t_1 = T_0/8\hspace{0.15cm}\underline{ = 0.25}$ ms, we reach the first moment that the analytical signal is imaginary:

$$z_+(t_1) = - 2 {\rm j}.$$

Because of the relation $z(t) = {\rm Re}[z_+(t)]$ , the first zero crossing of the signal $z(t)$ also occurs at time $t_1$ .

(4) Using the result from subtask (2), we obtain:

$$ z_{\rm TP}(t) = z_+(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm T}\cdot \hspace{0.05cm}t} = A_0 = A_{\rm T} \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \phi_{\rm T}} = {\rm const.}$$

Thus, for all times $t$ and hence also $t = 1$ ms:

$${\rm Re}[z_{\rm TP}(t)] = - \sqrt{2} \hspace{0.15cm}\underline {= -1.414} \hspace{0.05cm},$$

$$ {\rm Im}[z_{\rm TP}(t)] = - \sqrt{2}\hspace{0.15cm}\underline {= -1.414} \hspace{0.05cm}.$$

(5) Statements 1, 3 and 4 are correct:

The only Dirac function of $Z_+(f)$ is at $f = f_{\rm T}$ and not at $–f_{\rm T}$.
The analytical signal of a harmonic oscillation is always complex.
The equivalent lowpass signal of a harmonic oscillation is usually complex. The exception:

$$z(t) = ±A_{\rm T} · \cos(ω_{\rm T} · t) \ \Rightarrow \ z_{\rm TP}(t) = ±A_{\rm T}.$$