Contents
Residual sideband amplitude modulation
When transmitting signals using single sideband modulation $\rm (SSB–AM)$ the following problems occur:
- To suppress the unwanted sideband, a filter with a very high edge slope must be used.
- Such a steep-edged filters exhibit strong group delay distortions, especially at the limit of the passband.
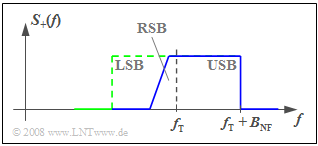
the problem can be greatly mitigated if instead single-sideband AM one uses residual sideband amplitude modulation $\rm (RSB–AM)$ , as shown in the adjacent graph.
The present description is based on the textbook [Mäu88][1]. According to it, the RSB-AM can be characterized as follows::
- A certain frequency range of the actually suppressed sideband – in the considered example of the LSB – is additionally used with a relatively flat decreasing transfer function.
- On the receiver side, a selection curve linearly increasing in frequency with a so-called "Nyquist edge" is used in the transition range from the suppressed sideband to the transmitted sideband.
- The demodulation performs a convolution of the sidebands around the carrier, so that as a result the message content of a band with the same amplitude for all frequencies is obtained.
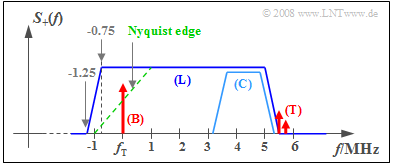
$\text{Example 1:}$ Anwendung findet das Restseitenbandverfahren beim (analogen) Farbfernsehen, dessen Frequenzspektrum nach der CCIR–Norm in der Grafik abgebildet ist. Die angegebenen Frequenzen beziehen sich auf das in Deutschland verwendete PAL–B/G–Fernsehformat.
Man erkennt aus dieser schematischen Darstellung:
- Das abgestrahlte Spektrum (es sind nur positive Frequenzen gezeichnet) reicht von $f_{\rm T} - 1.25 \ \rm MHz$ bis $f_{\rm T} + 5.75 \ \rm MHz$. Das untere Restseitenband ist also inklusive der Nyquistflanke ca. $1.25 \ \rm MHz$ breit.
- Die grün-gestrichelte Linie zeigt die Empfänger–Durchlasskurve. Der Bildträger (B) bei der Trägerfrequenz $f_{\rm T}$ liegt mittig zur Nyquistflanke.
- Das Luminanzsignal (L) geht bis etwa $5 \ \rm MHz$. Es enthält die Information für die Bildhelligkeit und die Farbe „Grün”.
- Im oberen Teil ist das Chromianzsignal (C) eingebettet. Dabei werden zwei orthogonale Träger bei $4.43 \ \rm MHz$ für „Rot” und „Blau” QAM–moduliert; der Träger wird dabei unterdrückt.
- Der Tonträger (T) liegt bei $f_{\rm T} + 5.5 \ \rm MHz$ und ist um $12 \ \rm dB$ niedriger als der Bildträger. Falls eine Stereo– oder Zweikanaltonübertragung vorliegt, folgt bei $5.75 \ \rm MHz$ ein zweiter Tonträger.
Quadrature Amplitude Modulation (QAM)
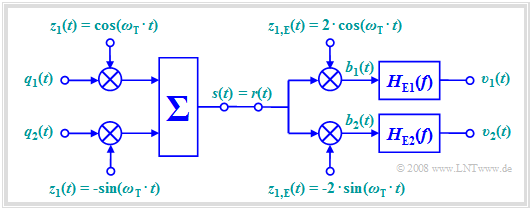
Durch Ausnutzung der Orthogonalität von Cosinus– und Sinusfunktion kann ein Kanal zur gleichzeitigen Übertragung zweier Quellensignale $q_1(t)$ und $q_2(t)$ ohne gegenseitige Beeinträchtigungen doppelt genutzt werden. Man bezeichnet dieses Verfahren als Quadratur–Amplitudenmodulation $\rm (QAM)$.
Das QAM–System weist folgende Eigenschaften auf:
- Das Sendesignal setzt sich aus zwei zueinander orthogonalen Anteilen zusammen:
- $$s(t) = q_1(t) \cdot \cos (\omega_{\rm T}\cdot t) - q_2(t) \cdot \sin (\omega_{\rm T}\cdot t)\hspace{0.05cm}.$$
- Bei frequenz– und phasensynchroner Demodulation lautet das Signal im oberen Zweig vor dem Tiefpass $H_{\rm E1}(f)$:
- $$b_1(t) = q_1(t) \cdot 2 \cdot \cos^2 (\omega_{\rm T}\cdot t) - q_2(t) \cdot 2 \cdot \cos (\omega_{\rm T}\cdot t)\cdot \sin (\omega_{\rm T}\cdot t)= q_1(t)\cdot \big[ 1 + \cos (2 \omega_{\rm T}\cdot t) \big] - q_2(t)\cdot \sin (2 \omega_{\rm T}\cdot t) \hspace{0.05cm}.$$
- Durch Begrenzung auf Frequenzen $|f| < f_{\rm T}$ ergibt sich somit im oberen bzw. unteren Zweig:
- $$v_1(t) = q_1(t),\hspace{0.3cm} v_2(t) = q_2(t)\hspace{0.05cm}.$$
- Bei einem Phasenversatz $Δϕ_{\rm T}$ zwischen den sende– und empfängerseitigen Trägersignalen kommt es neben einer Dämpfung des gewünschten Teilnehmers zusätzlich zu Übersprechen des zweiten Teilnehmers und damit zu nichtlinearen Verzerrungen:
- $$v_1(t) = \alpha_{11} \cdot q_1(t)+ \alpha_{12} \cdot q_2(t) \hspace{0.05cm}, \hspace{0.3cm} v_2(t) = \alpha_{21} \cdot q_1(t)+ \alpha_{22} \cdot q_2(t)$$
- $$\Rightarrow\hspace{0.3cm}\alpha_{11} = \alpha_{22} = \cos(\Delta \phi_{\rm T}) \hspace{0.05cm}, \hspace{0.3cm} \alpha_{12} = -\alpha_{21} = \sin(\Delta \phi_{\rm T}) \hspace{0.05cm}.$$
Inkohärente (nichtkohärente) Demodulation
Demodulatoren können in folgender Weise klassifiziert werden:
$\text{Definition:}$ Man bezeichnet einen Demodulator als kohärent, wenn er zur Rekonstruktion des Nachrichtensignals neben der erforderlichen Frequenzsynchronität auch genaue Informationen über die Phase des sendeseitigen Trägersignals $z(t)$ benötigt.
Ist diese Phaseninformation nicht erforderlich, so spricht man von einem inkohärenten Demodulator.
Ein Beispiel für einen inkohärenten (oder nichtkohärenten) Demodulator ist der Hüllkurvendemodulator.
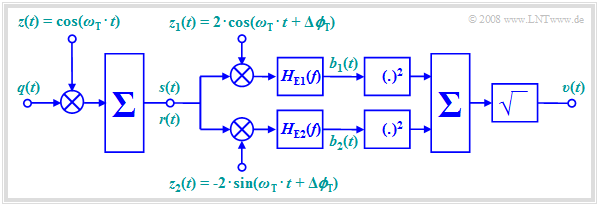
$\text{Beispiel 2:}$ Ein zweites Beispiel zeigt das folgende Blockschaltbild. Im Gegensatz zur Quadratur–Amplitudenmodulation wird hier die Orthogonalität zwischen Cosinus– und Sinusfunktion nicht zur gleichzeitigen Übertragung eines zweiten Quellensignals herangezogen, sondern zur Vereinfachung der Empfangseinrichtung genutzt.
Zu dieser Anordnung ist weiter anzumerken:
- Die empfängerseitigen Trägersignale können gegenüber den Trägersignalen beim Sender einen beliebigen und auch zeitabhängigen Phasenversatz $Δϕ_{\rm T}$ aufweisen, so lange die Phasendifferenz zwischen den beiden Zweigen weiterhin genau $90^\circ$ beträgt.
- Für die Signale im oberen und unteren Zweig – jeweils nach dem Multiplizierer und der Tiefpassfilterung – gilt nämlich:
- $$b_1(t) = \cos(\Delta \phi_{\rm T}) \cdot q(t), $$
- $$b_2(t) = -\sin(\Delta \phi_{\rm T}) \cdot q(t).$$
- Damit ist gewährleistet, dass das Sinkensignal $v(t)$ unabhängig vom Phasenversatz $Δϕ_{\rm T}$ mit dem Quellensignal $q(t)$ zumindest betragsmäßig übereinstimmt:
- $$v(t) = \sqrt{ b_1^2(t) + b_2^2(t)} = \sqrt{ q^2(t) } = \vert q(t) \vert \hspace{0.05cm}.$$
- Voraussetzung für die Funktionsfähigkeit – also für das Ergebnis $v(t) = q(t)$ – ist, dass zu allen Zeiten $q(t) ≥ 0$ ist. Bei einem analogen Nachrichtensystem könnte man diesen Sachverhalt beispielsweise mit dem Modulationsverfahren „ZSB–AM mit Träger” erzwingen.
- Angewandt wird diese Form von nichtkohärenter Demodulation – oder Modifikationen hiervon – vorwiegend bei einigen Digitalen Modulationsverfahren, die im vierten Kapitel dieses Buches ausführlich behandelt werden.
Aufgaben zum Kapitel
Aufgabe 2.12: Zur nichtkohärenten Demodulation
Aufgabe 2.13: Quadratur-Amplitudenmodulation (QAM)
Quellenverzeichnis
- ↑ Mäusl, R.: Analoge Modulationsverfahren. Heidelberg: Dr. Hüthig, 1988.