Contents
First Nyquist criterion in the time domain
For the entire first main chapter it was assumed that the detection of a symbol should not be affected by neighboring pulses. This is achieved by the detection of the signal
- $$d(t) = \sum \limits_{\it (\nu)} a_\nu \cdot g_d ( t - \nu T)$$
at the detection times $(\nu \cdot T)$ whenever the basic detection pulse $g_d(t)$
- is restricted to the range $|t| < T$, which was assumed for the last chapter Error Probability for Baseband Transmission, or
- has equidistant zero crossings at the detection times $\nu \cdot T$.
For the sake of simplicity, the noise component of the detection signal is assumed to be negligibly small in the following $(d_{\rm N}(t) =0)$.
$\text{Definition:}$ One denotes a basic detection pulse with the properties
- $$g_d ( t = \nu T)= 0 \hspace{0.3cm}{\rm{for} }\hspace{0.3cm} \nu = \pm 1, \pm 2,\pm 3,\hspace{0.05cm}\text{...}$$
as Nyquist pulse $g_{\hspace{0.05cm}\rm Nyq}(t)$, named after the physicist Harry Nyquist.
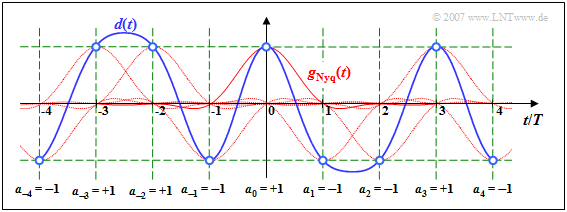
$\text{Example 1:}$ The diagram shows the detection signal $d(t)$ of such a Nyquist system. Dotted in red are the (weighted and shifted) Nyquist pulses $a_\nu \cdot g_{\hspace{0.05cm}\rm Nyq}(t -\nu \cdot T)$.
Please note:
- At the detection times, $d(\nu \cdot T) = a_\nu \cdot g_{\hspace{0.05cm}\rm Nyq}(0)$, as shown by the blue circles and green grid.
- The trailing pulses of the preceding pulses $(\nu < 0)$ as well as the leading pulses of the following pulses $(\nu > 0)$ do not affect the detection of the symbol $a_0$ in the Nyquist system.
For the sake of completeness, it should be mentioned that for this diagram the basic detection pulse
- $$g_{\hspace{0.05cm}\rm Nyq} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot t}{2 \cdot T}\right)$$
with trapezoidal spectrum and rolloff factor $r = 0.5$, which has already been discussed on the page Trapezoidal low-pass filter of the book "Linear Time Invariant Systems".
First Nyquist criterion in the frequency domain
Harry Nyquist formulated the condition for a intersymbol interfering free detection not only for the time domain, but in 1928 he also gave the corresponding criterion in the frequency domain.
$\text{First Nyquist criterion:}$ If the spectrum $G_d(f)$ of the basic detection pulse $g_d(t)$ fulfills the condition
- $$\sum \limits_{\it k = -\infty}^{+\infty} G_d \left ( f - \frac{k}{T} \right)= g_0 \cdot T = {\rm const.} \hspace{0.05cm}, $$
then $g_d(t)$ is a Nyquist pulse
- with equidistant zero crossings at the times $\nu \cdot T$ for $\nu \ne 0$ and
- the amplitude $g_d(t = 0) = g_0$.
Note: The proof follows on the next page.
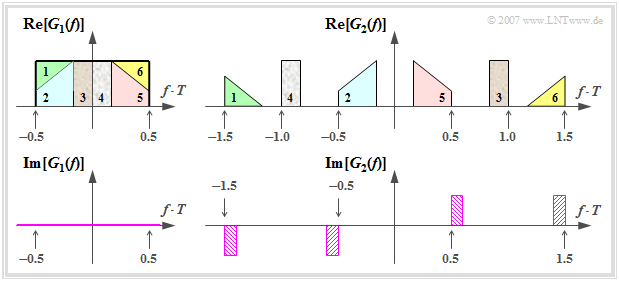
$\text{Example 2:}$ Sketched are two Nyquist spectra $G_1(f)$ and $G_2(f)$, which are composed of rectangular and triangular segments:
- The purely real spectrum sketched on the left
- $$G_1(f) \hspace{-0.05cm}=\hspace{-0.05cm} \left\{ \begin{array}{c} g_0 \cdot T \\ 0 \\ \end{array} \right. \begin{array}{*{1}c} \text{für} \\ \text{für} \\ \end{array}\begin{array}{*{20}c} \vert f \vert \hspace{-0.08cm}<\hspace{-0.08cm} {1}/(2T), \\ \vert f \vert \hspace{-0.08cm}>\hspace{-0.08cm} {1}/(2T) \\ \end{array}$$
- satisfies the condition formulated above with the smallest possible bandwidth. However, the associated Nyquist pulse $g_1(t) = g_0 \cdot {\rm si}(\pi \cdot t/T)$ decays very slowly, asymptotically with $1/t$.
- The real part of the spectrum $G_2(f)$ shown on the upper right was constructed from the rectangular spectrum $G_1(f)$ by shifting parts $1/T$ to the right or left.
$G_2(f)$ is also a Nyquist spectrum because of
- $$\sum \limits_{\it k = -\infty}^{+\infty} {\rm Re}\big[G_2 \left ( f - {k}/{T} \right)\big]= g_0 \cdot T \hspace{0.05cm}, \hspace{0.5cm}\sum \limits_{\it k = -\infty}^{+\infty} {\rm Im}\left[G_2 \big ( f - {k}/{T} \right)\big]= 0.$$
- In the imaginary part, the respective equally shaded parts, each $2/T$ apart, cancels out.
- However, the specification of the corresponding Nyquist pulse $g_2(t)$ is very complicated.
Proof of the first Nyquist criterion
(1) We start from the first Nyquist condition in the time domain:
- $$g_{\hspace{0.05cm}\rm Nyq}(\nu T) = \left\{ \begin{array}{c} g_0 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for} } \\ {\rm{for} } \\ \end{array}\begin{array}{*{20}c} \nu = 0 \hspace{0.05cm}, \\ \nu \ne 0 \hspace{0.1cm}. \\ \end{array}$$
(2) Thus, from the second Fourier integral, we obtain for $\nu \ne 0$:
- $$g_{\hspace{0.05cm}\rm Nyq}(\nu T) = \int_{-\infty}^{+\infty}G_{\rm Nyq}(f) \cdot {\rm e}^{ \hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi f \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.$$
(3) Decomposing the Fourier integral into partial integrals of width $1/T$, the conditional equations are:
- $$\sum_{k = -\infty}^{+\infty} \hspace{0.2cm} \int_{(k-1/2)/T}^{(k+1/2)/T}G_{\rm Nyq}(f) \cdot {\rm e}^{ \hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi f \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.$$
(4) With the substitution $f\hspace{0.08cm}' = f + k/T$ it follows:
- $$\sum_{k = -\infty}^{+\infty} \hspace{0.2cm} \int_{-1/(2T)}^{1/(2T)}G_{\rm Nyq}(f\hspace{0.08cm}' - \frac{k}{T} ) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm} (f\hspace{0.08cm}'- k/T) \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f \hspace{0.08cm}' = 0 \hspace{0.05cm}.$$
(5) For all integer values of $k$ and $\nu$ holds:
- $${\rm e}^{ - {\rm j} \hspace{0.05cm}2 \pi \hspace{0.05cm} k \hspace{0.05cm} \nu } = 1 \hspace{0.4cm} \Rightarrow \hspace{0.4cm}\sum_{k = - \infty}^{+\infty} \hspace{0.2cm} \int_{- 1/(2T)}^{1/(2T)}G_{\rm Nyq}(f\hspace{0.08cm}' - \frac{k}{T} ) \cdot {\rm e}^{ {\rm j} \hspace{0.05cm}2 \pi \hspace{0.02cm}f\hspace{0.08cm}' \hspace{0.02cm} \nu \hspace{0.05cm}T}\,{\rm d} f \hspace{0.08cm}' = 0 \hspace{0.05cm}.$$
(6) Swapping summation and integration and renaming $f\hspace{0.08cm}'$ to $f$, it further follows:
- $$\int_{-1/(2T)}^{1/(2T)}\hspace{0.2cm} \sum_{k = - \infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) \cdot {\rm e}^{ {\rm j} \hspace{0.05cm}2 \pi \hspace{0.02cm}f \hspace{0.02cm} \nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.$$
(7) This requirement can be satisfied for all $\nu \ne 0$ only if the infinite sum is independent of $f$, i.e., has a constant value:
- $$\sum_{k = -\infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) = K_{\rm Nyq} \hspace{0.05cm}.$$
(8) From the penultimate equation, we obtain simultaneously for $\nu = 0$:
- $$\int_{-1/(2T)}^{1/(2T)}\hspace{0.2cm} \sum_{k = -\infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) \,{\rm d} f = K_{\rm Nyq} \cdot \frac{1}{T} = g_0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}K_{\rm Nyq} = g_0 \cdot T \hspace{0.05cm}.$$
1/T Nyquist spectra
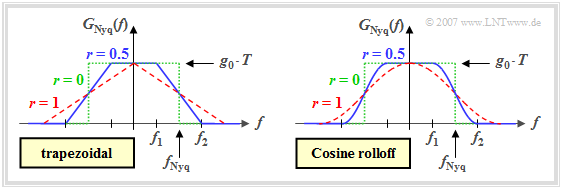
Nyquist spectra which are limited to the frequency range $-1/T \le f \le +1/T$ and are coherent are of particular importance for digital signal transmission. The diagram shows the trapezoidal characteristic and the cosine rolloff characteristic, which are two variants in this respect.
The same applies to both Nyquist spectra:
- The rolloff occurs between the two corner frequencies $f_1$ and $f_2$ point-symmetrically about the Nyquist frequency $f_{\rm Nyq} = (f_1+f_2)/2$. That is, for $0 \le f \le f_{\rm Nyq}$:
- $$G_{\rm Nyq}(f_{\rm Nyq}+f) + G_{\rm Nyq}(f_{\rm Nyq}-f) = g_0 \cdot T \hspace{0.05cm}.$$
- For all frequencies $|f| \le f_1$, $G_{\rm Nyq}(f)$ is constantly equal to $g_0 \cdot T$ and for $|f| \ge f_2$ it is identically zero. In the range between $f_1$ and $f_2$ holds:
- $$\frac{G_{\rm Nyq}(f)}{g_0 \cdot T } = \left\{ \begin{array}{c} \frac{f_2 - |f|}{f_2 -f_1 } \\ \\ \cos^2( \frac{\pi}{2}\cdot \frac{f_2 - |f|}{f_2 -f_1 }) \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{at \hspace{0.15cm}trapezoidal}\hspace{0.05cm},} \\ \\ {\rm{\rm{at \hspace{0.15cm}cosine \hspace{0.15cm}rolloff}}\hspace{0.05cm}.} \\ \end{array}$$
- To parameterize the slope, we use the rolloff factor $r$, which can take values between $0$ and $1$ (including these limits):
- $$r = \frac{f_2 -f_1 } {f_2 +f_1 } \hspace{0.05cm}.$$
- For $r = 0$ ⇒ $f_1 = f_2 = f_{\rm Nyq}$ we obtain the (green–dotted) rectangular Nyquist spectrum.
- The rolloff factor $r = 1$ ⇒ $f_1 = 0, \ f_2 = 2 f_{\rm Nyq}$ stands for a triangular and a $\cos^2$ spectrum, respectively – depending on which of the two basic structures shown above one assumes. These frequency curves are shown in red dashed lines.
Note: In the literature, the rolloff factor is sometimes also referred to as $\alpha$ ("alpha").
Time domain description of the 1/T Nyquist spectra
Let us now consider the Nyquist pulses. For the trapezoidal spectrum with rolloff factor $r$, we obtain:
- $$g_{_{\rm Trapezoid}} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot r \cdot t}{T}\right) \hspace{0.5cm}{\rm with }\hspace{0.5cm}{\rm si}(x) = {\rm sin}(x)/x .$$
In contrast, the Fourier inverse transform of the cosine rolloff spectrum (short: CRO spectrum) yields:
- $$g_{_{\rm CRO}} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot \frac{\cos(\pi \cdot r \cdot t/T)}{1 - (2 \cdot r \cdot t/T)^2 } \hspace{0.3cm}{\rm with }\hspace{0.3cm}{\rm si}(x) = {\rm sin}(x)/x.$$
These two Nyquist pulses can be viewed using the interactive applet Frequency & Impulse Responses $($with the setting $ \Delta \cdot f = 1)$, illustrating the influence of the rolloff factor $r$.
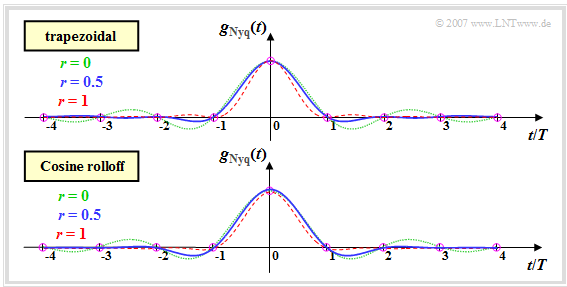
The following upper diagram shows the Nyquist pulse with trapezoidal spectrum for different rolloff factors. Below is the corresponding time course for the cosine rolloff spectrum. One can see:
- The smaller the rolloff factor $r$, the slower the decay of the Nyquist pulse. This statement is true for both the trapezoidal and cosine rolloff spectra.
- In the limiting case $r \to 0$, both cases yield the rectangular Nyquist spectrum and the $\rm si$–shaped Nyquist pulse, which decays asymptotically with $1/t$ (thin green curves).
- For an average rolloff $(r \approx 0.5)$, the first overshoots are smaller for the trapezoidal spectrum than for the CRO spectrum, because here the Nyquist slope is flatter for a given $r$ (blue curves).
- With the rolloff factor $r = 1$, the trapezoid becomes a triangle in the frequency domain and the CRO spectrum becomes the cosine–square spectrum. In the diagrams on the last page these spectral functions are drawn in red.
- Mit $r = 1$ erfolgt der asymptotische Abfall der oberen Zeitfunktion (gemäß dem Trapezspektrum) mit $1/t^2$ und der Abfall der unteren Zeitfunktion (gemäß dem CRO–Spektrum) mit $1/t^3$.
- Das bedeutet: Nach längerer Zeit ist der CRO–Nyquistimpuls besser eingeschwungen als der Trapez–Nyquistimpuls.
Zweites Nyquistkriterium
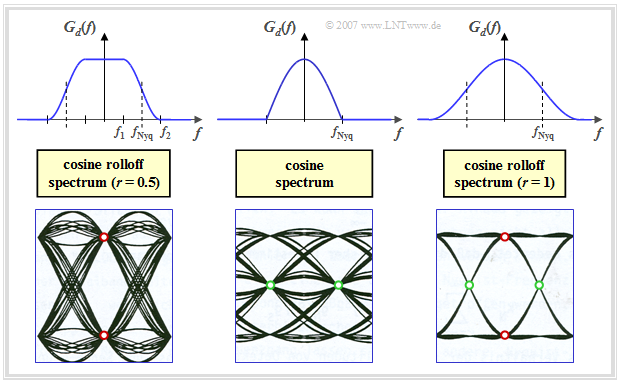
Vor der exakten mathematischen Definition soll anhand von Grafiken veranschaulicht werden, welche Bedeutung das zweite Nyquistkriterium zur Bewertung eines Digitalsystems besitzt. In der Grafik sind für drei Beispiele von Nyquistsystemen jeweils dargestellt:
- oben das Nyquistspektrum $G_d(f)$,
- unten das dazugehörige Augendiagramm im Vorgriff auf das dritte Hauptkapitel.
Interpretation:
- Die linke Grafik zeigt das Augendiagramm eines Nyquistsystems mit Cosinus–Rolloff–Charakteristik, wobei der Rolloff–Faktor $r= 0.5$ gewählt wurde. Da hier das erste Nyquistkriterium erfüllt ist (es besteht eine Punktsymmetrie um die Nyquistfrequenz $f_{\rm Nyq}$, ergibt sich für die vertikale Augenöffnung zum Zeitpunkt $t = 0$ der größtmögliche Wert $2 \cdot g_d(0)$. Alle Augenlinien gehen zum Zeitpunkt $t = 0$ durch einen der beiden rot markierten Punkte ⇒ das Auge ist vertikal maximal geöffnet.
- Das mittlere Spektrum weist keine Symmetrie bezüglich des Flankenabfalls auf, so dass hier das erste Nyquistkriterium nicht erfüllt ist – im Gegensatz zum zweiten. Alle Augenlinien schneiden hier die Zeitachse zu den selben Zeiten (markiert durch die grünen Punkte), was beispielsweise die Taktwiedergewinnung mittels einer PLL (Phase-Locked Loop ) erleichtert. Bei Erfüllung des zweiten Nyquistkriteriums ist die horizontale Augenöffnung maximal gleich der Symboldauer $T$ ⇒ das Auge ist horizontal maximal geöffnet.
- Das rechte Augendiagrammm verdeutlicht, dass beim CRO–Spektrum mit $r = 1$ sowohl das erste als auch das zweite Nyquistkriterium erfüllt werden. Der Nyquistimpuls
- $$g_d ( t )= g_0 \cdot \frac{\pi }{4}\cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot \left [ {\rm si}(\pi \cdot (\frac{t}{T} + \frac{1}{2}) + {\rm si}(\pi \cdot (\frac{t}{T} - \frac{1}{2})\right]$$
- weist hier die erforderlichen Nulldurchgänge bei $t = \pm T$, $t = \pm 1.5T$, $t = \pm 2T$, $t = \pm 2.5T$, ... auf, nicht jedoch bei $t = \pm 0.5T$. Die Impulsamplitude ist $g_d(t = 0) = g_0$. Hinweis: Kein anderer Impuls erfüllt gleichzeitig das erste und das zweite Nyquistkriterium.
$\text{Zusammenfassung der Nyquistkriterien:}$
(1) In Erinnerung an den Physiker Harry Nyquist bezeichnen wir einen Detektionsgrundimpuls $g_d( t)$ mit den Eigenschaften
- $$g_d ( t= 0) \ne 0, \hspace{1cm} g_d ( t)= 0 \hspace{0.3cm}{\rm{f\ddot{u}r} }\hspace{0.3cm} t = \pm T, \pm 2T,\pm 3T,\hspace{0.05cm}\text{...}$$
- als Nyquist–1–Impuls $g_{\hspace{0.05cm}\rm Nyq-1}(t)$. Dieser erfüllt das erste Nyquistkriterium und führt zur maximalen vertikalen Augenöffnung.
(2) Ein Impuls $g_{\hspace{0.05cm}\rm Nyq-2}(t)$, der das zweite Nyquistkriterium erfüllt, muss Nulldurchgänge bei $t = \pm 1.5T$, $t = \pm 2.5T$, ... besitzen:
- $$g_d ( t= 0.5) \ne 0, \hspace{0.8cm} g_d ( t)= 0 \hspace{0.3cm}{\rm{f\ddot{u}r} }\hspace{0.3cm} t = \pm 1.5T, \ \pm 2.5T,\ \pm 3.5T,\hspace{0.05cm}\text{...}$$
- Ein solcher Nyquist–2–Impuls führt zur maximalen horizontalen Augenöffnung.
(3) Ein Nyquist–2–Impuls kann immer als Summe zweier um $t = \pm T/2$ verschobener Nyquist–1–Impulse dargestellt werden:
- $$g_{\rm Nyq-2} ( t )= g_{\rm Nyq-1} ( t +T/2)+g_{\rm Nyq-1} ( t -T/2)\hspace{0.05cm}.$$
(4) Im Frequenzbereich lautet das zweite Nyquistkriterium (siehe [ST85] [1]):
- $$\sum_{k = -\infty}^{+\infty} \frac {G_d \left ( f -k/T \right)}{\cos(\pi \cdot f \cdot T - k \cdot \pi)}= {\rm const.}$$
$\text{Beispiel 3:}$ Ausgehend vom Nyquist–1–Impuls $g_{\rm Nyq-1}( t )= g_0 \cdot {\rm si}(\pi \cdot t/T)$ lautet der dazugehörige Nyquist–2–Impuls:
- $$g_{\rm Nyq-2}( t ) = g_0 \cdot \left [ {\rm si}(\pi \cdot \frac{t + T/2}{T}) + {\rm si}(\pi \cdot \frac{t- T/2}{T}) \right] =\frac{2 \cdot g_0}{\pi} \cdot \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\hspace{0.05cm}.$$
- Aufgrund der Begrenzung des Spektrums $G_{\rm Nyq-1}( f)$ auf den Bereich $\vert f \vert \le f_{\rm Nyq} = 1/(2T)$ beschränkt sich in obiger Gleichung (4) die Summe auf den Term mit $k = 0$ und man erhält:
- $$G_{\rm Nyq-2}(f) = \left\{ \begin{array}{c} g_0 \cdot T \cdot \cos(\pi/2 \cdot f/f_{\rm Nyq}) \\ \\ 0 \\\end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r} }\hspace{0.15cm} \vert f \vert < f_{\rm Nyq}\hspace{0.05cm}, \\ \\ {\rm{sonst} }\hspace{0.05cm}. \\ \end{array}$$
- Dieser Frequenzverlauf und das dazugehörige Augendiagramm ist in in der mittleren Spalte der obigen Grafik skizziert.
- Aus der unteren Grafik erkennt man deutlich die Erfüllung des zweiten Nyquistkriteriums.
Aufgaben zum Kapitel
Aufgabe 1.4Z: Komplexes Nyquistspektrum
Aufgabe 1.5: Cosinus-Quadrat-Spektrum
Quellenverzeichnis
- ↑ Söder, G.; Tröndle, K.: Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme. Berlin – Heidelberg: Springer, 1985.