Information Theoretical Limits of Channel Coding

1. Channel Coding
2. Binary Block Codes for Channel Coding
3. Information Theoretical Limits of Channel Coding

• Previous page
• Next page

• Previous page
• Next page

Channel coding theorem and channel capacity

We further consider a binary block code with  $k$  information bits per block and codewords of length  $n$, resulting in the code rate  $R=k/n$  with the unit "information bit/code symbol".

The ingenious information theorist  Claude E. Shannon  has dealt very intensively with the correctability of such codes already in 1948 and has given for this a limit for each channel which results from information-theoretical considerations alone. Up to this day, no code has been found which exceeds this limit, and this will remain so.

$\text{Shannon's channel coding theorem:}$  For each channel with channel capacity  $C > 0$  there always exists (at least) one code whose error probability approaches zero as long as the code rate  $R$  is smaller than the channel capacity  $C$. The prerequisite for this is that the following holds for the block length of this code:   $n \to \infty$.

Notes: 

• The statement "The error probability approaches zero" is not identical with the statement "The transmission is error-free". Example:   For an infinitely long sequence, finitely many symbols are corrupted.
• For some channels, even with  $R=C$  the error probability still goes towards zero (but not for all).

The inverse of the channel coding theorem is also true and states:

$\text{Inverse:}$  If the code rate  $R$  is larger than the channel capacity  $C$, then an arbitrarily small error probability cannot be achieved in any case

.

To derive and calculate the channel capacity, we first assume a digital channel with  $M_x$  possible input values  $x$  and  $M_y$  possible output values  $y$ . Then, for the mean mutual information– briefly, the  "mutual information"  – between the random variable  $x$  at the channel input and the random variable  $y$  at its output:

\[I(x; y) =\sum_{i= 1 }^{M_X} \hspace{0.15cm}\sum_{j= 1 }^{M_Y} \hspace{0.15cm}{\rm Pr}(x_i, y_j) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_i)}{{\rm Pr}(y_j)} = \sum_{i= 1 }^{M_X} \hspace{0.15cm}\sum_{j= 1 }^{M_Y}\hspace{0.15cm}{\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_i) \cdot {\rm Pr}(x_i) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_i)}{\sum_{k= 1}^{M_X} {\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_k) \cdot {\rm Pr}(x_k)} \hspace{0.05cm}.\]

In the transition from the first to the second equation, the  "Theorem of Bayes"  and the  "Theorem of Total Probability"  were considered.

Further, it should be noted:

• The binary logarithm   is denoted here with "log₂". Partially, we also use "ld" (Logarithmus dualis in German) for this in our learning tutorial .
• In contrast to the book  "Information Theory"  we do not distinguish in the following between the random variable $($upper case letters  $X$  or  $Y)$  and the realizations $($lower case letters  $x$  bzw.  $y)$.
  

$\text{Definition:}$  The  channel capacity'  introduced by Shannon gives the maximum mutual information  $I(x; y)$  between the input variable  $x$  and the output variable  $y$  :

\[C = \max_{{{\rm Pr}(x_i)}} \hspace{0.1cm} I(X; Y) \hspace{0.05cm}.\]

The pseudo–unit "bit/channel use" must be added.

Since the maximization of the mutual information must be done over all possible (discrete) input distributions  ${\rm Pr}(x_i)$  the channel capacity is independent of the input and thus a pure channel parameter.

Channel capacity of the BSC model

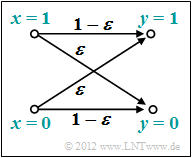
We now apply these definitions to the  "BSC model"  (Binary Symmetric Channel ):

\[I(x; y) = {\rm Pr}(y = 0 \hspace{0.03cm}| \hspace{0.03cm}x = 0) \cdot {\rm Pr}(x = 0) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(y = 0 \hspace{0.03cm}| \hspace{0.03cm}x = 0)}{{\rm Pr}(y = 0)} + {\rm Pr}(y = 1 \hspace{0.03cm}| \hspace{0.03cm}x = 0) \cdot {\rm Pr}(x = 0) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(Y = 1 \hspace{0.03cm}| \hspace{0.03cm}x = 0)}{{\rm Pr}(y = 1)} + \]

\[\hspace{1.45cm} + \hspace{0.15cm}{\rm Pr}(y = 0 \hspace{0.05cm}| \hspace{0.05cm}x = 1) \cdot {\rm Pr}(x = 1) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(Y = 0 \hspace{0.05cm}| \hspace{0.05cm}x = 1)}{{\rm Pr}(y = 0)} + {\rm Pr}(y = 1 \hspace{0.05cm}| \hspace{0.05cm}x = 1) \cdot {\rm Pr}(x = 1) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(y = 1 \hspace{0.05cm}| \hspace{0.05cm}x = 1)}{{\rm Pr}(y = 1)} \hspace{0.05cm}.\]

BSC channel model

The channel capacity is arrived at by the following considerations:

• Maximization with respect to the input distribution leads to equally probable symbols:

\[{\rm Pr}(x = 0) = {\rm Pr}(x = 1) = 1/2 \hspace{0.05cm}.\]

• Due to the symmetry evident from the model, the following then holds simultaneously:

\[{\rm Pr}(y = 0) = {\rm Pr}(y = 1) = 1/2 \hspace{0.05cm}.\]

• We also consider the BSC transmission probabilities:

\[{\rm Pr}(y = 1 \hspace{0.05cm}| \hspace{0.05cm}x = 0) = {\rm Pr}(y = 0 \hspace{0.05cm}| \hspace{0.05cm}x = 1) = \varepsilon \hspace{0.05cm},\]

\[{\rm Pr}(y = 0 \hspace{0.05cm}| \hspace{0.05cm}x = 0) = {\rm Pr}(y = 1 \hspace{0.05cm}| \hspace{0.05cm}x = 1) = 1-\varepsilon \hspace{0.05cm}.\]

• After combining two terms each, we thus obtain:

\[C \hspace{0.15cm} = \hspace{0.15cm} 2 \cdot 1/2 \cdot \varepsilon \cdot {\rm log_2 } \hspace{0.15cm}\frac{\varepsilon}{1/2 }+ 2 \cdot 1/2 \cdot (1- \varepsilon) \cdot {\rm log_2 } \hspace{0.15cm}\frac{1- \varepsilon}{1/2 } \varepsilon \cdot {\rm ld } \hspace{0.15cm}2 - \varepsilon \cdot {\rm log_2 } \hspace{0.15cm} \frac{1}{\varepsilon }+ (1- \varepsilon) \cdot {\rm log_2 } \hspace{0.15cm} 2 - (1- \varepsilon) \cdot {\rm log_2 } \hspace{0.15cm}\frac{1}{1- \varepsilon}\]

\[\Rightarrow \hspace{0.3cm} C \hspace{0.15cm} = \hspace{0.15cm} 1 - H_{\rm bin}(\varepsilon). \]

• The binary entropy function is used here:

\[H_{\rm bin}(\varepsilon) = \varepsilon \cdot {\rm log_2 } \hspace{0.15cm}\frac{1}{\varepsilon}+ (1- \varepsilon) \cdot {\rm log_2 } \hspace{0.15cm}\frac{1}{1- \varepsilon}\hspace{0.05cm}.\]

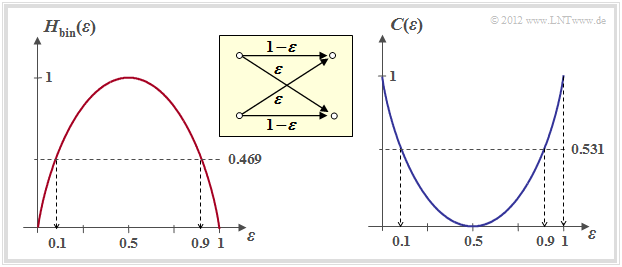
The following right graph shows the BSC channel capacity depending on the corruption probability  $\varepsilon$. On the left, for comparison, the binary entropy function is shown, which has already been defined in the chapter  "memoryless sources"  of the book "Information Theory".

Kanalkapazität des BSC–Modells

One can see from this representation:

• The corruption probability  $\varepsilon$  leads to the channel capacity $C(\varepsilon)$. According to the  "channel coding theorem"  error-free decoding is only possible if the code rate $R$ is not greater than  $C(\varepsilon)$.

• With  $\varepsilon = 10\%$  error-free decoding is impossible because of  $C(0.1) = 0.531$  if the code rate  $R > 0.531$ . At 50–percent corruption, error-free decoding is impossible even if the code rate is arbitrarily small:   $C(0.5) = 0$ .
  

• From an information theory point of view  $\varepsilon = 1$  (inversion of all bits) is equivalent to  $\varepsilon = 0$  (error-free transmission). Similarly  $\varepsilon = 0.9$  is equivalent to  $\varepsilon = 0.1$. Error-free decoding is achieved here by swapping the zeros and ones, i.e. by a so-called mapping.
  

Channel capacity of the AWGN model

AWGN channel model

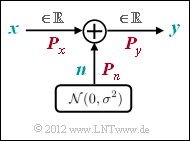
We now consider the  AWGN channel  (Additive White Gaussian Noise ). Here, for the output signal  $y = x + n$, where  $n$  describes a  Gaussian distributed random variable  and it applies to their expected values (moments):

$${\rm E}[n] = 0,\hspace{1cm} {\rm E}[n^2] = P_n.$$

Thus, regardless of the input signal  $x$  (analog or digital), there is always a continuous value output signal  $y$, and in the  equation for transinformation  is to be used  $M_y \to\infty$ .

The calculation of the channel capacity for the AWGN channel is given here only in keywords. The exact derivation can be found in the fourth main chapter "Discrete Value Information Theory" of the book  "Information theory".

• The input quantity  $x$  optimized with respect to maximum mutual information will certainly be value continuous, that is, for the AWGN channel, in addition to  $M_y \to\infty$  also  $M_x \to\infty$ holds.

• While for discrete value input optimization is to be done over all  ${\rm Pr}(x_i)$  now optimization is done using the  PDF  $f_x(x)$ of the input signal under the constraint  Power Limitation:

\[C = \max_{f_x(x)} \hspace{0.1cm} I(x; y)\hspace{0.05cm},\hspace{0.3cm}{\rm wobei \hspace{0.15cm} gelten \hspace{0.15cm} muss} \text{:}\hspace{0.15cm} {\rm E} \left [ x^2 \right ] \le P_x \hspace{0.05cm}.\]

• The optimization also yields a Gaussian distribution for the input PDF   ⇒   $x$,  $n$  and  $y$  are Gaussian distributed according to the density functions  $f_x(x)$,  $f_n(n)$  and  $f_y(y)$. We name the corresponding powers  $P_x$,  $P_n$  and  $P_y$.
  

• After longer calculation one gets for the channel capacity using the binary logarithm  $\log_2(\cdot)$ – again with the pseudo unit "bit/channel use":

\[C = {\rm log_2 } \hspace{0.15cm} \sqrt{\frac{P_y}{P_n }} = {\rm log_2 } \hspace{0.15cm} \sqrt{\frac{P_x + P_n}{P_n }} = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 + \frac{P_x}{P_n } \right )\hspace{0.05cm}.\]

• If  $x$ describes a  discrete-time signal with symbol rate  $1/T_{\rm S}$, it must be bandlimited to  $B = 1/(2T_{\rm S})$  bandlimited, and the same bandwidth  $B$  must be applied to the noise signal  $n$  ⇒   "noise bandwidth":

\[P_X = \frac{E_{\rm S}}{T_{\rm S} } \hspace{0.05cm}, \hspace{0.4cm} P_N = \frac{N_0}{2T_{\rm S} }\hspace{0.05cm}. \]

• Thus, the AWGN channel capacity can also be expressed by the  transmit energy per symbol $(E_{\rm S})$  and the  noise power density  $(N_0)$:

\[C = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 + {2 E_{\rm S}}/{N_0 } \right )\hspace{0.05cm}, \hspace{1.9cm} \text {Einheit:}\hspace{0.3cm} \frac{\rm bit}{\rm Kanalzugriff}\hspace{0.05cm}.\]

• The following equation gives the channel capacity per unit time (denoted by $^{\star})$:

\[C^{\star} = \frac{C}{T_{\rm S} } = B \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 + {2 E_{\rm S}}/{N_0 } \right )\hspace{0.05cm}, \hspace{0.8cm} \text {Einheit:} \hspace{0.3cm} \frac{\rm bit}{\rm Zeiteinheit}\hspace{0.05cm}.\]

$\text{Example 1:}$ 

• Für  $E_{\rm S}/N_0 = 7.5$   ⇒   $10 \cdot \lg \, E_{\rm S}/N_0 = 8.75 \, \rm dB$  erhält man die Kanalkapazität  $C = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm} (16) = 2 \, \rm bit/Kanalzugriff$.
• For a channel with the (physical) bandwidth  $B = 4 \, \rm kHz$, which corresponds to the sampling rate  $f_{\rm A} = 8\, \rm kHz$  also  $C^\star = 16 \, \rm kbit/s$.

However, a comparison of different coding methods at constant  $E_{\rm S}$  (energy per transmitted symbol ) is not fair. Rather, for this comparison, the energy  $E_{\rm B}$  per useful bit  should be fixed. The following relationships apply:

\[E_{\rm S} = R \cdot E_{\rm B} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} E_{\rm B} = E_{\rm S} / R \hspace{0.05cm}. \]

$\text{Channel Coding Theorem for the AWGN channel:}$ 

Error-free decoding $($at infinitely long blocks   ⇒   $n \to \infty)$  is always possible if the code rate  $R$  is smaller than the channel capacity  $C$:

\[R < C = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 +2 \cdot R\cdot E_{\rm B}/{N_0 } \right )\hspace{0.05cm}.\]

For each code rate&nbsp $R$  the required  $E_{\rm B}/N_0$  of the AWGN channel can thus be determined so that error-free decoding is just possible. One obtains for the limiting case  $R = C$:

\[{E_{\rm B} }/{N_0} > \frac{2^{2R}-1}{2R } \hspace{0.05cm}.\]

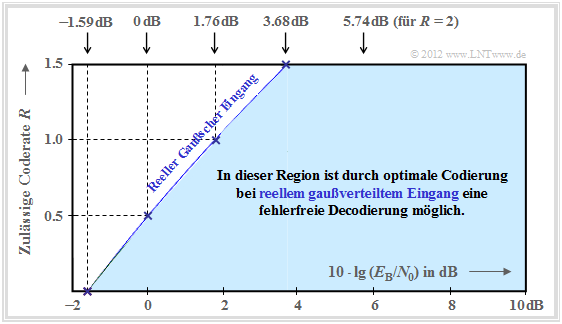
The graph summarizes the result, with the ordinate  $R$  plotted on a linear scale and the abscissa  $E_{\rm B}/{N_0 }$  plotted logarithmically.

Channel capacity of the AWGN channel

• Error-free coding is not possible outside the blue area.
• The blue limit curve indicates the channel capacity  $C$  of the AWGN channel.
  

From this graph and the above equation, the following can be deduced:

• Channel capacity  $C$  increases somewhat less than linearly with  $10 \cdot \lg \, E_{\rm B}/N_0 $ . In the graph, some selected function values are indicated as blue crosses.
  

• If  $10 \cdot \lg \, E_{\rm B}/N_0 < -1.59 \, \rm dB$, error-free decoding is impossible in principle. If the code rate  $R = 0.5$, then  $10 \cdot \lg \, E_{\rm B}/N_0 > 0 \, \rm dB$  must be   ⇒  $E_{\rm B} > N_0$.
  

• Für alle binären Codes gilt per se  $0 < R ≤ 1$. Only with non-binary codes code rates  $R > 1$  are possible. For example, the maximum possible code rate of a quaternary code  $R = \log_2 \, M_y = \log_2 \, 4 = 2$.
  

• All one-dimensional modulation types – i.e., those methods that use only the in-phase– or only the quadrature component such as  2–ASK, 

BPSK  and  2–FSK  – must be in the blue area of the present graphic.

• As shown in the chapter  Maximum code rate for QAM–structures  of the book "Information Theory" is shown, there is a "friendlier" limit curve for two-dimensional modulation types such as the  Quadrature–Amplitude Modulation .

AWGN–Kanalkapazität für binäre Eingangssignale

In diesem Buch beschränken wir uns vorwiegend auf binäre Codes, also auf das Galoisfeld  ${\rm GF}(2^n)$. Damit ist

Bedingte Dichtefunktionen bei AWGN–Kanal und binärem Eingang

• zum einen die Coderate auf den Bereich  $R ≤ 1$  begrenzt,
  
• zum zweiten auch für  $R ≤ 1$  nicht die gesamte blaue Region verfügbar (siehe vorherige Seite).

Die nun gültige Region ergibt sich aus der  allgemeinen Gleichung  der Transinformation durch

• die Parameter  $M_x = 2$  und  $M_y \to \infty$,
  
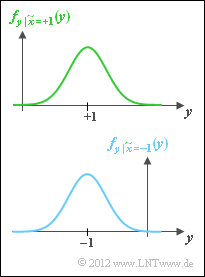
• bipolare Signalisierung   ⇒   $x=0$   →   $\tilde{x} = +1$  und  $x=1$   →   $\tilde{x} = -1$,
  
• den Übergang von bedingten Wahrscheinlichkeiten  ${\rm Pr}(\tilde{x}_i)$  zu bedingten Wahrscheinlichkeitsdichtefunktionen,
  
• Ersetzen der Summe durch eine Integration.
  
  

Die Optimierung der Quelle führt auf gleichwahrscheinliche Symbole:

\[{\rm Pr}(\tilde{x} = +1) = {\rm Pr}(\tilde{x} = -1) = 1/2 \hspace{0.05cm}. \]

Damit erhält man für das Maximum der Transinformation, also für die Kanalkapazität:

\[C \hspace{-0.15cm} = {1}/{2} \cdot \int_{-\infty }^{+ \infty} \left [ f_{y\hspace{0.05cm} |\hspace{0.05cm}\tilde{x} = +1}(y)\cdot {\rm log_2 } \hspace{0.15cm}\frac {f_{y\hspace{0.05cm} |\hspace{0.05cm}\tilde{x} = +1}(y)}{f_y(y)} + f_{y\hspace{0.05cm} |\hspace{0.05cm}\tilde{x} = -1}(y)\cdot {\rm log_2 } \hspace{0.15cm}\frac {f_{y\hspace{0.05cm} |\hspace{0.05cm}\tilde{x} = -1}(y)}{f_y(y)} \right ]\hspace{0.1cm}{\rm d}y \hspace{0.05cm}.\]

Das Integral lässt sich nicht in mathematisch–geschlossener Form lösen, sondern kann nur numerisch ausgewertet werden.

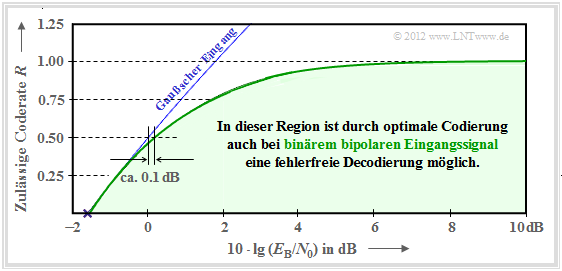
• Die grüne Kurve zeigt das Ergebnis.
• Die blaue Kurve gibt zum Vergleich die auf der letzten Seite hergeleitete Kanalkapazität für gaußverteilte Eingangssignale an.

AWGN–Kanalkapazität für binäre Eingangssignale

Man erkennt:

• Für  $10 \cdot \lg \, E_{\rm B}/N_0 < 0 \, \rm dB$  unterscheiden sich die beiden Kapazitätskurven nur geringfügig.
• So muss man bei binärem bipolaren Eingang gegenüber dem Optimum (Gaußscher Eingang) die Kenngröße  $10 \cdot \lg \, E_{\rm B}/N_0$  nur etwa um  $0.1 \, \rm dB$  erhöhen, um ebenfalls die Coderate  $R = 0.5$  zu ermöglichen.
  

• Ab  $10 \cdot \lg \, E_{\rm B}/N_0 \approx6 \, \rm dB$  ist die Kapazität  $C = 1 \, \rm bit/Kanalzugriff$  des AWGN–Kanals für binären Eingang (fast) erreicht.
• Dazwischen verläuft die Grenzkurve annähernd exponentiell ansteigend.

Gebräuchliche Kanalcodes im Vergleich zur Kanalkapazität

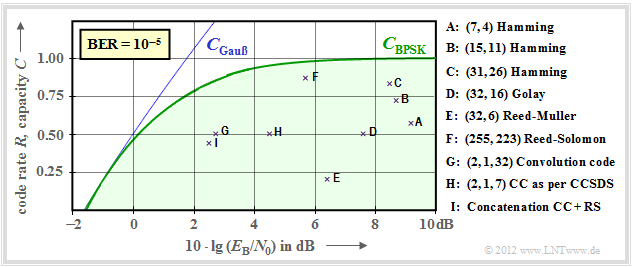
Nun soll gezeigt werden, in wie weit sich etablierte Kanalcodes der BPSK–Kanalkapazität (grüne Kurve) annähern. In der folgenden Grafik ist als Ordinate die Rate  $R=k/n$  dieser Codes bzw. die Kapazität  $C$  (mit der zusätzlichen Pseudo–Einheit "bit/Kanalzugriff") aufgetragen. Weiter ist vorausgesetzt:

• der AWGN–Kanal, gekennzeichnet durch  $10 \cdot \lg \, E_{\rm B}/N_0$  in dB, und
  

• für die durch Kreuze markierten Codes eine Bitfehlerrate (BER) von  $10^{-5}$.
  

Rates and required  $E_{\rm B}/{N_0}$  of different channel codes

$\text{Bitte beachten Sie:}$ 

• Die Kanalkapazitätskurven gelten stets für  $n \to \infty$  und  $\rm BER \to 0$  gelten.
• Würde man diese strenge Forderung "fehlerfrei" auch an die betrachteten Kanalcodes endlicher Codelänge  $n$  anlegen, so wäre hierfür stets  $10 \cdot \lg \, E_{\rm B}/N_0 \to \infty$  erforderlich.
• Dies ist aber ein akademisches Problem, das für die Praxis wenig Bedeutung hat. Für  $\rm BER = 10^{-10}$  ergäbe sich eine qualitativ und auch quantitativ ähnliche Grafik.
  

Es folgen einige Erläuterungen zu den Daten, die der Vorlesung [Liv10] entnommen wurden:

• Die Punkte  $\rm A$,  $\rm B$  und  $\rm C$  markieren  Hamming–Codes  unterschiedlicher Rate. Sie alle benötigen für  $\rm BER = 10^{-5}$  mehr alss  $10 \cdot \lg \, E_{\rm B}/N_0 = 8 \, \rm dB$.
• Die Markierung  $\rm D$  kennzeichnet den binären  Golay–Code  mit der Rate  $1/2$  und die Markierung  $\rm E$  einen  Reed–Muller–Code. Dieser sehr niederratige Code kam bereits 1971 bei der Raumsonde Mariner 9 zum Einsatz.
• Die  Reed–Solomon–Codes  (RS–Codes) werden im zweiten Hauptkapitel ausführlich behandelt. Mit  $\rm F$  markiert ist ein hochratiger RS–Code  $(R = 223/255 > 0.9)$  und einem erforderlichen  $10 \cdot \lg \, E_{\rm B}/N_0 < 6 \, \rm dB$.
• Die Markierungen  $\rm G$  und  $\rm H$  bezeichnen beispielhafte  Faltungscodes  (englisch:   Convolutional Codes, CC) mittlerer Rate. Der Code  $\rm G$  wurde schon 1972 bei der Pioneer10–Mission eingesetzt.
• Die Kanalcodierung der Voyager–Mission Ende der 1970er Jahre ist mit  $\rm I$  markiert. Es handelt sich um die Verkettung eines  $\text{(2, 1, 7)}$–Faltungscodes mit einem Reed–Solomon–Code, wie im vierten Hauptkapitel beschrieben.
  
  

Anmerkung:   Bei den Faltungscodes hat insbesondere der dritte Kennungsparameter eine andere Bedeutung als bei den Blockcodes. $\text{CC (2, 1, 32)}$  weist beispielsweise auf das Memory  $m = 32$  hin.

Raten und erforderliches  $E_{\rm B}/N_0$  für iterative Codierverfahren

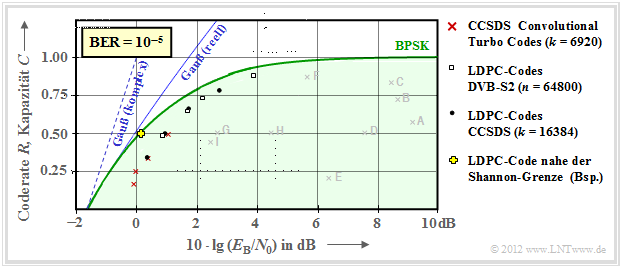
Mit iterativer Decodierung lassen sich deutlich bessere Ergebnisse erzielen, wie die zweite Grafik zeigt.

• Das heißt:  Die einzelnen Markierungspunkte liegen sehr viel näher an der Kapazitätskurve.
  
• Die bisher mit "Gauß–Kapazität" beschriftete durchgezogene blaue Kurve wird hier "Gauß (reell)" genannt.

Hier noch einige weitere Erläuterungen zu dieser Grafik:

• Rote Kreuze markieren sogenannte  Turbocodes  nach  CCSDS  (Consultative Committee for Space Data Systems ) mit jeweils  $k = 6920$  Informationsbits und unterschiedlichen Codelängen  $n$. Diese von  Claude Berrou  um 1990 erfundenen Codes können iterativ decodiert werden. Die (roten) Markierungen liegen jeweils weniger als  $1 \, \rm dB$  von der Shannon–Grenze entfernt.
  

• Ähnliches Verhalten zeigen die durch weiße Rechtecke gekennzeichneten  LDPC–Codes  (Low Density Parity–check Codes ), die seit 2006 bei  DVB–S(2)  (Digital Video Broadcast over Satellite ) eingesetzt werden. Diese eignen sich aufgrund der spärlichen Belegung der Prüfmatrix  $\boldsymbol {\rm H}$  (mit Einsen) sehr gut für die iterative Decodierung mittels Faktor–Graphen   und   Exit Charts. Siehe [Hag02]
  

• Die schwarzen Punkte markieren die von CCSDS spezifizierten  LDPC–Codes, die alle von einer konstanten Anzahl von Informationsbits ausgehen  $(k = 16384)$. Dagegen ist bei allen weißen Rechtecken die Codelänge  $n = 64800$  konstant, während sich die Anzahl  $k$  der Informationsbits entsprechend der Rate  $R = k/n$  ändert.
  

• Um das Jahr 2000 hatten viele Forscher den Ehrgeiz, sich der Shannon–Grenze bis auf Bruchteile von einem  $\rm dB$  anzunähern. Das gelbe Kreuz markiert ein solches Ergebnis aus [CFRU01]. Verwendet wurde ein irregulärer Rate–1/2–LDPC–Code der Codelänge  $n = 2 \cdot10^6$.
  
  

$\text{Fazit:}$  Festzuhalten ist, dass Shannon bereits 1948 erkannt und nachgewiesen hat, dass kein eindimensionales Modulationsverfahren links von der durchgehend eingezeichneten AWGN–Grenzkurve "Gauß (reell)" liegen kann.

• Für zweidimensionale Verfahren wie QAM und mehrstufige PSK gilt dagegen die Grenzkurve "Gauß (komplex)", die hier gestrichelt gezeichnet ist und stets links von der durchgezogenen Kurve liegt.
• Näheres hierzu finden Sie im Abschnitt  Maximale Coderate für QAM–Strukturen  des Buches "Informationstheorie".
  
• Auch diese Grenzkurve wurde mit QAM–Verfahren und sehr langen Kanalcodes inzwischen nahezu erreicht, ohne dass sie jemals überschritten werden wird.

Aufgaben zum Kapitel

Aufgabe 1.17: Zum Kanalcodierungstheorem

Aufgabe 1.17Z: BPSK–Kanalkapazität