Entire GSM Transmission System

Voice and data transmission components

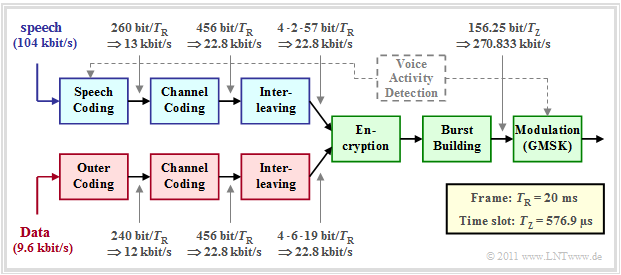
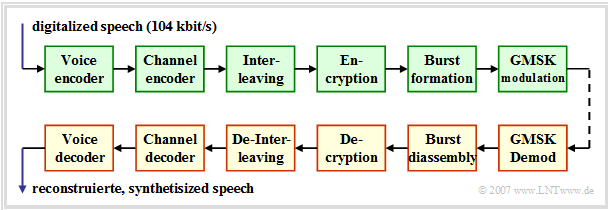
Below you can see the block diagram of the GSM transmission system at the transmitting end, which is

is suitable for both digitized voice signals $($sampling rate: $8 \ \rm kHz$, quantization: $13$ bit ⇒ data rate: $104 \ \rm kbit/s)$
as well as being suitable for $9.6 \ \rm kbit/s$ data signals.

Components for voice are shown in blue, those for data in red, and common blocks in green.

Components of the voice and data communication with GSM

Here is a brief description of each component:

Speech signals are compressed by voice coding from $104 \ \rm kbit/s$ to $13 \ \rm kbit/s$ - i.e. by a factor $8$. The bit rate given in the graph is for the full rate codec, which delivers $($duration $T_{\rm R} = 20\ \rm ms)$ exactly $260$ bits per speech frame.
The AMR codec delivers in highest mode $12.2 \ \rm kbit/s$ $(244$ bits per speech frame$)$. However, the speech codec must also transmit additional information regarding the current mode, so the data rate before channel coding is also $13 \rm kbit/s$ .
The task of the dashed Voice Activity Detection' is to decide whether the current voice frame actually contains a voice signal or just a voice pause during which the power of the transmit amplifier should be turned down.
By channel coding redundancy is added again to allow error correction at the receiver. Per voice frame, the channel encoder outputs $456$ bits, resulting in the data rate $22.8 \ \rm kbit/s$ . The more important bits are specially protected.
The interleaver scrambles the resulting bit sequence to reduce the influence of bundle errors. The $456$ input bits are split into four time frames of $114$ bits each. Thus, two consecutive bits are always transmitted in two different bursts.
A data channel - marked in red in the figure - differs from a voice channel (marked in blue) only by the different input rate $(9.6 \ \rm kbit/s$ instead of $104 \ \rm kbit/s)$ and the use of a second, outer channel encoder instead of the voice encoder.

The components highlighted in green apply equally to voice and data transmission. The first common system component for voice and data transmission in the block diagram of the GSM transmitter is the encryption, which is intended to prevent unauthorized persons from gaining access to the data.

There are two fundamentally different encryption methods:

Symmetric encryption: This knows only one secret key, which is used both for encrypting and enciphering the messages in the sender and for decrypting and deciphering them in the receiver. The key must be generated prior to communication and exchanged between the communication partners via a secure channel. The advantage of this encryption method used in conventional GSM is that it works very quickly.
Asymmetric encryption: This method uses two independent but matching asymmetric keys. It is not possible to use one key to calculate the other. The "Public Key" is publicly available and is used for encryption. The "Private Key" is secret and used for decryption. In contrast to the symmetric encryption methods, the asymmetric methods are much slower, but also offer higher security.

The second green block is the bursting, where there are different burst types. In Normal Burst the $114$ encoded, scrambled and encrypted bits are mapped to $156.25$ bits by adding Guard Period, signaling bits, etc. These are transmitted within a time slot of duration $T_{\rm Z} = 576.9 \rm µ s$ by means of the modulation method "GMSK". This results in the gross data rate $270.833 \ \rm kbit/s$.

At the receiver there are in reverse order the blocks

Demodulation,
burst decomposition,
decryption,
de-interleaving,
channel decoding,
voice decoding.

On the next pages all blocks of the above transmission scheme are presented in detail.

Coding for voice signals

Uncodierte Funkdatenübertragung führt zu Bitfehlerraten im Prozentbereich. Mit Channel Coding können aber manche Übertragungsfehler beim Empfänger erkannt oder sogar korrigiert werden. Die Bitfehlerrate lässt sich so auf Werte kleiner als $10^{–5}$ reduzieren.

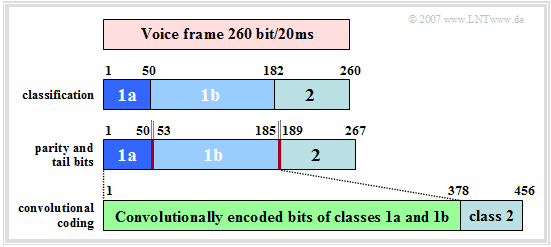
Zur Codierung von Sprachsignalen bei GSM

Zunächst betrachten wir die GSM-Kanalcodierung für die Sprachkanäle, wobei als Sprachcoder der "Vollraten–Codec" vorausgesetzt wird. Die Kanalcodierung eines Sprachrahmens von $20\ \rm ms$ Dauer erfolgt in vier aufeinander folgenden Schritten entsprechend der Grafik.
Aus der Beschreibung im Kapitel "Voice Coding" ist zu ersehen, dass nicht alle $260$ Bit den gleichen Einfluss auf die subjektiv empfundene Sprachqualität haben.

Deshalb werden die Daten entsprechend ihrer Wichtigkeit in drei Klassen aufgeteilt: Die $50$ wichtigsten Bit bilden die Klasse 1a, weitere $132$ werden der Klasse 1b zugeteilt und die restlichen $78$ Bit ergeben die eher unwichtige Klasse 2.
Im nächsten Schritt wird für die $50$ besonders wichtigen Bit der Klasse 1a mit einem rückgekoppelten Schieberegister eine drei Bit lange "Cyclic Redundancy Check" (CRC)–Prüfsumme berechnet. Das Generatorpolynom für diese CRC–Überprüfung lautet:

$$G_{\rm CRC}(D) = D^3 + D +1\hspace{0.05cm}. $$

Anschließend werden den insgesamt $185$ Bit der Klasse 1a und 1b inclusive den drei (rot eingezeichneten) CRC–Paritätsbits noch vier (gelbe) Tailbits „0000” angehängt. Diese vier Bit initialisieren die vier Speicherregister des nachfolgenden Faltungscoders jeweils mit $0$, so dass für jeden Sprachrahmen von einem definierten Status ausgegangen werden kann.
Der Faltungscode mit der Coderate $R_{\rm C} = 1/2$ verdoppelt diese $189$ wichtigsten Bit auf $378$ Bit und schützt diese somit signifikant gegen Übertragungsfehler. Anschließend werden noch die $78$ Bit der unwichtigeren Klasse 2 ungeschützt angehängt.
Auf diese Weise ergeben sich nach der Kanalcodierung pro $20 \ \rm ms$–Sprachrahmen genau $456$ Bit. Dies entspricht einer (codierten) Datenrate von $22.8\ \rm kbit/s$ gegenüber $13\ \rm kbit/s$ nach der Sprachcodierung. Die effektive Kanalcodierungsrate beträgt somit $260/456 = 57\%$.

Interleaving bei Sprachsignalen

Das Ergebnis der Faltungsdecodierung hängt nicht nur von der Häufigkeit der Übertragungsfehler ab, sondern auch von deren Verteilung. Um gute Korrekturergebnisse zu erzielen, sollte der Kanal kein Gedächtnis besitzen, sondern möglichst statistisch unabhängige Bitfehler liefern.

Bei Mobilfunksystemen treten Übertragungsfehler aber meist in Blöcken (Error Bursts) auf. Durch den Einsatz der Interleaving–Technik werden solche Bündelfehler über mehrere Bursts gleichmäßig verteilt und so deren Auswirkungen abgeschwächt.

Interleaving bei GSM–Sprachsignalen

Bei einem Sprachkanal arbeitet der Interleaver in folgender Weise:

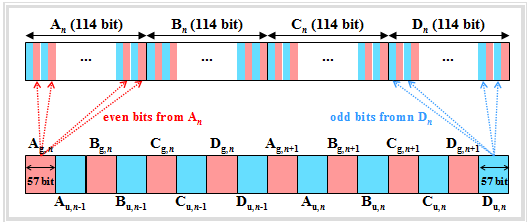
Die $456$ Eingangsbit pro Sprachrahmen werden nach einem festen Algorithmus auf vier Blöcke zu je $114$ Bit aufgeteilt. Wir bezeichnen diese für den $n$–ten Sprachrahmen mit $A_n$, $B_n$, $C_n$ und $D_n$. Der Index $n-1$ bezeichnet den vorhergehenden Rahmen und $n+1$ den nachfolgenden.
Der Block $A_n$ wird weiterhin in zwei Unterblöcke $A_{{\rm g},\hspace{0.05cm}n}$ und $A_{{\rm u},\hspace{0.05cm}n}$ zu je $57$ Bit unterteilt, wobei $A_{{\rm g},\hspace{0.05cm}n}$ nur die geraden Bitpositionen und $A_{{\rm u},\hspace{0.05cm}n}$ die ungeraden Bitpositionen von $A_n$ bezeichnen. In der Grafik sind $A_{{\rm g},\hspace{0.05cm}n}$ und $A_{{\rm u},\hspace{0.05cm}n}$ an der roten bzw. blauen Hinterlegung zu erkennen.
Der Unterblock $A_{{\rm g},\hspace{0.05cm}n}$ des $n$–ten Sprachrahmens wird mit dem Block $A_{{\rm u},\hspace{0.05cm}n-1}$ des vorherigen Rahmens zusammengefügt und ergibt die $114$ Nutzdaten eines Normal Bursts: $\left (A_{{\rm g},\hspace{0.05cm}n}, A_{{\rm u},\hspace{0.05cm}n-1}\right )$. Gleiches gilt für die drei nächsten Bursts: $\left (B_{{\rm g},\hspace{0.05cm}n}, B_{{\rm u},\hspace{0.05cm}n-1}\right )$, $\left (C_{{\rm g},\hspace{0.05cm}n}, C_{{\rm u},\hspace{0.05cm}n-1}\right )$, $\left (D_{{\rm g},\hspace{0.05cm}n}, D_{{\rm u},\hspace{0.05cm}n-1}\right )$.
In gleicher Weise werden die ungeraden Unterblöcke des $n$–ten Sprachrahmens mit den geraden Unterblöcken des nachfolgenden Rahmens verschachtelt: $\left (A_{{\rm g},\hspace{0.05cm}n+1}, A_{{\rm u},\hspace{0.05cm}n}\right )$, ... , $\left (D_{{\rm g},\hspace{0.05cm}n+1}, D_{{\rm u},\hspace{0.05cm}n}\right )$.

$\text{Fazit:}$ Die hier beschriebene Verwürfelungsart wird block-diagonales Interleaving genannt, hier speziell vom Grad $8$:

Dieses vermindert die Störanfälligkeit gegenüber Bündelfehlern.
So werden niemals zwei aufeinander folgende Bit eines Datenblocks direkt hintereinander gesendet.
Mehrbitfehler treten nach dem De–Interleaver isoliert auf und können so wirkungsvoller korrigiert werden.

Codierung und Interleaving bei Datensignalen

Für die GSM–Datenübertragung steht jedem Teilnehmer lediglich eine Nettodatenrate von $9.6\ \rm kbit/s$ zur Verfügung. Zur Fehlersicherung werden zwei Verfahren eingesetzt:

Forward Error Correction (FEC, deutsch: Vorwärtsfehlerkorrektur) wird auf der physikalischen Schicht durch Anwendung von Faltungscodes realisiert.
Automatic Repeat Request (ARQ); dabei werden auf der Sicherungsschicht defekte und nicht korrigierbare Pakete neu angefordert.

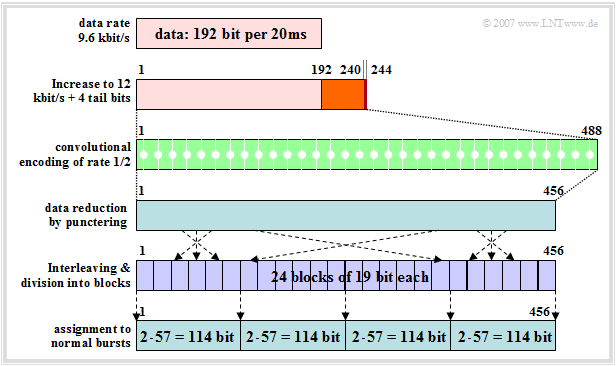
Zur Verdeutlichung von Codierung und Interleaving bei Datensignalen

Die Grafik verdeutlicht Kanalcodierung und Interleaving für den Datenkanal mit $9.6\ \rm kbit/s$, die im Gegensatz zur Kanalcodierung des Sprachkanals $($mit Bitfehlerrate $10^{–5}$... $10^{–6})$ eine nahezu fehlerfreie Rekonstruktion der Daten erlaubt:

Die Datenbitrate von $9.6\ \rm kbit/s$ wird zuerst im Terminal Equipment der Mobilstation durch eine nicht GSM–spezifische Kanalcodierung um $25\%$ auf $12\ \rm kbit/s$ erhöht, um eine Fehlererkennung in leitungsvermittelten Netzen zu ermöglichen.
Bei der Datenübertragung sind alle Bit gleichwertig, so dass es im Gegensatz zur Codierung des Sprachkanals keine Klassen gibt. Die $240$ Bit pro $20 \ \rm ms$–Zeitrahmen werden zusammen mit vier Tailbits $0000$ zu einem einzigen Datenrahmen zusammengefasst.
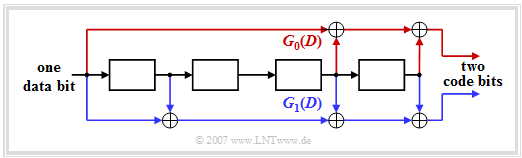
Diese $244$ Bit werden wie bei Sprachkanälen durch einen Faltungscoder der Rate $1/2$ auf $488$ Bit verdoppelt. Pro einlaufendem Bit werden zwei Codesymbole erzeugt, zum Beispiel gemäß den Generatorpolynomen $G_0(D) = 1 + D^3 + D^4$ und $G_1(D) = 1 + D + D^3 + D^4$:

Bei GSM verwendeter Faltungscoder der Rate $1/2$

Der nachfolgende Interleaver erwartet – ebenso wie ein „Sprach–Interleaver” – als Eingabe nur $456$ Bit pro Rahmen. Deshalb werden von den $488$ Bit am Ausgang des Faltungscodierers noch $32$ Bit an den Positionen $15 · j - 4 \ ( j = 1$, ... ,$ 32 )$ entfernt („Punktierung”).
Da die Datenübertragung weniger zeitkritisch ist als die Sprachübertragung, wird hier ein höherer Interleaving–Grad gewählt. Die $456$ Bit werden auf bis zu $24$ Interleaver–Blöcke zu je $19$ Bit verteilt, was bei Sprachdiensten aus Gründen der Echtzeitübertragung nicht möglich wäre.
Danach werden die $456$ Bit auf vier aufeinander folgende Normal Bursts aufgeteilt und versandt. Beim Einpacken in die Bursts werden wieder Gruppierungen gerader und ungerader Bits gebildet, ähnlich dem Interleaving im Sprachkanal.

Empfängerseite der GSM–Strecke – Decodierung

Der GSM–Empfänger (gelb hinterlegt) beinhaltet die GMSK-Demodulation, die Burstzerlegung, die Entschlüsselung, das De–Interleaving sowie die Kanal– und Sprachdecodierung.

Empfängerseitige Datenverarbeitung bei GSM

Zu den beiden letzten Blöcken in obigem Bild ist anzumerken:

Das Decodierverfahren wird durch die GSM–Spezifikation nicht vorgeschrieben, sondern ist den einzelnen Netzbetreibern überlassen. Die Leistungsfähigkeit ist vom eingesetzten Algorithmus zur Fehlerkorrektur abhängig.
Zum Beispiel wird beim Decodierverfahren Maximum Likelihood Sequence Estimation (MLSE) die wahrscheinlichste Bitsequenz unter Verwendung des Viterbi–Algorithmus oder eines MAP–Empfängers (Maximum A–posteriori Probability) ermittelt.
Nach der Fehlerkorrektur wird der Cyclic Redundancy Check (CRC) durchgeführt, wobei beim Vollraten–Codec der Grad des verwendeten CRC–Generatorpolynoms $G= 3$ ist. Damit werden alle Fehlermuster bis zum Gewicht $3$ und alle Bündelfehler bis zur Länge $4$ erkannt.
Anhand des CRC wird über die Verwendbarkeit eines jeden Sprachrahmens entschieden. Ist das Testergebnis positiv, so werden im nachfolgenden Sprachdecoder aus den Sprachparametern $(260$ Bit pro Rahmen$)$ die Sprachsignale synthetisiert.
Sind Rahmen ausgefallen, so werden die Parameter früherer, als korrekt erkannter Rahmen zur Interpolation verwendet ⇒ Fehlerverschleierung. Treten mehrere nicht korrekte Sprachrahmen in Folge auf, so wird die Leistung kontinuierlich bis hin zur Stummschaltung abgesenkt.

Aufgabe zum Kapitel

Aufgabe 3.7: Komponenten des GSM–Systems