Speech Coding

1. Examples of Communication Systems
2. GSM – Global System for Mobile Communications
3. Speech Coding

• Previous page
• Next page

• Previous page
• Next page

Various speech coding methods

Each GSM subscriber has a maximum net data rate of  $\text{22.8 kbit/s}$  available,  while the ISDN fixed network operates with a data rate of  $\text{64 kbit/s}$  $($with  $8$  bit quantization$)$  or  $\text{104 kbit/s}$  $($with $13$ bit quantization$)$  respectively. 

• The task of  "speech coding"  $($"speech coding"$)$  KORREKTUR in GSM is to limit the amount of data for speech signal transmission to  $\text{22.8 kbit/s}$  and to reproduce the speech signal at the receiver side in the best possible way.

• The functions of the GSM encoder and the GSM decoder are usually combined in a single functional unit called  "codec".

Different signal processing methods are used for speech coding KORREKTUR: encoding? and decoding:

• The  »GSM Full Rate Vocoder«  was standardized in 1991 from a combination of three compression methods for the GSM radio channel.  It is based on  "Linear Predictive Coding"  $\rm (LPC)$  in conjunction with  "Long Term Prediction"  $\rm (LTP)$  and  "Regular Pulse Excitation"  $\rm (RPE)$.

• The  »GSM Half Rate Vocoder«  was introduced in 1994 and provides the ability to transmit speech at nearly the same quality in half a traffic channel  $($data rate  $\text{11.4 kbit/s})$.

• The  »Enhanced Full Rate Vocoder«  $\rm (EFR\ codec)$  was standardized and implemented in 1995,  originally for the North American DCS1900 network.  The EFR codec provides better voice quality compared to the conventional full rate codec.

• The  »Adaptive Multi Rate Codec«  $\rm (AMR\ codec)$  is the latest speech codec for GSM.  It was standardized in 1997 and also mandated in 1999 by the  "Third Generation Partnership Project" $\rm (3GPP)$  as the standard speech codec for third generation mobile systems such as UMTS.

• In contrast to conventional AMR,  where the speech signal is bandlimited to the frequency range from  $\text{300 Hz}$  to   $\text{3.4 kHz}$,  $\text{Wideband AMR}$,  which was developed and standardized for UMTS in 2007,  assumes a wideband signal   $\text{(50 Hz - 7 kHz)}$.  This is therefore also suitable for music signals.

⇒   You can visualize the quality of these speech coding schemes for speech and music with the  $($German language$)$  SWF applet 
               "Qualität verschiedener Sprach–Codecs"   ⇒   "Quality of different speech codecs".

GSM Full Rate Vocoder

LPC, LTP and RPE parameters in the GSM Full Rate Vocoder

Table of GSM full rate codec parameters

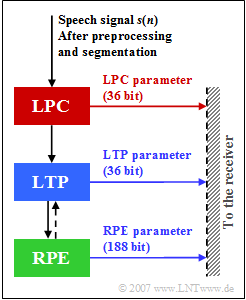
In the  »Full Rate Vocoder«,  the analog speech signal in the frequency range between  $300 \ \rm Hz$  and  $3400 \ \rm Hz$ 

• is first sampled with  $8 \ \rm kHz$  and

• then linearly quantized with  $13$  bits   ⇒   »A/D conversion«,

resulting in a data rate of  $104 \ \rm kbit/s$.

In this method,  speech coding is performed in four steps:

1. The preprocessing,
2. the setting of the short-term analyze filter  $($Linear Predictive Coding,  $\rm LPC)$,
3. the control of the Long Term Prediction  $\rm (LTP)$  filter,  and
4. the encoding of the residual signal by a sequence of pulses  $($Regular Pulse Excitation,  $\rm RPE)$.

In the upper graph,  $s(n)$  denotes the speech signal sampled and quantized at distance  $T_{\rm A} = 125\ \rm µ s$  after the continuously performed preprocessing,  where

• the digitized microphone signal is freed from a possibly existing DC signal component  $($"offset"$)$  in order to avoid a disturbing whistling tone of approx.  $2.6 \ \rm kHz$  during decoding when recovering the higher frequency components,  and

• additionally,  higher spectral components of  $s(n)$  are raised to improve the computational accuracy and effectiveness of the subsequent LPC analysis.

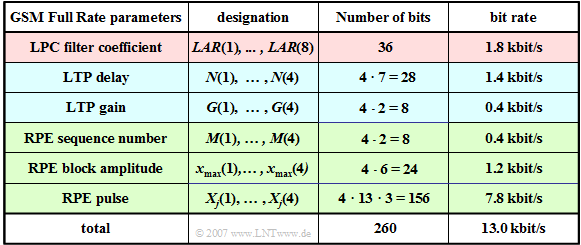
The table shows the  $76$  parameters  $(260$ bit$)$  of the functional units LPC, LTP and RPE.  The meaning of the individual quantities is described in detail on the following pages.

All processing steps  $($LPC, LTP, RPE$)$  are performed in blocks of  $20 \ \rm ms$  duration over  $160$  samples of the preprocessed speech signal,  which are called  »GSM speech frames« .

• In the full rate codec,  a total of  $260$ bits  are generated per speech frame,  resulting in a data rate of  $13\ \rm kbit/s$.

• This corresponds to a compression of the speech signal by a factor  $8$  $(104 \ \rm kbit/s$  related to  $13 \ \rm kbit/s)$.

Linear Predictive Coding

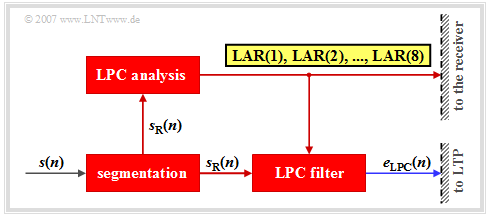
The block  »Linear Predictive Coding«  $\rm (LPC)$  performs short-time prediction, that is, it determines the statistical dependencies among the samples in a short range of one millisecond.  The following is a brief description of the LPC principle circuit:

Building blocks of GSM Linear Predictive Coding  $\rm (LPC)$

• First,  for this purpose  the time-unlimited signal  $s(n)$  is segmented into intervals  $s_{\rm R}(n)$  of  $20\ \rm ms$ duration  $(160$ samples$)$.  By convention,  the run variable within such a speech frame  $($German:  "Rahmen"   ⇒   subscript:  "R"$)$  can take the values  $n = 1$, ... , $160$.

• In the first step of  »LPC analysis«  dependencies between samples are quantified by the autocorrelation  $\rm ACF)$  coefficients with indices  $0 ≤ k ≤ 8$  :

$$φ_{\rm s}(k) = \text{E}\big [s_{\rm R}(n) · s_{\rm R}(n + k)\big ].$$

• From these nine ACF values,  using the so-called  "Schur recursion"  eight reflection coefficients  $r_{k}$  are calculated,  which serve as a basis for setting the coefficients of the LPC analysis filter for the current frame.

• The coefficients  $r_{k}$  have values between  $±1$.  Even small changes in  $r_{k}$  at the edge of their value range cause large changes for speech coding.  The eight reflectance values  $r_{k}$  are represented logarithmically   ⇒   »LAR parameters«  $($"Log Area Ratio"$)$:

$${\rm LAR}(k) = \ln \ \frac{1-r_k}{1+r_k}, \hspace{1cm} k = 1,\hspace{0.05cm} \text{...}\hspace{0.05cm} , 8.$$

• Then,  the eight LAR parameters are quantized by different bit numbers according to their subjective meaning,  encoded and made available for transmission. 

• The first two parameters are represented with six bits each, 
• the next two with five bits each, 
• $\rm LAR(5)$  and  $\rm LAR(6)$  with four bits each,  and
• the last two –   $\rm LAR(7)$  and  $\rm LAR(8)$–   with three bits each.

• If the transmission is error-free,  the original speech signal  $s(n)$  can be completely reconstructed again at the receiver from the eight LPC parameters  $($in total  $36$  bits$)$  with the corresponding LPC synthesis filter,  if one disregards the unavoidable additional quantization errors due to the digital description of the LAR coefficients.

• Further,  the prediction error signal  $e_{\rm LPC}(n)$  is obtained using the LPC filter.  This is also the input signal for the subsequent long-term prediction.  The LPC filter is not recursive and has only a short memory of about one millisecond.

LPC Prediction error signal at GSM  $($time–frequency representation$)$

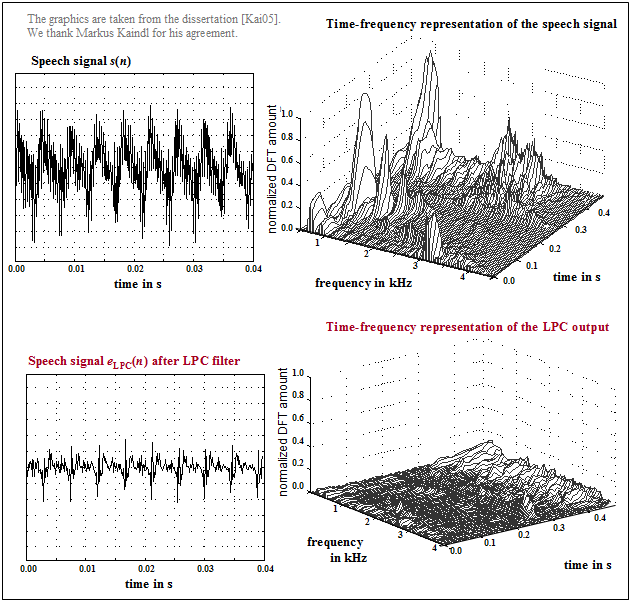
$\text{Example 1:}$  The graph from  [Kai05]  shows

• top left:  a section of the speech signal  $s(n)$, 

• top right:  its time-frequency representation,

• bottom left:  the LPC prediction error signal  $e_{\rm LPC}(n)$,

• bottom right:  its time-frequency representation.

One can see from these pictures

1. the smaller amplitude of  $e_{\rm LPC}(n)$  compared to  $s(n)$,
2. the significantly reduced dynamic range,  and
3. the flatter spectrum of the remaining signal.

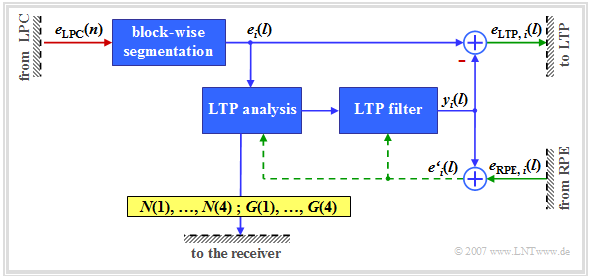
Long Term Prediction

The block  »Long Term Prediction«  $\rm (LTP)$  exploits the property of the speech signal that it also has periodic structures  $($voiced sections$)$.  This fact is used to reduce the redundancy present in the signal.

Blocks of GSM Long Term Prediction  $\rm (LTP)$

• The long-term prediction  $($(LTP analysis and filtering$)$  is performed four times per speech frame,  i.e. every  $5 \rm ms$.

• The four subblocks consist of  $40$  samples each and are numbered by  $i = 1$, ... , $4$.

The following is a short description according to the shown LTP schematic diagram – see  [Kai05].

1. The LTP input signal is the output signal  $e_{\rm LPC}(n)$  of the short-term prediction.  The signals after segmentation into four subblocks are denoted by  $e_i(l)$  where each  $l = 1,\ 2$, ... , $40$.
2. For this analysis,  the cross-correlation function  $φ_{ee\hspace{0.03cm}',\hspace{0.05cm}i}(k)$  of the subblock  $i$  of the LPC predictor error signal  $e_i(l)$  with the reconstructed LPC residual signal  $e\hspace{0.03cm}'_i(l)$  from the three previous subframes.
3. The memory of this LTP predictor is  $5 \ \rm ms$  ...  $15 \ \rm ms$  and thus significantly longer than that of the LPC predictor  $(1 \ \rm ms)$.
4. $e\hspace{0.03cm}'_i(l)$  is the sum of the LTP filter output signal  $y_i(l)$  and the correction signal  $e_{\rm RPE,\hspace{0.05cm}i}(l)$ provided by the following component  $($"Regular Pulse Excitation"$)$  for the  $i$-th subblock.
5. The  $k$  value for which the cross-correlation function  $φ_{ee\hspace{0.03cm}',\hspace{0.05cm}i}(k)$  becomes maximum determines the optimal LTP delay  $N(i)$  for each subblock  $i$. 
6. The delays  $N(1)$  to  $N(4)$  are each quantized to seven bits and made available for transmission.
7. The gain factor  $G(i)$  associated with  $N(i)$  – also called  "LTP gain"  – is determined so that the subblock found at the location  $N(i)$  after multiplication by  $G(i)$  best matches the current subframe  $e_i(l)$.
8. The gains  $G(1)$,  ... ,  $G(4)$  are each quantized by two bits and together with  $N(1)$, ... , $N(4)$  give the  $36$  bits for the eight LTP parameters.
9. The signal  $y_i(l)$  after LTP analysis and filtering is an estimated signal for the LPC signal  $e_i(l)$  in  $i$-th subblock.
10. The difference between the two signals gives the LTP residual signal  $e_{ {\rm LTP},\hspace{0.05cm}i}(l)$,  which is passed on to the next functional unit  "RPE".

LTP prediction error signal at GSM (time–frequency representation)

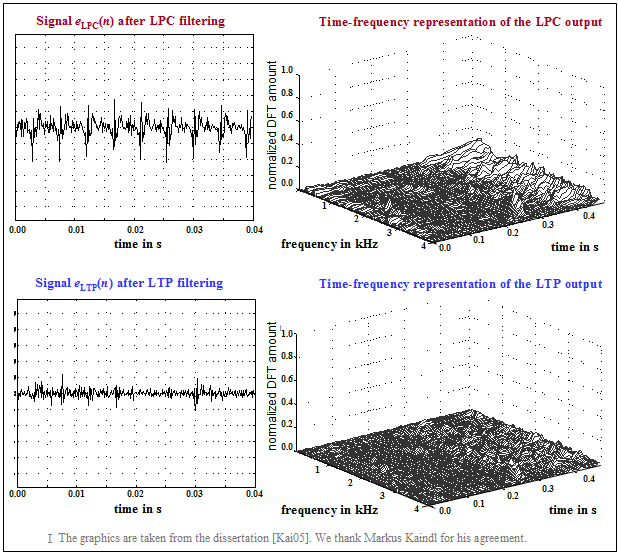
$\text{Example 2:}$  The graph from  [Kai05]  shows

• top left:  a section of the LPC prediction error signal  $e_{\rm LPC}(n)$  – simultaneously the LTP input signal,

• top right:  its time-frequency representation,

• bottom left:  the the residual error signal  $e_{\rm LTP}(n)$  after long-term prediction,

• bottom right:  its time-frequency representation.

Only one subblock is considered.  Therefore,  the same letter  $n$  is used here for the discrete time in LPC and LTP.

One can see from these representations:

1. The smaller amplitudes of  $e_{\rm LTP}(n)$  compared to  $e_{\rm LPC}(n)$;
2. the significantly reduced dynamic range of  $e_{\rm LTP}(n)$,  especially in periodic  $($i.e. voiced$)$  sections;
3. in the frequency domain,  a reduction of the prediction error signal due to LTP is also evident.

Regular Pulse Excitation – RPE Coding

The signal after LPC and LTP filtering is already redundancy–reduced,  i.e.  it requires a lower bit rate than the sampled speech signal  $s(n)$.

Building blocks of Regular Pulse Excitation  $\rm (RPE)$  in GSM

• In the following functional unit  »Regular Pulse Excitation«  $\rm (RPE)$  the irrelevance is further reduced.

• This means that signal components that are less important for the subjective hearing impression are removed.

It should be noted with regard to this block diagram:

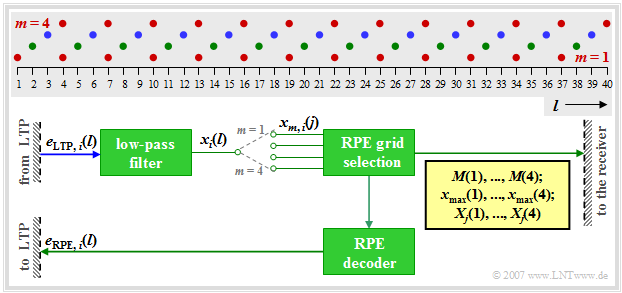
• RPE coding is performed for  $5 \rm ms$ subframes  $(40$  samples$)$.  This is indicated by the index  $i$  in the input signal  $e_{{\rm LTP},\hspace{0.03cm} i}(l)$  where with  $i = 1, 2, 3, 4$  again the individual subblocks are numbered.

• In the first step,  the LTP prediction error signal  $e_{{\rm LTP}, \hspace{0.03cm}i}(l)$  is bandlimited by a low-pass filter to about one third of the original bandwidth – i.e. to  $1.3 \rm kHz$. 

• In a second step,  this enables a reduction of the sampling rate by a factor of about  $3$.

• So the output signal  $x_i(l)$  is decomposed with  $l = 1$, ... , $40$  by subsampling into four subsequences  $x_{m, \hspace{0.03cm} i}(j)$  with  $m = 1$, ... , $4$  and  $j = 1$, ... , $13$. 

• The subsequences  $x_{m,\hspace{0.08cm} i}(j)$  include the following samples of the signal  $x_i(l)$:

1.   $m = 1$:   $l = 1, \ 4, \ 7$, ... , $34, \ 37$  $($red dots$)$,
2.   $m = 2$:   $l = 2, \ 5, \ 8$, ... , $35, \ 38$  $($green dots$)$,
3.   $m = 3$:   $l = 3, \ 6, \ 9$, ... , $36, \ 39$  $($blue dots$)$,
4.   $m = 4$:   $l = 4, \ 7, \ 10$, ... , $37, \ 40$  $($also red,  largely identical to  $m = 1)$.

• For each subblock  $i$  in the block  "RPE Grid Selection"  the subsequence  $x_{m,\hspace{0.03cm}i}(j)$  with the highest energy is selected.  The index  $M_i$  of this  "optimal sequence"  is quantized with two bits and transmitted as  $\mathbf{\it M}(i)$.  In total,  the four RPE subsequence indices require  $\mathbf{\it M}(1)$, ... ,  $\mathbf{\it M}(4)$  thus eight bits.

• From the optimal subsequence for subblock  $i$  $($with index  $M_i)$  the  amplitude maximum  $x_{\rm max,\hspace{0.03cm}i}$  is determined.  This value is logarithmically quantized with six bits and made available for transmission as  $\mathbf{{\it x}_{\rm max}}(i)$.  In total,  the four RPE block amplitudes require  $24$  bits.

• In addition,  for each subblock  $i$  the optimal subsequence is normalised to  $x_{{\rm max},\hspace{0.03cm}i}$.  The obtained  $13$  samples are then quantized with three bits each and transmitted encoded as  $\mathbf{\it X}_j(i)$.  The  $4 \cdot 13 \cdot 3 = 156$  bits describe the so-called  »RPE pulse«.

• Then these RPE parameters are decoded locally again and fed back as a signal  $e_{{\rm RPE},\hspace{0.03cm}i}(l)$  to the LTP synthesis filter in the previous subblock,  from which,  together with the LTP estimation signal  $y_i(l)$  the signal  $e\hspace{0.03cm}'_i(l)$  is generated  (see  $\rm LTP graph$).

• By interposing two zero values between each two transmitted RPE samples,  the baseband from zero to  $1300 \ \rm Hz$  in the range from  $1300 \ \rm Hz$  to  $2600 \ \ \rm Hz$  in sweep position and from  $2600 \ \ \rm Hz$  to  $3900 \ \rm Hz$  in normal position.

• This is the reason for the necessary DC signal release in the preprocessing.  Otherwise,  a disturbing whistling tone at  $2.6 \ \rm kHz$ would result from the described convolution operation.

Half Rate Vocoder and Enhanced Full Rate Codec

After the standardization of the full rate codec in 1991,  the subsequent focus was on the development of new speech codecs with two specific objectives,  namely

• the better utilisation of the bandwidth available in GSM systems,  and

• the improvement of voice quality.

This development can be summarised as follows:

1. By 1994, a new process was developed with the  »Half Rate Vocoder«.  This has a data rate of $5.6\ \rm kbit/s$  and thus offers the possibility of transmitting speech in half a traffic channel with approximately the same quality.  This allows two calls to be handled simultaneously on one time slot.  However,  the half rate codec was only used by mobile phone operators when a radio cell was congested.  In the meantime,  the half rate codec no longer plays a role.
   
   
2. In order to further improve the voice quality, the  »Enhanced Full Rate Codec«  $\rm(EFR$  codec$)$  was introduced in 1995.  This speech coding method – originally developed for the US American DCS1900 network – is a full rate codec with the  $($slightly lower$)$  data rate  $12.2 \ \rm kbit/s$.  The use of this codec must of course be supported by the mobile phone.
   
   
3. Instead of the  $\rm RPE – LPT$   $($"regular pulse excitation - long term prediction"$)$  compression of the conventional full rate codec,  this further development also uses  »Algebraic Code Excitation Linear Prediction«,  which offers a significantly better speech quality and also improved error detection and concealment.  More information about this can be found on the page after next.

Adaptive Multi Rate Codec

The GSM codecs described so far always work with a fixed data rate with regard to speech and channel coding,  regardless of the channel conditions and the network load.

In 1997,  a new adaptive speech coding method for mobile radio systems was developed and shortly afterwards standardised by the  "European Telecommunications Standards Institute"  $\rm (ETSI)$  according to proposals of the companies Ericsson,  Nokia and Siemens.

The Chair of Communications Engineering of the Technical University of Munich,  which provides this learning tutorial  "LNTwww",  was decisively involved in the research work on the system proposal of Siemens AG.  For more details,  see  [Hin02].

The  »Adaptive Multi Rate Codec«  $\rm (AMR)$  has the following properties:

1. It adapts flexibly to the current channel conditions and to the network load by operating either in full rate mode  $($higher voice quality$)$  or in half rate mode  $($lower data rate$)$.  In addition,  there are several intermediate stages.
2. It offers improved voice quality in both full rate and half rate traffic channels,  due to the flexible division of the available gross channel data rate between speech and channel coding.
3. It has greater robustness against channel errors than the codecs from the early days of mobile radio technology.  This is especially true when used in the full rate traffic channel.

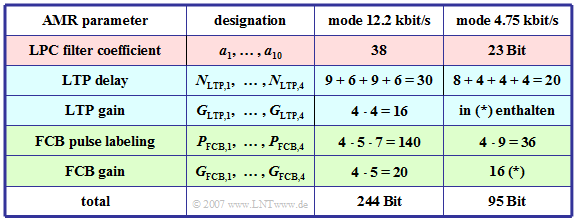
The AMR codec provides  »eight different modes«  with data rates between  $12.2 \ \rm kbit/s$  $(244$  bits per frame of  $20 \ \rm ms)$  and  $4.75 \ \rm kbit/s$  $(95$ bits per frame$)$.

Three modes play a prominent role,  namely

• $12.2 \ \rm kbit/s$  – the enhanced GSM full rate  $\rm EFR)$  codec,

• $7.4 \rm kbit/s$  – the speech compression according to the US standard  "IS-641",  and

• $6.7 \rm kbit/s$  – the EFR speech transmission of the Japanese PDC mobile radio standard.

Compilation of AMR parameters Korrektur Hochkomma, enthalten

The following descriptions mostly refer to the mode with  $12.2 \ \rm kbit/s$:

• All earlier methods of the AMR are based on minimizing the prediction error signal by forward prediction in the substeps LPC, LTP,  and RPE.

• In contrast,  the AMR codec uses a backward prediction according to the principle of  "analysis by synthesis".  This encoding principle is also called  »Algebraic Code Excited Linear Prediction«  $\rm (ACELP)$.

In the table, the parameters of the AMR codec are compiled for two modes:

•   $244$  bits per  $20 \ \rm ms$   ⇒   "mode  $12.2 \ \rm kbit/s$",

•   $95$  Bit per  $20 \ \rm ms$   ⇒   mode  "$4.75 \ \rm kbit/s$".

Algebraic Code Excited Linear Prediction

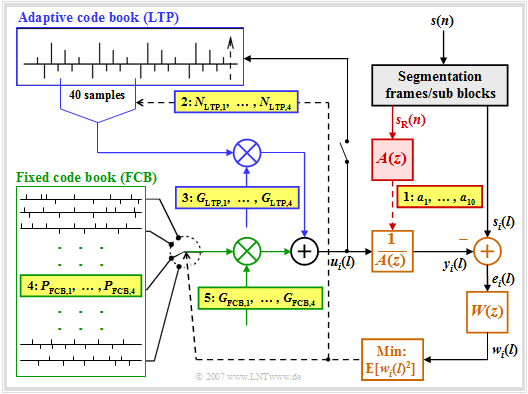
The graphic shows the  »AMR codec«  based on  $\rm ACELP$.  A short description of the principle follows.  A detailed description can be found for example in [Kai05]  .

Algebraic Code Excited Linear Prediction – Principle

• The speech signal  $s(n)$,  sampled at  $8 \ \rm kHz$  and quantized at  $13$  bits as in the GSM full rate codec,  is before further processing segmented into

1. frames  $s_{\rm R}(n)$  with  $n = 1$, ... , $160$,  and
2. subblocks  $s_i(l)$  with  $i = 1,\ 2,\ 3, 4$  and  $l = 1$, ... , $40$.

• The calculation of the LPC coefficients is done in the red highlighted block frame by frame every  $20 \ \rm ms$  corresponding to  $160$  samples,  since within this short time the spectral envelope of the signal  $s_{\rm R}(n)$  can be considered constant.

• For LPC analysis,  a filter  $A(z)$  of order  $10$  is usually chosen.  In the highest-rate mode with  $12.2 \ \rm kbit/s$,  the current coefficients  $a_k \ ( k = 1$, ... , $10)$  of the short-time prediction are quantized every  $10\ \rm ms$,  encoded and made available for transmission at point 1 highlighted in yellow.

• The further steps of the AMR are carried out every  $5 \ \rm ms$  according to the  $40$  samples of the signals  $s_i(l)$.  The long-term prediction  $\rm (LTP)$  – in the graphic outlined in blue – is realized here as an adaptive code book in which the samples of the preceding subblocks are entered.

• For the long-term prediction,  first the gain  $G_{\rm FCB}$  for the  "fixed code book"  $\rm (FCB)$  is set to zero,  so that a sequence of  $40$  samples of the adaptive code book are present at the input  $u_i(l)$  of the speech tract filter  $A(z)^{-1}$  set by the LPC.  The index  $i$  denotes the subblock under consideration.

• By varying the long-term prediction parameters  $N_{{\rm LTP},\hspace{0.05cm}i}$  and  $G_{{\rm LTP},\hspace{0.05cm}i}$  shall be achieved for this  $i$-th subblock that the mean power of the weighted error signal  $w_i(l)$  becomes minimal.

• The error signal  $w_i(l)$  is equal to the difference between the current speech frame  $s_i(l)$  and the output signal  $y_i(l)$  of the speech tract filter when excited with  $u_i(l)$,  taking into account the weighting filter  $W(z)$  to match the spectral characteristics of human hearing.

• In other words:  $W(z)$  removes those spectral components in the signal  $e_i(l)$  that are not perceived by an  "average ear".  In the  $12.2 \ \rm kbit/s$  mode one uses for the weighting filter  $W(z) = A(z/γ_1)/A(z/γ_2)$  with constant factors  $γ_1 = 0.9$  and  $γ_2 = 0.6$.

• For each subblock,  $N_{{\rm LTP},\hspace{0.05cm}i}$  denotes the best possible LTP delay,  which together with the LTP gain  $G_{{\rm LTP},\hspace{0.05cm}i}$  after averaging with respect to   $l = 1$, ... , $40$   minimizes the squared error  $\text{E}[w_i(l)^2]$.  In the graph dashed lines indicate control lines for iterative optimization.

• The described procedure is called  »analysis by synthesis«.  After a sufficiently large number of iterations,  the subblock  $u_i(l)$  is included in the adaptive code book.  The determined LTP parameters  $N_{{\rm LTP},\hspace{0.05cm}i}$  and  $G_{{\rm LTP},\hspace{0.05cm}i}$  are encoded and made available for transmission.

Fixed Code Book – FCB

After determining the best adaptive excitation,  a search is made for the best entry in the fixed code book  $\rm (FCB)$.

• This provides the most important information about the speech signal.

• For example,  in the $12.2 \ \rm kbit/s$  mode,  $40$ bits are derived from this per subblock.

• Thus,  in each frame of  $20$  milliseconds:     $160/244 ≈ 65\%$  of the encoding goes back to the block outlined in green in the graph on the last page.

The principle can be described in a few key points using the diagram as follows:

Track division at ACELP speech codec

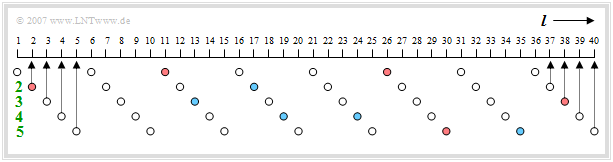
1. In the fixed code book,  each entry denotes a pulse where exactly  $10$  of  $40$  positions are occupied by  $+1$  resp.  $-1$.
2. According to the diagram, this is achieved by five tracks with eight positions each, of which exactly two have the values  $±1$  and all others are zero.
3. A red circle in the diagram  $($at positions  $2,\ 11,\ 26,\ 30,\ 38)$  indicates  "$+1$"  and a blue one  "$-1$"  $($in the example at the positions  $13,\ 17,\ 19,\ 24,\ 35)$.
4. In each track,  the two occupied positions are encoded with only three bits each  $($there are only eight possible positions$)$.
5. Another bit is used for the sign,  which defines the sign of the first–mentioned pulse.
6. If the pulse position of the second pulse is greater than that of the first, the second pulse has the same sign as the first, otherwise the opposite.
7. In the first track of our example,  there are positive pulses at position  $2 \ (010)$  and position  $5 \ (101)$,  where the position count starts at  $0$.  This track is thus marked by positions  "$010$"  and  "$101$"  and sign  "$1$"  $($positive$)$.
8. The marking for the second track is:   Positions  "$011$"  and  "$000$", sign  "$0$".  Since here the pulses at position  $0$  and  $3$  have different signs,  "$011$"  precedes  "$000$".  The sign "$0$"  $($negative$)$  refers to the pulse at the first–mentioned position  $3$.
9. Each impulse comb   consisting of  $40$  pulses, of which however  $30$  have the weight "zero"   results in a stochastic,   noise-like acoustic signal,  which after amplification with  $G_{{\rm LTP},\hspace{0.05cm}i}$  and shaping by the LPC speech filter  $A(z)^{-1}$  approximates the speech frame  $s_i(l)$.

Exercises for the chapter

Exercise 3.5: GSM Full Rate Vocoder

Exercise 3.6: Adaptive Multi Rate Codec