Contents
OVERVIEW OF THE FIRST MAIN CHAPTER
This first chapter serves as an introduction to the whole topic, which is covered by the nine books of the series $\rm LNTww$ .
This chapter describes in detail:
- the tasks and the basic structure of a message transmission system,
- the main functional units (source, transmitter, channel, receiver and sink) of such a system, and finally
- a classification of the signals occurring in a message system according to several evaluation criteria: deterministic or stochastic, energy or power limited, continuous or discrete time, continuous or discrete value, analog or digital.
At the end of the chapter follows a short summary about the Calculating with complex numbers.
Message - Information - Signal
One distinguishes basically between the terms „message” and „information”, which are often used synonymously nowadays.
$\text{Example 1:}$ An email from Mr. Maier to Mrs. Müller is always a message. For Mrs. Müller, however, receiving this email only means an information gain if she learns something new. The information transmitted by a message therefore depends to a great extent on the knowledge level of the recipient. In practice, the information contained in a message is rather small, especially in the field of telephony.
The transmission and storage of a message always requires an energetic or material carrier called signal . Physically the representation of a message is done by signals, which can be of very different nature.
Possible appearances are:
- electrical signals (for example current and voltage curve),
- electromagnetic waves (for example in radio transmission),
- Progression of pressure, temperature or other physical quantities,
- acoustic signals (for example, output signal of a loudspeaker),
- optical signals (for example output signal of a laser).
$\text{Please note:}$
- The signals used for message transmission are usually time functions. This means that (at least) one of the signal parameters is dependent on the time parameter $t$ . Such signal parameters are for example for a signal tone the amplitude ("volume") and the frequency ("pitch").
- In a message memory the time functions are often also mapped to spatial functions of suitable physical quantities such as magnetization (magnetic band) or degree of blackening (film).
The set of all message signals can be cataloged by different criteria, as described in chapter Klassifizierung von Signalen angegeben.
Block diagram of a message transmission system
In the following diagram a message transmission system is shown schematically.
The individual system components have the following tasks:
- The message source returns the source signal $q(t)$, which shall be transmitted over the message channel to the spatially distant sink. The message source can be for example a computer, a radio station or a telephone participant.
- In most cases the source signal $q(t)$ itself is unsuitable for transmission and must first be converted into the signal $s(t)$ in a suitable manner. This process is called „modulation” and is performed by the transmitter . Therefore $s(t)$ is called the transmit signal in the following.
- At transmission over the channel this signal $s(t)$ is changed in its form; at the same time more or less strong noise– and noise signals are added. The signal at the channel output and simultaneously at the receiver input is called the receive signal $r(t)$.
- The receiver must undo the conversion made by the sender. If, for example, the low-frequency source signal $q(t)$ was converted to the higher-frequency transmitter signal $s(t)$ the receiver must also contain a demodulator and undo this conversion.
- The last block in the model above is the message sink. The sink signal $v(t)$ is like the transmitted signal $q(t)$ again low frequency. In the ideal case, however, which in practice (due to the unavoidable noise) can never be reached exactly, should apply for all times $v(t) = q(t)$ .
Message source
As examples for news sources or for the source signal $q(t)$ can be mentioned
- Audio signals, for example speech or music,
- Video signals, for example an analog television signal or an MPEG encoded streaming video,
- Data signals, for example the data stream of a USB interface or an email on the Internet,
- Measure–signals, for example for control or regulation in a production process.
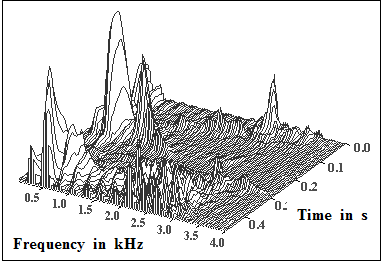
$\text{Example 2:}$ On the right you see the frequency-time representation of a speech signal.
- You can see the different frequency components in the kilohertz range at different times.
- By the way: This is a male speaker.
We thank Markus Kaindl [1], LNT/TUM, für die Bereitstellung der Grafik.
A distinction is made between analog and digital news sources. The forms of description presented in this book „Signal Representation” apply equally to analog and digital signals.
The basic differences between analog and digital signals are
- discussed in the chapter Classification of signals , and are clarified
- through the video Analoge und digitale Signale with examples.
Tasks of the transmitter
Wesentliche Aufgabe des Senders ist es, das Quellensignal $q(t)$ derart in ein Sendesignal $s(t)$ umzuformen, dass dieses unter Einhaltung vorgegebener Leistungsmerkmale möglichst gut an den Übertragungskanal angepasst ist. Dazu enthält jeder Sender entsprechende Funktionseinheiten wie
- Wandler – zum Beispiel ein Mikrofon zur Umwandlung der physikalischen Größe „Druck” (akustische Welle) in ein elektrisches Signal,
- Signalumsetzer – beispielsweise von „analog” nach „digital” mit Hilfe der Komponenten Abtastung, Quantisierung und Binärcodierung,
- Codierer zum Entfernen von Redundanz zur Datenkomprimierung (Quellencodierung) oder zum systematischen Hinzufügen von Redundanz, die beim Empfänger zur Fehlererkennung und/oder Fehlerkorrektur genutzt werden kann (Kanalcodierung),
- Modulator zur Anpassung an den Übertragungskanal – zum Beispiel eine Frequenzumsetzung mittels Amplituden-, Phasen- oder Frequenzmodulation bzw. den entsprechenden digitalen Verfahren ASK, PSK bzw. FSK.
Je nach Anwendung bedeuten die oben angesprochenen Leistungsmerkmale, dass für die Signalübertragung ganz spezifische Eigenschaften gefordert werden.
Solche Merkmale sind beispielsweise:
- Leistungsbegrenzung – aufgrund der Diskussionen zum Thema „Elektrosmog” hochaktuell,
- Bandbreiteneffizienz – die UMTS–Versteigerung im Jahr 2000 hat gezeigt, um welche Beträge es hierbei geht,
- Distanz bzw. Reichweite – ungünstige Werte erhöhen die Infrastrukturkosten,
- Übertragungsqualität – zum Beispiel ein hoher Signal–zu–Störabstand oder eine geringe Fehlerrate.
Übertragungskanal
Bei der Realisierbarkeit bestimmter Übertragungseigenschaften spielt das Übertragungsmedium mit seinen physikalischen Eigenschaften eine wesentliche Rolle.
Beispiele für Übertragungsmedien sind:
- elektrische Leitungen, zum Beispiel Kupferdraht, Twisted Pair,
- Koaxialkabel, zum Beispiel Antennenleitung oder Kabelnetz,
- Lichtwellenleiter, zum Beispiel Multimode- und Monomodeglasfaser,
- Funkkanäle, zum Beispiel Rundfunk, Mobilfunk und Satellitenfunk.
$\text{Bitte beachten Sie:}$ Diese Übertragungsmedien sind in der Praxis nicht ideal und beeinträchtigen die Übertragung.
Das bedeutet: Das Empfangssignal $r(t)$ unterscheidet sich vom Sendesignal $s(t)$, möglicherweise aufgrund
- der Kanaldämpfung,
- von Laufzeiten auf dem Kanal,
- von Verzerrungen linearer und nichtlinearer Art.
Hinzu kommt, dass sich die Kanalübertragungseigenschaften mit der Zeit stark verändern können („Zeitvarianz”, Beispiel: Mobilfunk).
Zusätzlich sind stets die bei der Signalübertragung auftretenden Störsignale zu berücksichtigen. Hier kann man als Beispiele nennen:
- Rauschsignale – zum Beispiel Widerstands- und Halbleiterrauschen,
- Impulsstörungen – zum Beispiel Starkstromleitungen, Funkenstörungen und Entladungen,
- Nachbarkanalstörungen (Übersprechen anderer Nutzer, Interferenzen, Kreuzmodulation).
Sie finden Grundlegendes über die Modellierung des Nachrichtenkanals allgemein und des einfachen AWGN-Kanals im Lernvideo Eigenschaften des Übertragungskanals.
Empfänger – Nachrichtensinke
Als Beispiele für die Nachrichtensinke können wir nennen:
- Auge und Ohr des Menschen,
- Videorecorder und Anrufaufzeichner,
- ein Smartphone, das eine Datei aus dem Internet herunterlädt, oder
- eine Steuerungsanlage, die empfangene Mess–Signale verarbeitet.
Damit zumindest im – in der Praxis allerdings nie erreichbaren – Idealfall das Sinkensignal $v(t)$ mit dem Quellensignal $q(t)$ übereinstimmen könnte, müssen durch den Empfänger alle sendeseitig getroffenen Maßnahmen rückgängig gemacht werden.
Entsprechende Funktionseinheiten des Empfängers sind:
- Wandler – zum Beispiel ein Lautsprecher zur Umwandlung eines elektrischen in ein akustisches Signal (Gegenstück zum Mikrofon),
- Demodulation – zum Beispiel Frequenzrücksetzung des Signals in den ursprünglichen Frequenzbereich (Gegenstück zum AM/FM/PM-Modulator),
- Signalrücksetzung – zum Beispiel die Rekonstruktion des Analogsignals aus den digitalen Abtastwerten (D/A-Wandler ⇒ Gegenstück zum A/D-Wandler),
- Decodierung – zum Beispiel mit der Möglichkeit zur Fehlererkennung und Fehlerkorrektur (Gegenstück zum Kanalcodierer).
Eine weitere wichtige Aufgabe des Empfängers besteht darin, die bei der Übertragung aufgetretenen Signalverfälschungen und Störungen möglichst gut zu beseitigen.
Die Realisierung solcher Systemkomponenten für Sender und Empfänger geschieht durch verschiedene elektrische Netzwerke und Baugruppen. Auch hier lassen sich beispielhaft einige Funktionseinheiten nennen:
- Verstärker, Filter und Entzerrer,
- Oszillatoren und nichtlineare Komponenten zur (De-)Modulation und Synchronisation,
- digitale Signalverarbeitungskomponenten und Signalprozessoren.
Signalverfälschungen
Es wurde bereits angesprochen, dass im Idealfall $v(t) = q(t)$ sein sollte. Gilt jedoch wie bei jedem realen Übertragungskanal $r(t) \neq s(t)$, so wird sich natürlich auch das Sinkensignal $v(t)$ vom Quellensignal $q(t)$ unterscheiden. Hierzu einige Beispiele:
$\text{Definition:}$ Man spricht von Rauschen, wenn für das Sinkensignal gilt:
- \[ v(t)=q(t)+n(t).\]
Der additive Rauschanteil $n(t)$ ist stets von stochastischer Natur und hat meist keinerlei Bezug zum Nachrichtensignal $q(t)$. Ein solcher Rauschterm ist bei jeder Übertragung unvermeidlich.
$\text{Definition:}$ Die Übertragung ist verzerrungsfrei, wenn das Sinkensignal wie folgt lautet:
- \[v(t)=a \cdot q(t-\tau)+n(t).\]
Das Sinkensignal unterscheidet sich in diesem Falll vom Quellensignal – außer durch den Störanteil $n(t)$ – nur noch durch den (für alle Frequenzen gleichen) Dämpfungsfaktor $\alpha$ und die (ebenfalls für alle Frequenzen gleiche) Laufzeit $\tau$.
$\text{Definition:}$ Ist die Gleichung $v(t)=a\cdot q(t-\tau)+n(t)$ nicht erfüllt, so liegen Verzerrungen vor. Man unterscheidet zwischen
wie im Buch Lineare zeitinvariante Systeme beschrieben wird.
Wir verweisen in diesem Zusammenhang auf das Lernvideo Lineare und nichtlineare Verzerrungen.
Hier nochmals in etwas anderen Worten:
- Der Dämpfungsfaktor $\alpha$ bewirkt nur, dass das Signal $v(t)$ etwas „leiser“ ist als $q(t)$; beide Signale haben aber die gleiche Form.
- Die Laufzeit $\tau$ führt dazu, dass das Signal $v(t)$ am Empfänger später ankommt, als $q(t)$ gesendet wurde.
Beide Effekte sind für eine unidirektionale Übertragung nicht sonderlich störend: Man kann zum Beispiel immer noch von einer Live-Übertragung sprechen, wenn das Fernsehbild um (Bruchteille von) Sekunden verzögert ankommt.
Bei einer bidirektionalen Übertragung kann eine zu lange Laufzeit allerdings zu Problemen führen. Bei einem Telefonat fallen sich dann die beiden Gesprächspartner gegenseitig ins Wort.
$\text{Beispiel 3:}$ Die hier benutzten Begriffe sollen nun an einem Bildsignal verdeutlicht werden.
Rechts sehen Sie als Orginalbild eine Farbschablone mit $291 × 218$ Pixeln und $24$ Bit Farbtiefe. Von den möglichen $2^{24} = 16\hspace{0.08cm} 777\hspace{0.08cm} 216$ Farben sind hier allerdings nur wenige benutzt.
- Im linken unteren Bild ist dem Signal additives Rauschen $n(t)$ überlagert, was sich als „Schnee” bemerkbar macht.
- Das rechte untere Bild zeigt den Einfluss von (nichtlinearen) Verzerrungen, die bei der gewählten Einstellung der CCD-Kamera sowohl zu einer Verfälschung der Helligkeitswerte als auch der Farbinformationen führen.
- Im markierten Feld der Grautreppe stimmt die Helligkeit in etwa mit dem Orginalbild (oben) überein.
- Dagegen erscheinen andere Felder als zu hell oder zu dunkel bzw. mit Fehlfarben belegt.
- Rauscheffekte spielen im rechten Bild keine Rolle im Gegensatz zum linken Bild.
Aufgaben zum Kapitel
Quellenverzeichnis
- ↑ Kaindl, M.: Kanalcodierung für Sprache und Daten in GSM-Systemen. Dissertation. Lehrstuhl für Nachrichtentechnik, TU München. VDI Fortschritt-Berichte, Reihe 10, Nr. 764, 2005.