Application to Digital Signal Transmission

1. Information Theory
2. Information zwischen zwei wertdiskreten Zufallsgrößen
3. Application to Digital Signal Transmission

• Previous page
• Next page

• Previous page
• Next page

Information-theoretical model of digital signal transmission

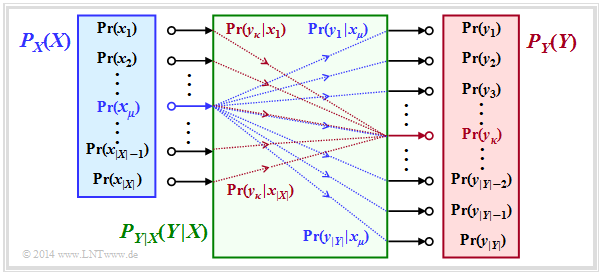
The entropies defined so far in general terms are now applied to digital signal transmission, whereby we assume a discrete memoryless channel  (DMC)  according to the graphic:

Digital signal transmission model under consideration

• The set of possible source symbols is characterised by the discrete random variable  $X$ , where  $|X|$  indicates the source symbol range:

$$X = \{\hspace{0.05cm}x_1\hspace{0.05cm}, \hspace{0.15cm} x_2\hspace{0.05cm},\hspace{0.15cm} \text{...}\hspace{0.1cm} ,\hspace{0.15cm} x_{\mu}\hspace{0.05cm}, \hspace{0.15cm}\text{...}\hspace{0.1cm} , \hspace{0.15cm} x_{|X|}\hspace{0.05cm}\}\hspace{0.05cm}.$$

• Correspondingly,  $Y$  characterises the set of sink symbols with the symbol range  $|Y|$:

$$Y = \{\hspace{0.05cm}y_1\hspace{0.05cm}, \hspace{0.15cm} y_2\hspace{0.05cm},\hspace{0.15cm} \text{...}\hspace{0.1cm} ,\hspace{0.15cm} y_{\kappa}\hspace{0.05cm}, \hspace{0.15cm}\text{...}\hspace{0.1cm} , \hspace{0.15cm} Y_{|Y|}\hspace{0.05cm}\}\hspace{0.05cm}.$$

• Usually  $|Y| = |X|$is valid.  Also possible is  $|Y| > |X|$, for example with the  Binary Erasure Channel  (BEC) with  $X = \{0,\ 1\}$,  $Y = \{0,\ 1,\ \ \text{E}\}$   ⇒   $|X| = 2$,  $|Y| = 3$.
• The sink symbol  $\rm E$  indicates an erasure.  The event  $Y=\text{E}$  indicates that a decision for  $0$  or for  $1$  would be too uncertain.
• The symbol probabilities of the source and sink are accounted for in the graph by the probability functions  $P_X(X)$  and  $P_Y(Y)$ , where:

$$P_X(x_{\mu}) = {\rm Pr}( X = x_{\mu})\hspace{0.05cm}, \hspace{0.3cm} P_Y(y_{\kappa}) = {\rm Pr}( Y = y_{\kappa})\hspace{0.05cm}.$$

• Let it hold:   $P_X(X)$  and  $P_Y(Y)$  contain no zeros   ⇒   $\text{supp}(P_X) = P_X$  and  $\text{supp}(P_Y) = P_Y$.
  This precondition facilitates the model description without loss of generality.
• All transition probabilities of the discrete memoryless channel   $\rm (DMC)$  are captured by the  conditional probability function  $P_{Y|X}(Y|X)$ .
  Mit  $x_μ ∈ X$  and  $y_κ ∈ Y$ , the following definition applies to this:

$$P_{Y\hspace{0.01cm}|\hspace{0.01cm}X}(y_{\kappa}\hspace{0.01cm} |\hspace{0.01cm} x_{\mu}) = {\rm Pr}(Y\hspace{-0.1cm} = y_{\kappa}\hspace{0.03cm} | \hspace{0.03cm}X \hspace{-0.1cm}= x_{\mu})\hspace{0.05cm}.$$

The green block in the graph marks  $P_{Y|X}(⋅)$  with  $|X|$  inputs and  $|Y|$  outputs.  Blue connections mark transition probabilities  $\text{Pr}(y_i | x_μ)$  starting from  $x_μ$  with  $1 ≤ i ≤ |Y|$, while all red connections end at  $y_κ$:    $\text{Pr}(y_κ | x_i)$  with  $1 ≤ i ≤ |X|$.

Before we give the entropies for the individual probability functions, viz.

$$P_X(X) ⇒ H(X),\hspace{0.5cm} P_Y(Y) ⇒ H(Y), \hspace{0.5cm} P_{XY}(X) ⇒ H(XY), \hspace{0.5cm} P_{Y|X}(Y|X) ⇒ H(Y|X),\hspace{0.5cm} P_{X|Y}(X|Y) ⇒ H(X|Y),$$

the above statements are to be illustrated by an example.

Digital Channel Model Binary Erasure Channel

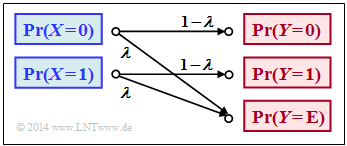
$\text{Example 1}$:  In the book „Channel Coding” we also deal with the  Binary Erasure Channel  $\rm (BEC)$, which is sketched in a somewhat modified form on the right.   The following prerequisites apply:

• Let the input alphabet be binary  ⇒   $X = \{0,\ 1 \}$   ⇒   $\vert X\vert = 2$while three values are possible at the output   ⇒   $Y = \{0,\ 1,\ \text{E} \}$   ⇒   $\vert Y\vert = 3$.
• The symbol  $\text{E}$  indicates the case that the receiver cannot decide for one of the binary symbols  $0$  or  $1$  due to too much channel interference.  „E” stands for erasure.
• With the  $\rm BEC$  according to the above sketch, both a transmitted  $0$  and a  $1$  are erased with probability  $λ$  while the probability of a correct transmission is  $1 – λ$  in each case.
• In contrast, transmission errors are excluded by the BEC model  
  ⇒   the conditional probabilities  $\text{Pr}(Y = 1 \vert X = 0)$  and  $\text{Pr}(Y = 0 \vert X = 1)$  are both zero.

At the transmitter, the zeros and ones would not necessarily be equally probable.  Rather, we use the probability functions

$$\begin{align*}P_X(X) & = \big ( {\rm Pr}( X = 0)\hspace{0.05cm},\hspace{0.2cm} {\rm Pr}( X = 1) \big )\hspace{0.05cm},\\ P_Y(Y) & = \big ( {\rm Pr}( Y = 0)\hspace{0.05cm},\hspace{0.2cm} {\rm Pr}( Y = 1)\hspace{0.05cm},\hspace{0.2cm} {\rm Pr}( Y = {\rm E}) \big )\hspace{0.05cm}.\end{align*}$$

From the above model we then get:

$$\begin{align*}P_Y(0) & = {\rm Pr}( Y \hspace{-0.1cm} = 0) = P_X(0) \cdot ( 1 - \lambda)\hspace{0.05cm}, \\ P_Y(1) & = {\rm Pr}( Y \hspace{-0.1cm} = 1) = P_X(1) \cdot ( 1 - \lambda)\hspace{0.05cm}, \\ P_Y({\rm E}) & = {\rm Pr}( Y \hspace{-0.1cm} = {\rm E}) = P_X(0) \cdot \lambda \hspace{0.1cm}+\hspace{0.1cm} P_X(1) \cdot \lambda \hspace{0.05cm}.\end{align*}$$

If we now take  $P_X(X)$  and  $P_Y(Y)$  to be vectors, the result can be represented as follows:

$$P_{\hspace{0.05cm}Y}(Y) = P_X(X) \cdot P_{\hspace{0.05cm}Y\hspace{-0.01cm}\vert \hspace{-0.01cm}X}(Y\hspace{-0.01cm} \vert \hspace{-0.01cm} X) \hspace{0.05cm},$$

where the transition probabilities  $\text{Pr}(y_κ\vert x_μ)$  are accounted for by the following matrix:

$$P_{\hspace{0.05cm}Y\hspace{-0.01cm} \vert \hspace{-0.01cm}X}(Y\hspace{-0.01cm} \vert \hspace{-0.01cm} X) = \begin{pmatrix} 1 - \lambda & 0 & \lambda\\ 0 & 1 - \lambda & \lambda \end{pmatrix}\hspace{0.05cm}.$$

Note:

• We have chosen this representation only to simplify the description.
• $P_X(X)$  and  $P_Y(Y)$  are not vectors in the true sense and  $P_{Y \vert X}(Y\vert X)$  is not a matrix either.

Directional diagram for digital signal transmission

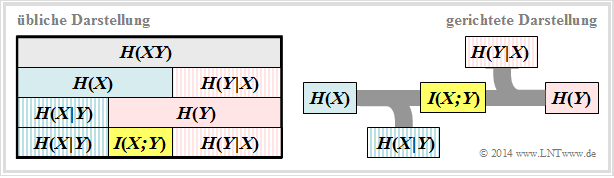
All entropies defined in the  last chapter  also apply to digital signal transmission.  However, it is expedient to choose the right-hand diagram instead of the diagram used so far, corresponding to the left-hand diagram, in which the direction from source  $X$  to sink  $Y$  is recognisable.

Two Information-Theoretical Models for Digital Signal Transmission

Let us now interpret the right graph starting from the general   DMC channel model  :

• The  source entropy  $H(X)$  denotes the average information content of the source symbol sequence.   With the symbol range  $|X|$  applies:

$$H(X) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_X(X)}\right ] \hspace{0.1cm} = -{\rm E} \big [ {\rm log}_2 \hspace{0.1cm}{P_X(X)}\big ] \hspace{0.2cm} =\hspace{0.2cm} \sum_{\mu = 1}^{|X|} P_X(x_{\mu}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_X(x_{\mu})} \hspace{0.05cm}.$$

• The  equivocation  $H(X|Y)$  indicates the average information content that an observer who knows exactly about sink  $Y$  gains by observing source  $X$ :

$$H(X|Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}X\hspace{-0.01cm}|\hspace{-0.01cm}Y}(X\hspace{-0.01cm} |\hspace{0.03cm} Y)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|} P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}X\hspace{-0.01cm}|\hspace{0.03cm}Y} (\hspace{0.05cm}x_{\mu}\hspace{0.03cm} |\hspace{0.05cm} y_{\kappa})} \hspace{0.05cm}.$$

• The equivocation is the portion of the source entropy  $H(X)$ that is lost due to channel interference  (for digital channel: transmission errors)  .  The mutual information $I(X; Y)$ remains, which reaches the sink:

$$I(X;Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(X, Y)}{P_X(X) \cdot P_Y(Y)}\right ] \hspace{0.2cm} = H(X) - H(X|Y) \hspace{0.05cm}.$$

• The  irrelevance  $H(Y|X)$  indicates the average information content that an observer who knows exactly about the source  $X$  gains by observing the sink  $Y$ :

$$H(Y|X) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{-0.01cm}X}(Y\hspace{-0.01cm} |\hspace{0.03cm} X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|} P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.03cm}X} (\hspace{0.05cm}y_{\kappa}\hspace{0.03cm} |\hspace{0.05cm} x_{\mu})} \hspace{0.05cm}.$$

• The  sink entropy  $H(Y)$, the mean information content of the sink, is the sum of the useful mutual information  $I(X; Y)$  and the irrelevance  $H(Y|X)$, which comes exclusively from channel errors:

$$H(Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_Y(Y)}\right ] \hspace{0.1cm} = -{\rm E} \big [ {\rm log}_2 \hspace{0.1cm}{P_Y(Y)}\big ] \hspace{0.2cm} =I(X;Y) + H(Y|X) \hspace{0.05cm}.$$

Calculation of the mutual information for the binary channel

These definitions will now be illustrated by an example.   We deliberately avoid simplifying the calculations by exploiting symmetries.

General model of the binary channel

$\text{Example 2}$:  We consider the general binary channel without memory according to the sketch.  Let the falsification probabilities be:

$$\begin{align*}\varepsilon_0 & = {\rm Pr}(Y\hspace{-0.1cm} = 1\hspace{0.05cm}\vert X \hspace{-0.1cm}= 0) = 0.01\hspace{0.05cm},\\ \varepsilon_1 & = {\rm Pr}(Y\hspace{-0.1cm} = 0\hspace{0.05cm} \vert X \hspace{-0.1cm}= 1) = 0.2\hspace{0.05cm}\end{align*}$$

$$\Rightarrow \hspace{0.3cm} P_{\hspace{0.05cm}Y\hspace{-0.01cm} \vert \hspace{-0.01cm}X}(Y\hspace{-0.01cm} \vert \hspace{-0.01cm} X) = \begin{pmatrix} 1 - \varepsilon_0 & \varepsilon_0\\ \varepsilon_1 & 1 - \varepsilon_1 \end{pmatrix} = \begin{pmatrix} 0.99 & 0.01\\ 0.2 & 0.8 \end{pmatrix} \hspace{0.05cm}.$$

Furthermore, we assume source symbols that are not equally probable:

$$P_X(X) = \big ( p_0, p_1 \big )= \big ( 0.1,\ 0.9 \big ) \hspace{0.05cm}.$$

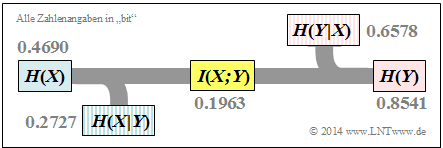
With the  binary entropy function  $H_{\rm bin}(p)$ , we thus obtain for the source entropy:

$$H(X) = H_{\rm bin} (0.1) = 0.4690 \,{\rm bit} \hspace{0.05cm}.$$

For the probability function of the sink as well as for the sink entropy we thus obtain:

$$P_Y(Y) = \big [ {\rm Pr}( Y\hspace{-0.1cm} = 0)\hspace{0.05cm}, \ {\rm Pr}( Y \hspace{-0.1cm}= 1) \big ] = \big ( p_0\hspace{0.05cm},\ p_1 \big ) \cdot \begin{pmatrix} 1 - \varepsilon_0 & \varepsilon_0\\ \varepsilon_1 & 1 - \varepsilon_1 \end{pmatrix} $$

$$\begin{align*}\Rightarrow \hspace{0.3cm} {\rm Pr}( Y \hspace{-0.1cm}= 0)& = p_0 \cdot (1 - \varepsilon_0) + p_1 \cdot \varepsilon_1 = 0.1 \cdot 0.99 + 0.9 \cdot 0.2 = 0.279\hspace{0.05cm},\\ {\rm Pr}( Y \hspace{-0.1cm}= 1) & = 1 - {\rm Pr}( Y \hspace{-0.1cm}= 0) = 0.721\end{align*}$$

$$\Rightarrow \hspace{0.2cm} H(Y) = H_{\rm bin} (0.279) = 0.8541 \,{\rm bit} \hspace{0.05cm}. $$

The joint probabilities  $p_{\mu \kappa} = \text{Pr}\big[(X = μ) ∩ (Y = κ)\big]$  between source and sink are:

$$\begin{align*}p_{00} & = p_0 \cdot (1 - \varepsilon_0) = 0.099\hspace{0.05cm},\hspace{0.5cm}p_{01}= p_0 \cdot \varepsilon_0 = 0.001\hspace{0.05cm},\\ p_{10} & = p_1 \cdot (1 - \varepsilon_1) = 0.180\hspace{0.05cm},\hspace{0.5cm}p_{11}= p_1 \cdot \varepsilon_1 = 0.720\hspace{0.05cm}.\end{align*}$$

From this one obtains for

• the  joint entropy:

$$H(XY) = p_{00}\hspace{-0.05cm} \cdot \hspace{-0.05cm}{\rm log}_2 \hspace{0.05cm} \frac{1}{p_{00} \rm } + p_{01} \hspace{-0.05cm} \cdot \hspace{-0.05cm}{\rm log}_2 \hspace{0.05cm} \frac{1}{p_{01} \rm } + p_{10}\hspace{-0.05cm} \cdot \hspace{-0.05cm} {\rm log}_2 \hspace{0.05cm} \frac{1}{p_{10} \rm } + p_{11} \hspace{-0.05cm} \cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.05cm} \frac{1}{p_{11}\rm } = 1.1268\,{\rm bit} \hspace{0.05cm},$$

• the  mutual information:

$$I(X;Y) = H(X) + H(Y) - H(XY) = 0.4690 + 0.8541 - 1.1268 = 0.1963\,{\rm bit} \hspace{0.05cm},$$

Informationstheoretisches Modell des betrachteten Binärkanals

• the  equivocation:

$$H(X \vert Y) \hspace{-0.01cm} =\hspace{-0.01cm} H(X) \hspace{-0.01cm} -\hspace{-0.01cm} I(X;Y) \hspace{-0.01cm} $$

$$\Rightarrow \hspace{0.3cm} H(X \vert Y) \hspace{-0.01cm} = \hspace{-0.01cm} 0.4690\hspace{-0.01cm} -\hspace{-0.01cm} 0.1963\hspace{-0.01cm} =\hspace{-0.01cm} 0.2727\,{\rm bit} \hspace{0.05cm},$$

• the irrelevance:

$$H(Y \vert X) = H(Y) - I(X;Y) $$

$$\Rightarrow \hspace{0.3cm} H(Y \vert X) = 0.8541 - 0.1963 = 0.6578\,{\rm bit} \hspace{0.05cm}.$$

The results are summarised in the graph.

Notes:

• The equivocation and irrelevance could also have been calculated directly (but with extra effort) from the corresponding probability functions.
• For example, the irrelevance:

$$H(Y|X) = \hspace{-0.2cm} \sum_{(x, y) \hspace{0.05cm}\in \hspace{0.05cm}XY} \hspace{-0.2cm} P_{XY}(x,\hspace{0.05cm}y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.03cm}X} (\hspace{0.05cm}y\hspace{0.03cm} |\hspace{0.05cm} x)}= p_{00} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1\hspace{-0.08cm} - \hspace{-0.08cm}\varepsilon_0} + p_{01} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon_0} + p_{10} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1\hspace{-0.08cm} - \hspace{-0.08cm}\varepsilon_1} + p_{11} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon_1} = 0.6578\,{\rm bit} \hspace{0.05cm}.$$

Definition and meaning of channel capacity

We further consider a discrete memoryless channel  (DMC)  with a finite number of source symbols   ⇒   $|X|$  and also only finitely many sink symbols   ⇒   $|Y|$, , as shown in the first section of this chapter.

• If one calculates the mutual information  $I(X, Y)$  as last explained in  $\text{example 2}$  ausgeführt,  it also depends on the source statistic   ⇒   $P_X(X)$  .
• Ergo:   The mutual information  $I(X, Y)$  is not a pure channel characteristic.

$\text{Definition:}$  The   channel capacity introduced by  Claude E. Shannon  according to his standard work  [Sha48] reads:

$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$

Since according to this definition the best possible source statistics are always the basis,    $C$  depends only on the channel properties   ⇒   $P_{Y \vert X}(Y \vert X)$ ab, , but not on the source statistics   ⇒   $P_X(X)$.  Often the additional unit „bit/channel use” .

Shannon needed the channel description quantity  $C$  to formulate the channel coding theorem – one of the highlights of the information theory he founded.

$\text{Shannon's channel coding theorem: }$ 

• For every transmission channel with channel capacity  $C > 0$ , there exists (at least) one  $(k, n)$–block code,  whose (block) error probability approaches zero  as long as the code rate  $R = k/n$  is less than or equal to the channel capacity:  

$$R ≤ C.$$

• The prerequisite for this, however,  is that the following applies to the block length of this code:  

$$n → ∞.$$

The proof of this theorem,  which is beyond the scope of our learning tutorial,  can be found for example in  [CT06],  [Kra13]  und  [Meck09].

As will be shown in  task 3.13 ,   the reverse also is true.  This proof can also be found in the literature references just mentioned.

$\text{Reverse of Shannon's channel coding theorem: }$ 

If the rate  $R$  of the  $(n$, $k)$–block code used is greater than the channel capacity  $C$,  then an arbitrarily small block error probability is not achievable.

In the chapter  AWGN model for discrete-time band-limited signals  it is explained in connection with the continuous-value  AWGN channel model    what phenomenally great significance Shannon's information-theoretical theorem has for the entire field of information technology,  not only for those interested exclusively in theory,  but also for practitioners.

Channel capacity of a binary channel

General model of the binary channel

Die Transinformation des allgemeinen (unsymmetrischen) Binärkanals gemäß dieser Skizze wurde im  $\text{Beispiel 2}$  berechnet.  Bei diesem Modell werden die Eingangssymbole  $0$  und  $1$  unterschiedlich stark verfälscht:

$$P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{-0.01cm}X}(Y\hspace{-0.01cm} |\hspace{-0.01cm} X) = \begin{pmatrix} 1 - \varepsilon_0 & \varepsilon_0\\ \varepsilon_1 & 1 - \varepsilon_1 \end{pmatrix} \hspace{0.05cm}.$$

Die Transinformation lässt sich mit der Wahrscheinlichkeitsfunktion  $P_X(X) = (p_0,\ p_1)$  wie folgt darstellen:

$$I(X ;Y) = \sum_{\mu = 1}^{2} \hspace{0.1cm}\sum_{\kappa = 1}^{2} \hspace{0.2cm} {\rm Pr} (\hspace{0.05cm}y_{\kappa}\hspace{0.03cm} |\hspace{0.05cm} x_{\mu}) \cdot {\rm Pr} (\hspace{0.05cm}x_{\mu}\hspace{0.05cm})\cdot {\rm log}_2 \hspace{0.1cm} \frac{{\rm Pr} (\hspace{0.05cm}y_{\kappa}\hspace{0.03cm} |\hspace{0.05cm} x_{\mu})}{{\rm Pr} (\hspace{0.05cm}y_{\kappa})} $$

$$\begin{align*}\Rightarrow \hspace{0.3cm} I(X ;Y) &= \hspace{-0.01cm} (1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_0) \cdot p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_0}{(1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_0) \cdot p_0 + \varepsilon_1 \cdot p_1} + \varepsilon_0 \cdot p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{\varepsilon_0}{(1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_0) \cdot p_0 + \varepsilon_1 \cdot p_1} + \\ & + \hspace{-0.01cm} \varepsilon_1 \cdot p_1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{\varepsilon_1}{\varepsilon_0 \cdot p_0 + (1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_1) \cdot p_1} + (1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_1) \cdot p_1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_1}{\varepsilon_0 \cdot p_0 + (1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_1) \cdot p_1} \hspace{0.05cm}.\end{align*}$$

Transinformation für den
„unsymmetrischen Binärkanal”

$\text{Beispiel 3}$:  Im Folgenden setzen wir  $ε_0 = 0.01$  und  $ε_1 = 0.2$.

In der Spalte 4 nebenstehender Tabelle ist (grün hinterlegt) die Transinformation  $I(X; Y)$  dieses unsymmetrischen Binärkanals abhängig von der Quellensymbolwahrscheinlichkeit  $p_0 = {\rm Pr}(X = 0)$  angegeben.  Man erkennt:

• Die Transinformation hängt von den Symbolwahrscheinlichkeiten $p_0$ und $p_1 = 1 - p_0$ ab.
• Der Maximalwert von  $I(X; Y)$  ergibt sich hier zu  $p_0 ≈ 0.55$    ⇒    $p_1 ≈ 0.45$.
• Das Ergebnis  $p_0 > p_1$  folgt aus der Relation  $ε_0 < ε_1$  (die Null wird weniger verfälscht).
• Die Kapazität dieses Kanals ist  $C = 0.5779 \ \rm bit/Kanalzugriff$.

In obiger Gleichung ist als Sonderfall auch der  Binary Symmetric Channel  $\rm (BSC)$  mit den Parametern  $ε = ε_0 = ε_1$  mitenthalten.  Hinweise:

• In  Aufgabe 3.10  wird die Transinformation des BSC–Kanals für die Systemparameter  $ε = 0.1$  und  $p_0 = 0.2$  berechnet.
• In der  Aufgabe 3.10Z  wird dessen Kanalkapazität wie folgt angegeben:

$$C_{\rm BSC} = 1 - H_{\rm bin} (\varepsilon) \hspace{0.05cm}.$$

Eigenschaften symmetrischer Kanäle

Die Kapazitätsberechnung des (allgemeinen)  diskreten gedächtnislosen Kanals  ist oftmals aufwändig.  Sie vereinfacht sich entscheidend, wenn Symmetrien des Kanals ausgenutzt werden. 

Die Grafik zeigt zwei Beispiele:

• Beim  gleichmäßig dispersiven Kanal  (englisch: Uniformly Dispersive Channel )  ergibt sich für alle Quellensymbole  $x ∈ X$  die genau gleiche Menge an Übergangswahrscheinlichkeiten   ⇒   $\{P_{Y\hspace{0.03cm}|\hspace{0.01cm}X}(y_κ\hspace{0.05cm}|\hspace{0.05cm}x)\}$  mit  $1 ≤ κ ≤ |Y|$.  Für die Werte  $q$,  $r$,  $s$  muss hier stets  $q + r + s = 1$  gelten (linke Grafik).
• Beim  gleichmäßig fokussierenden Kanal  (englisch:  Uniformely Focusing Channel )  ergibt sich für alle Sinkensymbole  $y ∈ Y$  die gleiche Menge an Übergangswahrscheinlichkeiten   ⇒   $\{P_{Y\hspace{0.03cm}|\hspace{0.01cm}X}(y\hspace{0.05cm}|\hspace{0.05cm}x_μ)\}$  mit  $1 ≤ μ ≤ |X|$.  Hier muss nicht notwendigerweise  $t + u + v = 1$  gelten (rechte Grafik).

Beispiele symmetrischer Kanäle

$\text{Definition:}$  Ist ein diskreter gedächtnisloser Kanal sowohl gleichmäßig dispersiv als auch gleichmäßig fokussierend,  so liegt ein  streng symmetrischer Kanal  (englisch:  Strongly Symmetric Channel )  vor.  Bei gleichverteiltem Quellenalphabet besitzt dieser die Kapazität

$$C = {\rm log}_2 \hspace{0.1cm} \vert Y \vert + \sum_{y \hspace{0.05cm}\in\hspace{0.05cm} Y} \hspace{0.1cm} P_{\hspace{0.03cm}Y \vert \hspace{0.01cm} X}(y\hspace{0.05cm} \vert \hspace{0.05cm}x) \cdot {\rm log}_2 \hspace{0.1cm}P_{\hspace{0.01cm}Y \vert \hspace{0.01cm} X}(y\hspace{0.05cm}\vert\hspace{0.05cm} x) \hspace{0.05cm}.$$

Für diese Gleichung kann jedes beliebige  $x ∈ X$  herangezogen werden.

Diese Definition soll nun durch ein Beispiel verdeutlicht werden.

Streng symmetrischer Kanal mit  $\vert X \vert = \vert Y \vert= 3$

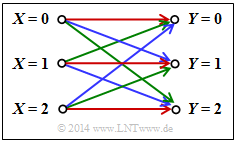
$\text{Beispiel 4}$:  Beim betrachteten Kanal gibt es Verbindungen zwischen allen  $ \vert X \vert = 3$  Eingängen und allen  $ \vert Y \vert = 3$  Ausgängen:

• Eine rote Verbindung steht für  $P_{Y \hspace{0.03cm}\vert\hspace{0.01cm} X}(y_κ \hspace{0.05cm} \vert \hspace{0.05cm} x_μ) = 0.7$.
• Eine blaue Verbindung steht für  $P_{Y \hspace{0.03cm}\vert\hspace{0.01cm} X}(y_κ \hspace{0.05cm}\vert \hspace{0.05cm} x_μ) = 0.2$.
• Eine grüne Verbindung steht für  $P_{Y \hspace{0.03cm}\vert\hspace{0.01cm} X}(y_κ \hspace{0.05cm}\vert\hspace{0.05cm} x_μ) = 0.1$.

Nach obiger Gleichung gilt dann für die Kanalkapazität:

$$C = {\rm log}_2 \hspace{0.1cm} (3) + 0.7 \cdot {\rm log}_2 \hspace{0.1cm} (0.7) + 0.2 \cdot {\rm log}_2 \hspace{0.1cm} (0.2) + 0.1 \cdot {\rm log}_2 \hspace{0.1cm} (0.1) = 0.4282 \,\,{\rm bit} \hspace{0.05cm}.$$

Hinweise:

• Der Zusatz „die gleiche Menge an Übergangswahrscheinlichkeiten” bedeutet nicht, dass $P_{Y \hspace{0.03cm}\vert\hspace{0.01cm} X}(y_κ \hspace{0.05cm}\vert\hspace{0.05cm} x_1) = P_{Y \hspace{0.03cm}\vert\hspace{0.01cm} X}(y_κ \hspace{0.05cm}\vert\hspace{0.05cm} x_2) = P_{Y \hspace{0.03cm}\vert\hspace{0.01cm} X}(y_κ \hspace{0.05cm}\vert\hspace{0.05cm} x_3)$ gelten muss.
• Vielmehr geht hier von jedem Eingang ein roter, ein blauer und ein grüner Pfeil ab und an jedem Ausgang kommt ein roter, ein blauer und ein grüner Pfeil an.
• Die jeweiligen Reihenfolgen permutieren:   R – G – B,     B – R – G,     G – B – R.

Ein Beispiel für einen streng symmetrischen Kanal ist der  Binary Symmetric Channel  $\rm (BSC)$.  Dagegen ist der  Binary Erasure Channel  $\rm (BEC)$  nicht streng symmetrisch,

• da er zwar gleichmäßig dispersiv ist,
• aber nicht gleichmäßig fokussierend.

Die nachfolgende Definition ist weniger restriktiv als die vorherige des streng symmetrischen Kanals.

$\text{Definition:}$  Ein  symmetrischer Kanal  (englisch:  Symmetric Channel )  liegt vor,

• wenn er in mehrere  $($allgemein $L)$  streng symmetrische Teilkanäle aufgeteilt werden kann,
• indem das Ausgangsalphabet  $Y$  in  $L$  Teilmengen  $Y_1$, ... , $Y_L$  aufgespalten wird.

Ein solcher symmetrischer Kanal besitzt die folgende Kapazität:

$$C = \sum_{l \hspace{0.05cm}=\hspace{0.05cm} 1}^{L} \hspace{0.1cm} p_{\hspace{0.03cm}l} \cdot C_{\hspace{0.03cm}l} \hspace{0.05cm}.$$

Hierbei sind folgende Bezeichnungen verwendet:

• $p_{\hspace{0.03cm}l}$  gibt die Wahrscheinlichkeit an,  dass der  $l$–te Teilkanal ausgewählt wird,
• $C_{\hspace{0.03cm}l}$  ist die Kanalkapazität dieses  $l$–ten Teilkanals.

Symmetrischer Kanal, bestehend aus zwei
streng symmetrischen Teilkanälen  $\rm A$  und  $\rm B$

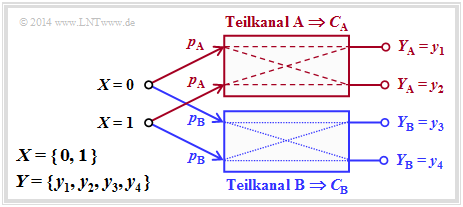
Die Grafik verdeutlicht diese Definition für  $L = 2$, wobei die Teilkanäle mit  $\rm A$  und  $\rm B$  bezeichnet sind.

• An den unterschiedlich gezeichneten Übergängen (gestrichelt oder gepunktet) erkennt man, dass die zwei Teilkanäle verschieden sein können,  so dass allgemein  $C_{\rm A} ≠ C_{\rm B}$  gelten wird.
• Für die Kapazität des Gesamtkanals erhält man somit allgemein:

$$C = p_{\rm A} \cdot C_{\rm A} + p_{\rm B} \cdot C_{\rm B} \hspace{0.05cm}.$$

• Über die Struktur der beiden Teilkanäle wird hier keine Aussage gemacht.

Im folgenden Beispiel wird sich zeigen, dass auch der  Binary Erasure Channel  $\rm (BEC)$  durch diese Grafik grundsätzlich beschreibbar ist.  Allerdings müssen dann die zwei Ausgangssysmbole  $y_3$  und  $y_4$  zu einem einzigen Symbol zusammengefasst werden.

$\rm (BEC)$  in zwei verschiedenen Darstellungen

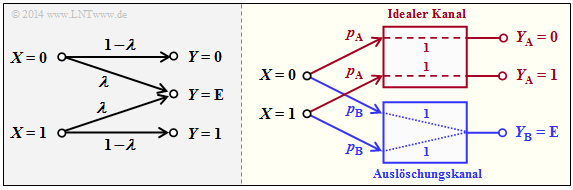
$\text{Beispiel 5}$:  Die linke Grafik zeigt die übliche Darstellung des  Binary Erasure Channels  $\rm (BEC)$  mit Eingang  $X = \{0,\ 1\}$  und Ausgang  $Y = \{0,\ 1,\ \text{E} \}$.

Teilt man diesen entsprechend der rechten Grafik auf in

• einen idealen Kanal  $(y = x)$  für

$$y ∈ Y_{\rm A} = \{0, 1\} \ \ ⇒ \ \ C_{\rm A} = 1 \ \rm bit/use,$$

• einen Auslöschungskanal für

$$y ∈ Y_{\rm B} = \{\rm E \} \ \ ⇒ \ \ C_{\rm B} = 0,$$

so ergibt sich mit den Teilkanalgewichtungen  $p_{\rm A} = 1 – λ$  und  $p_{\rm B} = λ$  für die Kanalkapazität:

$$C_{\rm BEC} = p_{\rm A} \cdot C_{\rm A} = 1 - \lambda \hspace{0.05cm}.$$

Beide Kanäle sind streng symmetrisch.  Für den (idealen) Kanal  $\rm A$  gilt gleichermaßen

• für  $X = 0$  und  $X = 1$:     $\text{Pr}(Y = 0 \hspace{0.05cm}\vert \hspace{0.05cm} X) = \text{Pr}(Y = 1 \hspace{0.05cm} \vert\hspace{0.05cm} X) = 1 - λ$   ⇒   gleichmäßig dispersiv,
• für  $Y = 0$  und   $Y = 1$:     $\text{Pr}(Y \hspace{0.05cm} \vert \hspace{0.05cm} X= 0) = Pr(Y \hspace{0.05cm}\vert\hspace{0.05cm} X = 1) = 1 - λ$   ⇒   gleichmäßig fokussierend.

Entsprechendes gilt für den Auslöschungskanal  $\rm B$.

In der  Aufgabe 3.12  wird sich zeigen, dass die Kapazität des Kanalmodells  Binary Symmetric Error & Erasure Channel  $\rm (BSEC)$  in gleicher Weise berechnet werden kann.  Man erhält:

$$C_{\rm BSEC} = (1- \lambda) \cdot \left [ 1 - H_{\rm bin}(\frac{\varepsilon}{1- \lambda}) \right ]$$

• mit der Verfälschungswahrscheinlichkeit  $ε$
• und der Auslöschungswahrscheinlichkeit  $λ$.

Einige Grundlagen der Kanalcodierung

Um das Kanalcodierungstheorem richtig interpretieren zu können, sind einige Grundlagen der  Kanalcodierung  (englisch:  Channel Coding)  erforderlich.  Dieses äußerst wichtige Gebiet der Nachrichtentechnik wird in unserem Lerntutorial  $\rm LNTwww$  in einem eigenen Buch namens  Channel Coding  behandelt.

Modell für die binär–codierte Informationsübertragung

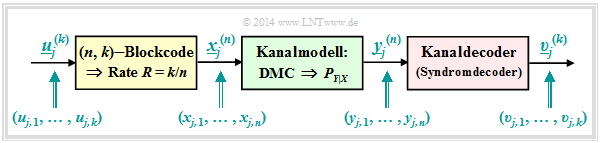
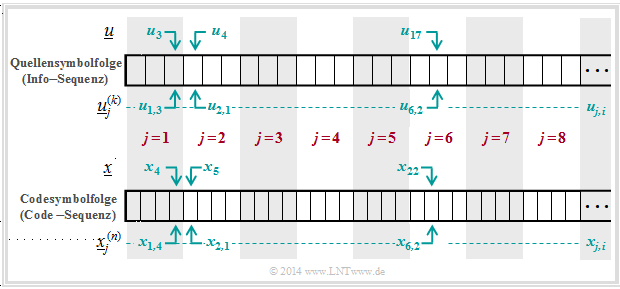
Die folgende Beschreibung bezieht sich auf das stark vereinfachte Modell für  binäre Blockcodes:

• Die unendlich lange Quellensymbolfolge  $\underline{u}$  (hier nicht dargestellt)  wird in Blöcke zu jeweils  $k$ Bit unterteilt.  Wir bezeichnen den Informationsblock mit der laufenden Nummerierung  $j$  mit  $\underline{u}_j^{(k)}$.
• Jeder Informationsblock  $\underline{u}_j^{(k)}$  wird durch den gelb hinterlegten Kanalcoder in ein Codewort  $\underline{x}_j^{(n)}$  umgesetzt, wobei  $n > k$  gelten soll.  Das Verhältnis  $R = k/n$  bezeichnet man als die  Coderate.
• Der  Discrete Memoryless Channel  $\rm (DMC)$  wird durch Übergangswahrscheinlichkeiten  $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(⋅)$  berücksichtigt.  Dieser grün hinterlegte Block bewirkt Fehler auf Bitebene. Es kann also gelten:   $y_{j, \hspace{0.03cm}i} ≠ x_{j,\hspace{0.03cm} i}$.
• Damit können sich auch die aus  $n$  Bit bestehenden Empfangsblöcke  $\underline{y}_j^{(n)}$  von den Codeworten  $\underline{x}_j^{(n)}$ unterscheiden .  Ebenso gilt im allgemeinen für die Blöcke nach dem Deoder:  $\underline{v}_j^{(k)} ≠ \underline{u}_j^{(k)}$.

$\text{Beispiel 6}$:  Die Grafik soll die hier verwendete Nomenklatur am Beispiel  $k = 3$  und  $n = 4$  verdeutlichen.  Dargestellt sind die jeweils ersten acht Blöcke der Informationssequenz  $\underline{u}$  und der  Codesequenz $\underline{x}$.

Zur Bitbezeichnung von Informationsblock und Codewort

Man erkennt folgende Zuordnung zwischen der geblockten und der ungeblockten Beschreibung:

• Bit 3 des 1. Info–Blocks   ⇒   $u_{1,\hspace{0.08cm} 3}$  entspricht dem Symbol  $u_3$  in ungeblockter Darstellung.
• Bit 1 des 2. Info–Blocks   ⇒   $u_{2, \hspace{0.08cm}1}$  entspricht dem Symbol  $u_4$  in ungeblockter Darstellung.
• Bit 2 des 6. Info–Blocks   ⇒   $u_{6, \hspace{0.08cm}2}$  entspricht dem Symbol  $u_{17}$  in ungeblockter Darstellung.
• Bit 4 des 1. Codewortes   ⇒   $x_{1, \hspace{0.08cm}4}$  entspricht dem Symbol  $x_4$  in ungeblockter Darstellung.
• Bit 1 des 2. Codewortes   ⇒   $x_{2, \hspace{0.08cm}1}$  entspricht dem Symbol  $x_5$  in ungeblockter Darstellung.
• Bit 2 des 6. Codewortes   ⇒   $x_{6, \hspace{0.08cm}2}$  entspricht dem Symbol  $x_{22}$  in ungeblockter Darstellung.

Zusammenhang zwischen Blockfehlern und Bitfehlern

Zur Interpretation des Kanalcodierungstheorems benötigen wir noch verschiedene Definitionen für „Fehlerwahrscheinlichkeiten”.  Aus dem obigen Systemmodell lassen sich verschiedene Beschreibungsgrößen ableiten:

$\text{Definitionen:}$

• Die  $\rm {Kanalfehlerwahrscheinlichkeit}$  ergibt sich beim vorliegenden Kanalmodell zu

$${\rm Pr(Kanalfehler)} = {\rm Pr} \left ({y}_{j,\hspace{0.05cm} i} \ne {x}_{j,\hspace{0.05cm} i} \right )\hspace{0.05cm}.$$

Beispielsweise ist beim BSC–Modell  $\text{Pr(Kanalfehler)} = ε$  für alle  $j = 1, 2$, ...  und  $1 ≤ i ≤ n$.

• Die  $\rm {Blockfehlerwahrscheinlichkeit}$  bezieht sich auf die zugeordneten Informationsblöcke am Codereingang   ⇒   $\underline{u}_j^{(k)}$  und am Decoderausgang   ⇒   $\underline{v}_j^{(k)}$,
  jeweils in Blöcken zu  $k$  Bit:

$${\rm Pr(Blockfehler)} = {\rm Pr} \left (\underline{\upsilon}_j^{(k)} \ne \underline{u}_j^{(k)} \right )\hspace{0.05cm}.$$

• Die  $\rm {Bitfehlerwahrscheinlichkeit}$  bezieht sich ebenfalls auf den Eingang und den Ausgang des betrachteten Codiersystems, allerdings auf Bitebene:

$${\rm Pr(Bitfehler)} = {\rm Pr} \left ({\upsilon}_{j,\hspace{0.05cm} i} \ne {u}_{j,\hspace{0.05cm} i} \right )\hspace{0.05cm}.$$

Hierbei ist vereinfachend vorausgesetzt, dass alle  $k$  Bit  $u_{j,\hspace{0.08cm}i}$  des Informationsblockes  $j$  mit gleicher Wahrscheinlichkeit verfälscht werden  $(1 ≤ i ≤ k)$. Andernfalls müsste über die  $k$  Bit noch gemittelt werden.

Zwischen der Blockfehler– und der Bitfehlerwahrscheinlichkeit besteht allgemein der Zusammenhang:

$$\frac{1}{k} \cdot {\rm Pr(Blockfehler)} \le {\rm Pr(Bitfehler)} \le {\rm Pr(Blockfehler)} \hspace{0.05cm}.$$

• Die untere Schranke ergibt sich, wenn bei allen fehlerhaften Blöcken alle Bit falsch sind.
• Gibt es in jedem fehlerhaften Block genau nur einen einzigen Bitfehler, dann ist die Bitfehlerwahrscheinlichkeit   ⇒   ${\rm Pr(Bitfehler)}$  identisch mit der Blockfehlerwahrscheinlichkeit   ⇒   ${\rm Pr(Blockfehler)}$.

Zur Definition verschiedener Fehlerwahrscheinlichkeiten

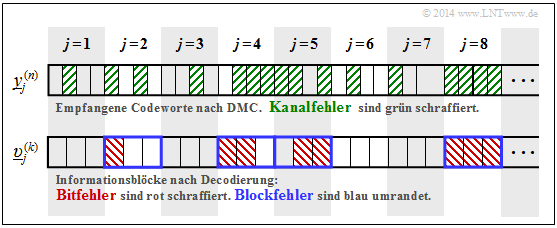
$\text{Beispiel 7:}$  Die Grafik zeigt oben die ersten acht Empfangsblöcke  $\underline{y}_j^{(n)}$  mit jeweils  $n = 4$ Bit.  Kanalfehler sind grün schraffiert.

Unten ist die Ausgangsfolge  $\underline{v}$  skizziert, unterteilt in Blöcke  $\underline{v}_j^{(k)}$  mit jeweils  $k = 3$  Bit:

• Bitfehler sind im unteren Diagramm rot schraffiert.
• Blockfehler erkennt man an der blauen Umrahmung.

Hierzu einige (aufgrund der kurzen Folge) nur sehr vage Angaben zu den Fehlerwahrscheinlichkeiten:

• Die Hälfte der Empfangsbits sind grün schraffiert. Daraus folgt:  

$${\rm Pr(Kanalfehler)} = 16/32 = 1/2.$$

• Die Bitfehlerwahrscheinlichkeit lautet mit der beispielhaften Codierung & Decodierung:  

$${\rm Pr(Bitfehler)} = 8/24 = 1/3.$$

• Dagegen würde bei uncodierter Übertragung gelten:  

$${\rm Pr(Bitfehler)} = {\rm Pr(Kanalfehler)} = 1/2.$$

• Die Hälfte der decodierten Blöcke sind blau umrandet. Daraus folgt:  

$${\rm Pr(Blockfehler)} = 4/8 = 1/2.$$

Mit  ${\rm Pr(Blockfehler)}= 1/2$  und  $k = 3$  liegt die Bitfehlerwahrscheinlichkeit in folgendem Bereich:  

$$1/6 \le {\rm Pr(Bitfehler)} \le 1/2 \hspace{0.05cm}.$$

• Die obere Schranke bezüglich Bitfehler ergibt sich, wenn in jedem der vier verfälschten Blöcke alle Bit falsch sind:   ${\rm Pr(Bitfehler)} = 12/24 = 1/2.$
• Die untere Schranke gibt an, dass in jedem der vier verfälschten Blöcke jeweils nur ein Bit falsch ist:   ${\rm Pr(Bitfehler)} = 4/24 = 1/6$.

Rate, Kanalkapazität und Bitfehlerwahrscheinlichkeit

Grundsätzlich gilt:

• Durch Kanalcodierung wird die Zuverlässigkeit  (englisch:  Reliability)  der Datenübertragung von der Quelle zur Sinke erhöht.
• Vermindert man die Coderate  $R = k/n$  und erhöht so die hinzugefügte Redundanz  $(1 - R)$, so wird im allgemeinen die Datensicherheit verbessert und damit die Bitfehlerwahrscheinlichkeit herabgesetzt, die wir im Weiteren kurz mit  $p_{\rm B}$  bezeichnen:

$$p_{\rm B} = {\rm Pr(Bitfehler)} = {\rm Pr} \left ({\upsilon}_{j,\hspace{0.05cm} i} \ne {u}_{j,\hspace{0.05cm} i} \right )\hspace{0.05cm}.$$

Das folgende Theorem basiert auf dem  Data Processing Theorem  und  Fano's Lemma.  Die Herleitung kann in den Standardwerken zur Informationstheorie nachgelesen werden, zum Beispiel in  [CT06]:

$\text{Umkehrung des Shannonschen Kanalcodierungstheorems:}$ 

Benutzt man zur Datenübertragung mit Rate  $R$  einen Kanal mit zu kleiner Kapazität  $C < R$, so kann die Bitfehlerwahrscheinlichkeit  $p_{\rm B}$  auch bei bestmöglicher Kanalcodierung eine untere Schranke nicht unterschreiten:

$$p_{\rm B} \ge H_{\rm bin}^{-1} \cdot \left ( 1 - {C}/{R}\right ) > 0\hspace{0.05cm}.$$

Hierbei bezeichnet  $H_{\rm bin}(⋅)$  die  binäre Entropiefunktion.

Da die Wahrscheinlichkeit der Blockfehler nie kleiner sein kann als die der Bitfehler,  ist für  $R > C$  auch die Blockfehlerwahrscheinlichkeit „Null” nicht möglich. 
Aus den angegebenen Schranken für die Bitfehler,

$$\frac {1}{k} \cdot {\rm Pr}({\rm Blockfehler}) \le {\rm Pr}({\rm Bitfehler}) \le {\rm Pr}({\rm Blockfehler})\hspace{0.05cm},$$

lässt sich auch ein Bereich für die Blockfehlerwahrscheinlichkeit angeben:

$$ {\rm Pr}({\rm Bitfehler}) \le {\rm Pr}({\rm Blockfehler}) \le k \cdot {\rm Pr}({\rm Bitfehler})\hspace{0.05cm}.$$

$\text{Beispiel 8:}$  Bei einem Kanal mit Kapazität  $C = 1/3$  (bit) ist eine fehlerfreie Datenübertragung   $(p_{\rm B} = 0)$  mit der Coderate  $R < 1/3$  prinzipiell möglich.

• Allerdings ist aus dem Kanalcodierungstheorem der spezielle  $(k$,  $n)$–Blockcode nicht bekannt, der dieses Wunschergebnis ermöglicht.  Auch Shannon macht hierzu keine Aussagen.
• Bekannt ist nur, dass ein solcher bestmöglicher Code mit unendlich langen Blöcken arbeitet.  Bei gegebener Coderate  $R = k/n$  gilt somit sowohl  $k → ∞$  als auch  $n → ∞$.
• Deshalb ist die Aussage  „Die Bitfehlerwahrscheinlichkeit ist Null”  nicht identisch mit  „Es treten keine Bitfehler auf”:   Auch bei endlich vielen Bitfehlern und  $k → ∞$  gilt nämlich  $p_{\rm B} = 0$.

Mit der Coderate  $R = 1 > C$  (uncodierte Übertragung) erhält man:

$$p_{\rm B} \ge H_{\rm bin}^{-1} \cdot \left ( 1 - \frac{1/3}{1}\right ) = H_{\rm bin}^{-1}(2/3) \approx 0.174 > 0\hspace{0.05cm}.$$

Mit der Coderate  $R = 1/2 > C$  ist die Bitfehlerwahrscheinlichkeit zwar kleiner,  aber ebenfalls von Null verschieden:

$$p_{\rm B} \ge H_{\rm bin}^{-1} \cdot \left ( 1 - \frac{1/3}{1/2}\right ) = H_{\rm bin}^{-1}(1/3) \approx 0.062 > 0\hspace{0.05cm}.$$

Aufgaben zum Kapitel

Aufgabe 3.10: Transinformation beim BSC

Aufgabe 3.10Z: BSC–Kanalkapazität

Aufgabe 3.11: Auslöschungskanal

Aufgabe 3.11Z: Extrem unsymmetrischer Kanal

Aufgabe 3.12: Streng symmetrische Kanäle

Aufgabe 3.13: Coderate und Zuverlässigkeit

Aufgabe 3.14: Kanalcodierungstheorem

Aufgabe 3.15: Data Processing Theorem