Definition and Properties of Reed-Solomon Codes

Coding principle and code parameters

A Reed–Solomon Code – hereafter sometimes shortened to RS code is a "linear block code" that is

Linear $(n, \, k)$ block code

an information block $\underline{u}$ with $k$ symbols.
assings a corresponding codeword $\underline{c}$ with $n > k$

symbols. These codes, still widely used today, were invented as early as the early 1960s by "Irving Stoy Reed" and "Gustave Solomon" .

In the chapter "Objective of Channel Coding" the information block was denoted by $\underline{u}= (u_1,$ ... , $u_k)$ and the codeword by $\underline{x}= (x_1,$ ... , $x_n)$ .

The nomenclature change $\underline{x} \to \underline{c}$ (see graphic) was made to eliminate confusion with the argument of polynomials and to simplify the description of RS codes.

All the properties of linear cyclic block codes mentioned in the section "linear codes and cyclic codes" also apply to a Reed–Solomon–code. In addition:

Construction and decoding of Reed–Solomon codes are based on the arithmetic of a Galois field ${\rm GF}(q)$, where we restrict ourselves here to binary extension fields with $q=2^m$ elements :

\[{\rm GF}(2^m) = \big \{\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} ,\hspace{0.05cm}\hspace{0.1cm} \alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm}\text{...}\hspace{0.1cm}, \alpha^{q-2}\hspace{0.05cm} \big \}\hspace{0.05cm}. \]

Principally different from the first chapter is that the coefficients $u_0$, $u_1$, ... , $u_{k-1}$ now no longer specify individual bits of information $(0$ or $1)$ but are also elements of ${\rm GF}(2^m)$ . Each of the $n$ symbols represents $m$ bits.

For Reed–Solomon codes, the parameter $n$ (code length) is always equal to the number of elements of the Galois field excluding the zero word: $n= q-1$.
We use the following nomenclature for this purpose:

\[{\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} = \big \{\hspace{0.05cm} \alpha^{0} ,\hspace{0.05cm}\hspace{0.1cm} \alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm}, \alpha^{n-1}\hspace{0.05cm} \big \}\hspace{0.05cm}. \]

The $k$ coefficients $u_i \in {\rm GF}(2^m)$ of the information block $\underline{u}$, where for the index $ 0 \le i < k$ holds, can also be formally expressed by a polynomial $u(x)$ . The degree of the polynomial is here $k-1$:

\[u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i} = u_0 + u_1 \cdot x + u_2 \cdot x^2 + \hspace{0.1cm}\text{...}\hspace{0.1cm}+ u_{k-1} \cdot x^{k-1} \hspace{0.05cm},\hspace{0.4cm} u_i \in {\rm GF}(2^m) \hspace{0.05cm}.\]

The $n$ symbols of the associated codeword $\underline{c}= (c_0, c_1,$ ... , $c_{n-1})$ result with this polynomial $u(x)$ to be

\[c_0 = u(\alpha^{0}) \hspace{0.05cm},\hspace{0.3cm} c_1 = u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm},\hspace{0.3cm} c_{n-1}= u(\alpha^{n-1}) \hspace{0.05cm}.\]

Mostly the code symbols $c_i \in {\rm GF}(2^m)$ are converted back to binary ⇒ ${\rm GF}(2)$ before transmission, where each symbol is then represented by $m$ bits.

We briefly summarize these statements:

$\text{Definition:}$ A $(n, k)$–Reed–Solomon code for the Galois field ${\rm GF}(2^m)$ is defined by.

the $n= 2^{m-1}$ elements of ${\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} =\{ \alpha^0, \alpha^1, \, \text{...} \, , \alpha^{n-1}\}$, where $\alpha$ denotes a "primitive element" of ${\rm GF}(2^m)$ denotes,

an information blockt $\underline{u}$ matched "polynomial" of degree $k-1$ the form

\[u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i} = u_0 + u_1 \cdot x + u_2 \cdot x^2 + \hspace{0.1cm}... \hspace{0.1cm}+ u_{k-1} \cdot x^{k-1} \hspace{0.05cm},\hspace{0.4cm} u_i \in {\rm GF}(2^m) \hspace{0.05cm}.\]

Thus, the $(n, k)$–Reed–Solomon code can be described as.

\[C_{\rm RS} = \Big \{ \underline {c} = \big ( u(\alpha^{0}) \hspace{0.05cm},\hspace{0.1cm} u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm}, u(\alpha^{n-1})\hspace{0.1cm} \big ) \hspace{0.1cm} \big \vert \hspace{0.2cm} u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i}\hspace{0.05cm},\hspace{0.2cm} u_i \in {\rm GF}(2^m) \Big \} \hspace{0.05cm}.\]

The previous information will now be illustrated by two simple examples.

$\rm GF(2^2)$ in three different representations:
Exponential, polynomial and coefficient form

$\text{Example 1:}$ We consider the following code parameters:

\[k = 2 \hspace{0.05cm},\hspace{0.15cm}n = 3 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \underline {u} = (u_0, u_1)\hspace{0.05cm},\hspace{0.15cm} \underline {c} = (c_0, c_1, c_2)\hspace{0.05cm},\]

\[q = n+1 = 4 \hspace{0.45cm} \Rightarrow \hspace{0.5cm} {\rm GF} (q) = {\rm GF} (2^m) \hspace{0.5cm} \Rightarrow \hspace{0.5cm} m = 2\hspace{0.05cm}.\]

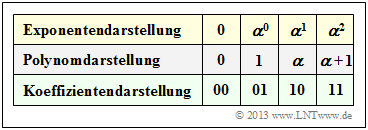
Starting from the conditional equation $p(\alpha) = \alpha^2 + \alpha + 1 = 0$ ⇒ $\alpha^2 = \alpha + 1$ one obtains the assignments between

the exponential representation,
the polynomial representation and
the coefficient representation

of ${\rm GF}(2^2)$ according to the above table. From this it can be seen:

The coefficient vector is expressed by the polynomial $u(x) = u_0 + u_1 \cdot x$ . The polynomial degree is $k- 1 = 1$.
For $u_0 = \alpha^1$ and $u_1 = \alpha^2$ we obtain, for example, the polynomial $u(x) = \alpha + \alpha^2 \cdot x$ and thus

\[c_0 = u (x = \alpha^0) = u (x = 1) = \alpha + \alpha^2 \cdot 1 = \alpha + (\alpha + 1) =1 \hspace{0.05cm},\]

\[c_1 =u (x = \alpha^1) = \alpha + \alpha^2 \cdot \alpha = \alpha + \alpha^3 = \alpha + \alpha^0 = \alpha + 1 = \alpha^2 \hspace{0.05cm},\]

\[c_2 =u (x = \alpha^2) = \alpha + \alpha^2 \cdot \alpha^2 = \alpha + \alpha^4 = \alpha + \alpha^1 = 0 \hspace{0.05cm}.\]

This results in the following assignments on symbol or bit level:

\[\underline {u} =(\alpha^1, \ \alpha^2)\hspace{0.57cm}\leftrightarrow\hspace{0.3cm} \underline {c} = (1, \ \alpha^2, \ 0)\hspace{0.05cm},\hspace{1cm}\underline {u}_{\rm bin} =(1,\ 0,\ 1,\ 1)\hspace{0.3cm}\leftrightarrow\hspace{0.3cm} \underline {c}_{\rm bin} = (0,\ 1,\ 1,\ 1,\ 0,\ 0)\hspace{0.05cm}.\]

Codetabelle des $\text{RSC (3, 2, 2)}_4$

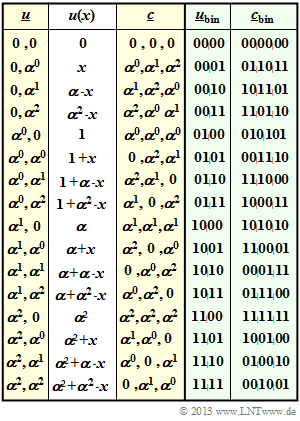
$\text{Example 2:}$ On the right is the code table of the $\text{RSC (3, 2, 2)}_4$ named Reed–Solomon code.

The label refers to the parameters $n=3$, $k=2$, $d_{\rm min}=2$ and $q = 4$.
In columns 1 to 3, one can see the relationship $\underline {u} \ → \ u(x) \ → \ \underline {c}$.
In the last two columns, the coding rule $\underline {u}_{\rm bin} \ ↔ \ \underline {c}_{\rm bin}$ is given.

For clarification again the entry for $(\alpha^0, \ \alpha^2)$:

\[u(x) = u_0 + u_1 \cdot x = \alpha^0 + \alpha^2 \cdot x. \]

This results in the following code symbols:

\[c_0 = u (x = \alpha^0) = 1 + \alpha^2 \cdot 1 = 1 + (1+\alpha ) =\alpha \hspace{0.05cm},\]

\[c_1 = u (x = \alpha^1) = 1 + \alpha^2 \cdot \alpha = 1 + (1+\alpha ) \cdot \alpha = 1 + \alpha + \alpha^2 = 0 \hspace{0.05cm},\]

\[c_2 =u (x = \alpha^2) = 1 + \alpha^2 \cdot \alpha^2 = 1 + \alpha = \alpha^2 \hspace{0.05cm}.\]

Hints:

From the element set $\{0, \ \alpha^0 = 1, \ \alpha^1 = \alpha, \ \alpha^2\}$ it should not be concluded that for this code the 3D–representation with axes $\alpha^0 = 1$, $\alpha^1 = \alpha$, $\alpha^2$ applies. See section "primitive polynomials" – example 5.
On the contrary, from the coefficient representation in $\text{Example 1}$ it is clear that ${\rm GF} (2^2)$ is two-dimensional, where the axes of the two dimensional representation are to be labeled $\alpha^0 = 1$ and $\alpha^1 = \alpha$ .

Generator matrix of Reed-Solomon codes

Since the Reed–Solomon code is a linear block code, the relationship between information word $\underline {u}$ and codeword $\underline {c}$ given by the "Generator Matrix" $\boldsymbol{\rm G}$ :

\[\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.\]

As with any linear $(n, k)$–block code, the generator matrix consists of $k$ rows and $n$ columns. In contrast to the chapter "General Description of Linear Block Codes" however, now the elements of the generator matrix are no longer binary $(0$ or $1)$, but come from the Galois field ${\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} $.

$\text{Example 3:}$ We consider as in $\text{Example 2}$ (previous page) the $\text{RSC (3, 2, 2)}_4$ whose generator matrix has the following form:

\[ { \boldsymbol{\rm G} } = \begin{pmatrix} g_{00} & g_{01} & g_{02}\\ g_{10} & g_{11} & g_{12} \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} g_{ij} \in {\rm GF}(2^2) \hspace{-0.01cm}\setminus \hspace{-0.01cm} \{0\} = \big \{\hspace{0.05cm} \alpha^{0} \hspace{0.05cm},\hspace{0.1cm} \alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} \hspace{0.05cm}\big \}\hspace{0.05cm}. \]

Beside this:

The first row of $\boldsymbol{\rm G}$ gives the codeword for the information word $\underline {u}_1 = (1, 0)$ respectively for the polynomial function $u_1(x) = 1$. Thus one receives the matrix elements of the first row

\[g_{00} = u_{1}(\alpha^{0}) = 1\hspace{0.05cm},\hspace{0.3cm} g_{01} = u_{1}(\alpha^{1}) = 1\hspace{0.05cm},\hspace{0.3cm} g_{02} = u_{1}(\alpha^{2}) = 1\hspace{0.05cm}.\]

The second row is equal to the code word for the information word $\underline {u}_2 = (0, 1)$ ⇒ $u_2(x) = x$. Thus, the matrix elements of the second row are:

\[g_{10} = u_{2}(\alpha^{0}) = \alpha^{0} = 1\hspace{0.05cm},\hspace{0.3cm} g_{11} = u_{2}(\alpha^{1}) = \alpha \hspace{0.05cm},\hspace{0.3cm} g_{12} = u_{2}(\alpha^{2}) = \alpha^{2}\hspace{0.05cm}.\]

\[\Rightarrow\hspace{0.3cm} { \boldsymbol{\rm G} } = \begin{pmatrix} 1 & 1 & 1\\ 1 & \alpha & \alpha^2 \end{pmatrix}\hspace{0.05cm}.\]

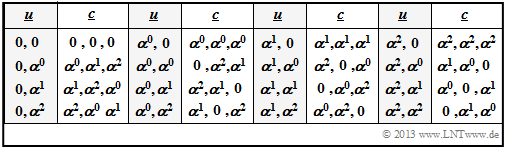
For the information word $\underline {u}= (u_0, \ u_1)$ mit den Symbolen $u_0, \ u_1 ∈ \{0, \ \alpha^0, \ \alpha^1 = \alpha, \ \alpha^2\}$ one obtains, considering the two equations $\alpha^2 = \alpha + 1$ and $\alpha^3 = \alpha^0 = 1$ again the code table of the $\text{RSC (3, 2, 2)}_4$ at symbol level.

Code table of the $\text{RSC (3, 2, 2)}_4$ at symbol level

Of course, with the generator matrix you get exactly the same code table $\underline {u} ↔ \underline {c}$ as after the calculation via the function $u(x)$.
The corresponding code table on bit level (see $\text{Example 2}$ on the previous page) results again, if the elements are not given in exponent representation, but in coefficient form:

\[(0, \hspace{0.1cm}\alpha^{0}, \hspace{0.1cm}\alpha^{1}, \hspace{0.1cm}\alpha^{2}) \hspace{0.3cm}\Leftrightarrow\hspace{0.3cm}(00, \hspace{0.1cm}01, \hspace{0.1cm}10, \hspace{0.1cm}11) \hspace{0.05cm}. \]

Generator matrix and parity-check matrix

We now generalize the result of the last page for a Reed–Solomon code with

the dimension $k$ (number of symbols per information block),

the codeword length $n$ (number of symbols per codeword).

"generator matrix" $\boldsymbol{\rm G}$ $(k$ rows, $n$ columns$)$ and "parity-check matrix" $\boldsymbol{\rm H}$ $(n-k$ rows, $n$ columns$)$ must jointly satisfy the following equation:

\[{ \boldsymbol{\rm G}} \cdot { \boldsymbol{\rm H }}^{\rm T}= { \boldsymbol{\rm 0}}\hspace{0.05cm}.\]

Here, $\boldsymbol{\rm 0}$ denotes a zero matrix $($all elements equal $0)$ with $k$ rows and $n-k$ columns.

$\text{Example 4:}$ We consider the $\text{RSC (7, 3, 5)}_8$ ⇒ code parameter $n= 7$, $k= 3$, based on the Galois field $\rm GF(2^3 = 8)$ with the constraint $\alpha^3 =\alpha + 1$. Note with respect to the code name:

The third parameter of the nomenclature commonly used for block codes names the free distance $d_{\rm min}= 5$.

Unlike the binary codes discussed in the chapter "Examples of binary block codes" (single parity-check code, repetition code, Hamming code), the Reed–Solomon codes still have the hint $q$ added to the Galois field $($here: $q = 8)$.

All elements of the generator matrix and the parity-check matrix,

\[{ \boldsymbol{\rm G} } = \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5} \end{pmatrix}\hspace{0.05cm},\hspace{0.4cm} { \boldsymbol{\rm H} } = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4}\\ 1 & \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2} & \alpha^{6} & \alpha^{3} \end{pmatrix}\hspace{0.05cm}, \]

originate from the Galois field ${\rm GF}(2^3) \hspace{-0.01cm}\setminus \hspace{-0.01cm} \{0\} = \big \{\hspace{0.05cm} \alpha^{0} \hspace{0.05cm},\hspace{0.1cm}\alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} \hspace{0.05cm},\hspace{0.1cm} \alpha^{3} \hspace{0.05cm},\hspace{0.1cm}\alpha^{4}\hspace{0.05cm},\hspace{0.1cm} \alpha^{5} \hspace{0.05cm},\hspace{0.1cm} \alpha^{6} \hspace{0.05cm}\big \}$. For the matrix product holds:

\[{ \boldsymbol{\rm G} } \cdot { \boldsymbol{\rm H } }^{\rm T}= \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5} \end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4\\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1\\ \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5}\\ \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2}\\ \alpha^5 & \alpha^{3} & \alpha^{1} & \alpha^{6}\\ \alpha^6 & \alpha^{5} & \alpha^{4} & \alpha^{3} \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \hspace{0.05cm}.\]

This will be demonstrated here for two elements only:

First row, first column:

\[1 \hspace{0.1cm} \cdot \hspace{0.1cm} \big [1 + \alpha^1 + \alpha^2 + \alpha^3 + \alpha^4 + \alpha^5 + \alpha^6 \big ] = 1 + \alpha + \alpha^2 + (\alpha + 1) + (\alpha^2 + \alpha)+ (\alpha^2 + \alpha +1)+ (\alpha^2 + 1) = 0 \hspace{0.05cm}; \]

Last row, last column:

\[1 \hspace{0.1cm} \cdot \hspace{0.1cm} 1 + \alpha^2 \cdot \alpha^4 + \alpha^4 \cdot \alpha^1 + \alpha^6 \cdot \alpha^5+ \alpha^1 \cdot \alpha^2+ \alpha^3 \cdot \alpha^6+ \alpha^5 \cdot \alpha^3= 1 + \alpha^6 + \alpha^5 + \alpha^{11} + \alpha^{3}+ \alpha^{9}+ \alpha^{8} =\]

\[ \hspace{1.5cm} = \hspace{0.15cm} 1 + \alpha^6 + \alpha^5 + \alpha^{4} + \alpha^{3}+ \alpha^{2}+ \alpha^{1} =0 \hspace{0.05cm}.\]

Singleton bound and minimum distance

Eine wichtige Kenngröße eines jeden Blockcodes ist die minimale Distanz zwischen zwei beliebigen Codeworten $\underline {c}_i$ und $\underline {c}_j$.

Die Reed–Solomon–Codes gehören zur Klasse der linearen und zyklischen Codes. Bei diesen kann man vom Nullwort $\underline {c}_0 = (0, 0, \hspace{0.05cm} \text{...} \hspace{0.05cm}, 0)$ als Bezugsgröße ausgehen.
Aus der Anzahl der Nullen in den anderen Codeworten $\underline {c}_j ≠ \underline {c}_0$ lässt sich das Distanzspektrum $\{ \hspace{0.05cm}W_j\hspace{0.05cm}\}$ angeben.

$\text{Beispiel 5:}$ Die Tabelle verdeutlicht die Bestimmung des Distanzspektrums für den $\text{RSC (3, 2, 2)}_4$.

Gegenüber den bisherigen Grafiken wird die Symbolmenge vereinfachend mit $\{0,\ 1,\ 2,\ 3\}$ anstelle von $\{0,\ \alpha^0,\ \alpha^1,\ \alpha^2\}$ bezeichnet.
Die Distanz $d$ zwischen $\underline {c}_j$ und dem Nullwort $\underline {c}_0$ ist identisch dem Hamming–Gewicht $w_{\rm H}(\underline {c}_j)$.

Zur Herleitung des Distanzspektrums für den $\text{RSC (3, 2, 2)}_4$

Aus der oberen Tabelle kann unter anderem abgelesen werden:

Neun Codeworte unterscheiden sich vom Nullwort in zwei Symbolen und sechs Codeworte in drei Symbolen: $W_2 = 9$, $W_3 = 6$.
Es gibt kein einziges Codewort mit nur einer Null. Das heißt: Die minimale Distanz beträgt hier $d_{\rm min} = 2$.

Aus der unteren Tabelle erkennt man, dass auch für die Binärdarstellung $d_{\rm min} = 2$ gilt.

Dieses empirische Ergebnis soll nun verallgemeinert werden:

$\text{Ohne Beweis:}$

Die minimale Distanz eines jeden $(n, k)$–Reed–Solomon–Codes ist $d_{\rm min} =n-k+1$ ⇒ es lassen sich $e = d_{\rm min} -1 =n-k$ Symbolfehler erkennen.

Bei fehlerkorrigierenden Codes wählt man meist $d_{\rm min} $ ungeradzahlig ⇒ $n-k$ geradzahlig. Bei RS–Codes können dann bis zu $t =(n-k)/2$ Symbolfehler korrigiert werden.

Die Singleton–Schranke besagt, dass für alle linearen Codes $d_{\rm min} \le n-k+1$ gilt. RS–Codes erreichen diese Schranke mit Gleichheit; sie sind so genannte MDS–Codes (Maximum Distance Separable ).

Das Distanzspektrum setzt sich zusammen aus $W_0 = 1$ sowie weiteren Gewichtsfaktoren $W_i$ mit $d ≤ i ≤ n$, wobei in der folgenden Gleichung $d_{\rm min}$ mit $d$ abgekürzt ist:

\[W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \bigg [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \bigg ]\hspace{0.05cm}.\]

Codebezeichnung und Coderate

Die übliche Bezeichnung für die Reed–Solomon–Codes ist ${\rm RSC} \ \ (n,\ k, \ d_{\rm min})_q$ mit

der Länge $n$ des Codes (Symbolanzahl eines Codewortes),

der Dimension $k$ des Codes (Symbolanzahl eines Informationswortes),

der minimalen Distanz $d_{\rm min} = n-k+1$, maximal entsprechend der Singleton–Schranke, und

der Größe $q = 2^m$ des Galoisfeldes ${\rm GF}(q)$.

Alle Elemente $u_i$ des Informationswortes $\underline{u}= (u_0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_{k-1})$ und alle Elemente c_i des Codewortes $\underline{c}= (c_0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, c_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, c_{n-1})$ sind nicht binäre Symbole und entstammen dem Galoisfeld ${\rm GF}(q)$.

Für die Realisierung werden diese Symbole stets auch binär dargestellt und man kommt zum äquivalenten binären Reed–Solomon–Code ${\rm RSC} \ \ (n_{\rm bin},\ k_{\rm bin}, \ d_{\rm min})_2$ mit

$n_{\rm bin} = n \cdot m$ Bit eines Codewortes,

$k_{\rm bin} = k \cdot m$ Bit eines Informationswortes.

Die Coderate wird durch diese Maßnahme nicht verändert:

\[R_{\rm bin} = \frac{k_{\rm bin}}{n_{\rm bin}} = \frac{k \cdot m}{n \cdot m} = \frac{k}{n} = R \hspace{0.05cm}.\]

Ebenso ändert sich durch den Übergang von ${\rm GF}(q)$ auf ${\rm GF}(2)$ nichts an der minimalen Distanz $d_{\rm min}$.

$\text{Beispiel 6:}$ Wie im $\text{Beispiel 5}$ (vorherige Seite) betrachten wir wieder den $\text{RSC (3, 2, 2)}_4$ und geben dessen Distanzspektrum $\{ \hspace{0.05cm}W_j\hspace{0.05cm}\}$ nochmals an (obere Tabelle). Die untere Tabelle gilt für den äquivalenten binären Reed–Solomon–Code $\text{RSC (6, 4, 2)}_2$.

Herleitung der Distanzspektren von $\text{RSC (3, 2, 2)}_4$ und $\text{RSC (6, 4, 2)}_2$

Beide Codes haben die gleiche Coderate $R = k/n =2/3$ und auch die gleiche minimale Distanz $d_{\rm min} = 2$.
Die beiden Codes unterscheiden sich jedoch hinsichtlich des Distanzspektrums $\{ \hspace{0.05cm}W_j\hspace{0.05cm}\}$ und der Gewichtsfunktion $W(X)$:

$$\text{RSC (3, 2, 2)}_4\text{:} \hspace{0.3cm} W_0 = 1\hspace{0.05cm}, \hspace{0.2cm}W_2 = 9\hspace{0.05cm}, \hspace{0.2cm}W_3 = 6\hspace{0.3cm}\Rightarrow\hspace{0.3cm}W(X) = 1 + 9 \cdot X^2 + 6 \cdot X^3\hspace{0.05cm}.$$

$$\text{RSC (6, 4, 2)}_2\text{:} \hspace{0.3cm} W_0 = 1\hspace{0.05cm}, \hspace{0.2cm}W_2 = 3\hspace{0.05cm}, \hspace{0.2cm}W_3 = 8 \hspace{0.05cm}, \hspace{0.2cm}W_4 = 3\hspace{0.05cm}, \hspace{0.2cm}W_6 = 1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm}W(X) = 1 + 3 \cdot X^2 + 8 \cdot X^3 + 4 \cdot X^4 + X^6 \hspace{0.05cm}.$$

Bedeutung der Reed–Solomon–Codes

Anhand des hier oft beispielhaft betrachteten $\text{RSC (3, 2, 2)}_4$ konnten wir viele Eigenschaften der Reed–Solomon–Codes in überschaubarem Rahmen kennenlernen. Praxisrelevant ist dieser Code allerdings nicht, da wegen $d_{\rm min} = 2$ kein einziger Fehler korrigiert und auch nur ein einziger Fehler erkannt werden kann. Schon der nächstgrößere Code $\text{RSC (7, 3, 5)}_8$, der bis zu $t = 2$ Fehler korrigieren kann, weist bereits eine Codetabelle mit $8^3 = 512$ Einträgen auf und ist zu Demonstrationszwecken ungeeignet.

In der Praxis werden meist sehr große RS–Codes eingesetzt, zum Beispiel der $\text{RSC (255, 223, 33)}_{256}$ mit folgenden Eigenschaften:

Der Code basiert auf dem Galoisfeld $\rm GF(2^8)$. Jedes Symbol entspricht somit einem Byte. Die Coderate ist mit $R = 0.8745$ relativ groß.

Trotz dieser großen Coderate (also geringe Redundanz) können mit diesem Code bis zu $e = 32$ Fehler innerhalb eines Blocks aus $255$ Symbolen erkannt und $t = 16$ Fehler korrigiert werden.

Die Codetabelle würde allerdings $2^{8 \hspace{0.05cm}\cdot \hspace{0.05cm} 223}= 2^{ \hspace{0.05cm} 1784} ≈ 10^{537}$ Einträge aufweisen und wird deshalb wahrscheinlich auch von niemanden tatsächlich erstellt.

Der große Vorteil der Reed–Solomon–Codes (und einer ganzen Reihe davon abgeleiteter weiterer Codes) ist zum einen, dass sie analytisch geschlossen konstruiert werden können, zum anderen ihre große Flexibilität hinsichtlich der Codeparameter. Meist geht man wie folgt vor:

Man gibt die Korrekturfähigkeit in Form des Parameters $t$ vor. Daraus ergibt sich die minimale Distanz $d_{\rm min} = 2t + 1$ und die Differenz $n-k = 2t$ entsprechend der Singleton–Schranke. Einen besseren Wert gibt es nicht.

Ein weiterer Entwurfsparameter ist die Coderate $R=k/n$, wobei die Codewortlänge $n = 2^m -1$ nicht völlig frei wählbar ist. Durch Erweiterung, Verkürzung und Punktierung – siehe Aufgabe 1.9Z – kann die Vielzahl an möglichen Codes weiter vergrößert werden.

Bei Reed–Solomon–Codes ist die Gewichtsverteilung exakt bekannt und es ist eine Anpassung an die Fehlerstruktur des Kanals möglich. Diese Codes sind insbesondere für Bündelfehlerkanäle gut geeignet, die bei mobilen Funksystemen aufgrund von temporären Abschattungen häufig vorliegen.

Im Falle statistisch unabhängiger Fehler sind BCH–Codes (von $\rm B$ose–$\rm C$haudhuri–$\rm H$ocquenghem) besser geeignet. Diese sind mit den RS–Codes eng verwandt, allerdings erfüllen sie nicht immer das Singleton–Kriterium. Eine ausführliche Beschreibung finden Sie in [Fri96]^[1].

Die Decodierung nach dem BDD–Prinzip (Bounded Distance Decoding ) kann rechentechnisch sehr einfach erfolgen, zum Beispiel mit dem Berlekamp–Massey–Algorithmus. Zudem kann der Decoder ohne großen Mehraufwand auch Soft Decision Information verarbeiten.