Exercise 3.7: Comparison of Two Convolutional Encoders

• Return to book

Two convolutional encoders with parameters  $n = 2, \ k = 1, \ m = 2$

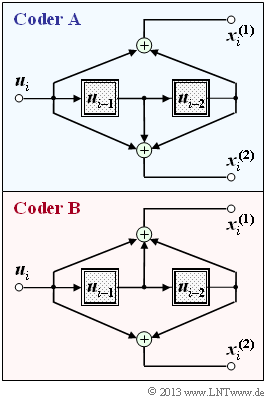
The graph shows two rate $1/2$ convolutional encoders, each with memory  $m = 2$:

• The coder  $\rm A$  has the transfer function matrix $\mathbf{G}(D) = (1 + D^2, \ 1 + D + D^2)$.
• In the coder  $\rm B$  the two filters (top and bottom) are interchanged, and it holds : $\mathbf{G}(D) = (1 + D + D^2, \ 1 + D^2)$.

The lower encoder  $\rm B$  has already been treated in detail in the theory part.

In the present exercise, you are to first determine the state transition diagram for coder  $\rm A$  and then work out the differences and the similarities between the two state diagrams.

Hints:

• This exercise belongs to the chapter  "Code description with state– and trellis diagram".
• Reference is made in particular to the sections.
  •   "State definition for a memory register"  and.
  •   "Representation in the state transition diagram".

Questions

1

  $\underline{u} = (0, \, 1, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$ holds. Which sequences does Coder  $\rm A$ generate?

	$\underline{x}^{(1)} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$,
	$\underline{x}^{(1)} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$,
	$\underline{x}^{(2)} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$,
	$\underline{x}^{(2)} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$.

2

Which of the above state transitions exist in encoder  $\rm A$?

	$s_i = S_0, \ u_i = 0 \ ⇒ \ s_{i+1} = S_0; \hspace{1cm} s_i = S_0, \ u_i = 1 \ ⇒ \ s_{i+1} = S_1$.
	$s_i = S_1, \ u_i = 0 \ ⇒ \ s_{i+1} = S_2; \hspace{1cm} s_i = S_1, \ u_i = 1 \ ⇒ \ s_{i+1} = S_3$.
	$s_i = S_2, \ u_i = 0 \ ⇒ \ s_{i+1} = S_0; \hspace{1cm} s_i = S_2, \ u_i = 1 \ ⇒ \ s_{i+1} = S_1$.
	$s_i = S_3, \ u_i = 0 \ ⇒ \ s_{i+1} = S_2; \hspace{1cm} s_i = S_3, \ u_i = 1 \ ⇒ \ s_{i+1} = S_3$.

3

How do the two state transition diagrams differ?

	Other state transitions are possible.
	All eight transitions have different code sequences.
	Differences exist only for the code sequences  $(01)$  and  $(10)$.

Solution

Solution

Calculation of the code sequence

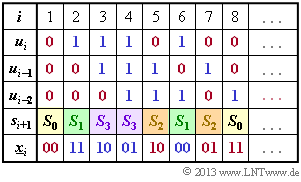
(1)  The calculation is based on the equations.

$$x_i^{(1)} = u_i + u_{i–2},$$

$$x_i^{(2)} = u_i + u_{i–1} + u_{i–2}.$$

• Initially, the two memories ($u_{i–1}$ and $u_{i–2}$) are preallocated with zeros  ⇒  $s_1 = S_0$.
• With $u_1 = 0$, we get $\underline{x}_1 = (00)$ and $s_2 = S_0$.
• With $u_2 = 1$ one obtains the output $\underline{x}_2 = (11)$ and the new state $s_3 = S_3$.

From the adjacent calculation scheme one recognizes the correctness of the proposed solutions 1 and 4.

State transition diagram of encoder  $\rm A$

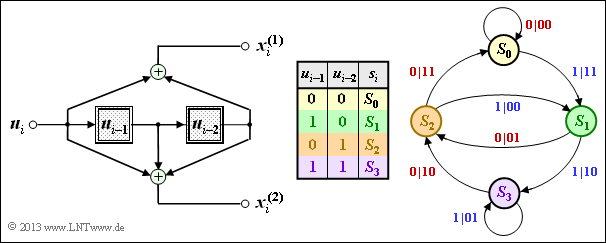
(2)  All proposed solutions are correct:

• This can be seen by evaluating the table at (1).
• The results are shown in the adjacent graph.

State transition diagram of encoder  $\rm B$

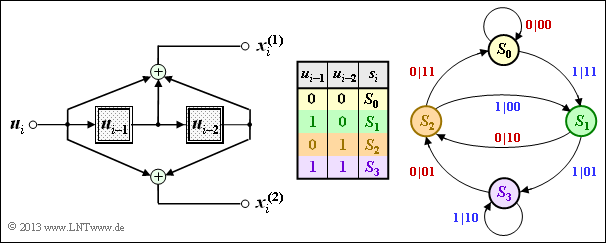
(3)  Correct is only statement 3:

• The state transition diagram of Coder  $\rm B$  is sketched on the right. For derivation and interpretation, see section "Representation in the state transition diagram".
• If we swap the two output bits $x_i^{(1)}$ and $x_i^{(2)}$, we get from the convolutional encoder  $\rm A$  to the convolutional encoder  $\rm B$  (and vice versa).