Definition and Properties of Reed-Solomon Codes

Coding principle and code parameters

A "Reed–Solomon code" – hereafter sometimes shortened to "RS code" – is a "linear block code" which assigns

an information block $\underline{u}$ with $k$ symbols

to a corresponding code word $\underline{c}$ with $n > k$ symbols.

Linear $(n, \, k)$ block code with new nomenclature

These codes, still widely used today, were invented as early as the early 1960s

by Irving Stoy Reed

and Gustave Solomon.

In the chapter "Objective of Channel Coding"

the information block was denoted by $\underline{u}= (u_1,$ ... , $u_k)$ and

the code word by $\underline{x}= (x_1,$ ... , $x_n)$.

The nomenclature change $\underline{x} \to \underline{c}$ $($see graphic$)$ was made to eliminate confusion with the argument of polynomials and to simplify the description of Reed–Solomon codes.

All the properties of linear cyclic block codes mentioned in the section "Linear codes and cyclic codes" also apply to the Reed–Solomon codes. In addition:

Construction and decoding of Reed–Solomon codes are based on the arithmetic of a Galois field ${\rm GF}(q)$, where we restrict ourselves here to binary extension fields with $q=2^m$ elements;:

\[{\rm GF}(2^m) = \big \{\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} ,\hspace{0.05cm}\hspace{0.1cm} \alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm}\text{...}\hspace{0.1cm}, \alpha^{q-2}\hspace{0.05cm} \big \}\hspace{0.05cm}. \]

Principally different from the first chapter is that the coefficients $u_0$, $u_1$, ... , $u_{k-1}$ now no longer specify individual bits of information $(0$ or $1)$ but they are also elements of ${\rm GF}(2^m)$. Each of the $n$ symbols represents $m$ bits.

For Reed–Solomon codes, the parameter $n$ ("code length") is always equal to the number of elements of the Galois field excluding the zero word: $n= q-1$.
We use for this purpose the following nomenclature:

\[{\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} = \big \{\hspace{0.05cm} \alpha^{0} ,\hspace{0.05cm}\hspace{0.1cm} \alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm}, \alpha^{n-1}\hspace{0.05cm} \big \}\hspace{0.05cm}. \]

The $k$ coefficients $u_i \in {\rm GF}(2^m)$ of the information block $\underline{u}$, where for the index $ 0 \le i < k$ holds, can also be formally expressed by a polynomial $u(x)$. The degree of this polynomial is $k-1$:

\[u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i} = u_0 + u_1 \cdot x + u_2 \cdot x^2 + \hspace{0.1cm}\text{...}\hspace{0.1cm}+ u_{k-1} \cdot x^{k-1} \hspace{0.05cm},\hspace{0.4cm} u_i \in {\rm GF}(2^m) \hspace{0.05cm}.\]

The $n$ symbols of the associated code word $\underline{c}= (c_0, c_1,$ ... , $c_{n-1})$ result with this polynomial $u(x)$ to be

\[c_0 = u(\alpha^{0}) \hspace{0.05cm},\hspace{0.3cm} c_1 = u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm},\hspace{0.3cm} c_{n-1}= u(\alpha^{n-1}) \hspace{0.05cm}.\]

Mostly the code symbols $c_i \in {\rm GF}(2^m)$ are converted back to binary ⇒ ${\rm GF}(2)$ before transmission, where each symbol is then represented by $m$ bits.

We briefly summarize these statements:

$\text{Definition:}$ An $(n, k)\text{ Reed–Solomon code}$ for the Galois field ${\rm GF}(2^m)$ is defined by

the $n= 2^{m-1}$ elements of ${\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} =\{ \alpha^0, \alpha^1, \, \text{...} \, , \alpha^{n-1}\}$, where $\alpha$ denotes a "primitive element" of ${\rm GF}(2^m)$,

a "polynomial" of degree $k-1$ matched to an information block $\underline{u}$:

\[u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i} = u_0 + u_1 \cdot x + u_2 \cdot x^2 + \hspace{0.1cm}... \hspace{0.1cm}+ u_{k-1} \cdot x^{k-1} \hspace{0.05cm},\hspace{0.4cm} u_i \in {\rm GF}(2^m) \hspace{0.05cm}.\]

⇒ Thus, the $(n,\ k)$ Reed–Solomon code can be described as follows:

\[C_{\rm RS} = \Big \{ \underline {c} = \big ( u(\alpha^{0}) \hspace{0.05cm},\hspace{0.1cm} u(\alpha^{1})\hspace{0.05cm},\hspace{0.1cm}...\hspace{0.1cm}, u(\alpha^{n-1})\hspace{0.1cm} \big ) \hspace{0.1cm} \big \vert \hspace{0.2cm} u(x) = \sum_{i = 0}^{k-1} u_i \cdot x^{i}\hspace{0.05cm},\hspace{0.2cm} u_i \in {\rm GF}(2^m) \Big \} \hspace{0.05cm}.\]

The previous information will now be illustrated by two simple examples.

$\text{Example 1:}$ We consider the following code parameters:

$\rm GF(2^2)$ in three different representations:
Exponential, polynomial and coefficient form Korrektur

\[k = 2 \hspace{0.05cm},\hspace{0.15cm}n = 3 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \underline {u} = (u_0,\ u_1)\hspace{0.05cm},\hspace{0.15cm} \underline {c} = (c_0,\ c_1,\ c_2)\hspace{0.05cm},\]

\[q = n+1 = 4 \hspace{0.45cm} \Rightarrow \hspace{0.5cm} {\rm GF} (q) = {\rm GF} (2^m) \hspace{0.5cm} \Rightarrow \hspace{0.5cm} m = 2\hspace{0.05cm}.\]

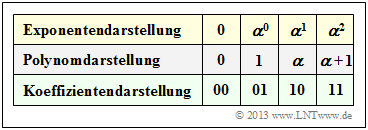
Starting from the conditional equation

$$p(\alpha) = \alpha^2 + \alpha + 1 = 0 \hspace{0.3cm} ⇒ \hspace{0.3cm} \alpha^2 = \alpha + 1,$$

one obtains the assignments between

the exponential representation,

the polynomial representation and

the coefficient representation

of ${\rm GF}(2^2)$ according to the above table. From this it can be seen:

The coefficient vector is expressed by the polynomial $u(x) = u_0 + u_1 \cdot x$. The polynomial degree is $k- 1 = 1$.
For $u_0 = \alpha^1$ and $u_1 = \alpha^2$ we obtain e.g. the polynomial $u(x) = \alpha + \alpha^2 \cdot x$ and thus

\[c_0 = u (x = \alpha^0) = u (x = 1) = \alpha + \alpha^2 \cdot 1 = \alpha + (\alpha + 1) =1 \hspace{0.05cm},\]

\[c_1 =u (x = \alpha^1) = \alpha + \alpha^2 \cdot \alpha = \alpha + \alpha^3 = \alpha + \alpha^0 = \alpha + 1 = \alpha^2 \hspace{0.05cm},\]

\[c_2 =u (x = \alpha^2) = \alpha + \alpha^2 \cdot \alpha^2 = \alpha + \alpha^4 = \alpha + \alpha^1 = 0 \hspace{0.05cm}.\]

⇒ This results in the following assignments on symbol or bit level:

$$\underline {u} =(\alpha^1, \ \alpha^2)\hspace{0.57cm}\leftrightarrow\hspace{0.3cm} \underline {c} = (1, \ \alpha^2, \ 0)\hspace{0.05cm},$$

$$\underline {u}_{\rm bin} =(1,\ 0,\ 1,\ 1)\hspace{0.3cm}\leftrightarrow\hspace{0.3cm} \underline {c}_{\rm bin} = (0,\ 1,\ 1,\ 1,\ 0,\ 0)\hspace{0.05cm}.$$

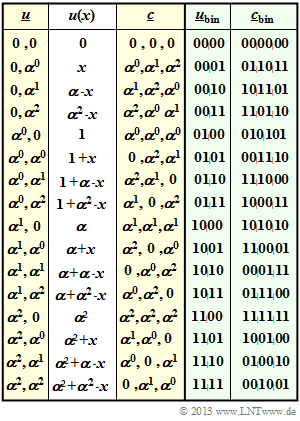
$\text{Example 2:}$ On the right you see the code table of a special Reed–Solomon code named $\text{RSC (3, 2, 2)}_4$.

Code table of the $\text{RSC (3, 2, 2)}_4$

The label refers to the parameters $n=3$, $k=2$, $d_{\rm min}=2$ and $q = 4$.

In columns 1 to 3, one can see the relationship $\underline {u} \ → \ u(x) \ → \ \underline {c}$.

In the last two columns, the coding rule $\underline {u}_{\rm bin} \ ↔ \ \underline {c}_{\rm bin}$ is given.

⇒ For clarification the entry for $(\alpha^0, \ \alpha^2)$:

\[u(x) = u_0 + u_1 \cdot x = \alpha^0 + \alpha^2 \cdot x. \]

This results in the following code symbols (see red mark):

\[c_0 = u (x = \alpha^0) = 1 + \alpha^2 \cdot 1 = 1 + (1+\alpha ) =\alpha \hspace{0.05cm},\]

\[c_1 = u (x = \alpha^1) = 1 + \alpha^2 \cdot \alpha = 1 + (1+\alpha ) \cdot \alpha = 1 + \alpha + \alpha^2 = 0 \hspace{0.05cm},\]

\[c_2 =u (x = \alpha^2) = 1 + \alpha^2 \cdot \alpha^2 = 1 + \alpha = \alpha^2 \hspace{0.05cm}.\]

Hints:

From the element set $\{0, \ \alpha^0 = 1, \ \alpha^1 = \alpha, \ \alpha^2\}$ it should not be concluded that for this code the three-dimensional representation with axes $\alpha^0 = 1$, $\alpha^1 = \alpha$, $\alpha^2$ applies. See section "Primitive Polynomials" – Example 5.

On the contrary, from the coefficient representation in $\text{Example 1}$ it is clear that ${\rm GF} (2^2)$ is two-dimensional, where the axes of the two dimensional representation are to be labeled $\alpha^0 = 1$ and $\alpha^1 = \alpha$.

Generator matrix of Reed-Solomon codes

Since the Reed–Solomon code is a linear block code, the relationship between the information word $\underline {u}$ and the code word $\underline {c}$ is given by the "generator matrix" $\boldsymbol{\rm G}$:

\[\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.\]

As with any linear $(n, k)$ block code, the generator matrix consists of

$k$ rows and
$n$ columns.

In contrast to the chapter "General Description of Linear Block Codes"

now the elements of the generator matrix are no longer binary $(0$ or $1)$,

but come from the Galois field ${\rm GF}(2^m) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\} $.

{{GraueBox|TEXT= $\text{Example 3:}$ We consider as in [[Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes#Coding_principle_and_code_parameters|$\text{Example 2}$ (see previous page) the $\text{RSC (3, 2, 2)}_4$ whose generator matrix has the following form:

\[ { \boldsymbol{\rm G} } = \begin{pmatrix} g_{00} & g_{01} & g_{02}\\ g_{10} & g_{11} & g_{12} \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} g_{ij} \in {\rm GF}(2^2) \hspace{-0.01cm}\setminus \hspace{-0.01cm} \{0\} = \big \{\hspace{0.05cm} \alpha^{0} \hspace{0.05cm},\hspace{0.1cm} \alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} \hspace{0.05cm}\big \}\hspace{0.05cm}. \]

Beside this:

The first row of $\boldsymbol{\rm G}$ gives the code word for the information word $\underline {u}_1 = (1,\ 0)$ respectively for the polynomial function $u_1(x) = 1$. Thus one receives the matrix elements of the first row

$$g_{00} = u_{1}(\alpha^{0}) = 1\hspace{0.05cm},$$

$$g_{01} = u_{1}(\alpha^{1}) = 1\hspace{0.05cm},$$

$$g_{02} = u_{1}(\alpha^{2}) = 1\hspace{0.05cm}.$$

The second row is equal to the code word for the information word $\underline {u}_2 = (0,\ 1)$ ⇒ $u_2(x) = x$. Thus, the matrix elements of the second row are:

$$g_{10} = u_{2}(\alpha^{0}) = \alpha^{0} = 1\hspace{0.05cm},$$

$$g_{11} = u_{2}(\alpha^{1}) = \alpha \hspace{0.05cm},$$

$$g_{12} = u_{2}(\alpha^{2}) = \alpha^{2}\hspace{0.05cm}.$$

So the complete generator matrix is:

$$ { \boldsymbol{\rm G} } = \begin{pmatrix} 1 & 1 & 1\\ 1 & \alpha & \alpha^2 \end{pmatrix}\hspace{0.05cm}.$$

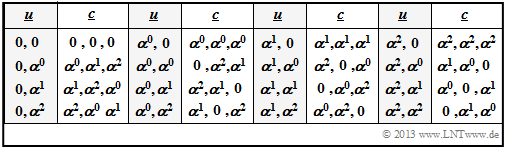
Code table of the $\text{RSC (3, 2, 2)}_4$ at symbol level

For the information word $\underline {u}= (u_0, \ u_1)$ with symbols

$$u_0, \ u_1 ∈ \{0, \ \alpha^0 = 1, \ \alpha^1 = \alpha, \ \alpha^2\}$$

one obtains, considering the two equations $\alpha^2 = \alpha + 1$ and $\alpha^3 = \alpha^0 = 1$ again the code table of the $\text{RSC (3, 2, 2)}_4$ at symbol level.

Of course, with the same generator matrix you get exactly the same code table $\underline {u} ↔ \underline {c}$ as after the calculation via the function $u(x)$.
The corresponding code table on bit level $($see $\text{Example 2}$ on the previous page$)$ results again, if the elements are not given in exponent representation, but in coefficient form:

\[(0, \hspace{0.1cm}\alpha^{0}, \hspace{0.1cm}\alpha^{1}, \hspace{0.1cm}\alpha^{2}) \hspace{0.3cm}\Leftrightarrow\hspace{0.3cm}(00, \hspace{0.1cm}01, \hspace{0.1cm}10, \hspace{0.1cm}11) \hspace{0.05cm}. \]}}

Generator matrix and parity-check matrix

We now generalize the result of the last page for a Reed–Solomon code with

dimension $k$ $($number of symbols per information block$)$,

code word length $n$ $($number of symbols per code word$)$.

⇒ The "generator matrix" $\boldsymbol{\rm G}$ $(k$ rows, $n$ columns$)$ and the "parity-check matrix" $\boldsymbol{\rm H}$ $(n-k$ rows, $n$ columns$)$ must jointly satisfy the following equation:

$${\boldsymbol{\rm G} } \cdot { \boldsymbol{\rm H } }^{\rm T}= { \boldsymbol{\rm 0} }\hspace{0.05cm}.$$

Here, "$\boldsymbol{\rm 0}$" denotes a zero matrix $($all elements equal $0)$ with $k$ rows and $n-k$ columns.

$\text{Example 4:}$ We consider the $\text{RSC (7, 3, 5)}_8$:

code parameters $n= 7$, $k= 3$,

based on the Galois field $\rm GF(2^3 = 8)$

with the constraint $\alpha^3 =\alpha + 1$.

Note with respect to the code name:

The third parameter of the nomenclature commonly used for block codes names the free distance $d_{\rm min}= 5$.
Unlike the binary codes discussed in the chapter "Examples of binary block codes" $($single parity-check code, repetition code, Hamming code$)$, the Reed–Solomon codes still have the hint $q$ added to the Galois field $($here: $q = 8)$.

All elements of the generator matrix and the parity-check matrix,

\[{ \boldsymbol{\rm G} } = \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5} \end{pmatrix}\hspace{0.05cm},\hspace{0.4cm} { \boldsymbol{\rm H} } = \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4}\\ 1 & \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2} & \alpha^{6} & \alpha^{3} \end{pmatrix}\hspace{0.05cm}, \]

originate from the Galois field ${\rm GF}(2^3) \hspace{-0.01cm}\setminus \hspace{-0.01cm} \{0\} = \big \{\hspace{0.05cm} \alpha^{0} \hspace{0.05cm},\hspace{0.1cm}\alpha^{1}\hspace{0.05cm},\hspace{0.1cm} \alpha^{2} \hspace{0.05cm},\hspace{0.1cm} \alpha^{3} \hspace{0.05cm},\hspace{0.1cm}\alpha^{4}\hspace{0.05cm},\hspace{0.1cm} \alpha^{5} \hspace{0.05cm},\hspace{0.1cm} \alpha^{6} \hspace{0.05cm}\big \}$. For the matrix product holds:

\[{ \boldsymbol{\rm G} } \cdot { \boldsymbol{\rm H } }^{\rm T}= \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5} \end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4\\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1\\ \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5}\\ \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2}\\ \alpha^5 & \alpha^{3} & \alpha^{1} & \alpha^{6}\\ \alpha^6 & \alpha^{5} & \alpha^{4} & \alpha^{3} \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} \hspace{0.05cm}.\]

This will be demonstrated here for two elements only:

First row, first column:

\[1 \hspace{0.1cm} \cdot \hspace{0.1cm} \big [1 + \alpha^1 + \alpha^2 + \alpha^3 + \alpha^4 + \alpha^5 + \alpha^6 \big ] = 1 + \alpha + \alpha^2 + (\alpha + 1) + (\alpha^2 + \alpha)+ (\alpha^2 + \alpha +1)+ (\alpha^2 + 1) = 0 \hspace{0.05cm}; \]

Last row, last column:

\[1 \hspace{0.1cm} \cdot \hspace{0.1cm} 1 + \alpha^2 \cdot \alpha^4 + \alpha^4 \cdot \alpha^1 + \alpha^6 \cdot \alpha^5+ \alpha^1 \cdot \alpha^2+ \alpha^3 \cdot \alpha^6+ \alpha^5 \cdot \alpha^3= 1 + \alpha^6 + \alpha^5 + \alpha^{11} + \alpha^{3}+ \alpha^{9}+ \alpha^{8} =\]

\[ \hspace{1.5cm} = \hspace{0.15cm} 1 + \alpha^6 + \alpha^5 + \alpha^{4} + \alpha^{3}+ \alpha^{2}+ \alpha^{1} =0 \hspace{0.05cm}.\]

Singleton bound and minimum distance

An important parameter of any block code is the "minimum distance" between any two code words $\underline {c}_i$ and $\underline {c}_j$.

The Reed–Solomon–codes belong to the class of linear and cyclic codes. For these, one can start from the zero word $\underline {c}_0 = (0, 0, \hspace{0.05cm} \text{...} \hspace{0.05cm}, 0)$ as the reference.

From the number of zeros in the other code words $\underline {c}_j ≠ \underline {c}_0$ the "distance spectrum" $\{ \hspace{0.05cm}W_j\hspace{0.05cm}\}$ can be specified.

$\text{Example 5:}$ The table illustrates the determination of the distance spectrum for the $\text{RSC (3, 2, 2)}_4$.

Compared to the previous graphs, the symbol set is simplified by $\{0,\ 1,\ 2,\ 3\}$ instead of $\{0,\ \alpha^0,\ \alpha^1,\ \alpha^2\}$.

The distance $d$ between $\underline {c}_j$ and the null word $\underline {c}_0$ is identical to the "Hamming weight" $w_{\rm H}(\underline {c}_j)$.

To derive the distance spectrum for the $\text{RSC (3, 2, 2)}_4$

⇒ From the upper table can be read among others:

Nine code words differ from the zero word in two symbols and six code words in three symbols: $W_2 = 9$, $W_3 = 6$.
There is not a single code word with only one zero. That means: The minimum distance here is $d_{\rm min} = 2$.

⇒ From the table below one can see that also for the binary representation holds $d_{\rm min} = 2$.

This empirical result will now be generalized:

$\text{Without proof:}$

The "minimum distance" of each $(n,\ k)$ Reed–Solomon code is $d_{\rm min} =n-k+1$ ⇒ symbol errors can be detected ⇒ $e = d_{\rm min} -1 =n-k$ .
For "error correcting codes" one usually chooses $d_{\rm min} $ odd ⇒ $n-k$ even.
For Reed–Solomon codes then up to $t =(n-k)/2$ symbol errors can be corrected.
The "Singleton bound" says that $d_{\rm min} \le n-k+1$ holds for all linear codes.
Reed–Solomon codes reach this bound with equality; they are so-called "maximum distance separable codes" (short: "MDS codes").
The "distance spectrum" is composed of $W_0 = 1$ and other weight factors $W_i$ with $d ≤ i ≤ n$, where in the following equation $d_{\rm min}$ is abbreviated as $d$:

\[W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \bigg [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \bigg ]\hspace{0.05cm}.\]

Code name and code rate

The usual designation for the Reed–Solomon codes is ${\rm RSC} \ \ (n,\ k, \ d_{\rm min})_q$ with

the length $n$ of the code $($symbol number of a code word$)$,

the dimension $k$ of the code $($symbol number of an information word$)$,

the minimum distance $d_{\rm min} = n-k+1$, which is maximum corresponding to the "Singleton bound", and

the size $q = 2^m$ of the Galois field ${\rm GF}(q)$.

⇒ All elements $u_i$ of the information word $\underline{u}= (u_0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_{k-1})$ and all elements $c_i$ of the code word $\underline{c}= (c_0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, c_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, c_{n-1})$ are non-binary symbols and come from the Galois field ${\rm GF}(q)$.

⇒ For the realization these symbols are also represented in binary and one arrives at the "equivalent binary Reed–Solomon code" ${\rm RSC} \ \ (n_{\rm bin},\ k_{\rm bin}, \ d_{\rm min})_2$ with

$n_{\rm bin} = n \cdot m$ bits of a code word,

$k_{\rm bin} = k \cdot m$ bit of an information word.

⇒ The code rate is not changed by this action:

\[R_{\rm bin} = \frac{k_{\rm bin}}{n_{\rm bin}} = \frac{k \cdot m}{n \cdot m} = \frac{k}{n} = R \hspace{0.05cm}.\]

⇒ Similarly, the transition from ${\rm GF}(q)$ to ${\rm GF}(2)$ does not change the minimum distance $d_{\rm min}$.

$\text{Example 6:}$ As in $\text{Example 5}$ $($previous page$)$, we consider the $\text{RSC (3, 2, 2)}_4$.

Derivation of the distance spectra of $\text{RSC (3, 2, 2)}_4$ and $\text{RSC (6, 4, 2)}_2$

The upper table shows again the "distance spectrum" $\{ \hspace{0.05cm}W_j\hspace{0.05cm}\}$ of the $\text{RSC (3, 2, 2)}_4$.
The lower table applies to the equivalent binary Reed–Solomon code $\text{RSC (6, 4, 2)}_2$.

Note.

Both codes have the same code rate $R = k/n =2/3$.

Both codes have the same minimum distance $d_{\rm min} = 2$.

But the two codes differ in terms of the distance spectrum $\{ \hspace{0.05cm}W_j\hspace{0.05cm}\}$ and the "weight enumerator function" $W(X)$:

$$\text{RSC (3, 2, 2)}_4\text{:} \hspace{0.3cm} W_0 = 1\hspace{0.05cm}, \hspace{0.2cm}W_2 = 9\hspace{0.05cm}, \hspace{0.2cm}W_3 = 6\hspace{0.3cm}$$

$$\Rightarrow\hspace{0.3cm}W(X) = 1 + 9 \cdot X^2 + 6 \cdot X^3\hspace{0.05cm}.$$

$$\text{RSC (6, 4, 2)}_2\text{:} \hspace{0.3cm} W_0 = 1\hspace{0.05cm}, \hspace{0.2cm}W_2 = 3\hspace{0.05cm}, \hspace{0.2cm}W_3 = 8 \hspace{0.05cm}, \hspace{0.2cm}W_4 = 3\hspace{0.05cm}, \hspace{0.2cm}W_6 = 1.$$

$$\Rightarrow\hspace{0.3cm}W(X) = 1 + 3 \cdot X^2 + 8 \cdot X^3 + 4 \cdot X^4 + X^6 \hspace{0.05cm}.$$

Meaning of the Reed-Solomon codes

Using the $\text{RSC (3, 2, 2)}_4$ often considered here as an example, we were able to learn many properties of Reed–Solomon codes in a manageable way.

However, this code is not relevant in practice, since due to $d_{\rm min} = 2$ not a single error can be corrected, and not even a single error can be detected.

The next larger code $\text{RSC (7, 3, 5)}_8$, which can correct up to $t = 2$ errors, has a code table with $8^3 = 512$ entries and is unsuitable for demonstration purposes.

In practice, very large Reed–Solomon codes are usually used, for example the $\text{RSC (255, 223, 33)}_{256}$ with the following properties:

The code is based on the Galois field $\rm GF(2^8)$. Each symbol thus corresponds to one byte. The code rate is relatively large with $R = 0.8745$.
Despite this large code rate (i.e., low redundancy), this code can detect up to $e = 32$ errors within a block of $255$ symbols and can correct up to $t = 16$ errors.
The code table, however, would have $2^{8 \hspace{0.05cm}\cdot \hspace{0.05cm} 223}= 2^{ \hspace{0.05cm} 1784} ≈ 10^{537}$ entries, and is therefore unlikely to be actually created by anyone.

The great advantage of Reed–Solomon codes $($and a whole series of further codes derived from them$)$ is on the one hand that they can be constructed analytically closed, on the other hand their large flexibility regarding the code parameters. Usually one proceeds as follows:

One specifies the correction capability in the form of the parameter $t$. From this, the minimum distance $d_{\rm min} = 2t + 1$ and the difference $n-k = 2t$ corresponding to the Singleton bound. There is no better value.
Another design parameter is the code rate $R=k/n$, where the code word length $n = 2^m -1$ is not completely arbitrary. By extension, shortening and puncturing – see "Exercise 1.9Z" – the variety of possible codes can be further increased.
For Reed–Solomon codes, the weight distribution is known exactly and adaptation to the error structure of the channel is possible. These codes are particularly well suited for burst error channels, which are often present in mobile radio systems due to temporary shadowing.
In the case of statistically independent errors, "BCH codes" $($from the inventors $\rm B$ose–$\rm C$haudhuri–$\rm H$ocquenghem$)$ are more suitable. These codes are closely related to Reed–Solomon codes, but they do not always satisfy the Singleton criterion. A detailed description can be found in [Fri96]^[1].
Decoding according to the "BDD Principle" ("Bounded Distance Decoding") can be done computationally very easily, for example with the "Berlekamp–Massey Algorithm". Moreover, the decoder can also process "Soft Decision Information" without much additional effort.