Properties of Coaxial Cables

Complex propagation function of coaxial cables

Coaxial cables consist of an inner conductor and – separated by a dielectric – an outer conductor. Two different types of cable have been standardized, with the diameters of the inner and outer conductors mentioned for identification purposes:

the "standard coaxial cable" whose inner conductor has a diameter of $\text{2.6 mm}$ and whose outer diameter is $\text{9.5 mm}$,
the "small coaxial cable" with dimensions $\text{1.2 mm}$ and $\text{4.4 mm}$.

The cable frequency response $H_{\rm K}(f)$ results from the cable length $l$ and the complex propagation function (per unit length)

$$\gamma(f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot (\beta_1 \cdot f + \beta_2 \cdot \sqrt {f})\hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{-\gamma(f)\hspace{0.05cm} \cdot \hspace{0.05cm} l} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = {\rm e}^{-\alpha(f)\hspace{0.05cm} \cdot \hspace{0.05cm} l}\hspace{0.05cm}.$$

The cable specific constants for the »standard coaxial cable« $\text{(2.6/9.5 mm)}$ are:

$$\begin{align*}\alpha_0 & = 0.00162\, \frac{ {\rm Np} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.000435\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.2722\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}, \\ \beta_1 & = 21.78\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.2722\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.\end{align*}$$

Accordingly, the kilometric attenuation and phase constants for the »small coaxial cable« $\text{(1.2/4.4 mm)}$:

$$\begin{align*}\alpha_0 & = 0.00783\, \frac{ {\rm Np} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.000443\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.5984\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}, \\ \beta_1 & = 22.18\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.5984\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.\end{align*}$$

These values can be calculated from the geometric dimensions of the cables and have been confirmed by measurements at the Fernmeldetechnisches Zentralamt in Darmstadt - see [Wel77]^[1]. They apply to a temperature of $20^\circ\ \text{C (293 K)}$ and frequencies greater than $\text{200 kHz}$.

There is the following connection to the $\text{primary line parameters}$:

The ohmic losses originating from the frequency-independent component $R\hspace{0.05cm}'$ are modeled by the parameter $α_0$ and cause a (small for coaxial cables) frequency-independent attenuation.
The component $α_1 · f$ of the attenuation function (per unit length) is due to the derivation losses $(G\hspace{0.08cm}’)$ and the frequency-proportional term $β_1 · f$ causes only delay but no distortion.
The components $α_2$ and $β_2$ are due to the $\text{skin effect}$, which causes the current density inside the conductor to be lower than at the surface in the case of higher-frequency alternating current. As a result, the serial resistance (per unit length) $R\hspace{0.05cm}’$ of an electric line increases with the square root of the frequency.

Characteristic cable attenuation

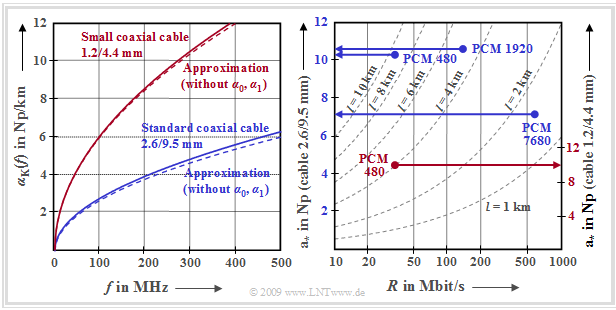
The graph shows the frequency-dependent attenuation curve for the normal coaxial cable and the small coaxial cable. Shown on the left is the cable attenuation per unit length of the two coaxial cable types in the frequency range up to $\text{500 MHz}$:

Attenuation function and characteristic attenuation of coaxial cables

$${\alpha}_{\rm K}(f) \hspace{-0.05cm} = \alpha_0 \hspace{-0.05cm}+ \hspace{-0.05cm} \alpha_1 \cdot f \hspace{-0.05cm}+ \hspace{-0.05cm} \alpha_2 \hspace{-0.05cm}\cdot \hspace{-0.05cm}\sqrt {f} \hspace{0.01cm} \hspace{0.01cm}.$$

$$\Rightarrow \hspace{0.3cm}{\rm a}_{\rm K}(f) =\alpha_{\rm K}(f) \cdot l $$

Notes on the representation chosen here

To make the difference between the attenuation function per unit length "alpha" and the function "a" (after multiplication by length) more recognizable, the attenuation function is written here as ${\rm a}_{\rm K}(f)$ and not (italics) as ${a}_{\rm K}(f)$.
The ordinate labeling is given here in "Np/km" Often it is also done in "dB/km", with the following conversion:

$$\ln(10)/20 = 0.11513\text{...} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 1 \ \rm dB = 0.11513\text{... Np.} $$

Interpretation of the left graph

It can be seen from the curves shown that the error is still tolerable when neglecting the frequency-independent component $α_0$ and the frequency-proportional term $(α_1\cdot f)$.
In the following, we therefore assume the following simplified attenuation function:

$${\rm a}_{\rm K}(f) = \alpha_2 \cdot \sqrt {f} \cdot l = {\rm a}_{\rm \star}\cdot \sqrt { {2f}/{R}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = {\rm e}^{- {\rm a}_{\rm K}(f)}\hspace{0.05cm}, \hspace{0.2cm} {\rm a}_{\rm K}(f)\hspace{0.15cm}{\rm in }\hspace{0.15cm}{\rm Np}\hspace{0.05cm}.$$

$\text{Definition:}$ As »characteristic cable attenuation« $\rm a_∗$ we denote the attenuation of a coaxial cable at half the bit rate due to the $α_2$ term alone ⇒ "skin effect", thus neglecting the $α_0$ and the $α_1$ term:

$${\rm a}_{\rm \star} = {\rm a}_{\rm K}(f = {R}/{2}) = \alpha_2 \cdot \sqrt {{R}/{2}} \cdot l\hspace{0.05cm}.$$

This value is particularly suitable for comparing different conducted transmission systems with different

coaxial cable types (for example, normal or small coaxial cable), each identified by the parameter $\alpha_2$,
bit rates $(R)$, and
cable lengths $(l)$.

Interpretation of the right graph

The right diagram shows the characteristic cable attenuation $\rm a_∗$ in "Neper" (Np) as a function of the bit rate $R$ and the cable length $l$

for the normal coaxial cable ("2.6/9.5 mm", left ordinate labeling) and
for the small coaxial cable ("1.2/4.4 mm", right ordinate labeling).

This diagram shows the PCM systems of hierarchy levels $3$ to $5$ proposed by the $\text{ITU-T}$ ("ITU Telecommunication Standardization Sector") in the 1970s. One recognizes:

For all these systems for PCM speech transmission, the characteristic cable attenuation assumes values between $7 \ \rm Np \ \ (≈ 61 \ dB)$ and $10.6 \ \rm Np \ \ (≈ 92 \ dB)$ .
The system $\text{PCM 480}$ – designed for 480 simultaneous telephone calls - with the bit rate $R ≈ 35 \ \rm Mbit/s$ was specified for both the normal coaxial cable $($with $l = 9.3 \ \rm km)$ and for the small coaxial cable $($with $l = 4 \ \rm km)$. The $\rm a_∗$values $10.4\ \rm Np$ and $9.9\ \rm Np$ respectively are in the same order of magnitude.
The transmission system $\text{PCM 1920}$ of the fourth hierarchy level (specified for the normal coaxial cable) with $R ≈ 140 \ \rm Mbit/s$ and $l = 4.65 \ \rm km$ is parameterized by $\rm a_∗ = 10.6 \ \rm Np$ or $10.6 \ {\rm Np}· 8.688 \ \rm dB/Np ≈ 92\ \rm dB$ .
Although the system $\text{PCM 7680}$ in contrast has four times the capacity $R ≈ 560 \rm Mbit/s$ , the characteristic cable attenuation of $\rm a_∗ ≈ 61 \ dB$ is due to the better medium "normal coaxial cable" and the shorter cable sections by a factor of $3$ $(l = 1. 55 \ \rm km)$ significantly lower.
These numerical values also show that for coaxial cable systems, the cable length $l$ is more critical than the bit rate $R$. If one wants to double the cable length, one has to reduce the bit rate by a factor $4$ .

You can view the topic described here with the interactive HTLM 5/JS applet "Attenuation of Copper Cables" .

Impulse response of a coaxial cable

To calculate the impulse response, the first two components of the five attenuation components of the complex propagation function (per unit length) can be neglected (the reasoning can be found in the previous section). So we start from the following equation:

$$\gamma(f) = \alpha_0 + \alpha_1 \cdot f + {\rm j} \cdot \beta_1 \cdot f +\alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot \beta_2 \cdot \sqrt {f} \approx {\rm j} \cdot \beta_1 \cdot f +\alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot \beta_2 \cdot \sqrt {f} \hspace{0.05cm}.$$

Considering

the cable length $l$,
the characteristic cable attenuation $\rm a_∗$ and
that $α_2$ (in "Np") and $β_2$ (in "rad") are numerically equal,

thus applies to the frequency response of the coaxial cable:

$$H_{\rm K}(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f} \cdot {\rm e}^{-{\rm a}_{\rm \star}\hspace{0.05cm}\cdot \hspace{0.05cm} \sqrt{2f/R} }\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}{\rm a}_{\rm \star}\hspace{0.05cm}\cdot \hspace{0.02cm} \sqrt{2f/R}}= {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f} \cdot {\rm e}^{-2{\rm a}_{\rm \star}\hspace{0.03cm}\cdot \hspace{0.03cm} \sqrt{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}f/R}} \hspace{0.05cm}.$$

The following abbreviations are used here:

$$b_1\hspace{0.1cm}{(\rm in }\hspace{0.15cm}{\rm rad)}= \beta_1 \cdot l \hspace{0.05cm}, \hspace{0.8cm} {\rm a}_{\rm \star}\hspace{0.1cm}{(\rm in }\hspace{0.15cm}{\rm Np)}= \alpha_2 \cdot \sqrt {R/2} \cdot l \hspace{0.05cm}.$$

The time domain display is obtained by applying the $\text{Fourier inverse transform}$ and the $\text{Convolution theorem}$:

$$h_{\rm K}(t) = \mathcal{F}^{-1} \left \{ {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f}\right \} \star\mathcal{F}^{-1} \left \{ {\rm e}^{-2{\rm a}_{\rm \star}\hspace{0.03cm}\cdot \hspace{0.03cm} \sqrt{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}f/R} }\right \} \hspace{0.05cm}.$$

To be considered here:

The first term yields the Dirac delta function $δ(t - τ_{\rm P})$ shifted by the phase delay $τ_{\rm P} = b_1/2π$ .
The second term can be given analytically closed. We write $h_{\rm K}(t + τ_P)$, so that the phase delay $τ_{\rm P}$ need not be considered further.

$$h_{\rm K}(t + \tau_{\rm P}) = \frac {{\rm a}_{\rm \star}}{\pi \cdot \sqrt{2 \cdot R \cdot t^3}}\cdot {\rm exp} \left [ -\frac {{\rm a}_{\rm \star}^2}{ {2\pi \cdot R\cdot t}} \right ]\hspace{0.05cm},\hspace{0.2cm}{\rm a}_{\rm \star}\hspace{0.15cm}{\rm in\hspace{0.15cm} Np}\hspace{0.05cm}.$$

Since the bit rate $R$ also has already been considered in the definition of the characteristic cable attenuation $\rm a_∗$ this equation can be easily represented with the normalized time $t\hspace{0.05cm}' = t/T$ :

$$h_{\rm K}(t\hspace{0.05cm}' + \tau_{\rm P}\hspace{0.05cm} ') = \frac {1}{T} \cdot \frac {{\rm a}_{\rm \star}}{\pi \cdot \sqrt{2 \cdot t\hspace{0.05cm}'\hspace{0.05cm}^3}}\cdot {\rm exp} \left [ -\frac {{\rm a}_{\rm \star}^2}{ {2\pi \cdot t\hspace{0.05cm}'}} \right ]\hspace{0.05cm},\hspace{0.2cm}{\rm a}_{\rm \star}\hspace{0.15cm}{\rm in\hspace{0.15cm} Np}\hspace{0.05cm}.$$

Here $T = 1/R$ denotes the symbol duration of a binary system and it holds $τ_{\rm P} \hspace{0.05cm}' = τ_{\rm P}/T$.

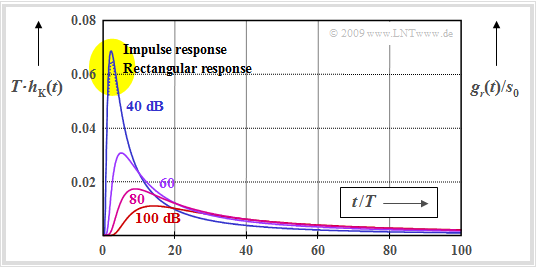
$\text{Example 1:}$ The results of this section are illustrated by the following graph as an example.

Impulse response of a coaxial cable with $\rm a_∗ = 60 \ dB$

The normalized impulse response $T · h_{\rm K}(t)$ of a coaxial cable with $\rm a_∗ = 60 \ dB \ \ (6.9\ Np)$ is shown.
The attenuation coefficients $α_0$ and $α_1$ can thus be neglected, as shown in the last section.
For the left graph, the parameter $β_1 = 0$ was also set.

Because of the parameterization by the coefficient $a_∗$ suitable for this purpose and the normalization of the time to the symbol duration $T$ the left curve is equally valid for systems with small or normal coaxial cable, different lengths and different bit rates, for example for a

normal coaxial cable $\text{2.6/9.5 mm}$, bit rate $R = 140 \ \rm Mbit/s$, cable length $l = 3 \ \rm km$ ⇒ system $\rm A$,
small coaxial cable $\text{1.2/4.4 mm mm}$, bit rate $R = 35 \ \rm Mbit/s$, cable length $l = 2.8 \ \rm km$ ⇒ system $\rm B$.

It can be seen that even at this moderate cable attenuation $\rm a_∗ = 60 \ \rm dB$ the impulse response already extends over more than $200$ symbol durations due to the skin effect $(α_2 = β_2 ≠ 0)$. Since the integral over $h_{\rm K}(t)$ is equal to $H_{\rm K}(f = 0) = 1$, the maximum value becomes very small:

$${\rm Max}\big [h_{\rm K}(t)\big ] \approx 0.03.$$

In the diagram on the right, the effects of the phase parameter $β_1$ can be seen. Note the different time scales of the left and the right diagram:

For system $\rm A$ $(β_1 = 21.78 \ \rm rad/(km · MHz)$, $T = 7.14\ \rm ns)$ $β_1$ leads to a phase delay of

$$\tau_{\rm A}= \frac {\beta_1 \cdot l}{2\pi} =\frac {21.78\, { {\rm rad} }/{ {(\rm km \cdot MHz)} }\cdot 3\,{\rm km} }{2\pi} = 10.4\,{\rm \mu s}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\tau_{\rm A}\hspace{0.05cm}' = {\tau_{\rm A} }/{T} \approx 1457\hspace{0.05cm}.$$

On the other hand, the following can be obtained for system $\rm B$ $(β_1 = 22.18 \ \rm rad/(km · MHz)$, $T = 30 \ \rm ns)$:

$$\tau_{\rm B}= \frac {\beta_1 \cdot l}{2\pi} =\frac {22.18\, { {\rm rad} }/{ {(\rm km \cdot MHz)} }\cdot 2.8\,{\rm km} }{2\pi} = 9.9\,{\rm µ s}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\tau_{\rm B}\hspace{0.05cm}' ={\tau_{\rm B} }/{T} \approx 330\hspace{0.05cm}.$$

Although $τ_{\rm A} ≈ τ_{\rm B}$ holds, completely different ratios result because of the time normalization to $T = 1/R$ .

$\text{Conclusion:}$ When simulating and optimizing communication systems,

one usually omits the phase term with $b_1 = β_1 · l$,
since this results exclusively in a (often not disturbing) phase delay, but no signal distortion.

Basic receiver pulse

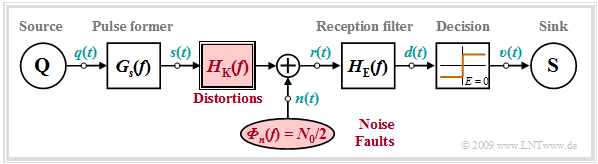
With the basic transmission pulse $g_s(t)$ ⇒ "basic pulse of the transmitted signal $s(t)$" and the impulse response $h_{\rm K}(t)$ of the channel, the result for the basic receiver pulse $g_r(t)$ ⇒ "basic pulse of the received signal $r(t)$" is:

$$g_r(t) = g_s(t) \star h_{\rm K}(t)\hspace{0.05cm}.$$

If a non-return-to-zero (NRZ) rectangular pulse $g_s(t)$ with amplitude $s_0$ and duration $Δt_s = T$ is used at the transmitter, the following results for the basic pulse at the receiver input:

$$g_r(t) = 2 s_0 \cdot \left [ {\rm Q} \left (\frac {{\rm a}_{\rm \star}/\sqrt {\pi}}{ \sqrt{ (t/T - 0.5)}}\right ) - {\rm Q} \left (\frac {{\rm a}_{\rm \star}/\sqrt {\pi}}{ \sqrt{ (t/T + 0.5)}}\right ) \right ]\hspace{0.05cm}.$$

Here $\rm a_∗$ denotes the characteristic cable attenuation (in Neper) and ${\rm Q}(x)$ the $\text{complementary Gaussian error function}$.

Impulse response of the coaxial cable and basic receiver pulse

$\text{Example 2:}$ The figure shows for the characteristic cable attenuations $\rm a_∗ = 40 \ \rm dB$, ... , $100 \ \rm dB$ (smaller $\rm a_∗$–values are not relevant for practice)

the normalized coaxial cable impulse response $T · h_{\rm K}(t)$ ⇒ solid curves,
the basic receiver pulse ("rectangular response") $g_r(t)$ normalized to the transmission amplitude $s_0$ ⇒ dotted line.

One recognizes the following from this diagram:

With $\rm a_∗ = 40 \ \rm dB$, the normalized rectangular response $g_r(t)/s_0$ is slightly (about a factor of $0.95)$ smaller at the peak than the normalized impulse response $T · h_{\rm K}(t)$. Here is a small difference between impulse response and basic receiver pulse .
In contrast, for the case $a_∗ ≥ 60 \ \rm dB$, the rectangular response and the impulse response are indistinguishable within the drawing accuracy.
For a return-to-zero (RZ) pulse, the above equation for the basic receiver pulse would still need to be multiplied by the duty cycle $Δt_s/T$ . In this case $g_r(t)/s_0$ is smaller than $T · h_{\rm K}(t)$ by at least this factor.
The equation modified in this way is also a good approximation for other basic transmission pulses as long as $\rm a_∗≥ 60 \ \rm dB$ is sufficiently large. $Δt_s$ then indicates the $\text{equivalent pulse duration}$ of $g_r(t)$.

We draw your attention to the (German language) interactive SWF applet "Zeitverhalten von Kupferkabeln" ⇒ "Time behavior of copper cables", which deals with the topic discussed here.

Special features of coaxial cable systems

Assuming binary transmission with non-return-to-zero (NRZ) rectangular pulses $($symbol duration $T)$ and a coaxial transmission channel, the following system model is obtained. In particular, it should be noted:

Binary transmission system with coaxial cable KORREKTUR: receiver filter, noise faults

In a simulation, the phase delay time of the coaxial cable is conveniently left out of consideration. Then the basic receiver pulse $g_r(t)$ (with ${\rm a}_{\rm \star}$ in Neper) is approximated by

$$g_r(t) \approx s_0 \cdot T \cdot h_{\rm K}(t) = \frac {s_0 \cdot {\rm a}_{\rm \star}/\pi}{ \sqrt{2 \cdot(t/T)^3}}\cdot {\rm e}^{ -{{\rm a}_{\rm \star}^2}/( {2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}t/T}) } \hspace{0.05cm}.$$

Because of the good shielding of coaxial cables against other impairments, the $\text{thermal noise}$ is the dominant stochastic perturbation. In this case, the signal $n(t)$ is Gaussian and white. It can described by the (two-sided) noise power density $N_0/2$.
By far the largest noise component arises in the input stage of the receiver, so that it is expedient to add the noise signal $n(t)$ at the interface "cable ⇒ receiver".
This noise addition point is also useful because the frequency response $H_{\rm K}(f)$ decisively attenuates all noise accumulated along the cable.
Then the received signal is with the amplitude coefficients $a_{\nu}$:

$$r(t) = \sum_{\nu = - \infty}^{+ \infty}a_{\nu}\cdot g_r(t - \nu \cdot T)+ n(t) \hspace{0.05cm} .$$

Exercises for the chapter

Exercise 4.4: Coaxial Cable - Frequency Response

Exercise 4.5: Coaxial Cable - Impulse Response

Exercise 4.5Z: Impulse Response once again

References

↑ Wellhausen, H. W.: Dämpfung, Phase und Laufzeiten bei Weitverkehrs–Koaxialpaaren. Frequenz 31, S. 23-28, 1977.

[1] Wellhausen, H. W.: Dämpfung, Phase und Laufzeiten bei Weitverkehrs–Koaxialpaaren. Frequenz 31, S. 23-28, 1977.

[1]