Different Entropy Measures of Two-Dimensional Random Variables
Contents
Definition der Entropie unter Verwendung von supp(PXY)
Wir fassen die Ergebnisse des letzten Abschnitts nochmals kurz zusammen, wobei wir von der zweidimensionalen Zufallsgröße $XY$ mit der Wahrscheinlichkeitsfunktion $P_{XY}(X, Y)$ ausgehen. Gleichzeitig verwenden wir die Schreibweise
$${\rm supp} (P_{XY}) = \big \{ \hspace{0.05cm}(x, y) \in XY \hspace{0.05cm}, \hspace{0.3cm} {\rm wobei} \hspace{0.15cm} P_{XY}(X, Y) \ne 0 \hspace{0.05cm} \big \} \hspace{0.05cm}.$$
Mit dieser Teilmenge $\text{supp}(P_{XY}) ⊂ P_{XY}$ gilt für
- die Verbundentropie (englisch: Joint Entropy):
$$H(XY) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] =\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.05cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{XY}(x, y)} \hspace{0.05cm}.$$
- die Entropien der 1D–Zufallsgrößen $X$ und $Y$:
$$H(X) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(X)}\right ] =\hspace{-0.2cm} \sum_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{X})} \hspace{-0.2cm} P_{X}(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(x)} \hspace{0.05cm},$$
$$H(Y) = {\rm E}\hspace{-0.1cm} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{Y}(Y)}\right ] =\hspace{-0.2cm} \sum_{y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{Y})} \hspace{-0.2cm} P_{Y}(y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{Y}(y)} \hspace{0.05cm}.$$
Bei der zweidimensionalen (2D) Wahrscheinlichkeitsfunktion PRS(R, S) unseres Würfel–Experimentes mit
- $R$: Augenzahl des roten Würfels,
- $S$: Summe der beiden Würfel $R$ und $B$
gibt es 6 · 11 = 66 Felder, von denen viele leer sind ⇒ Wahrscheinlichkeit 0. Die Teilmenge $\text{supp}(P_{RS})$ beinhaltet dagegen nur die 36 schraffierten Felder mit von 0 verschiedenen Wahrscheinlichkeiten. Die Entropie bleibt gleich, ganz egal, ob man die Mittelung über alle Elemente von $P_{RS}$ oder nur über die Elemente von $\text{supp}(P_{RS})$ erstreckt, da $x · \log_2 (\frac{1}{x})$ für $x$ → 0 gleich 0 ergibt. Dagegen sind bei der 2D–Wahrscheinlichkeitsfunktion $P_{RB}(R, B)$ mit
- $R$: Augenzahl des roten Würels,
- $B$: Augenzahl des blauen Würfels
die Mengen $P_{RB}$ und $\text{supp}(P_{RB})$ identisch. Hier sind alle $6^2 = 36$ Felder mit Werten ≠ 0 belegt.
Bedingte Wahrscheinlichkeit und bedingte Entropie
Im Buch Stochastische Signaltheorie wurden für den Fall zweier Ereignisse $X$ und $Y$ die folgenden bedingten Wahrscheinlichkeiten angegeben ⇒ Satz von Bayes:
$${\rm Pr} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = \frac{{\rm Pr} (X \cap Y)}{{\rm Pr} (Y)} \hspace{0.05cm}, \hspace{0.5cm} {\rm Pr} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = \frac{{\rm Pr} (X \cap Y)}{{\rm Pr} (X)} \hspace{0.05cm}.$$
Angewendet auf Wahrscheinlichkeitsfunktionen erhält man somit:
$$P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = \frac{P_{XY}(X, Y)}{P_{Y}(Y)} \hspace{0.05cm}, \hspace{0.5cm} P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = \frac{P_{XY}(X, Y)}{P_{X}(X)} \hspace{0.05cm}.$$
Analog zur Verbundentropie $H(XY)$ lassen sich hier folgende Entropiefunktionen ableiten:
Die bedingte Entropie (englisch: Conditional Entropy) der Zufallsgröße $X$ lautet unter der Bedingung $Y$:
$$\begin{align*}H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ] \hspace{-0.15cm}&=\hspace{-0.15cm}\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)}=\\ &=\hspace{-0.15cm}\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{Y}(y)}{P_{XY}(x, y)} \hspace{0.05cm}.\end{align*}$$
In gleicher Weise erhält man für die zweite bedingte Entropie:
$$\begin{align*}H(Y \hspace{-0.1cm}\mid \hspace{-0.05cm} X) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}Y\hspace{0.03cm} \mid \hspace{0.01cm} X} (Y \hspace{-0.08cm}\mid \hspace{-0.05cm}X)}\right ] \hspace{-0.15cm}&=\hspace{-0.15cm}\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y\hspace{-0.03cm} \mid \hspace{-0.01cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)}=\\ &=\hspace{-0.15cm}\hspace{-0.2cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{X}(x)}{P_{XY}(x, y)} \hspace{0.05cm}.\end{align*}$$
Im Argument der Logarithmusfunktion steht stets eine bedingte Wahrscheinlichkeitsfunktion ⇒ $P_{X|Y}(·)$ bzw. $P_{Y|X}(·)$, während zur Erwartungswertbildung die Verbundwahrscheinlichkeit $P_{XY}(·)$ benötigt wird.
Für die bedingten Entropien gibt es folgende Begrenzungen:
- Sowohl $H(X|Y)$ als auch $H(Y|X)$ sind stets größer oder gleich 0. Aus $H(X|Y)$ = 0 folgt direkt auch $H(Y|X)$ = 0. Beides ist nur für disjunkte Mengen $X$ und $Y$ möglich.
- Es gilt stets $H(X|Y) ≤ H(X)$ sowie $H(Y|X) ≤ H(Y)$. Diese Aussage ist einleuchtend, wenn man sich bewusst macht, dass man für Entropie synonym auch Unsicherheit verwenden kann.
- Denn: Die Unsicherheit bezüglich $X$ kann nicht dadurch größer werden, dass man $Y$ kennt. Außer bei statistischer Unabhängigkeit ⇒ $H(X|Y)$ = $H(X)$ gilt stets $H(X|Y) < H(X)$.
- Wegen $H(X) ≤ H(XY)$, $H(Y) ≤ H(XY)$ gilt somit auch $H(X|Y) ≤ H(XY)$ und $H(Y|X) ≤ H(XY)$. Eine bedingte Entropie kann also nie größer werden als die Verbundentropie.
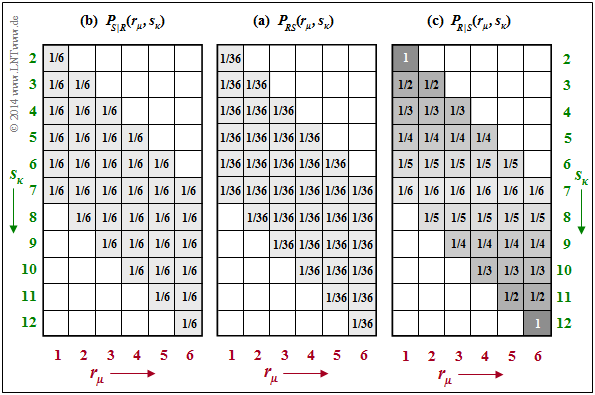
Beispiel F: Wir betrachten die Verbundwahrscheinlichkeiten $P_{RS}(·)$ unseres Würfelexperiments, die im Beispiel D ermittelt wurden. In der Mitte der folgenden Grafik ist $P_{RS}(·)$ nochmals angegeben.
Außen sind die beiden bedingten Wahrscheinlichkeitsfunktionen gezeichnet:
- Links dargestellt ist die bedingte Wahrscheinlichkeitsfunktion $P_{S|R}(⋅)$ = $P_{SR}(⋅)/P_R(⋅)$. Wegen $P_R(R)$ = [1/6, 1/6, 1/6, 1/6, 1/6, 1/6] steht hier in allen schraffierten Feldern ⇒ $\text{supp}(P_{S|R})$ = $\text{supp}(P_{R|S})$ der gleiche Wahrscheinlichkeitswert 1/6. Daraus folgt für die bedingte Entropie:
$$H(S \hspace{-0.1cm}\mid \hspace{-0.13cm} R) = \hspace{-0.2cm} \sum_{(r, s) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{RS})} \hspace{-0.6cm} P_{RS}(r, s) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}S \hspace{0.03cm} \mid \hspace{0.03cm} R} (s \hspace{-0.05cm}\mid \hspace{-0.05cm} r)} = 36 \cdot \frac{1}{36} \cdot {\rm log}_2 \hspace{0.1cm} (6) = 2.585\,{\rm bit} \hspace{0.05cm}.$$
- Für die andere bedingte Wahrscheinlichkeitsfunktion $P_{R|S}(⋅)$ = $P_{RS}(⋅)/P_S(⋅)$ mit $P_S(⋅)$ gemäß Beispiel D ergeben sich die gleichen Felder ungleich 0 ⇒ $\text{supp}(P_{R|S})$ = $\text{supp}(P_{S|R})$. Die Wahrscheinlichkeitswerte nehmen nun aber von der Mitte (1/6) zu den Rändern hin bis zur Wahrscheinlichkeit 1 in den Ecken kontinuierlich zu. Daraus folgt:
$$H(R \hspace{-0.1cm}\mid \hspace{-0.13cm} S) = \frac{1}{36} \cdot {\rm log}_2 \hspace{0.1cm} (6) + \frac{2}{36} \cdot \sum_{i=1}^5 \left [ i \cdot {\rm log}_2 \hspace{0.1cm} (i) \right ]= 1.896\,{\rm bit} \hspace{0.05cm}.$$
Dagegen ergibt sich für die Zufallsgröße $RB$ gemäß Beispiel C wegen $P_{RB}(⋅)$ = $P_R(⋅) · P_B(⋅)$:
$$\begin{align*}H(B \hspace{-0.1cm}\mid \hspace{-0.13cm} R) \hspace{-0.15cm} & = \hspace{-0.15cm} H(B) = {\rm log}_2 \hspace{0.1cm} (6) = 2.585\,{\rm bit} \hspace{0.05cm},\\ H(R \hspace{-0.1cm}\mid \hspace{-0.13cm} B) \hspace{-0.15cm} & = \hspace{-0.15cm} H(R) = {\rm log}_2 \hspace{0.1cm} (6) = 2.585\,{\rm bit} \hspace{0.05cm}.\end{align*}$$
Transinformation zwischen zwei Zufallsgrößen
Wir betrachten die Zufallsgröße $XY$ mit der 2D–Wahrscheinlichkeitsfunktion $P_{XY}(X, Y)$. Bekannt seien auch die 1D–Funktionen $P_X(X)$ und $P_Y(Y)$. Nun stellen sich folgende Fragen:
- Wie vermindert die Kenntnis der Zufallsgröße $Y$ die Unsicherheit bezüglich $X$?
- Wie vermindert die Kenntnis der Zufallsgröße $X$ die Unsicherheit bezüglich $Y$?
Zur Beantwortung benötigen wir eine für die Informationstheorie substantielle Definition:
Die Transinformation (englisch: Mutual Information) zwischen den Zufallsgrößen $X$ und $Y$ – beide über dem gleichen Alphabet – ist gegeben durch den Ausdruck
$$I(X;Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(X, Y)} {P_{X}(X) \cdot P_{Y}(Y) }\right ] =\hspace{-0.25cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{XY})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(x, y)} {P_{X}(x) \cdot P_{Y}(y) } \hspace{0.01cm}.$$
Ein Vergleich mit Kapitel 3.1 zeigt, dass die Transinformation auch als Kullback–Leibler–Distanz zwischen der 2D–PMF $P_{XY}(⋅)$ und dem Produkt $P_X(⋅) · P_Y(⋅)$ geschrieben werden kann:
$$I(X;Y) = D(P_{XY} \hspace{0.05cm}|| \hspace{0.05cm} P_X \cdot P_Y) \hspace{0.05cm}.$$
Es ist offensichtlich, dass stets $I(X; Y)$ ≥ 0 gilt. Wegen der Symmetrie ist auch $I(Y; X)$ = $I(X; Y)$.
Sucht man in einem Wörterbuch die Übersetzung für „mutual”, so findet man unter Anderem die Begriffe „gemeinsam”, „gegenseitig”, „beidseitig” und „wechselseitig”. Und ebenso sind in Fachbüchern für $I(X; Y)$ auch die Bezeichnungen gemeinsame Entropie und gegenseitige Entropie üblich. Wir sprechen aber im Folgenden durchgängig von der Transinformation $I(X; Y)$ und interpretieren nun diese Größe:
- Durch Aufspalten des log2–Arguments entsprechend
$$I(X;Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm} \frac{1} {P_{X}(X) }\right ] - {\rm E} \hspace{-0.1cm}\left [ {\rm log}_2 \hspace{0.1cm} \frac {P_{Y}(Y) }{P_{XY}(X, Y)} \right ] $$
erhält man unter Verwendung von $P_{X|Y}(⋅)$ = $P_{XY}(⋅)/_PY(Y)$:
$$I(X;Y) = H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) \hspace{0.05cm}.$$
Das heißt: Die Unsicherheit hinsichtlich der Zufallsgröße $X$ ⇒ Entropie $H(X)$ vermindert sich bei Kenntnis von $Y$ um den Betrag $H(X|Y)$. Der Rest ist die Transinformation $I(X; Y)$.
- Bei anderer Aufspaltung kommt man zum Ergebnis:
$$I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) \hspace{0.05cm}.$$
Ergo: Die Transinformation $I(X; Y)$ ist symmetrisch: $X$ sagt genau so viel über $Y$ aus wie $Y$ über $X$ ⇒ gegenseitige Information. Das Semikolon weist auf die Gleichberechtigung hin.
Oft werden die hier genannten Gleichungen durch ein Schaubild verdeutlicht, so auch in den folgenden Beispielen. Daraus erkennt man, dass auch folgende Gleichungen zutreffen:
$$\begin{align*}I(X;Y) \hspace{-0.15cm} & = \hspace{-0.15cm} H(X) + H(Y) - H(XY) \hspace{0.05cm},\\ I(X;Y) \hspace{-0.15cm} & = \hspace{-0.15cm} H(XY) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) \hspace{0.05cm}.\end{align*}$$
Beispiel F: Wir kommen nochmals auf das Würfel–Experiment mit dem roten $(R)$ und dem blauen $(B)$ Würfel zurück. Die Zufallsgröße $S$ gibt die Summe der beiden Würfel an: $S = R + B$. Wir betrachten hier die 2D–Zufallsgröße RS. In früheren Beispielen haben wir berechnet:
- die Entropien $H(R)$ = 2.585 bit und $H(S)$ = 3.274 bit ⇒ Beispiel D,
- die Verbundentropie $H(RS)$ = 5.170 bit ⇒ Beispiel D,
- die bedingten Entropien $H(S|R)$ = 2.585 bit und $H(R|S)$ = 1.896 bit ⇒ Beispiel F.
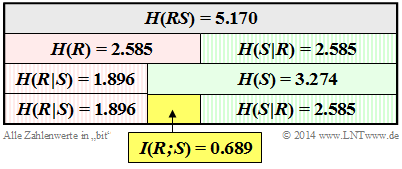
Diese Größen sind in der Grafik zusammengestellt, wobei die Zufallsgröße $R$ durch die Grundfarbe „Rot” und die Summe $S$ durch die Grundfarbe „grün” markiert sind. Bedingte Entropien sind schraffiert. Man erkennt aus dieser Darstellung:
- Hier ist $H(R)$ = $\log_2 $(6) = 2.585 bit genau halb so groß wie die Verbundentropie $H(RS)$. Kennt man $R$, so liefert $S$ genau die gleiche Information wie die Zufallsgröße $B$, nämlich $H(S|R)$ = $H(B)$ = $\log_2(6)$ = 2.585 bit. Hinweis: $H(R)$ = $H(S|R)$ gilt nicht allgemein.
- Die Entropie $H(S)$ = 3.274 bit ist im vorliegenden Beispiel erwartungsgemäß größer als $H(R)$. Wegen $H(S) + H(R|S) = H(R) + H(S|R)$ muss deshalb $H(R|S)$ gegenüber $H(S|R)$ um den gleichen Betrag $I(R; S)$ = 0.689 bit kleiner sein wie $H(R)$ gegenüber $H(S)$.
- Die Transinformation (englisch: Mutual Information) zwischen den Zufallsgrößen $R$ und $S$ ergibt sich aber auch aus der Gleichung
$$\begin{align*}I(R;S) \hspace{-0.15cm} & = \hspace{-0.15cm} H(R) + H(S) - H(RS) =\\ & = \hspace{-0.15cm} 2.585\,{\rm bit} + 3.274\,{\rm bit} - 5.170\,{\rm bit} = 0.689\,{\rm bit} \hspace{0.05cm}. \end{align*}$$
Bedingte Transinformation
Wir betrachten nun drei Zufallsgrößen $X$, $Y$ und $Z$, die zueinander in Beziehung stehen (können).
Die bedingte Transinformation (englisch: Conditional Mutual Information) zwischen den Zufallsgrößen $X$ und $Y$ bei gegebenem Z = z lautet:
$$I(X;Y \hspace{0.05cm}|\hspace{0.05cm} Z = z) = H(X\hspace{0.05cm}|\hspace{0.05cm} Z = z) - H(X|\hspace{0.05cm}Y ,\hspace{0.05cm} Z = z) \hspace{0.05cm}.$$
Dagegen bezeichnet man als die bedingte Transinformation zwischen den Zufallsgrößen $X$ und $Y$ bei gegebener Zufallsgröße Z:
$$I(X;Y \hspace{0.05cm}|\hspace{0.05cm} Z ) = H(X\hspace{0.05cm}|\hspace{0.05cm} Z ) - H(X|\hspace{0.05cm}Y Z )= \hspace{-0.3cm} \sum_{z \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (P_{Z})} \hspace{-0.25cm} P_{Z}(z) \cdot I(X;Y \hspace{0.05cm}|\hspace{0.05cm} Z = z) \hspace{0.05cm}.$$
Hierbei ist $P_Z(Z)$ die Wahrscheinlichkeitsfunktion der neben $X$ und $Y$ betrachteten Zufallsgröße $Z$ und $P_Z(z)$ die Wahrscheinlichkeit für $Z = z$.
Bitte beachten Sie: Für die bedingte Entropie gilt bekanntlich die Größenrelation $H(X|Z) ≤ H(X)$. Für die Transinformation gilt diese Größenrelation nicht unbedingt:
- $I(X; Y|Z)$ kann kleiner, gleich, aber auch größer sein als $I(X; Y)$.
Wir betrachten die binären Zufallsgrößen $X$, $Y$ und $Z$ mit folgenden Eigenschaften:
- $X$ und $Y$ seien statistisch unabhängig und für ihre Wahrscheinlichkeitsfunktionen gelte: $P_X(X)$ = [1/2, 1/2], $P_Y(Y)$ = [1– $p$, $p$] ⇒ $H(X)$ = 1 (bit), $H(Y)$ = $H_{\text{bin}}(p)$.
- $Z$ ist die Modulo–2–Summe von $X$ und $Y$: $Z = X ⊕ Y$.
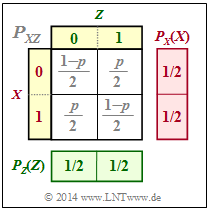
Aus der Verbund–PMF $P_{XZ}$ gemäß der oberen Grafik folgt:
- Durch Summation der Spalten–Wahrscheinlichkeiten ergibt sich $P_Z(Z)$ = [1/2; 1/2] ⇒ $H(Z)$ = 1.
- $X$ und $Z$ sind ebenfalls statistisch unabhängig, da für die 2D–PMF $P_{XZ}(X, Z)$ = $P_X(X) · P_Z(Z)$ gilt.
- Daraus folgt: $H(Z|X)$ = $H(Z)$, $H(X|Z)$ = $H(X)$, $I(X; Z)$ = 0.
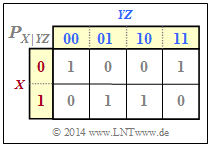
Aus der bedingten Wahrscheinlichkeitsfunktion $P_{X|YZ}$ gemäß der unteren Grafik lassen sich berechnen:
- $H(X|YZ)$ = 0, da alle $P_{X|YZ}$–Einträge entweder 0 oder 1 ⇒ bedingte Entropie,
- $I(X; YZ)$ = $H(X)$ – $H(X|YZ)$ = $H(X)$ ⇒ Transinformation,
- $I(X; Y|Z)$ = $H(X|Z)$ = $H(X)$ ⇒ bedingte Transinformation.
Im vorliegenden Beispiel ist also $I(X; Y|Z)$ = 1 (bit) größer als $I(X; Y)$ = 0 (bit).
Kettenregel der Transinformation
Bisher haben wir die Transinformation nur zwischen zwei eindimensionalen Zufallsgrößen betrachtet. Nun erweitern wir die Definition auf insgesamt $n$ + 1 Zufallsgrößen, die wir aus Darstellungsgründen mit $X_1$, ..., $X_n$ sowie $Z$ bezeichnen. Dann gilt
Kettenregel der Transinformation: Die Transinformation zwischen der $n$–dimensionalen Zufallsgröße $X_1 X_2 ... X_n$ und der Zufallsgröße $Z$ lässt sich wie folgt darstellen und berechnen:
$$\begin{align*}I(X_1\hspace{0.05cm}X_2\hspace{0.05cm}... \hspace{0.1cm}X_n;Z) \hspace{-0.15cm} & = \hspace{-0.15cm} I(X_1;Z) + I(X_2;Z | X_1) + ... \hspace{0.1cm}+ I(X_n;Z | X_1\hspace{0.05cm}X_2\hspace{0.05cm}... \hspace{0.1cm}X_{n-1}) = \\ & = \hspace{-0.15cm} \sum_{i = 1}^{n} I(X_i;Z | X_1\hspace{0.05cm}X_2\hspace{0.05cm}... \hspace{0.1cm}X_{i-1}) \hspace{0.05cm}.\end{align*}$$
Für den Beweis beschränken wir uns hier auf den Fall $n$ = 2, also auf insgesamt drei Zufallsgrößen, und ersetzen $X_1$ und $X_2$ durch $X$ und $Y$. Damit erhalten wir:
$$\begin{align*}I(X\hspace{0.05cm}Y;Z) \hspace{-0.15cm} & = & \hspace{-0.15cm} H(XY) - H(XY|Z) = \\ & = \hspace{-0.15cm} \big [ H(X)+ H(Y|X)\big ] - \big [ H(X|Z) + H(Y|XZ)\big ] =\\ & = \hspace{-0.15cm} \big [ H(X)- H(X|Z)\big ] - \big [ H(Y|X) + H(Y|XZ)\big ]=\\ & = \hspace{-0.15cm} I(X;Z) + I(Y;Z | X) \hspace{0.05cm}.\end{align*}$$
Aus dieser Gleichung erkennt man, dass die die Größenrelation $I(X Y; Z) ≥ I(X; Z)$ immer gegeben ist. Gleichheit ergibt sich für die bedingte Transinformation $I(Y; Z|X)$ = 0, also dann, wenn die Zufallsgrößen $Y$ und $Z$ für ein gegebenes $X$ statistisch unabhängig sind.
Wir betrachten die Markovkette $X → Y → Z$. Für eine solche Konstellation gilt stets das Data Processing Theorem mit der folgenden Konsequenz, die sich aus der Kettenregel der Transinformation ableiten lässt:
$$I(X;Z) \hspace{-0.15cm} \le \hspace{-0.15cm}I(X;Y ) \hspace{0.05cm},\\ I(X;Z) \hspace{-0.15cm} \le \hspace{-0.15cm} I(Y;Z ) \hspace{0.05cm}.$$
Das Theorem besagt somit:
- Man kann durch Manipulation (Processing Z) der Daten $Y$ keine zusätzliche Information über den Eingang $X$ gewinnen.
- Die Datenverarbeitung $Y → Z$ (durch einen zweiten Prozessor) dient nur dem Zweck, die Information über $X$ besser sichtbar zu machen.
Weitere Informationen zum Data Processing Theorem finden Sie in der Aufgabe A3.14.