Difference between revisions of "Aufgaben:Exercise 2.12: Non-coherent Demodulation"
m |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1088__Mod_A_2_12.png|right|frame| | + | [[File:P_ID1088__Mod_A_2_12.png|right|frame|Non-coherent <br>ASK Demodulation]] |
| − | + | Consider an amplitude modulated signal: | |
:$$ s(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$ | :$$ s(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$ | ||
| − | + | Reaching the receiver based on the channel propagation time, the signal is | |
:$$ r(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \hspace{0.05cm}.$$ | :$$ r(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \hspace{0.05cm}.$$ | ||
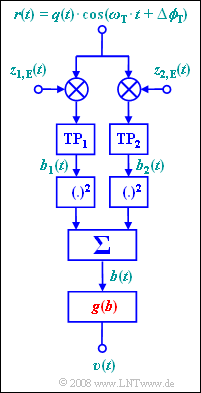
| − | + | The arrangement shown here allows perfect demodulation – that is, $v(t) = q(t)$ – without knowledge of the phase $Δϕ_T$, but only if the source signal $q(t)$ satisfies certain conditions. | |
| − | + | The two receiver-side carrier signals are: | |
:$$ z_{\rm 1, \hspace{0.08cm}E}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t) \hspace{0.05cm},$$ | :$$ z_{\rm 1, \hspace{0.08cm}E}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t) \hspace{0.05cm},$$ | ||
:$$ z_{\rm 2, \hspace{0.08cm}E}(t) = -2 \cdot \sin(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$ | :$$ z_{\rm 2, \hspace{0.08cm}E}(t) = -2 \cdot \sin(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$ | ||
| − | $\rm TP_1$ | + | $\rm TP_1$ and $\rm TP_2$ denote two ideal (rextangular) lowpass filters, each with cutoff frequency equal to the carrier frequency $f_{\rm T}$ . |
| − | + | As (digital) source signals we consider: | |
| − | * | + | * the unipolar square wave $q_1(t)$ with dimensionless amplitude values $0$ and $3$, |
| − | * | + | * the bipolar square wave signal $q_2(t)$ with the dimensionless amplitude values $±3$. |
| − | + | With respect to $s(t)$ , these two signals result in an [[Modulation_Methods/Linear_Digital_Modulation#ASK_.E2.80.93_Amplitude_Shift_Keying|ASK signal]] and a [[Modulation_Methods/Linear_Digital_Modulation#BPSK_.E2.80.93_Binary_Phase_Shift_Keying|BPSK signal]], respectively. | |
| − | + | The nonlinear function $v = g(b)$ is to be determined in this exercise. | |
| Line 32: | Line 32: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *This exercise belongs to the chapter [[Modulation_Methods/Further_AM_Variants|Further AM Variants]]. |
| − | * | + | *Particular reference is made to the page [[Modulation_Methods/Further_AM_Variants#Incoherent_.28non-coherent.29_Demodulation|Incoherent (non-coherent) Demodulation]]. |
| − | * | + | *The following trigonometric transformations are given: |
:$$ \cos(\alpha) \cdot \cos(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \big],$$ | :$$ \cos(\alpha) \cdot \cos(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \big],$$ | ||
:$$ \sin(\alpha) \cdot \sin(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)- \cos(\alpha + \beta) \big],$$ | :$$ \sin(\alpha) \cdot \sin(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)- \cos(\alpha + \beta) \big],$$ | ||
| Line 43: | Line 43: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the signals $b_1(t)$ and $b_2(t)$ in both branches – after multiplier and lowpass respectively? Which statements apply? |
|type="[]"} | |type="[]"} | ||
+ $b_1(t) = q(t) · \cos(Δϕ_{\rm T})$. | + $b_1(t) = q(t) · \cos(Δϕ_{\rm T})$. | ||
Revision as of 21:46, 22 December 2021
Consider an amplitude modulated signal:
- $$ s(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$
Reaching the receiver based on the channel propagation time, the signal is
- $$ r(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \hspace{0.05cm}.$$
The arrangement shown here allows perfect demodulation – that is, $v(t) = q(t)$ – without knowledge of the phase $Δϕ_T$, but only if the source signal $q(t)$ satisfies certain conditions.
The two receiver-side carrier signals are:
- $$ z_{\rm 1, \hspace{0.08cm}E}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t) \hspace{0.05cm},$$
- $$ z_{\rm 2, \hspace{0.08cm}E}(t) = -2 \cdot \sin(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$
$\rm TP_1$ and $\rm TP_2$ denote two ideal (rextangular) lowpass filters, each with cutoff frequency equal to the carrier frequency $f_{\rm T}$ .
As (digital) source signals we consider:
- the unipolar square wave $q_1(t)$ with dimensionless amplitude values $0$ and $3$,
- the bipolar square wave signal $q_2(t)$ with the dimensionless amplitude values $±3$.
With respect to $s(t)$ , these two signals result in an ASK signal and a BPSK signal, respectively.
The nonlinear function $v = g(b)$ is to be determined in this exercise.
Hints:
- This exercise belongs to the chapter Further AM Variants.
- Particular reference is made to the page Incoherent (non-coherent) Demodulation.
- The following trigonometric transformations are given:
- $$ \cos(\alpha) \cdot \cos(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \big],$$
- $$ \sin(\alpha) \cdot \sin(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)- \cos(\alpha + \beta) \big],$$
- $$ \sin(\alpha) \cdot \cos(\beta) = 1/2 \cdot \big[ \sin(\alpha - \beta)+ \sin(\alpha + \beta) \big] \hspace{0.05cm}.$$
Questions
Musterlösung
- $$b_1(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \cdot 2 \cdot \cos(\omega_{\rm T} \cdot t) = q(t) \cdot \cos(\Delta \phi_{\rm T})\hspace{0.05cm},$$
- $$ b_2(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}) \cdot (-2) \cdot \sin(\omega_{\rm T} \cdot t) = q(t) \cdot \sin(\Delta \phi_{\rm T})\hspace{0.05cm}.$$
- Richtig sind somit die erste und die vierte Antwort.
(2) Die Summe der Quadrate der beiden Teilsignale ergibt:
- $$ b(t) = b_1^2(t) + b_2^2(t)= q^2(t) \cdot \left( \cos^2(\Delta \phi_{\rm T})+ \sin^2(\Delta \phi_{\rm T})\right) = q^2(t)\hspace{0.05cm}.$$
Die möglichen Amplitudenwerte sind somit:
- $$b_{\rm min}\hspace{0.15cm}\underline{ = 0},$$
- $$ b_{\rm max}\hspace{0.15cm}\underline{ =9}.$$
(3) Richtig ist der zweite Lösungsvorschlag:
- $$v=g(b) = \sqrt{b} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} v(t) = \sqrt{ q^2(t) } = q(t)\hspace{0.05cm}.$$
(4) Das Ergebnis $b(t) = q^2(t)$ – siehe Teilaufgabe (2) – führt hier zum Ergebnis:
- $$b_{\rm min}\hspace{0.15cm}\underline{ = 9},$$
- $$b_{\rm max}\hspace{0.15cm}\underline{ =9}.$$
Dies zeigt, dass der hier betrachtete Demodulator nur dann funktioniert, wenn für alle Zeiten $q(t) ≥ 0$ oder $q(t) ≤ 0$ gilt und dies dem Empfänger auch bekannt ist.