Difference between revisions of "Aufgaben:Exercise 3.10Z: BSC Channel Capacity"
m (Guenter moved page Aufgabe 3.10Z: BSC–Kanalkapazität to Exercise 3.10Z: BSC Channel Capacity) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID2789__Inf_Z_3_9.png|right|frame| | + | [[File:P_ID2789__Inf_Z_3_9.png|right|frame|Entropies of the „BC” and „BSC” models]] |
| − | + | The channel capacity $C$ was defined by [https://en.wikipedia.org/wiki/Claude_Shannon Claude E. Shannon] as the maximum mutual information, whereby the maximisation refers solely to the source statistics: | |
:$$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}$$ | :$$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}$$ | ||
| − | + | In the binary channel with the probability function $P_X(X) = \big [p_0, \ p_1 \big]$ only one parameter is optimisable, for example $p_0$. The probability for a $1$ is thus also fixed: $p_1 = 1 - p_0.$ | |
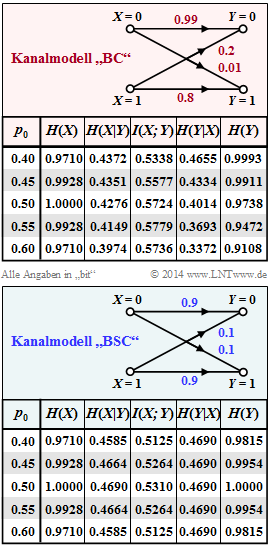
| − | + | The upper graph (reddish background) summarises the results for the [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Channel_capacity_of_a_binary_channel|asymmetric binary channel]] with $ε_0 = 0.01$ and $ε_1 = 0.2$ , which was also considered in the theory section. | |
| − | + | The maximisation leads to the result $p_0 = 0.55$ ⇒ $p_1 = 0.45$, , and one obtains for the channel capacity: | |
:$$C_{\rm BC} = \hspace{-0.05cm} \max_{P_X(X)} \hspace{0.1cm} I(X;Y) \big |_{p_0 \hspace{0.05cm} = \hspace{0.05cm}0.55} \hspace{0.05cm}=\hspace{0.05cm} 0.5779\,{\rm bit} \hspace{0.05cm}.$$ | :$$C_{\rm BC} = \hspace{-0.05cm} \max_{P_X(X)} \hspace{0.1cm} I(X;Y) \big |_{p_0 \hspace{0.05cm} = \hspace{0.05cm}0.55} \hspace{0.05cm}=\hspace{0.05cm} 0.5779\,{\rm bit} \hspace{0.05cm}.$$ | ||
| − | In | + | In the lower graph (blue background), the same information-theoretical quantities are given for the ⇒ [[Channel_Coding/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC|Binary Symmetric Channel]] (BSC) with the corruption probabilities $ε_0 = ε_1 = ε = 0.1$ , which was also assumed fore [[Aufgaben:3.10_Transinformation_beim_BSC| Exercise 3.10]] . |
| + | In the present exercise you are to | ||
| + | :* analyse the entropies $H(X)$, $H(Y)$, $H(X|Y)$ and $H(Y|X)$, | ||
| + | :* optimise the source parameter $p_0$ with respect to maximum mutual information $I(X; Y)$ , | ||
| + | :* thus determine the channel capacity $C(ε)$ , as well as | ||
| + | :* give a closed equation for $C(ε)$ by generalisation for the BSC channel model $($initially for $ε = 0.1)$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Hints: | |
| − | + | *The exercise belongs to the chapter [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung|Application to digital signal transmission]]. | |
| − | + | *Reference is made in particular to the page [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Kanalkapazit.C3.A4t_eines_Bin.C3.A4rkanals|Channel capacity of a binary channe]]. | |
| − | * | ||
| − | * | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | { Which statements are true for the conditional entropies in the BSC model? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The equivocation results in $H(X|Y) = H_{\rm bin}(ε)$. |
| − | + | + | + The irrelevance results in $H(Y|X) = H_{\rm bin}(ε)$. |
| − | - | + | - The irrelevance results in $H(Y|X) = H_{\rm bin}(p_0)$. |
| − | { | + | {Which statements are true for the channel capacity $C_{\rm BSC}$ of the BSC model? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The channel capacity is equal to the maximum transinformation. |
| − | + | + | + For the BSC, maximisation leads to the result $p_0 = p_1 = 0.5$. |
| − | + | + | + For $p_0 = p_1 = 0.5$ , $H(X) = H(Y) = 1 \ \rm bit$. |
| − | { | + | {Which channel capacity $C_{\rm BSC}$ results depending on the BSC parameter $ε$? |
|type="{}"} | |type="{}"} | ||
$ε = 0.0\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \ $ { 1 1% } $\ \rm bit$ | $ε = 0.0\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \ $ { 1 1% } $\ \rm bit$ | ||
| Line 53: | Line 51: | ||
$ε = 0.5\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \ $ { 0. } $\ \rm bit$ | $ε = 0.5\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \ $ { 0. } $\ \rm bit$ | ||
| − | { | + | {Which channel capacity $C_{\rm BSC}$ results depending on the BSC parameter $ε$? |
|type="{}"} | |type="{}"} | ||
$ε = 1.0\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \ $ { 1 1% } $\ \rm bit$ | $ε = 1.0\text{:} \hspace{0.5cm} C_{\rm BSC} \ = \ $ { 1 1% } $\ \rm bit$ | ||
| Line 61: | Line 59: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Proposed solution 2</u> is correct, as the following calculation shows: |
:$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = p_0 \cdot (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} + p_0 \cdot \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} +p_1 \cdot \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} + p_1 \cdot (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} $$ | :$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = p_0 \cdot (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} + p_0 \cdot \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} +p_1 \cdot \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} + p_1 \cdot (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} $$ | ||
:$$\Rightarrow \hspace{0.3cm} H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = (p_0 + p_1) \cdot \left [ \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} + (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} \right ] \hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm} H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = (p_0 + p_1) \cdot \left [ \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} + (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} \right ] \hspace{0.05cm}.$$ | ||
| − | * | + | *With $p_0 + p_1 = 1$ and the binary entropy function $H_{\rm bin}$ , one obtains the proposed result: $H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H_{\rm bin}(\varepsilon)\hspace{0.05cm}.$ |
| − | * | + | *For $ε = 0.1$ we get $H(Y|X) = 0.4690 \ \rm bit$. The same value stands for all $p_0$ in the given table. |
| − | * | + | *From the table one can also see that for the BSC model (blue background) as well as for the more general (asymmetric) BC model (red background) the equivocation $H(X|Y)$ depends on the source symbol probabilities $p_0$ and $p_1$ . It follows that proposed solution 1 cannot be correct. |
| − | * | + | *The irrelevance $H(Y|X)$ is independent of the source statistics, so that solution proposal 3 can also be excluded. |
| − | '''(2)''' | + | '''(2)''' <u>All given alternative solutions</u> are correct: |
| − | * | + | *The channel capacity is defined as the maximum mutual information, where the maximisation has to be done with respect to $P_X = (p_0, p_1)$ : |
:$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$ | :$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$ | ||
| − | * | + | *The equation is generally valid, i.e. also for the unbalanced binary channel highlighted in red. |
| − | * | + | *The mutual information can be calculated, for example, as $I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$, where according to subtask '''(1)''' the term $H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$ is independent of $p_0$ or $p_1 = 1- p_0$ . |
| − | * | + | *The maximum mutual information thus results exactly when the sink entropy $H(Y)$ is maximum. This is the case for $p_0 = p_1 = 0.5$: |
:$$H(X) = H(Y) = 1 \ \rm bit.$$ | :$$H(X) = H(Y) = 1 \ \rm bit.$$ | ||
| − | [[File:P_ID2790__Inf_Z_3_9_B.png|frame| | + | [[File:P_ID2790__Inf_Z_3_9_B.png|frame|Binary entropy function and BSC channel capacity]] |
| − | '''(3)''' | + | '''(3)''' According to the subtasks '''(1)''' and '''(2)''' one obtains for the BSC channel capacity: |
:$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$ | :$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$ | ||
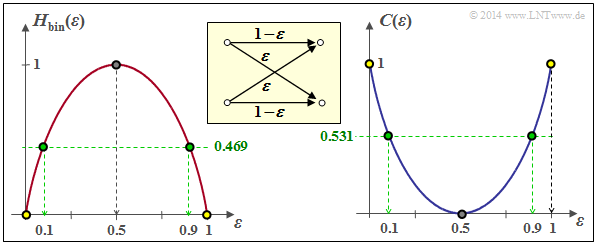
| − | + | The graph shows the binary entropy function on the left and the channel capacity on the right. One obtains: | |
| − | * | + | * for $ε = 0.0$ (error-free channel): <br> $C = 1\ \rm (bit)$ ⇒ dot with yellow filling, |
| − | * | + | * for $ε = 0.1$ (considered so far): <br> $C = 0.531\ \rm (bit)$ ⇒ dot with green filling, |
| − | * | + | * for $ε = 0.5$ (completely disturbed): <br> $C = 0\ \rm (bit)$ ⇒ dot with grey filling. |
| − | '''(4)''' | + | '''(4)''' From the graph one can see that from an information-theoretical point of view $ε = 1$ is identical to $ε = 0$ : |
:$$C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}1} \hspace{0.05cm}= C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0} \hspace{0.15cm} \underline {=1\,{\rm (bit)}} \hspace{0.05cm}.$$ | :$$C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}1} \hspace{0.05cm}= C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0} \hspace{0.15cm} \underline {=1\,{\rm (bit)}} \hspace{0.05cm}.$$ | ||
| − | * | + | *The channel only carries out a renaming here. This is called "mapping". |
| − | * | + | *Every $0$ becomes a $1$ and every $1$ becomes a $0$. Accordingly: |
:$$C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0.9} \hspace{0.05cm}= C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0.1} \hspace{0.15cm} \underline {=0.531\,{\rm (bit)}} \hspace{0.05cm}$$ | :$$C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0.9} \hspace{0.05cm}= C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0.1} \hspace{0.15cm} \underline {=0.531\,{\rm (bit)}} \hspace{0.05cm}$$ | ||
Revision as of 13:15, 14 September 2021
The channel capacity $C$ was defined by Claude E. Shannon as the maximum mutual information, whereby the maximisation refers solely to the source statistics:
- $$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}$$
In the binary channel with the probability function $P_X(X) = \big [p_0, \ p_1 \big]$ only one parameter is optimisable, for example $p_0$. The probability for a $1$ is thus also fixed: $p_1 = 1 - p_0.$
The upper graph (reddish background) summarises the results for the asymmetric binary channel with $ε_0 = 0.01$ and $ε_1 = 0.2$ , which was also considered in the theory section.
The maximisation leads to the result $p_0 = 0.55$ ⇒ $p_1 = 0.45$, , and one obtains for the channel capacity:
- $$C_{\rm BC} = \hspace{-0.05cm} \max_{P_X(X)} \hspace{0.1cm} I(X;Y) \big |_{p_0 \hspace{0.05cm} = \hspace{0.05cm}0.55} \hspace{0.05cm}=\hspace{0.05cm} 0.5779\,{\rm bit} \hspace{0.05cm}.$$
In the lower graph (blue background), the same information-theoretical quantities are given for the ⇒ Binary Symmetric Channel (BSC) with the corruption probabilities $ε_0 = ε_1 = ε = 0.1$ , which was also assumed fore Exercise 3.10 . In the present exercise you are to
- analyse the entropies $H(X)$, $H(Y)$, $H(X|Y)$ and $H(Y|X)$,
- optimise the source parameter $p_0$ with respect to maximum mutual information $I(X; Y)$ ,
- thus determine the channel capacity $C(ε)$ , as well as
- give a closed equation for $C(ε)$ by generalisation for the BSC channel model $($initially for $ε = 0.1)$.
Hints:
- The exercise belongs to the chapter Application to digital signal transmission.
- Reference is made in particular to the page Channel capacity of a binary channe.
Questions
Solution
- $$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = p_0 \cdot (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} + p_0 \cdot \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} +p_1 \cdot \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} + p_1 \cdot (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} $$
- $$\Rightarrow \hspace{0.3cm} H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = (p_0 + p_1) \cdot \left [ \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} + (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} \right ] \hspace{0.05cm}.$$
- With $p_0 + p_1 = 1$ and the binary entropy function $H_{\rm bin}$ , one obtains the proposed result: $H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H_{\rm bin}(\varepsilon)\hspace{0.05cm}.$
- For $ε = 0.1$ we get $H(Y|X) = 0.4690 \ \rm bit$. The same value stands for all $p_0$ in the given table.
- From the table one can also see that for the BSC model (blue background) as well as for the more general (asymmetric) BC model (red background) the equivocation $H(X|Y)$ depends on the source symbol probabilities $p_0$ and $p_1$ . It follows that proposed solution 1 cannot be correct.
- The irrelevance $H(Y|X)$ is independent of the source statistics, so that solution proposal 3 can also be excluded.
(2) All given alternative solutions are correct:
- The channel capacity is defined as the maximum mutual information, where the maximisation has to be done with respect to $P_X = (p_0, p_1)$ :
- $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
- The equation is generally valid, i.e. also for the unbalanced binary channel highlighted in red.
- The mutual information can be calculated, for example, as $I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$, where according to subtask (1) the term $H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$ is independent of $p_0$ or $p_1 = 1- p_0$ .
- The maximum mutual information thus results exactly when the sink entropy $H(Y)$ is maximum. This is the case for $p_0 = p_1 = 0.5$:
- $$H(X) = H(Y) = 1 \ \rm bit.$$
(3) According to the subtasks (1) and (2) one obtains for the BSC channel capacity:
- $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
The graph shows the binary entropy function on the left and the channel capacity on the right. One obtains:
- for $ε = 0.0$ (error-free channel):
$C = 1\ \rm (bit)$ ⇒ dot with yellow filling, - for $ε = 0.1$ (considered so far):
$C = 0.531\ \rm (bit)$ ⇒ dot with green filling, - for $ε = 0.5$ (completely disturbed):
$C = 0\ \rm (bit)$ ⇒ dot with grey filling.
(4) From the graph one can see that from an information-theoretical point of view $ε = 1$ is identical to $ε = 0$ :
- $$C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}1} \hspace{0.05cm}= C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0} \hspace{0.15cm} \underline {=1\,{\rm (bit)}} \hspace{0.05cm}.$$
- The channel only carries out a renaming here. This is called "mapping".
- Every $0$ becomes a $1$ and every $1$ becomes a $0$. Accordingly:
- $$C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0.9} \hspace{0.05cm}= C_{\rm BSC} \big |_{\hspace{0.05cm}\varepsilon \hspace{0.05cm} = \hspace{0.05cm}0.1} \hspace{0.15cm} \underline {=0.531\,{\rm (bit)}} \hspace{0.05cm}$$