Aufgaben:Exercise 4.12: Root-Nyquist Systems

• Return to book

Spectra of fundamental transmission pulse and base detection pulse

In quadrature amplitude modulation systems, the root-Nyquist variant is often chosen instead of a rectangular basic transmission pulse, which gets its name from the spectral range. The reason for this is the significantly smaller bandwidth.

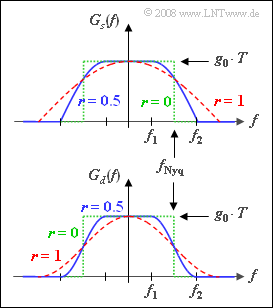
• In this case, base detection pulse  $g_d(t)$  satisfies the  first Nyquist criterion,  since  $G_d(f)$  is point-symmetric about the so-called Nyquist frequency  $f_{\rm Nyq} = 1/T$ .
• The spectral function $G_d(f)$  is a  cosine rolloff spectrum, where the rolloff factor  $r$  can take values from $0$  to  $1$  (including these limits).

Furthermore, the following holds for the Nyquist frequency response:

• When  $|f| < f_1 = f_{\rm Nyq} · (1 – r)$ ,  $G_d(f)$  is constant and equal to  $g_0 · T$.
• At frequencies greater tha  $f_2 = f_{\rm Nyq} · (1 + r)$ , $G_d(f)$  has no components.
• In between, the slope is cosine.

The optimization of digital communication systems requires that the receiver frequency response  $H_{\rm E}(f)$  should be of the same shape as the transmission spectrum $G_s(f)$ .

To obtain dimensionally correct spectral functions for this task and the graph, it is assumed that:

$$G_s(f) = \sqrt{g_0 \cdot T \cdot G_d(f)},\hspace{0.4cm} H_{\rm E}(f) = \frac{1}{g_0 \cdot T}\cdot G_s(f)\hspace{0.05cm}.$$

The top graph shows the transmission spectrum  $G_s(f)$  for the rolloff factors.

• $r = 0$   (green dotted rectangle),
• $r = 0.5$   (blue solid curve),
• $r = 1$   (red dashed curve).

Below, the spectrum   $G_d(f)$  before the decider is shown in the same colors.

• The associated impulse   $g_d(t)$  is a Nyquist impulse pulse for all valid rolloff factors   $(0 ≤ r ≤ 1)$  as opposed to the fundamental transmission pulse   $g_s(t)$.
• For this, the following equation is given in the literature - for example in  [Kam04] :

$$g_s(t) = g_0 \cdot \frac{4 r t/T \cdot \cos \left [\pi \cdot (1+r) \cdot t/T \right ]+ \sin \left [\pi \cdot (1-r) \cdot t/T \right ]}{\left [1- (4 r t/T)^2 \right ] \cdot \pi \cdot t/T}\hspace{0.05cm}.$$

Hints:

• This exercise belongs to the chapter  Quadrature Amplitude Modulation.
• Particular reference is made to the page   Nyquist and root Nyquist systems  in this chapter.
• Further useful informationen can be found in the chapter  Properties of Nyquist Systems  in the book "Digital Signal Transmission".
• [Kam04]  refers to the textbook "Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004".
• Energies are to be specified in $\rm V^2s$  ; they thus refer to the reference resistance  $R = 1 \ \rm \Omega$.

Questions

1

Wie lautet der Sendegrundimpuls  $g_s(t)$  für den Rolloff–Faktor  $r = 0$?  Welcher Signalwert ergibt sich zum Zeitpunkt  $t = 0$?

$g_s(t = 0) \ = \ $ $\ \cdot g_0$

2

Wie lautet der Sendegrundimpuls  $g_s(t)$  für den Rolloff–Faktor  $r = 1$?  Welcher Signalwert ergibt sich zum Zeitpunkt  $t = 0$?

$g_s(t = 0) \ = \ $ $\ \cdot g_0$

3

Es gelte weiter  $r = 1$.  Zu welchen Zeiten hat  $g_s(t)$  Nulldurchgänge?

	Bei allen Vielfachen der Symboldauer  $T$.
	Bei  $t = ±0.25 T, \ ±0.75 T, \ ±1.25 T, \ ±1.75 T$, ...
	Bei  $t = ±0.75 T, \ ±1.25 T,\ ±1.75 T$, ...

4

Wie lautet der Sendegrundimpuls  $g_s(t)$  für den Rolloff–Faktor  $r = 0.5$?  Welcher Signalwert ergibt sich zum Zeitpunkt  $t = 0$?

$g_s(t = 0) \ = \ $ $\ \cdot g_0$

5

Welche Aussagen sind für die Signalamplitude unabhängig von  $r$  gültig?  Lösen Sie diese Teilaufgabe im Frequenzbereich.

	Die Sendeimpulsamplitude kann alle Werte im Bereich   $0 ≤ g_s(t = 0) ≤ g_0$   annehmen.
	Die Sendeimpulsamplitude kann alle Werte im Bereich   $g_0 ≤ g_s(t = 0) ≤ 2 g_0$   annehmen.
	Die Sendeimpulsamplitude kann alle Werte im Bereich   $g_0 ≤ g_s(t = 0) ≤ 4 g_0/π$   annehmen.

6

Wie groß ist die Energie  $E_{g_s}$  des Sendegrundimpulses  $g_s(t)$  für  $r = 0$  und  $r = 1$?

$r = 0\text{:} \ \ \ \ E_{g_s} \ = \ $ $\ \cdot g_0^2 \cdot T$

$r = 1\text{:} \ \ \ \ E_{g_s} \ = \ $ $\ \cdot g_0^2 \cdot T$

Solution

Solution

(1)  Setzt man in die gegebene Gleichung  $r = 0$  ein, so verschwinden im Zähler und Nenner die jeweils ersten Terme und man erhält:

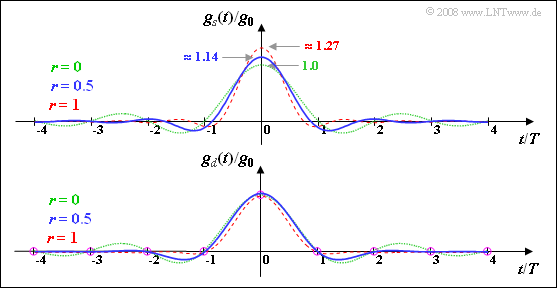
$$g_s(t) = g_0 \cdot \frac{\sin \left (\pi \cdot t/T \right )}{\pi \cdot t/T} = g_0 \cdot {\rm si} \left (\pi \cdot {t}/{T} \right )\hspace{0.05cm}.$$

• Zum Zeitpunkt  $t = 0$  ist der  $\rm si$–Impuls gleich  $g_0$:  

$$ g_s(t) \hspace{0.15cm}\underline { = 1.0 } \cdot g_0 \hspace{0.05cm}.$$

(2)  Für  $r = 1$  lässt sich die angegebene Gleichung wie folgt vereinfachen:

$$g_s(t) = \frac{4 \cdot g_0}{\pi} \cdot \frac{ \cos \left (2 \pi \cdot t/T \right )}{\left [1- (4 t/T)^2 \right ] }\hspace{0.3cm}\Rightarrow \hspace{0.3cm} g_s(t = 0) = \frac{4 \cdot g_0}{\pi} \hspace{0.15cm}\underline {= 1.273 }\cdot g_0 \hspace{0.05cm}.$$

(3)  Richtig ist der letzte Lösungsvorschlag:

• Nulldurchgänge sind für  $r = 1$  nur möglich, wenn die Cosinusfunktion im Zähler Null ist, also für alle ganzzahligen Werte von  $k$:

$$2 \pi \cdot t/T = {\pi}/{2} + k \cdot \pi \hspace{0.3cm}\Rightarrow \hspace{0.3cm} t = \pm 0.25T, \hspace{0.15cm} \pm 0.75T, \hspace{0.15cm}\pm 1.25T, \hspace{0.15cm} ...$$

• Richtig ist aber nur der letzte Lösungsvorschlag, da die Nullstellen bei  $±0.25T$  durch die Nullstelle im Nenner aufgehoben werden.
• Die Anwendung der Regel von de l'Hospital liefert  $g_s(t = ± 0.25T) = g_0$.

(4)  Mit  $r = 0.5$  und der Abkürzung  $x = t/T$  erhält man:

$$g_s(x) = \frac{g_0}{\pi} \cdot \frac{2 \cdot x \cdot \cos \left (1.5\pi \cdot x \right )+ \sin \left (0.5\pi \cdot x \right )}{\left (1- 4 \cdot x^2 \right ) \cdot x}\hspace{0.05cm}.$$

• Für die Berechnung zum Zeitpunkt  $t = 0$  muss die Regel von de l'Hospital angewandt werden.
• Die Ableitungen von Zähler und Nenner ergeben:

$$Z'(x) = 2 \cdot \cos \left (1.5\pi \cdot x \right ) - 3 \pi \cdot x \cdot \sin \left (1.5\pi \cdot x \right ) + 0.5 \pi \cdot \cos \left (0.5\pi \cdot x \right ),$$

Sendegrundimpuls (Wurzel–Nyquist) und Detektionsgrundimpuls (Nyquist)

$$N'(x) = \left (1- 4 \cdot x^2 \right ) - 8 \cdot x^2 \hspace{0.05cm}.$$

• Die beiden Grenzübergänge für  $x → 0$  liefern:

$$\lim_{x \rightarrow 0} Z'(x) = 2 +{\pi }/{2},\hspace{0.2cm} \lim_{x \rightarrow 0} N'(x) = 1 \hspace{0.05cm}.$$

• Damit gilt für die Signalamplitude zum Zeitpunkt  $t = 0$:

$$g_s(t=0) = \frac{g_0}{\pi} \cdot \left ( 2 +{\pi }/{2} \right ) = {g_0} \cdot \left ( 0.5 + {2}/{\pi } \right )\hspace{0.15cm}\underline {= 1.137} \cdot g_0 \hspace{0.05cm}.$$

Die Grafik verdeutlicht nochmals die hier berechneten Ergebnisse:

• Der Impuls  $g_d(t)$  ist ein Nyquistimpuls, das heißt, dass er zumindest bei allen Vielfachen der Symboldauer $T$ Nulldurchgänge besitzt  (je nach Rolloff–Faktor noch andere Nullstellen).
• Der Impuls  $g_s(t)$  erfüllt dagegen nicht die Nyquistbedingung.
• Außerdem erkennt man aus dieser Darstellung nochmals, dass für  $r ≠ 0$  die Impulsamplitude  $g_s(t = 0)$  stets größer als  $g_0$  ist.

(5)  Richtig ist der letzte Lösungsvorschlag  $($der erste Lösungsvorschlag scheidet bereits nach den Ergebnissen der Teilaufgaben  (2)  und  (4)  aus$)$.  Die Gültigkeit der unteren Schranke  $g_0$  und der oberen Schranke  $4g_0/π$  lässt sich wie folgt nachweisen:

• Die Impulsamplitude  $g_s(t = 0)$  ist grundsätzlich gleich der Fläche unter der Spektralfunktion  $G_s(f)$.
• Die kleinste Fläche ergibt sich für  $r = 0$.  Hier ist  $G_s(f) = g_0 · T$  im Bereich  $|f| < ±1/(2T)$.  Die Fläche ist somit gleich  $g_0$.
• Die größte Fläche ergibt sich für  $r = 1$.  Hier ist  $G_s(f)$  auf den Bereich  $±1/T$  ausgedehnt und hat einen cosinusförmigen Verlauf.
• Das Ergebnis  $g_s(t = 0) = 4g_0/π$  wurde bereits in Teilaufgabe  (3)  berechnet.  Es gilt aber auch:

$$g_s(t=0) = 2 \cdot {g_0} \cdot \int_{ 0 }^{1/T} {\cos\left(\frac{\pi }{2}\cdot f \cdot T \right)}\hspace{0.1cm} {\rm d}f = \frac{4 g_0}{\pi} \cdot \int_{ 0 }^{\pi/2} {\cos\left(x \right)}\hspace{0.1cm} {\rm d}x = {4 g_0}/{\pi} \cdot \big[\sin(\pi/2) - \sin(0) \big] = {4 g_0}/{\pi}\hspace{0.05cm}.$$

(6)  Die Energie des Sendegrundimpulses  $g_s(t)$  kann man nach dem Satz von Parseval im Zeit– oder auch im Frequenzbereich ermitteln:

$$E_{g_s} = \int_{ -\infty }^{+\infty} {[g_s(t)]^2}\hspace{0.1cm} {\rm d}t = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$

• Aus den Gleichungen und der Grafik auf der Angabenseite erkennt man, dass  $|G_s(f)|^2$  formgleich mit  $G_d(f)$  ist, mit dem Unterschied, dass die Höhe nun  $(g_0 · T)^2$  anstelle von  $g_0 · T$  ist:

$$E_{g_s} = \int_{ -\infty }^{+\infty} {|G_s(f)|^2}\hspace{0.1cm} {\rm d}f = \frac{g_0^2 \cdot T^2}{g_0 \cdot T} \cdot \int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f \hspace{0.05cm}.$$

• Aufgrund der Nyquistform von  $G_d(f)$  gilt aber unabhängig von  $r$:

$$\int_{ -\infty }^{+\infty} {G_d(f)}\hspace{0.1cm} {\rm d}f = g_0 \hspace{0.05cm}.$$

• Damit ist auch die Impulsenergie unabhängig von  $r$, also auch gültig für  $r = 0$  und  $r = 1$.  In  beiden Fällen  ist  $E_ {g_s}\hspace{0.15cm}\underline { = 1.0} · g_0^2 · T.$