Difference between revisions of "Aufgaben:Exercise 4.7: Several Parallel Gaussian Channels"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Informationstheorie/AWGN–Kanalkapazität bei wertkontinuierlichem Eingang }} right| Die Kanal…“) |
|||
| (33 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/AWGN_Channel_Capacity_for_Continuous_Input |
}} | }} | ||
| − | [[File:P_ID2905__Inf_A_4_7_neu.png|right|]] | + | [[File:P_ID2905__Inf_A_4_7_neu.png|right|frame|Signal space points in digital modulation]] |
| − | + | The channel capacity of the AWGN channel with the indicator $Y = X + N$ was given in the [[Information_Theory/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang#Channel_capacity_of_the_AWGN_channels|theory section]] as follows <br>(with the additional unit "bit"): | |
| − | : | + | :$$C_{\rm AWGN}(P_X,\ P_N) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right )\hspace{0.05cm}.$$ |
| − | $$C_{\rm AWGN}(P_X) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + | + | The quantities used have the following meaning: |
| − | + | * $P_X$ is the transmission power ⇒ variance of the random variable $X$, | |
| − | + | * $P_N$ is the noise power ⇒ variance of the random variable $N$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | If $K$ identical Gaussian channels are used in parallel, the total capacity is: | |
| − | : | + | :$$C_K(P_X,\ P_N) = K \cdot C_{\rm AWGN}(P_X/K, \ P_N) \hspace{0.05cm}.$$ |
| − | + | Here it is considered that | |
| − | + | * in each channel the same interference power $P_N$ is present, | |
| − | + | * thus each channel receives the same transmit power $(P_X/K)$ , | |
| − | + | * the total power is equal to $P_X$ exactly as in the case $K = 1$ . | |
| − | |||
| − | + | In the adjacent graph, the signal space points for some digital modulation schemes are given: | |
| − | === | + | * [[Modulation_Methods/Linear_Digital_Modulation#ASK_.E2.80.93_Amplitude_Shift_Keying|Amplitude Shift Keying]] (ASK), |
| + | * [[Modulation_Methods/Linear_Digital_Modulation#BPSK_.E2.80.93_Binary_Phase_Shift_Keying|Binary Phase Shift Keying]] (BPSK), | ||
| + | * [[Modulation_Methods/Further_AM_Variants#Quadrature_Amplitude_Modulation_.28QAM.29|Quadrature Amplitude Modulation]] (here: 4-QAM), | ||
| + | *[[Examples_of_Communication_Systems/Further_Developments_of_the_GSM#Enhanced_Data_Rates_for_GSM_Evolution|Phase Shift Keying]] (here: 8–PSK for GSM Evolution), | ||
| + | * [[Modulation_Methods/Quadrature_Amplitude_Modulation#Other_signal_space_constellations|Combined ASK/PSK Modulation]] (here: 16-ASK/PSK). | ||
| + | |||
| + | |||
| + | At the beginning of this exercise, check which $K$–parameter is valid for each method. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Information_Theory/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang|AWGN channel capacity with continuous value input]]. | ||
| + | *Reference is made in particular to the page [[Information_Theory/AWGN_Channel_Capacity_for_Continuous_Input#Parallel_Gaussian_channels|Parallel Gaussian Channels]]. | ||
| + | *Since the results are to be given in "bit", wird "log<sub>2</sub>" is used. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | |
| − | |type=" | + | {Which parameters $K$ are valid for the following modulation methods? |
| − | - | + | |type="{}"} |
| − | + | + | $K \ = \ $ { 1 3% } $\text{ (ASK)}$ |
| + | $K \ = \ $ { 1 3% } $\text{ (BPSK)}$ | ||
| + | $K \ = \ $ { 2 3% } $\text{ (4-QAM)}$ | ||
| + | $K \ = \ $ { 2 3% } $\text{ (8-PSK)}$ | ||
| + | $K \ = \ $ { 2 3% } $\text{ (16-ASK/PSK)}$ | ||
| + | |||
| + | |||
| + | |||
| + | {What is the channel capacity $C_K$ for $K$ equal channels, each with the noise power $P_N$ and the transmission power $P_X(K)$? | ||
| + | |type="()"} | ||
| + | - $C_K = K/2 \cdot \log_2 \ \big[1 + P_X/P_N \big]$. | ||
| + | + $C_K = K/2 \cdot \log_2 \ \big[1 + P_X/(K \cdot P_N) \big]$. | ||
| + | - $C_K = 1/2 \cdot \log_2 \ \big[1 + P_X/P_N \big]$. | ||
| + | |||
| + | |||
| − | { | + | {What are the capacities for $P_X/P_N = 15$? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $K = 1\text{:} \ \ C_K \ = \ $ { 2 3% } $\ \rm bit$ |
| + | $K = 2\text{:} \ \ C_K \ = \ $ { 3.087 3% } $\ \rm bit$ | ||
| + | $K = 4\text{:} \ \ C_K \ = \ $ { 4.496 3% } $\ \rm bit$ | ||
| + | |||
| + | |||
| + | |||
| + | {Is there a (theoretical) optimum with respect to the number $K$ of channels? | ||
| + | |type="[]"} | ||
| + | - Yes: The largest channel capacity results for $K = 2$. | ||
| + | - Yes: The largest channel capacity results for $K = 4$. | ||
| + | + No: The larger $K$, the larger the channel capacity. | ||
| + | + The limit value for $K \to \infty$ (in bit) is $C_K = P_X/P_N/2/\ln (2)$ in "bit". | ||
| + | |||
| Line 45: | Line 88: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' The parameter $K$ is equal to the dimension of the signal space representation: |
| − | '''2 | + | * For <u>ASK and BPSK</u>, $\underline{K=1}$. |
| − | + | * For <u> constellations 3 to 5</u>, however, $\underline{K=2}$ (orthogonal modulation with cosine and sine). | |
| − | '''4. | + | |
| − | + | ||
| − | ''' | + | |
| − | + | '''(2)''' Correct is the <u>proposed solution 2</u>: | |
| + | *For each of the channels $(1 ≤ k ≤ K)$, the channel capacitance is $C = 1/2 \cdot \log_2 \ \big[1 + (P_X/K) /P_N) \big]$. | ||
| + | *The total capacitance is then larger by a factor of $K$ : | ||
| + | :$$C_K(P_X) = \sum_{k= 1}^K \hspace{0.1cm}C_k = \frac{K}{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{K \cdot P_N} \right )\hspace{0.05cm}.$$ | ||
| + | *The proposed solution 1 is too positive. This would apply when limiting the total power to $K · P_X$ . | ||
| + | *Proposition 3 would imply that no capacity increase is achieved by using multiple independent channels, which is obviously not true. | ||
| + | |||
| + | |||
| + | [[File:P_ID2902__Inf_A_4_7c.png|right|frame|Channel capacity $C_K$ of $K$ parallel Gaussian channels for different $\xi = P_X/P_N$]] | ||
| + | '''(3)''' The table shows the results for $K = 1$, $K = 2$ and $K = 4$, and various signa–to–noise power ratios $\xi = P_X/P_N$. <br>For $\xi = P_X/P_N = 15$ (highlighted column), the result is: | ||
| + | |||
| + | * $K=1$: $C_K = 1/2 · \log_2 \ (16)\hspace{0.05cm}\underline{ = 2.000}$ bit, | ||
| + | * $K=2$: $C_K = 1/2 · \log_2 \ (8.5)\hspace{0.05cm}\underline{ = 3.087}$ bit, | ||
| + | * $K=4$: $C_K = 1/2 · \log_2 \ (4.75)\hspace{0.05cm}\underline{ = 4.496}$ bit. | ||
| + | <br clear=all> | ||
| + | '''(4)''' <u>Propositions 3 and 4</u> are correct, as the following calculations show: | ||
| + | *It is already obvious from the above table that the first proposed solution must be wrong. | ||
| + | *We now write the channel capacity using the natural logarithm and the abbreviation $\xi = P_X/P_N$: | ||
| + | :$$C_{\rm nat}(\xi, K) ={K}/{2} \cdot {\rm ln}\hspace{0.05cm}\left ( 1 + {\xi}/{K} \right )\hspace{0.05cm}.$$ | ||
| + | *Then, for large values of $K$ i.e., for small values of the quotient $\varepsilon =\xi/K$ holds: | ||
| + | :$${\rm ln}\hspace{0.05cm}\left ( 1 + \varepsilon \right )= | ||
| + | \varepsilon - \frac{\varepsilon^2}{2} + \frac{\varepsilon^3}{3} - ... | ||
| + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | C_{\rm nat}(\xi, K) = \frac{K}{2} \cdot \left [ \frac{\xi}{K} - \frac{\xi^2}{2K^2} + | ||
| + | \frac{\xi^3}{3K^3} - \text{...} \right ]$$ | ||
| + | :$$\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | C_{\rm bit}(\xi, K) = \frac{\xi}{2 \cdot {\rm ln}\hspace{0.1cm}(2)} \cdot \left [ 1 - \frac{\xi}{2K} + | ||
| + | \frac{\xi^2}{3K^2} -\frac{\xi^3}{4K^3} + | ||
| + | \frac{\xi^4}{5K^4} - \text{...} \right ] \hspace{0.05cm}.$$ | ||
| + | * For $K → ∞$ , the proposed value is: | ||
| + | :$$C_{\rm bit}(\xi, K \rightarrow\infty) = \frac{\xi}{2 \cdot {\rm ln}\hspace{0.1cm}(2)} = | ||
| + | \frac{P_X/P_N}{2 \cdot {\rm ln}\hspace{0.1cm}(2)} \hspace{0.05cm}.$$ | ||
| + | *For smaller values of $K$, the result is always a smaller $C$–value, since | ||
| + | :$$\frac{\xi}{2K} > \frac{\xi^2}{3K^2}\hspace{0.05cm}, \hspace{0.5cm} | ||
| + | \frac{\xi^3}{4K^3} > \frac{\xi^4}{5K^4} \hspace{0.05cm}, \hspace{0.5cm} {\rm usw.}$$ | ||
| + | |||
| + | The last row of the table shows: With $K = 4$ one is still far away from the theoretical maximum $($for $K → ∞)$ for large $\xi$–values. | ||
| + | |||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^4.2 AWGN and Value-Continuous Input^]] |
Latest revision as of 14:33, 4 October 2021
The channel capacity of the AWGN channel with the indicator $Y = X + N$ was given in the theory section as follows
(with the additional unit "bit"):
- $$C_{\rm AWGN}(P_X,\ P_N) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right )\hspace{0.05cm}.$$
The quantities used have the following meaning:
- $P_X$ is the transmission power ⇒ variance of the random variable $X$,
- $P_N$ is the noise power ⇒ variance of the random variable $N$.
If $K$ identical Gaussian channels are used in parallel, the total capacity is:
- $$C_K(P_X,\ P_N) = K \cdot C_{\rm AWGN}(P_X/K, \ P_N) \hspace{0.05cm}.$$
Here it is considered that
- in each channel the same interference power $P_N$ is present,
- thus each channel receives the same transmit power $(P_X/K)$ ,
- the total power is equal to $P_X$ exactly as in the case $K = 1$ .
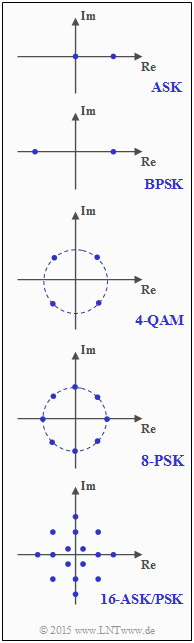
In the adjacent graph, the signal space points for some digital modulation schemes are given:
- Amplitude Shift Keying (ASK),
- Binary Phase Shift Keying (BPSK),
- Quadrature Amplitude Modulation (here: 4-QAM),
- Phase Shift Keying (here: 8–PSK for GSM Evolution),
- Combined ASK/PSK Modulation (here: 16-ASK/PSK).
At the beginning of this exercise, check which $K$–parameter is valid for each method.
Hints:
- The exercise belongs to the chapter AWGN channel capacity with continuous value input.
- Reference is made in particular to the page Parallel Gaussian Channels.
- Since the results are to be given in "bit", wird "log2" is used.
Questions
Solution
- For ASK and BPSK, $\underline{K=1}$.
- For constellations 3 to 5, however, $\underline{K=2}$ (orthogonal modulation with cosine and sine).
(2) Correct is the proposed solution 2:
- For each of the channels $(1 ≤ k ≤ K)$, the channel capacitance is $C = 1/2 \cdot \log_2 \ \big[1 + (P_X/K) /P_N) \big]$.
- The total capacitance is then larger by a factor of $K$ :
- $$C_K(P_X) = \sum_{k= 1}^K \hspace{0.1cm}C_k = \frac{K}{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{K \cdot P_N} \right )\hspace{0.05cm}.$$
- The proposed solution 1 is too positive. This would apply when limiting the total power to $K · P_X$ .
- Proposition 3 would imply that no capacity increase is achieved by using multiple independent channels, which is obviously not true.
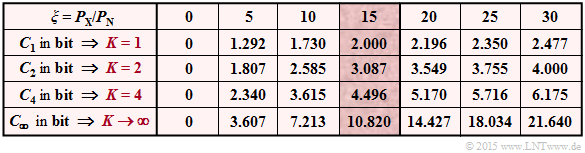
(3) The table shows the results for $K = 1$, $K = 2$ and $K = 4$, and various signa–to–noise power ratios $\xi = P_X/P_N$.
For $\xi = P_X/P_N = 15$ (highlighted column), the result is:
- $K=1$: $C_K = 1/2 · \log_2 \ (16)\hspace{0.05cm}\underline{ = 2.000}$ bit,
- $K=2$: $C_K = 1/2 · \log_2 \ (8.5)\hspace{0.05cm}\underline{ = 3.087}$ bit,
- $K=4$: $C_K = 1/2 · \log_2 \ (4.75)\hspace{0.05cm}\underline{ = 4.496}$ bit.
(4) Propositions 3 and 4 are correct, as the following calculations show:
- It is already obvious from the above table that the first proposed solution must be wrong.
- We now write the channel capacity using the natural logarithm and the abbreviation $\xi = P_X/P_N$:
- $$C_{\rm nat}(\xi, K) ={K}/{2} \cdot {\rm ln}\hspace{0.05cm}\left ( 1 + {\xi}/{K} \right )\hspace{0.05cm}.$$
- Then, for large values of $K$ i.e., for small values of the quotient $\varepsilon =\xi/K$ holds:
- $${\rm ln}\hspace{0.05cm}\left ( 1 + \varepsilon \right )= \varepsilon - \frac{\varepsilon^2}{2} + \frac{\varepsilon^3}{3} - ... \hspace{0.3cm}\Rightarrow \hspace{0.3cm} C_{\rm nat}(\xi, K) = \frac{K}{2} \cdot \left [ \frac{\xi}{K} - \frac{\xi^2}{2K^2} + \frac{\xi^3}{3K^3} - \text{...} \right ]$$
- $$\hspace{0.3cm}\Rightarrow \hspace{0.3cm} C_{\rm bit}(\xi, K) = \frac{\xi}{2 \cdot {\rm ln}\hspace{0.1cm}(2)} \cdot \left [ 1 - \frac{\xi}{2K} + \frac{\xi^2}{3K^2} -\frac{\xi^3}{4K^3} + \frac{\xi^4}{5K^4} - \text{...} \right ] \hspace{0.05cm}.$$
- For $K → ∞$ , the proposed value is:
- $$C_{\rm bit}(\xi, K \rightarrow\infty) = \frac{\xi}{2 \cdot {\rm ln}\hspace{0.1cm}(2)} = \frac{P_X/P_N}{2 \cdot {\rm ln}\hspace{0.1cm}(2)} \hspace{0.05cm}.$$
- For smaller values of $K$, the result is always a smaller $C$–value, since
- $$\frac{\xi}{2K} > \frac{\xi^2}{3K^2}\hspace{0.05cm}, \hspace{0.5cm} \frac{\xi^3}{4K^3} > \frac{\xi^4}{5K^4} \hspace{0.05cm}, \hspace{0.5cm} {\rm usw.}$$
The last row of the table shows: With $K = 4$ one is still far away from the theoretical maximum $($for $K → ∞)$ for large $\xi$–values.