Difference between revisions of "Channel Coding/Channel Models and Decision Structures"
| Line 17: | Line 17: | ||
| − | [[File: | + | [[File:EN_KC_T_1_2_S1.png|right|frame|PDF of the AWGN Channel|class=fit]] |
The graph on the right shows (in blue and red respectively) the conditional probability density functions: | The graph on the right shows (in blue and red respectively) the conditional probability density functions: | ||
| Line 54: | Line 54: | ||
The AWGN–channel model is not a digital channel model as we have presupposed in the paragraph [[Channel_Coding/Zielsetzung_der_Kanalcodierung#Blockschaltbild_und_Voraussetzungen|block diagram and prerequisities]] for the introductory description of channel coding methods. However, if we take into account a hard decision, we arrive at the digital model <i>Binary Symmetric Channel</i> (BSC):<br> | The AWGN–channel model is not a digital channel model as we have presupposed in the paragraph [[Channel_Coding/Zielsetzung_der_Kanalcodierung#Blockschaltbild_und_Voraussetzungen|block diagram and prerequisities]] for the introductory description of channel coding methods. However, if we take into account a hard decision, we arrive at the digital model <i>Binary Symmetric Channel</i> (BSC):<br> | ||
| − | [[File: | + | [[File:EN_KC_T_1_2_S2.png|center|frame|BSC–Model and relation with The AWGN Model|class=fit]] |
Choosing the falsification probabilities ${\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x=0)$ respectively, ${\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x=1)$ respectively to be | Choosing the falsification probabilities ${\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x=0)$ respectively, ${\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x=1)$ respectively to be | ||
| Line 84: | Line 84: | ||
The BSC–model only provides the statements "correct" and "incorrect". However, some receivers– such as the so-called [[Channel_Coding/Soft-in_Soft-Out_Decoder#Hard_Decision_vs._Soft_Decision|Soft–in Soft–out Decoder]] – can also provide some information about the certainty of the decision, although they must of course be informed about which of their input values are certain and which are rather uncertain.<br> | The BSC–model only provides the statements "correct" and "incorrect". However, some receivers– such as the so-called [[Channel_Coding/Soft-in_Soft-Out_Decoder#Hard_Decision_vs._Soft_Decision|Soft–in Soft–out Decoder]] – can also provide some information about the certainty of the decision, although they must of course be informed about which of their input values are certain and which are rather uncertain.<br> | ||
| − | [[File: | + | [[File:EN_KC_T_1_2_S3.png|center|frame|Binary Erasure Channel (BEC) and connection with the AWGN model|class=fit]] |
The <i>Binary Erasure Channel</i> (BEC) provides such information. On the basis of the graph you can see: | The <i>Binary Erasure Channel</i> (BEC) provides such information. On the basis of the graph you can see: | ||
*The input alphabet of the BEC–channel model is binary ⇒ $x ∈ \{0, \hspace{0.05cm}1\}$ and the output alphabet is ternary ⇒ $y ∈ \{0, \hspace{0.05cm}1, \hspace{0.05cm}\rm E\}$. A $\rm E$ denotes an uncertain decision. This new "symbol" stands for <i>Erasure</i>. | *The input alphabet of the BEC–channel model is binary ⇒ $x ∈ \{0, \hspace{0.05cm}1\}$ and the output alphabet is ternary ⇒ $y ∈ \{0, \hspace{0.05cm}1, \hspace{0.05cm}\rm E\}$. A $\rm E$ denotes an uncertain decision. This new "symbol" stands for <i>Erasure</i>. | ||
| Line 111: | Line 111: | ||
can be modeled. As with the BEC–model, $x ∈ \{0, \hspace{0.05cm}1\}$ and $y ∈ \{0, \hspace{0.05cm}1, \hspace{0.05cm}\rm E\}$.<br> | can be modeled. As with the BEC–model, $x ∈ \{0, \hspace{0.05cm}1\}$ and $y ∈ \{0, \hspace{0.05cm}1, \hspace{0.05cm}\rm E\}$.<br> | ||
| − | [[File: | + | [[File:EN_KC_T_1_2_S4.png|center|frame|Binary Symmetric Error & Erasure Channel (BSEC) & connection with the AWGN model|class=fit]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| Line 130: | Line 130: | ||
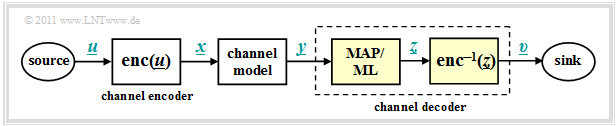
We now start from the model sketched below and apply the methods already described in chapter [[Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver| structure of the optimal receiver]] of the book "Digital Signal Transmission" to the decoding process.<br> | We now start from the model sketched below and apply the methods already described in chapter [[Digital_Signal_Transmission/Structure_of_the_Optimal_Receiver| structure of the optimal receiver]] of the book "Digital Signal Transmission" to the decoding process.<br> | ||
| − | [[File: | + | [[File:EN_KC_T_1_2_S5.png|center|frame|Model for the description of MAP and ML decoding|class=fit]] |
The task of the channel decoder (or channel decoder) is to determine the vector $\underline{v}$ so that it matches the information word $\underline{u}$ "as well as possible". | The task of the channel decoder (or channel decoder) is to determine the vector $\underline{v}$ so that it matches the information word $\underline{u}$ "as well as possible". | ||
Revision as of 17:31, 2 June 2022
Contents
- 1 AWGN channel at Binary Input
- 2 Binary Symmetric Channel – BSC
- 3 Binary Erasure Channel – BEC
- 4 Binary Symmetric Error & Erasure Channel – BSEC
- 5 Maximum-a-posteriori– and Maximum-Likelihood–criterion
- 6 Definitions of the different optimal receivers
- 7 Maximum likelihood decision at the BSC channel
- 8 Maximum likelihood decision at the AWGN channel
- 9 Exercises for the chapter
AWGN channel at Binary Input
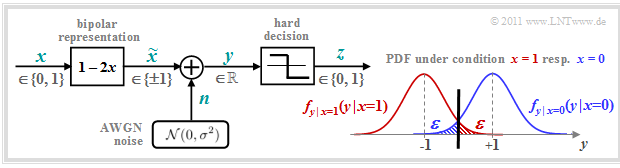
We consider the well-known discrete-time AWGN Channel model according to the lower left graph:
- The binary and discrete-time message signal $x$ takes the values $0$ and $1$ with equal probability; that is, it is ${\rm Pr}(x = 0) = {\rm Pr}(\tilde{x} =+1) = 1/2$ and ${\rm Pr}(x = 1) = {\rm Pr}(\tilde{x} =-1) = 1/2$.
- Transmission is affected by additive white gaussian noise (AWGN) $n$ with the (normalised) noise power $\sigma^2 = N_0/E_{\rm B}$ . The dispersion of the Gaussian–WDF is $\sigma$.
- Because of the Gaussian WDF, the output signal $y = \tilde{x} +n$ can take on any real value in the range $-\infty$ to $+\infty$ . The signal value $y$ is therefore discrete in time like $x$ $($bzw. $\tilde{x})$ but in contrast to the latter it is continuous in value.
The graph on the right shows (in blue and red respectively) the conditional probability density functions:
- \[f_{y \hspace{0.03cm}| \hspace{0.03cm}x=0 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=0 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e}^{ - (y-1)^2/(2\sigma^2) }\hspace{0.05cm},\]
- \[f_{y \hspace{0.03cm}| \hspace{0.03cm}x=1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e}^{ - (y+1)^2/(2\sigma^2) }\hspace{0.05cm}.\]
Not shown is the total (unconditional) WDF, for which applies in the case of equally probable symbols:
- \[f_y(y) = {1}/{2} \cdot \left [ f_{y \hspace{0.03cm}| \hspace{0.03cm}x=0 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=0 ) + f_{y \hspace{0.03cm}| \hspace{0.03cm}x=1 } \hspace{0.05cm} (y \hspace{0.05cm}| \hspace{0.05cm}x=1 )\right ]\hspace{0.05cm}.\]
The two shaded areas $($each $\varepsilon)$ mark decision errors under the condition $x=0$ ⇒ $\tilde{x} = +1$ (blue) and respectively $x=1$ ⇒ $\tilde{x} = -1$ (red) when hard decisions are made:
- \[z = \left\{ \begin{array}{c} 0\\ 1 \end{array} \right.\quad \begin{array}{*{1}c} {\rm if} \hspace{0.15cm} y > 0\hspace{0.05cm},\\ {\rm if} \hspace{0.15cm}y < 0\hspace{0.05cm}.\\ \end{array}\]
For equally probable input symbols, the mean bit error probability ${\rm Pr}(z \ne x)$ is then also equal $\varepsilon$. With the complementary gaussian error integral ${\rm Q}(x)$ the following holds:
- \[\varepsilon = {\rm Q}(1/\sigma) = {\rm Q}(\sqrt{\rho}) = \frac {1}{\sqrt{2\pi} } \cdot \int_{\sqrt{\rho}}^{\infty}{\rm e}^{- \alpha^2/2} \hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.\]
where $\rho = 1/\sigma^2 = 2 \cdot E_{\rm S}/N_0$ denotes the signal–to–noise ratio (SNR) before the decision maker, using the following system quantities:
- $E_{\rm S}$ is the signal energy per symbol (without coding equal $E_{\rm B}$, thus equal to the signal energy per bit),
- $N_0$ denotes the constant (one-sided) noise power density of the AWGN–channel.
Notes: The presented facts are clarified with the interactive applet Symbol error probability of digital systems
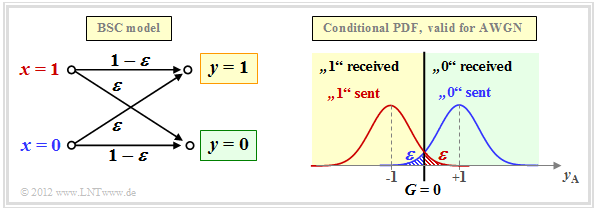
Binary Symmetric Channel – BSC
The AWGN–channel model is not a digital channel model as we have presupposed in the paragraph block diagram and prerequisities for the introductory description of channel coding methods. However, if we take into account a hard decision, we arrive at the digital model Binary Symmetric Channel (BSC):
Choosing the falsification probabilities ${\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x=0)$ respectively, ${\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x=1)$ respectively to be
- \[\varepsilon = {\rm Q}(\sqrt{\rho})\hspace{0.05cm},\]
then the connection to the AWGN–Kanalmodell is established. The decision boundary is at $G = 0$, which also gives rise to the property "symmetrical".
Note: In the AWGN–model, we have denoted the binary output (after threshold decision) as $z \in \{0, \hspace{0.05cm}1\}$ . For the digital channel models (BSC, BEC, BSEC), we now denote the discrete value output again by $y$. To avoid confusion, we now call the output signal of the AWGN–model $y_{\rm A}$. For the analog receive signal then $y_{\rm A} = \tilde{x} +n$.
The BSC–model provides a statistically independent error sequence and is thus suitable for modeling memoryless zero feedback channels, which are considered without exception in this book.
For the description of memory-affected channels, other models must be used, which are discussed in the fifth main chapter of the book "Digital Signal Transmission", for example, bundle error channels according to the
$\text{Example 1:}$ The figure shows
- statistically independent errors according to the BSC–model (left), and
- so-called burst errors according to Gilbert–Elliott (right).
The bit error rate is $10\%$ in both cases. From the right graph it can be seen from the burst noise that the image was transmitted line by line.
Binary Erasure Channel – BEC
The BSC–model only provides the statements "correct" and "incorrect". However, some receivers– such as the so-called Soft–in Soft–out Decoder – can also provide some information about the certainty of the decision, although they must of course be informed about which of their input values are certain and which are rather uncertain.
The Binary Erasure Channel (BEC) provides such information. On the basis of the graph you can see:
- The input alphabet of the BEC–channel model is binary ⇒ $x ∈ \{0, \hspace{0.05cm}1\}$ and the output alphabet is ternary ⇒ $y ∈ \{0, \hspace{0.05cm}1, \hspace{0.05cm}\rm E\}$. A $\rm E$ denotes an uncertain decision. This new "symbol" stands for Erasure.
- Bit errors are excluded by the BEC–model per se. An unsafe decision $\rm (E)$ is made with probability $\lambda$, while the probability for a correct (and at the same time safe) decision is $1-\lambda$ .
- In the upper right, the relationship between BEC– and AWGN–channel model is shown, with the erasure–decision area $\rm (E)$ highlighted in gray. In contrast to the BSC–model, there are now two decision boundaries $G_0 = G$ and $G_1 = -G$. It holds:
- \[\lambda = {\rm Q}\big[\sqrt{\rho} \cdot (1 - G)\big]\hspace{0.05cm}.\]
We refer here again to the following applets:
Binary Symmetric Error & Erasure Channel – BSEC
The BEC–model $($error probability $0)$ is rather unrealistic and only an approximation for an extremely large signal–to–noise–power ratio (SNR for short) $\rho$.
More severe disturbances ⇒ a smaller $\rho$ would be better served by the Binary Symmetric Error & Erasure Channel (BSEC) with the two parameters
- Falsification probability $\varepsilon = {\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x=0)= {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x=1)$,
- Erasure–Probability $\lambda = {\rm Pr}(y = {\rm E}\hspace{0.05cm}|\hspace{0.05cm} x=0)= {\rm Pr}(y = {\rm E}\hspace{0.05cm}|\hspace{0.05cm} x=1)$
can be modeled. As with the BEC–model, $x ∈ \{0, \hspace{0.05cm}1\}$ and $y ∈ \{0, \hspace{0.05cm}1, \hspace{0.05cm}\rm E\}$.
$\text{Example 2:}$ We consider the BSEC–model with the two decision lines $G_0 = G = 0.5$ and $G_1 = -G = -0.5$, whose parameters $\varepsilon$ and $\lambda$ are fixed by the SNR $\rho=1/\sigma^2$ of the comparable AWGN–channel. Then
- for $\sigma = 0.5$ ⇒ $\rho = 4$:
- \[\varepsilon = {\rm Q}\big[\sqrt{\rho} \cdot (1 + G)\big] = {\rm Q}(3) \approx 0.14\%\hspace{0.05cm},\hspace{0.6cm} {\it \lambda} = {\rm Q}\big[\sqrt{\rho} \cdot (1 - G)\big] - \varepsilon = {\rm Q}(1) - {\rm Q}(3) \approx 15.87\% - 0.14\% = 15.73\%\hspace{0.05cm},\]
- for $\sigma = 0.25$ ⇒ $\rho = 16$:
- \[\varepsilon = {\rm Q}(6) \approx 10^{-10}\hspace{0.05cm},\hspace{0.6cm} {\it \lambda} = {\rm Q}(2) \approx 2.27\%\hspace{0.05cm}.\]
For the PDF shown on the right, $\rho = 4$ was assumed. For $\rho = 16$ the BSEC–model could be replaced by the simpler BEC–variant without serious differences.
Maximum-a-posteriori– and Maximum-Likelihood–criterion
We now start from the model sketched below and apply the methods already described in chapter structure of the optimal receiver of the book "Digital Signal Transmission" to the decoding process.
The task of the channel decoder (or channel decoder) is to determine the vector $\underline{v}$ so that it matches the information word $\underline{u}$ "as well as possible".
$\text{Formulated a little more precisely:}$
- It shall minimize the block error probability ${\rm Pr(block \:error)} = {\rm Pr}(\underline{v} \ne \underline{u}) $ related to the vectors $\underline{u}$ and $\underline{v}$ of length $k$ .
- Because of the unique assignment $\underline{x} = {\rm enc}(\underline{u})$ by the channel encoder or receiver side $\underline{v} = {\rm enc}^{-1}(\underline{z})$ applies in the same way:
- \[{\rm Pr(block \:error)} = {\rm Pr}(\underline{z} \ne \underline{x})\hspace{0.05cm}. \]
The channel decoder in the above model consists of two parts:
- The code word estimator determines from the receive vector $\underline{y}$ an estimate $\underline{z} \in \mathcal{C}$ according to a given criterion.
- From the (received) codeword $\underline{z}$ the information word $\underline{v}$ is determinedby simple mapping . This should match $\underline{u}$ .
There are a total of four different variants for the codeword estimator, viz.
- the maximum–a–posteriori–receiver (MAP receiver) for the entire codeword $\underline{x}$,
- the maximum–a–posteriori–receiver (MAP receiver) for the individual code bits $x_i$,
- the maximum–likelihood–receiver (ML receiver) for the entire codeword $\underline{x}$,
- the maximum–likelihood–receiver (ML receiver) for the individual code bits $x_i$.
Their definitions follow on the next page. First of all, however, the essential distinguishing feature between MAP and ML:
$\text{Conclusion:}$
- A MAP–receiver, in contrast to the ML–receiver, also considers different occurrence probabilities for the entire codeword or for their individual bits.
- If all codewords $\underline{x}$ and thus all bits $x_i$ of the codewords are equally probable, the simpler ML–receiver is equivalent to the corresponding MAP–receiver.
Definitions of the different optimal receivers
$\text{Definition:}$ The maximum–a–posteriori–block-level receiver – for short: block–wise MAP – decides among the $2^k$ codewords $\underline{x}_i \in \mathcal{C}$ for the codeword with the highest a posteriori probability.
- \[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.03cm} \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \vert\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.\]
${\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}\vert \hspace{0.05cm} \underline{y} )$ is the conditional probability, that $\underline{x}_i$ was sent, when $\underline{y}$ is received.
We now try to simplify this decision rule step by step. The inference probability can be transformed according to the "Bayes rule" as follows:
- \[{\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}\vert \hspace{0.05cm} \underline{y} ) = \frac{{\rm Pr}( \underline{y} \hspace{0.08cm} |\hspace{0.05cm} \underline{x}_{\hspace{0.03cm}i} ) \cdot {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} )}{{\rm Pr}( \underline{y} )} \hspace{0.05cm}.\]
The probability ${\rm Pr}( \underline{y}) $ is independent of $\underline{x}_i$ and need not be considered in maximization. Moreover, if all $2^k$ information words $\underline{u}_i$ are equally probable, then the maximization can also dispense with the contribution ${\rm Pr}( \underline{x}_{\hspace{0.03cm}i} ) = 2^{-k}$ in the numerator.
$\text{Definition:}$ The probability ${\rm Pr}( \underline{y}) $ is independent of $\underline{x}_i$ and need not be considered in maximization. Moreover, if all $2^k$ information words $\underline{u}_i$ are equally probable, then the maximization can also dispense with the contribution ${\rm Pr}( \underline{x}_{\hspace{0.03cm}i} ) = 2^{-k}$ in the numerator.
- \[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} {\rm Pr}( \underline{y} \hspace{0.05cm}\vert\hspace{0.05cm} \underline{x}_{\hspace{0.03cm}i} ) \hspace{0.05cm}.\]
The conditional probability ${\rm Pr}( \underline{y} \hspace{0.05cm}\vert\hspace{0.05cm} \underline{x}_{\hspace{0.03cm}i} )$ is now to be understood in the forward direction, namely as the probability that the vector $\underline{y}$ is received when the codeword $\underline{x}_i$ has been sent.
In the following, we always use the maximum–likelihood–receiver at the block level. Due to the assumed equally likely information words, this also always provides the best possible decision
.
However, the situation is different on the bit level. The goal of an iterative decoding is just to estimate probabilities for all code bits $x_i \in \{0, 1\}$ and to pass these on to the next stage. For this one needs a MAP–receiver.
$\text{Definition:}$ The maximum–a–posteriori–bit-level receiver (short: bit–wise MAP) selects for each individual code bit $x_i$ the value $(0$ or $1)$ with the highest inference probability ${\rm Pr}( {x}_{\hspace{0.03cm}i}\vert \hspace{0.05cm} \underline{y} )$ from:
- \[\underline{z} = {\rm arg}\hspace{-0.1cm}{ \max_{ {x}_{\hspace{0.03cm}i} \hspace{0.03cm} \in \hspace{0.05cm} \{0, 1\} } \hspace{0.03cm} {\rm Pr}( {x}_{\hspace{0.03cm}i}\vert \hspace{0.05cm} \underline{y} ) \hspace{0.05cm} }.\]
Maximum likelihood decision at the BSC channel
We now apply the maximum–likelihood–criterion to the memoryless BSC–channel . Then holds:
- \[{\rm Pr}( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{x}_{\hspace{0.03cm}i} ) = \prod\limits_{l=1}^{n} {\rm Pr}( y_l \hspace{0.05cm}|\hspace{0.05cm} x_l ) \hspace{0.2cm}{\rm with}\hspace{0.2cm} {\rm Pr}( y_l \hspace{0.05cm}|\hspace{0.05cm} x_l ) = \left\{ \begin{array}{c} 1 - \varepsilon\\ \varepsilon \end{array} \right.\quad \begin{array}{*{1}c} {\rm if} \hspace{0.15cm} y_l = x_l \hspace{0.05cm},\\ {\rm if} \hspace{0.15cm}y_l \ne x_l\hspace{0.05cm}.\\ \end{array} \hspace{0.05cm}.\]
- \[\Rightarrow \hspace{0.3cm} {\rm Pr}( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{x}_{\hspace{0.03cm}i} ) = \varepsilon^{d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})} \cdot (1-\varepsilon)^{n-d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})} \hspace{0.05cm}.\]
$\text{Proof:}$ This result can be justified as follows:
- The Hamming–distance $d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})$ specifies the number of bit positions where the words $\underline{y}$ and $\underline{x}_{\hspace{0.03cm}i}$ differ with each $n$ binary element. Example: The Hamming–distance between $\underline{y}= (0, 1, 0, 1, 0, 1, 1)$ and $\underline{x}_{\hspace{0.03cm}i} = (0, 1, 0, 0, 1, 1)$ is $2$.
- In $n - d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})$ positions thus the two vectors $\underline{y}$ and $\underline{x}_{\hspace{0.03cm}i}$ do not differ. In the above example, five of the $n = 7$ bits are identical.
- Finally, one arrives at the above equation by substituting the falsification probability $\varepsilon$ or its complement $1-\varepsilon$.
The approach to maximum–likelihood–detection is to find the codeword $\underline{x}_{\hspace{0.03cm}i}$ that has the transition probability ${\rm Pr}( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{x}_{\hspace{0.03cm}i} )$ maximized:
- \[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} \left [ \varepsilon^{d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})} \cdot (1-\varepsilon)^{n-d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})} \right ] \hspace{0.05cm}.\]
Since the logarithm is a monotonically increasing function, the same result is obtained after the following maximization:
- \[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} L(\underline{x}_{\hspace{0.03cm}i})\hspace{0.5cm} {\rm with}\hspace{0.5cm} L(\underline{x}_{\hspace{0.03cm}i}) = \ln \left [ \varepsilon^{d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})} \cdot (1-\varepsilon)^{n-d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})} \right ] \]
- \[ \rightarrow \hspace{0.3cm} L(\underline{x}_{\hspace{0.03cm}i}) = d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i}) \cdot \ln \hspace{0.05cm} \varepsilon + \big [n -d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\big ] \cdot \ln \hspace{0.05cm} (1- \varepsilon) = \ln \frac{\varepsilon}{1-\varepsilon} \cdot d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i}) + n \cdot \ln \hspace{0.05cm} (1- \varepsilon) \hspace{0.05cm}.\]
Here we have to take into account:
- The second term of this equation is independent of $\underline{x}_{\hspace{0.03cm}i}$ and need not be considered further for maximization.
- Also, the factor before Hamming–distance is the same for all $\underline{x}_{\hspace{0.03cm}i}$ .
- Since $\ln \, {\varepsilon}/(1-\varepsilon)$ is negative (at least for $\varepsilon <0.5$, which can be assumed without much restriction), maximization becomes minimization, and the following final result is obtained:
$\text{Maximum–likelihood decision at the BSC channel.:}$
Choose from the $2^k$ allowed codewords $\underline{x}_{\hspace{0.03cm}i}$ the one with the least hamming–distance $d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})$ to the receiving vector $\underline{y}$ from:
- \[\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}, \hspace{0.2cm} \underline{y} \in {\rm GF}(2^n) \hspace{0.05cm}, \hspace{0.2cm}\underline{x}_{\hspace{0.03cm}i}\in {\rm GF}(2^n) \hspace{0.05cm}.\]
Applications of ML/BSC–decision can be found on the following pages:
- Single Parity–check Code (SPC)
Maximum likelihood decision at the AWGN channel
The AWGN–model for a $(n, k)$–block code differs from model on the first chapter page in that for $x$, $\tilde{x}$ and $y$ now the corresponding vectors $\underline{x}$, $\underline{\tilde{x}}$ and $\underline{y}$ must be used, each consisting of $n$ elements.
The steps to derive the maximum–likelihood–decider for AWGN are given below only in bullet form:
- The AWGN–channel is memoryless per se (the "White" in the name stands for this). Thus, for the conditional probability density function, it can be written:
- \[f( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{\tilde{x}} ) = \prod\limits_{l=1}^{n} f( y_l \hspace{0.05cm}|\hspace{0.05cm} \tilde{x}_l ) \hspace{0.05cm}.\]
- The conditional PDF is Gaussian for each individual code element $(l = 1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, n)$ . Thus, the entire PDF also satisfies a (one-dimensional) Gaussian distribution:
- \[f({y_l \hspace{0.03cm}| \hspace{0.03cm}\tilde{x}_l }) = \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot \exp \left [ - \frac {(y_l - \tilde{x}_l)^2}{2\sigma^2} \right ]\hspace{0.3cm} \Rightarrow \hspace{0.3cm} f( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{\tilde{x}} ) = \frac {1}{(2\pi)^{n/2} \cdot \sigma^n } \cdot \exp \left [ - \frac {1}{2\sigma^2} \cdot \sum_{l=1}^{n} \hspace{0.2cm}(y_l - \tilde{x}_l)^2 \right ] \hspace{0.05cm}.\]
- Since $\underline{y}$ is now value continuous rather than value discrete as in the BSC–model, probability densities must now be examined according to the ML–decision rule rather than probabilities. The optimal result is:
- \[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} f( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{\tilde{x}}_i )\hspace{0.05cm}, \hspace{0.5cm} \underline{y} \in R^n\hspace{0.05cm}, \hspace{0.2cm}\underline{x}_{\hspace{0.03cm}i}\in {\rm GF}(2^n) \hspace{0.05cm}.\]
- In algebra, the distance between two points $\underline{y}$ and $\underline{\tilde{x}}$ in $n$–dimensional space is called the Euclidiean distance, named after the Greek mathematician Euclid who lived in the third century BC:
- \[d_{\rm E}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{\tilde{x}}) = \sqrt{\sum_{l=1}^{n} \hspace{0.2cm}(y_l - \tilde{x}_l)^2}\hspace{0.05cm},\hspace{0.8cm} \underline{y} \in R^n\hspace{0.05cm}, \hspace{0.2cm}\underline{x}_{\hspace{0.03cm}i}\in \mathcal{C} \hspace{0.05cm}.\]
- Thus, the ML–decision rule at the AWGN–channel for any block code considering that the first factor of the WDF $f( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{\tilde{x}_i} )$ is constant:
- \[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} \exp \left [ - \frac {d_{\rm E}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{\tilde{x}}_i)}{2\sigma^2} \right ]\hspace{0.05cm}, \hspace{0.8cm} \underline{y} \in R^n\hspace{0.05cm}, \hspace{0.2cm}\underline{x}_{\hspace{0.03cm}i}\in {\rm GF}(2^n) \hspace{0.05cm}.\]
After a few more intermediate steps, you arrive at the result:
$\text{Maximum–likelihood decision at the AWGN channel:}$
Choose from the $2^k$ allowed codewords $\underline{x}_{\hspace{0.03cm}i}$ the one with the smallest Euclidean distance $d_{\rm E}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})$ to the receiving vector $\underline{y}$ from:
- \[\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} d_{\rm E}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}, \hspace{0.8cm} \underline{y} \in R^n\hspace{0.05cm}, \hspace{0.2cm}\underline{x}_{\hspace{0.03cm}i}\in {\rm GF}(2^n) \hspace{0.05cm}.\]
Exercises for the chapter
Exercise 1.3: Channel Models BSC - BEC - BSEC - AWGN
Exercise 1.4: Maximum Likelihood Decision