Difference between revisions of "Channel Coding/The Basics of Turbo Codes"
| Line 116: | Line 116: | ||
== Symbol-wise iterative decoding of a turbo code == | == Symbol-wise iterative decoding of a turbo code == | ||
<br> | <br> | ||
| − | + | The decoding of a turbo code is basically done as described in section [[Channel_Coding/Soft-in_Soft-Out_Decoder#Symbol-wise_soft-in_soft-out_decoding|"Symbol-wise Soft–in Soft–out Decoding"]] . From the following graphic, however, you can also see some special features that apply only to the turbo decoder.<br> | |
| − | [[File:P ID3049 KC T 4 3 S4a v2.png|center|frame| | + | [[File:P ID3049 KC T 4 3 S4a v2.png|center|frame|Iterative turbo decoder for rate $R = 1/3$|class=fit]] |
| − | + | Assumed is a rate ;$1/3$ turbo code according to the description on the [[The_Basics_of_Turbo_Codes#Basic_structure_of_a_turbo_code| "first page of this section"]]. Also, the color scheme for the information sequence $\underline{u}$ and the two parity sequences $\underline{p}_1$ and $\underline{p}_2$ are adapted from the earlier graphics. Further, it should be noted: | |
| − | |||
| − | * | + | *The received vectors $\underline{y}_0, \underline{y}_1$ and $\underline{y}_2$ are real-valued and provide the respective soft information with respect to the information sequence $\underline{u}$ and the sequences $\underline{p}_1$ (parity for encoder 1) and $\underline{p}_2$ (parity for encoder 2).<br> |
| − | * | + | *The decoder 1 receives the required intrinsic information in the form of the $L$ values $L_{\rm K,\hspace{0.03cm} 0}$ $($out $\underline{y}_0)$ and $L_{\rm K,\hspace{0. 03cm}1}$ $($out $\underline{y}_1)$ over each bit of the sequences $\underline{u}$ and $\underline{p}_1$. In the second decoder, the scrambling of the information sequence $\underline{u}$ must be taken into account. Thus, the $L$ values to be processed are $\pi(L_{\rm K, \hspace{0.03cm}0})$ and $L_{\rm K, \hspace{0.03cm}2}$.<br> |
| + | |||
| + | *In general [[Channel_Coding/Soft-in_Soft-Out_Decoder#Basic_structure_of_concatenated_coding_systems|"SISO decoder"]] the information exchange between the two component decoders was controlled with $\underline{L}_{\rm A, \hspace{0. 03cm}2} = \underline{L}_{\rm E, \hspace{0.03cm}1}$ and $\underline{L}_{\rm A, \hspace{0.03cm}1} = \underline{L}_{\rm E, \hspace{0.03cm}2}$ . Written out at the bit level, these equations are denoted by $1 ≤ i ≤ n$: | ||
::<math>L_{\rm A, \hspace{0.03cm}2}(i) = L_{\rm E, \hspace{0.03cm}1}(i) | ::<math>L_{\rm A, \hspace{0.03cm}2}(i) = L_{\rm E, \hspace{0.03cm}1}(i) | ||
| Line 131: | Line 132: | ||
L_{\rm A, \hspace{0.03cm}1}(i) = L_{\rm E, \hspace{0.03cm}2}(i) \hspace{0.03cm}.</math> | L_{\rm A, \hspace{0.03cm}1}(i) = L_{\rm E, \hspace{0.03cm}2}(i) \hspace{0.03cm}.</math> | ||
| − | * | + | *In the case of the turbo decoder, the interleaver must also be taken into account in this information exchange. Then for $i = 1, \ \text{...}\hspace{0.05cm} , \ n$: |
::<math>L_{\rm A, \hspace{0.03cm}2}\left ({\rm \pi}(i) \right ) = L_{\rm E, \hspace{0.03cm}1}(i) | ::<math>L_{\rm A, \hspace{0.03cm}2}\left ({\rm \pi}(i) \right ) = L_{\rm E, \hspace{0.03cm}1}(i) | ||
| Line 137: | Line 138: | ||
L_{\rm A, \hspace{0.03cm}1}(i) = L_{\rm E, \hspace{0.03cm}2}\left ({\rm \pi}(i) \right ) \hspace{0.05cm}.</math> | L_{\rm A, \hspace{0.03cm}1}(i) = L_{\rm E, \hspace{0.03cm}2}\left ({\rm \pi}(i) \right ) \hspace{0.05cm}.</math> | ||
| − | * | + | *The a posteriori $L$ value is (arbitrarily) given by decoder 1 in the above model. This can be justified by the fact that one iteration stands for a twofold information exchange.<br> |
| − | == | + | == Performance of the turbo codes == |
<br> | <br> | ||
| − | [[File:P ID3053 KC T 4 3 S5a v7.png|right|frame| | + | [[File:P ID3053 KC T 4 3 S5a v7.png|right|frame|Bit and block error probability of turbo codes at AWGN–channel.]] |
| − | + | We consider, as in the last pages, the rate $1/$3 turbo code. | |
| − | * | + | *with equal filter functions $G_1(D) = G_2(D) = (1 + D^2)/(1 + D + D^2)$ ⇒ Memory $m = 2$,<br> |
| − | * | + | *with the interleaver variable $K$; first apply $K = 10000,$<br> |
| − | * | + | *a sufficient number of iterations $(I = 20)$, almost equivalent in result to "$I → ∞$".<br><br> |
| − | + | The two RSC component codes are each terminated on $K$ bits. Therefore we group | |
| − | * | + | * the information sequence $\underline{u}$ into blocks of $K$ information bits each, and<br> |
| − | * | + | *the code sequence $\underline{x}$ to blocks with each $N = 3 \cdot K$ code bits.<br><br> |
| − | + | All results apply to the [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_binary_input|"AWGN channel"]]. Data taken from lecture notes [Liv15]<ref>Liva, G.: ''Channels Codes for Iterative Decoding.'' Lecture notes, Department of Communications Engineering, TU Munich and DLR Oberpfaffenhofen, 2015.</ref>. | |
| − | + | The graph shows as a green curve the '''block error probability'''' ⇒ ${\rm Pr(block error)}$ in double logarithmic representation depending on the AWGN characteristic $10 \cdot {\rm lg} \, (E_{\rm B}/N_0)$. It can be seen: | |
*Die mit Kreuzen markierten Punkte ergaben sich aus den Gewichtsfunktionen des Turbocodes mit Hilfe der [[Channel_Coding/Schranken_f%C3%BCr_die_Blockfehlerwahrscheinlichkeit#Union_Bound_der_Blockfehlerwahrscheinlichkeit| "Union Bound"]]. Die Simulationsergebnisse – in der Grafik durch Kreise markiert – sind nahezu deckungsgleich mit den analytisch berechneten Werten.<br> | *Die mit Kreuzen markierten Punkte ergaben sich aus den Gewichtsfunktionen des Turbocodes mit Hilfe der [[Channel_Coding/Schranken_f%C3%BCr_die_Blockfehlerwahrscheinlichkeit#Union_Bound_der_Blockfehlerwahrscheinlichkeit| "Union Bound"]]. Die Simulationsergebnisse – in der Grafik durch Kreise markiert – sind nahezu deckungsgleich mit den analytisch berechneten Werten.<br> | ||
Revision as of 23:18, 14 November 2022
Contents
- 1 Basic structure of a turbo code
- 2 Further modification of the basic structure of the turbo code
- 3 First requirement for turbo codes: Recursive component codes
- 4 Second requirement for turbo codes: Interleaving
- 5 Symbol-wise iterative decoding of a turbo code
- 6 Performance of the turbo codes
- 7 Seriell verkettete Turbocodes – SCCC
- 8 Einige Anwendungsgebiete für Turbocodes
- 9 Aufgaben zum Kapitel
- 10 Quellenverzeichnis
Basic structure of a turbo code
All communications systems current today (2017), such as "UMTS" (Universal Mobile Telecommunications System ⇒ 3rd generation mobile communications) and "LTE" (Long Term Evolution ⇒ 4th generation mobile communications) use the concept of "symbol-wise iterative decoding". That this is so is directly related to the invention of turbo codes' in 1993 by "Claude Berrou", "Alain Glavieux" and "Punya Thitimajshima" because it was only with these codes that the Shannon bound could be approached with reasonable decoding effort.
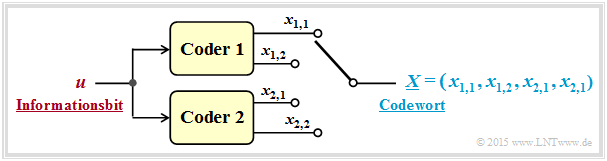
Turbo codes result from the parallel or serial concatenation of convolutional codes. The graphic shows the parallel concatenation of two codes, each with the parameters $k = 1, \ n = 2$ ⇒ Rate $R = 1/2$.
In this representation:
- $u$ the currently considered bit of the information sequence $\underline{u}$,
- $x_{i,\hspace{0.03cm}j}$ the currently considered bit at the output $j$ of encoder $i$ $($with $1 ≤ i ≤ 2, \ 1 ≤ j ≤ 2)$,
- $\underline{X} = (x_{1,\hspace{0.03cm}1}, \ x_{1,\hspace{0.03cm}2}, \ x_{2,\hspace{0.03cm}1}, \ x_{2,\hspace{0.03cm}2})$ the code word for the current information bit $u$.
The resulting rate of the concatenated coding system is thus $R = 1/4$.
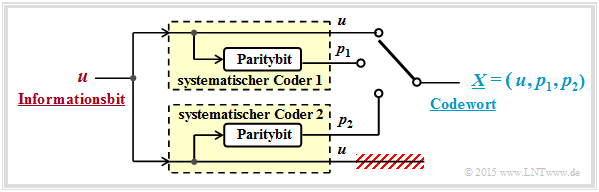
If systematic component codes are used, the following model results:
The modifications from the top graph can be justified as follows:
- For systematic codes $C_1$ and $C_2$ both $x_{1,\hspace{0.03cm}1} = u$ and $x_{2,\hspace{0.03cm}1} = u$. Therefore, one can dispense with the transmission of a redundant bit $($for example $x_{2,\hspace{0.03cm}2})$ .
- With this reduction, the result is a rate–$1/3$–turbo code with $k = 1$ and $n = 3$. The code word with the parity bits is $p_1$ (encoder 1) and $p_2$ (encoder 2):
- $$\underline{X} = \left (u, \ p_1, \ p_2 \right )\hspace{0.05cm}.$$
Further modification of the basic structure of the turbo code
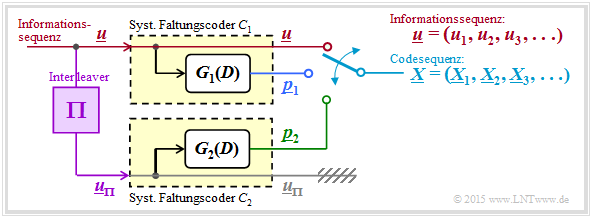
In the following we always assume a still somewhat further modified turbo encoder model:
- As required for the description of convolutional codes, now at the input instead of the isolated information bit $u$ the information sequence $\underline{u} = (u_1, \ u_2, \ \text{...}\hspace{0.05cm} , \ u_i , \ \text{...}\hspace{0.05cm} )$ an.
- The code word sequence is generated with $\underline{x} = (\underline{X}_1, \underline{X}_2, \ \text{...}\hspace{0.05cm} , \ \underline{X}_i, \ \text{...}\hspace{0.05cm} )$ denoted. To avoid confusion, the code words $\underline{X}_i = (u, \ p_1, \ p_2)$ with capital letters were introduced in front.
- The encoders $\mathcal{C}_1$ and $\mathcal{C}_2$ are conceived (at least in thought) as "digital filters" and are thus characterized by the "transfer functions" $G_1(D)$ and $G_2(D)$ representable.
- For various reasons ⇒ see "two pages ahead" the input sequence of the second encoder ⇒ $\underline{u}_{\pi}$ should be scrambled with respect to the sequence $\underline{u}$ by an interleaver $(\Pi)$ .
- Thereby there is nothing against choosing both encoders the same: $G_1(D) = G_2(D) = G(D)$. Without interleaver the correction capability would be extremely limited.
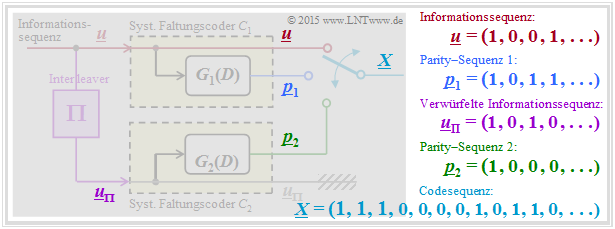
$\text{Example 1:}$ The graph shows the different sequences in matched colors. To note:
- For $\underline{u}_{\pi}$ a $3×4$–interleaver matrix is considered according to "Exercise 4.8Z" .
- The parity sequences are obtained according to $G_1(D) = G_2(D) = 1 + D^2$ ⇒ see "Exercise 4.8".
First requirement for turbo codes: Recursive component codes
Non-recursive transfer functions for generating the parity sequences cause a turbo code with insufficiently small minimum distance. The reason for this inadequacy is the finite impulse response $\underline{g} = (1, \ g_2, \ \text{...}\hspace{0.05cm} , \ g_m, \ 0, \ 0, \ \text{...}\hspace{0.05cm} )$ with $g_2, \ \text{...}\hspace{0.05cm} , \ g_m ∈ \{0, 1\}$. Here $m$ denotes the code memory.
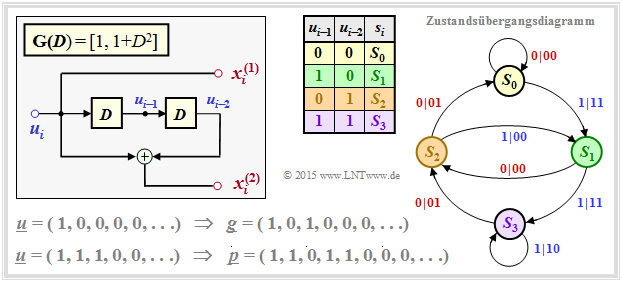
The graph shows the state transition diagram for the example $\mathbf{G}(D) = \big [1, \ 1 + D^2 \big ]$. The transitions are labeled "$u_i\hspace{0.05cm}|\hspace{0.05cm}u_i p_i$".
- The sequence $S_0 → S_1 → S_2 → S_0 → S_0 → \ \text{...}\hspace{0.05cm} \ $ with respect to the input, leads to the information sequence $\underline{u} = (1, 0, 0, 0, 0, \ \text{...}\hspace{0.05cm})$
- and with respect to the respective second code symbol to the parity sequence $\underline{p} = (1, 0, 1, 0, 0, \ \text{...}\hspace{0.05cm})$ ⇒ identical to the impulse response $\underline{g}$ ⇒ memory $m = 2$.
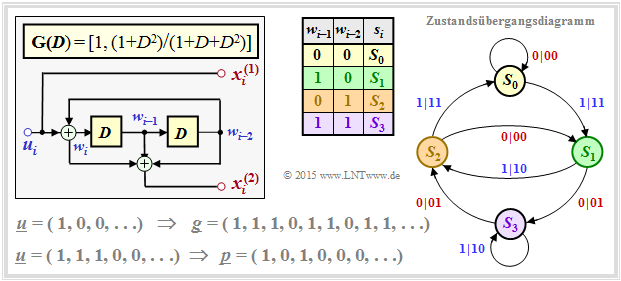
The lower graph applies to a so-called RSC code (Recursive Systematic Convolutional) correspondingly $\mathbf{G}(D) = \big [1, \ (1+ D^2)/(1 + D + D^2)\big ]$.
- Here the sequence $S_0 → S_1 → S_3 → S_2 → S_1 → S_3 → S_2 → \ \text{...}\hspace{0.05cm} \ $ to the impulse response $\underline{g} = (1, 1, 1, 0, 1, 1, 0, 1, 1, \ \text{...}\hspace{0.05cm})$.
- This impulse response continues to infinity due to the loop $S_1 → S_3 → S_2 → S_1$. This enables or facilitates the iterative decoding.
More details on the examples on this page can be found in the "Exercise 4.8" and the "Exercise 4.9".
Second requirement for turbo codes: Interleaving
It is obvious that for $G_1(D) = G_2(D)$ an interleaver $(\Pi)$ is essential. Another reason is that the apriori information is assumed to be independent. Thus, adjacent (and thus possibly strongly dependent) bits for the other subcode should be far apart.
Indeed, for any RSC code ⇒ infinite impulse response $\underline{g}$ ⇒ fractional–rational transfer function $G(D)$ there are certain input sequences $\underline{u}$, which lead to very short parity sequences $\underline{p} = \underline{u} ∗ \underline{g}$ with low Hamming weight $w_{\rm H}(\underline{p})$ .
For example, such a sequence is given in the graphic below on the "last page" : $\underline{u} = (1, 1, 1, 0, 0, \ \text{...}\hspace{0.05cm})$. Then for the output sequence holds:
- \[P(D) = U(D) \cdot G(D) = (1+D+D^2) \cdot \frac{1+D^2}{1+D+D^2}= 1+D^2\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \underline{p}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm}\hspace{0.05cm})\hspace{0.05cm}. \]
$\text{Meaning and purpose:}$ By $\rm interleaving$, it is now ensured with high probability that this sequence $\underline{u} = (1, 1, 1, 0, 0, \ \text{...}\hspace{0.05cm})$ is converted into a sequence $\underline{u}_{\pi}$ ,
- which also contains only three ones,
- but whose output sequence is characterized by a large Hamming weight $w_{\rm H}(\underline{p})$ .
Thus, the decoder succeeds in resolving such "problem sequences" iteratively.
For the following description of the interleavers we use the assignment $I_{\rm In} → I_{\rm Out}$. These labels stand for the indices of output and input sequence, respectively. The interleaver variable is named $I_{\rm max}$ .
There are several, fundamentally different interleaver concepts:
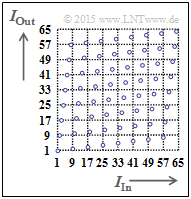
In a block interleaver one fills a matrix with $S$ columns and $Z$ rows column by column and reads the matrix row by row. Thus an information block with $I_{\rm max} = S \cdot Z$ bit is deterministically scrambled.
The right graph illustrates the principle for $I_{\rm max} = 64$ ⇒ $1 ≤ I_{\rm In} \le 64$ $1 ≤ I_{\rm Out} \le 64$. The order of the output bits is then: $1, 9, 17, 25, 33, 41, 49, 57, 2, 10, 18, \ \text{...}\hspace{0.05cm} , 48, 56, 64.$
More information on block interleaving is available in the "Exercise 4.8Z".
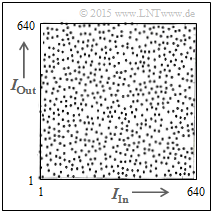
Turbo codes often use the $S$–random interleaver. This pseudo random algorithm with the parameter "$S$" guarantees that two indices less than $S$ apart at the input occur at least at the distance $S + 1$ at the output. The left graph shows the $S$–random characteristic $I_{\rm Out}(I_{\rm In})$ for $I_{\rm max} = 640$.
- This algorithm is also deterministic, and one can undo the scrambling in the decoder ⇒ De–interleaving.
- The distribution still seems more "random" than with block interleaving.
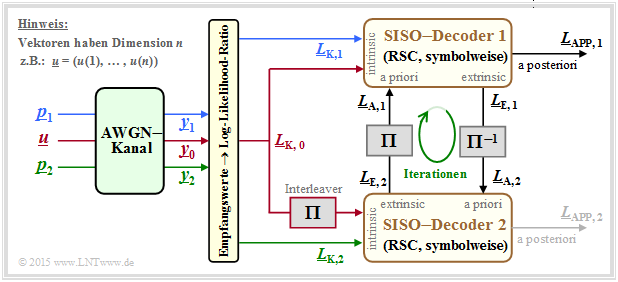
Symbol-wise iterative decoding of a turbo code
The decoding of a turbo code is basically done as described in section "Symbol-wise Soft–in Soft–out Decoding" . From the following graphic, however, you can also see some special features that apply only to the turbo decoder.
Assumed is a rate ;$1/3$ turbo code according to the description on the "first page of this section". Also, the color scheme for the information sequence $\underline{u}$ and the two parity sequences $\underline{p}_1$ and $\underline{p}_2$ are adapted from the earlier graphics. Further, it should be noted:
- The received vectors $\underline{y}_0, \underline{y}_1$ and $\underline{y}_2$ are real-valued and provide the respective soft information with respect to the information sequence $\underline{u}$ and the sequences $\underline{p}_1$ (parity for encoder 1) and $\underline{p}_2$ (parity for encoder 2).
- The decoder 1 receives the required intrinsic information in the form of the $L$ values $L_{\rm K,\hspace{0.03cm} 0}$ $($out $\underline{y}_0)$ and $L_{\rm K,\hspace{0. 03cm}1}$ $($out $\underline{y}_1)$ over each bit of the sequences $\underline{u}$ and $\underline{p}_1$. In the second decoder, the scrambling of the information sequence $\underline{u}$ must be taken into account. Thus, the $L$ values to be processed are $\pi(L_{\rm K, \hspace{0.03cm}0})$ and $L_{\rm K, \hspace{0.03cm}2}$.
- In general "SISO decoder" the information exchange between the two component decoders was controlled with $\underline{L}_{\rm A, \hspace{0. 03cm}2} = \underline{L}_{\rm E, \hspace{0.03cm}1}$ and $\underline{L}_{\rm A, \hspace{0.03cm}1} = \underline{L}_{\rm E, \hspace{0.03cm}2}$ . Written out at the bit level, these equations are denoted by $1 ≤ i ≤ n$:
- \[L_{\rm A, \hspace{0.03cm}2}(i) = L_{\rm E, \hspace{0.03cm}1}(i) \hspace{0.5cm}{\rm bzw.}\hspace{0.5cm} L_{\rm A, \hspace{0.03cm}1}(i) = L_{\rm E, \hspace{0.03cm}2}(i) \hspace{0.03cm}.\]
- In the case of the turbo decoder, the interleaver must also be taken into account in this information exchange. Then for $i = 1, \ \text{...}\hspace{0.05cm} , \ n$:
- \[L_{\rm A, \hspace{0.03cm}2}\left ({\rm \pi}(i) \right ) = L_{\rm E, \hspace{0.03cm}1}(i) \hspace{0.5cm}{\rm bzw.}\hspace{0.5cm} L_{\rm A, \hspace{0.03cm}1}(i) = L_{\rm E, \hspace{0.03cm}2}\left ({\rm \pi}(i) \right ) \hspace{0.05cm}.\]
- The a posteriori $L$ value is (arbitrarily) given by decoder 1 in the above model. This can be justified by the fact that one iteration stands for a twofold information exchange.
Performance of the turbo codes
We consider, as in the last pages, the rate $1/$3 turbo code.
- with equal filter functions $G_1(D) = G_2(D) = (1 + D^2)/(1 + D + D^2)$ ⇒ Memory $m = 2$,
- with the interleaver variable $K$; first apply $K = 10000,$
- a sufficient number of iterations $(I = 20)$, almost equivalent in result to "$I → ∞$".
The two RSC component codes are each terminated on $K$ bits. Therefore we group
- the information sequence $\underline{u}$ into blocks of $K$ information bits each, and
- the code sequence $\underline{x}$ to blocks with each $N = 3 \cdot K$ code bits.
All results apply to the "AWGN channel". Data taken from lecture notes [Liv15][1].
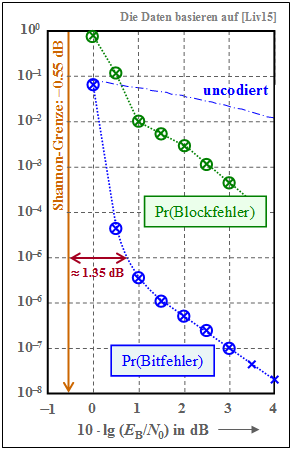
The graph shows as a green curve the block error probability' ⇒ ${\rm Pr(block error)}$ in double logarithmic representation depending on the AWGN characteristic $10 \cdot {\rm lg} \, (E_{\rm B}/N_0)$. It can be seen:
- Die mit Kreuzen markierten Punkte ergaben sich aus den Gewichtsfunktionen des Turbocodes mit Hilfe der "Union Bound". Die Simulationsergebnisse – in der Grafik durch Kreise markiert – sind nahezu deckungsgleich mit den analytisch berechneten Werten.
- Die "Union Bound" ist nur eine obere Schranke, basierend auf Maximum–Likelihood–Decodierung ("ML"). Der iterative Decoder ist suboptimal (also schlecher als "ML"). Diese beiden Effekte heben sich scheinbar nahezu auf.
- Etwa bei $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) = 1 \ \rm dB$ ist ein Knick im (grünen) Kurvenverlauf festzustellen, der mit der Steigungsänderung von ${\rm Pr(Bitfehler)}$ ⇒ blaue Kurve korrespondiert.
Die blauen Kreuze (Berechnung) und die blauen Kreise (Simulation) bezeichnen die Bitfehlerwahrscheinlichkeit für die Interleavergröße $K = 10000$ . Als Vergleichskurve eingezeichnet ist die (strichpunktierte) Kurve für uncodierte Übertragung. Zu diesen blauen Kurven ist anzumerken:
- Bei kleinen Abszissenwerten ist der Kurvenabfall in der gewählten Darstellung nahezu linear und ausreichend steil. Zum Beispiel benötigt man für ${\rm Pr(Bitfehler)} = 10^{-5}$ mindestens $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx \, 0.8 \ \rm dB$.
- Im Vergleich zur Shannon–Grenze, die sich für die Coderate $R = 1/3$ zu $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx \, –0.55 \ \rm dB$ ergibt, liegt unser Standard–Turbocode $($mit Gedächtnis $m = 2)$ nur etwa $1.35 \ \rm dB$ entfernt.
- Ab $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx 0.5 \ \rm dB$ verläuft die Kurve flacher. Ab ca. $1.5 \ \rm dB$ ist der Verlauf wieder (nahezu) linear mit geringerer Steigung. Für ${\rm Pr(Bitfehler)} = 10^{-7}$ benötigt man etwa $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) = 3 \ \rm dB$.
Wir versuchen nun, den flacheren Abfall der Bitfehlerwahrscheinlichkeit bei größerem $E_{\rm B}/N_0$ zu erklären. Man spricht von einem $\text{Error Floor}$:
- Der Grund für dieses asymptotisch schlechtere Verhalten bei besserem Kanal $($im Beispiel: ab $10 \cdot {\rm lg} \, E_{\rm B}/N_0 \approx 2 \ \rm dB)$ ist die Periode $P$ der Coderimpulsantwort $\underline{g}$, wie auf der Seite Interleaving nachgewiesen und in der Aufgabe 4.10 an Beispielen erläutert.
- Für $m = 2$ ist die Periode $P = 2^m -1 = 3$. Dadurch ist für $\underline{u} = (1, 1, 1) ⇒ w_{\rm H}(\underline{u}) = 3$ trotz unbegrenzter Impulsantwort $\underline{g}$ die Paritysequenz begrenzt: $\underline{p} = (1, 0, 1)$ ⇒ $w_{\rm H}(\underline{p}) = 2$.
- Die Sequenz $\underline{u} = (0, \ \text{...}\hspace{0.05cm} , \ 0, \ 1, \ 0, \ 0, \ 1, \ 0, \ \text{...}\hspace{0.05cm})$ ⇒ $U(D) = D^x \cdot (1 + D^P)$ führt ebenfalls zu einem kleinen Hamming–Gewicht $w_{\rm H}(\underline{p})$ am Ausgang, was den iterativen Decodierprozess erschwert.
- Eine gewisse Abhilfe schafft der Interleaver, der dafür sorgt, dass nicht die beiden Sequenzen $\underline{p}_1$ und $\underline{p}_2$ gleichzeitig durch sehr kleine Hamming–Gewichte $w_{\rm H}(\underline{p}_1)$ und $w_{\rm H}(\underline{p}_2)$ belastet sind.
- Aus der Grafik erkennt man auch, dass die Bitfehlerwahrscheinlichkeit umgekehrt proportional zur Interleavergröße $K$ ist. Das heißt: Bei großem $K$ funktioniert die Entspreizung ungünstiger Eingangssequenzen besser.
- Allerdings gilt die Näherung $K \cdot {\rm Pr(Bitfehler) = const.}$ nur für größere $E_{\rm B}/N_0$–Werte ⇒ kleine Bitfehlerwahrscheinlichkeiten. Der beschriebene Effekt tritt zwar auch bei kleinerem $E_{\rm B}/N_0$ auf, doch sind dann die Auswirkungen auf die Bitfehlerwahrscheinlichkeit geringer.
Dagegen gilt der flachere Verlauf der Blockfehlerwahrscheinlichkeit (grüne Kurve) weitgehend unabhängig von der Interleavergröße $K$, also sowohl für $K = 1000$ als auch für $K = 10000$. Im Bereich ab $10 \cdot {\rm lg} \, E_{\rm B}/N_0 > 2 \ \rm dB$ dominieren nämlich Einzelfehler, so dass hier die Näherung ${\rm Pr(Blockfehler)} \approx {\rm Pr(Bitfehler)} \cdot K$ gültig ist.
$\text{Fazit:}$ Die beispielhaft gezeigten Kurven für Bitfehlerwahrscheinlichkeit und Blockfehlerwahrscheinlichkeit gelten qualitativ auch für $m > 2$, zum Beispiel für den Turbocode von UMTS und LTE $($jeweils mit $m = 3)$, der in der Aufgabe 4.10 analysiert wird. Es ergeben sich aber einige quantitative Unterschiede:
- Die Kurve verläuft bei kleinem $E_{\rm B}/N_0$ steiler und der Abstand von der Shannongrenze ist etwas geringer als im hier gezeigten Beispiel für $m = 2$.
- Auch für größeres $m$ gibt es einen Error Floor. Der Knick in den dargestellten Kurven erfolgt dann aber später, also bei kleineren Fehlerwahrscheinlichkeiten.
Seriell verkettete Turbocodes – SCCC
Die bisher betrachteten Turbocodes werden manchmal auch als Parallel Concatenated Convolutional Codes (PCCC) bezeichnet.
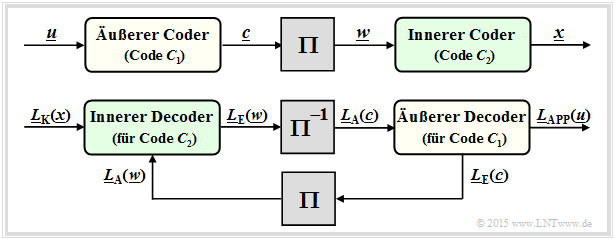
Einige Jahre nach Berrou's Erfindung wurden von anderen Autoren auch Serial Concatenated Convolutional Codes (SCCC) entsprechend der folgenden Grafik vorgeschlagen.
- Die Informationssequenz $\underline{u}$ liegt am äußeren Faltungscoder $\mathcal{C}_1$ an. Dessen Ausgangssequenz sei $\underline{c}$.
- Nach dem Interleaver $(\Pi)$ folgt der innere Faltungscoder $\mathcal{C}_2$. Die Codesequenz wird hier $\underline{x}$ genannt.
- Die resultierende Coderate ist $R = R_1 \cdot R_2$. Bei Rate–$1/2$–Komponentencodes ist $R = 1/4$.
Die untere Grafik zeigt den SCCC–Decoder und verdeutlicht die Verarbeitung der $L$–Werte und den Austausch der extrinsischen Information zwischen den beiden Komponentencoder:
- Der innere Decoder (für den Code $\mathcal{C}_2)$ erhält vom Kanal die intrinsische Information $\underline{L}_{\rm K}(\underline{x})$ und vom äußeren Decoder (nach Interleaving) die Apriori–Information $\underline{L}_{\rm A}(\underline{w})$ mit $\underline{w} = \pi(\underline{c})$. An den äußeren Decoder wird die extrinsische Information $\underline{L}_{\rm E}(\underline{w})$ abgegeben.
- Der äußere Decoder $($für $\mathcal{C}_1)$ verarbeitet die Apriori–Information $\underline{L}_{\rm A}(\underline{c})$, also die extrinsische Information $\underline{L}_{\rm E}(\underline{w})$ nach dem De–Interleaving. Er liefert die extrinsische Information $\underline{L}_{\rm E}(\underline{c})$.
- Nach hinreichend vielen Iterationen ergibt sich das das gewünschte Decodierergebnis in Form der Aposteriori–$L$–Werte $\underline{L}_{\rm APP}(\underline{u})$ der Informationssequenz $\underline{u}$.
$\text{Fazit:}$ Wichtig für Serial Concatenated Convolutional Codes (SCCC) ist, dass der innere Code $\mathcal{C}_2$ rekursiv ist (also ein RSC–Code). Der äußere Code $\mathcal{C}_1$ kann auch nichtrekursiv sein.
Zur Leistungsfähigkeit solcher Codes ist anzumerken:
- Ein SCCC ist bei großem $E_{\rm B}/N_0$ oft besser als ein PCCC ⇒ niedrigerer Error Floor. Die Aussage gilt schon für SCCC–Komponentencodes mit Gedächtnis $m = 2$ (nur vier Trelliszustände), während bei PCCC das Gedächtnis $m = 3$ bzw. $m = 4$ (acht bzw. sechzehn Trelliszustände) sein sollte.
- Im unteren Bereich $($kleines $E_{\rm B}/N_0)$ ist dagegen der beste seriell verkettete Faltungscode (SCCC) um einige Zehntel Dezibel schlechter als der vergleichbare Turbocode gemäß Berrou (PCCC). Entsprechend größer ist auch der Abstand von der Shannongrenze.
Einige Anwendungsgebiete für Turbocodes
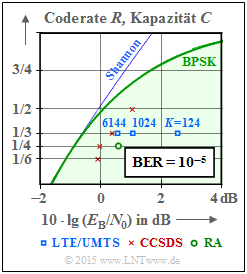
In fast allen neueren Kommunikationssystemen werden Turbocodes eingesetzt. Die Grafik zeigt deren Leistungsfähigkeit beim AWGN–Kanal im Vergleich zur Shannonschen Kanalkapazität (blaue Kurve).
Der grün hinterlegte Bereich "BPSK" gibt die Shannongrenze für Nachrichtensysteme mit binärem Eingang an, mit der nach dem Kanalcodierungstheorem eine fehlerfreie Übertragung gerade noch möglich ist.
Anzumerken ist, dass hier für die eingezeichneten Kanalcodes von standardisierten Systemen die Fehlerrate $10^{-5}$ zugrunde liegt, während die informationstheoretischen Kapazitätskurven (Shannon, BPSK) für die Fehlerwahrscheinlichkeit $0$ gelten.
- Die blauen Rechtecke markieren die Turbocodes für UMTS. Diese sind Rate–$1/3$–Codes mit Gedächtnis $m = 3$. Die Leistungsfähigkeit hängt stark von der Interleavergröße ab. Mit $K = 6144$ liegt dieser Code nur etwa $1 \ \rm dB$ rechts von der Shannon–Grenze. LTE verwendet die gleichen Turbocodes. Geringfügige Unterschiede ergeben sich aufgrund des unterschiedlichen Interleavers.
- Die roten Kreuze markieren die Turbocodes nach CCSDS (Consultative Comittee for Space Data Systems), entwickelt für den Einsatz bei Weltraummissionen. Diese Klasse geht von der festen Interleavergröße $K = 6920$ aus und stellt Codes der Rate $1/6$, $1/4$, $1/3$ und $1/2$ bereit. Die niedrigsten Coderaten erlauben einen Betrieb mit $10 \cdot {\rm lg} \, (E_{\rm B}/N_0) \approx 0 \ \rm dB$.
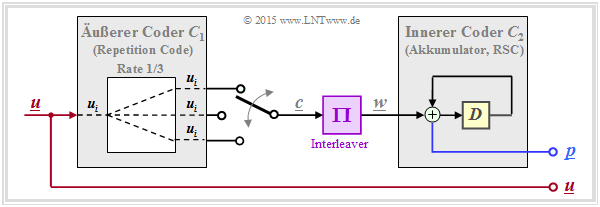
- Der grüne Kreis steht für einen sehr einfachen Repeat–Accumulate (RA) Code, einem seriell–verketteten Turbocode. Nachfolgend ist dessen Struktur skizziert: Der äußere Decoder verwendet einen Wiederholungscode (englisch: Repetition Code), im gezeichneten Beispiel mit der Rate $R = 1/3$. Nach dem Interleaver folgt ein RSC–Code mit $G(D) = 1/(1 + D)$ ⇒ Gedächtnis $m = 1$. Bei systematischer Ausführung ist die Gesamtcoderate $R = 1/4$ (zu jedem Informationsbit werden noch drei Paritybit hinzugefügt).
Aus der Grafik rechts oben erkennt man, dass dieser einfache RA–Code überraschend gut ist. Mit der Interleavergröße $K = 300000$ beträgt der Abstand von der Shannon–Grenze lediglich etwa $1.5 \ \rm dB$ (grüner Punkt).
Ähnliche Repeat Accumulate Codes sind für den Standard DVB Return Channel Terrestrial (RCS) sowie für den WiMax–Standard (IEEE 802.16) vorgesehen.
Aufgaben zum Kapitel
Aufgabe 4.8: Wiederholung zu den Faltungscodes
Aufgabe 4.8Z: Grundlegendes zum Interleaving
Aufgabe 4.9: Recursive Systematic Convolutional Codes
Aufgabe 4.10: Turbocoder für UMTS und LTE
Quellenverzeichnis
- ↑ Liva, G.: Channels Codes for Iterative Decoding. Lecture notes, Department of Communications Engineering, TU Munich and DLR Oberpfaffenhofen, 2015.