Exercise 4.08Z: Basics about Interleaving
Interleaving is required, for example, for a channel with burst error characteristics in order to distribute the errors within the burst over a sufficiently large area so that they can subsequently be largely corrected $($or at least detected$)$.
For turbo codes based on so-called RSC encoder $($"Recursive Systematic Convolutional Encoder"$)$ – and only such make sense – interleaving is essential also with the AWGN channel, because then there are also always $($some$)$ input sequences, which deliver only "zeros" in the output sequence after quite a few "ones", and that to infinity ⇒ there are output sequences with very small Hamming weight.
If the bits of such input sequences are distributed over a wide range in the second encoder, the problem can be largely eliminated by the interaction of both component decoders in the case of iterative symbol-wise decoding.
A general distinction is made between
- block interleaver and
- random interleaver.
In block interleaving one fills a matrix with $N_{\rm C}$ columns and $N_{\rm R}$ rows column-by-column and reads the matrix row-by-row. This deterministically scrambles a block of information with $I_{\rm max} = N_{\rm C} \cdot N_{\rm R}$ bits.
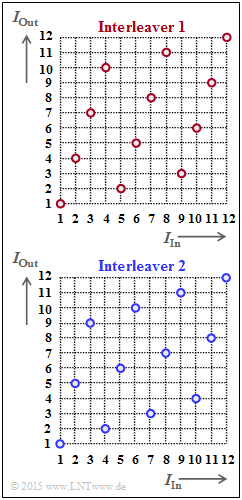
On the right, two interleavers are indicated and in graphical form by the assignment $I_{\rm Out}(I_{\rm In})$. These quantities represent the "output sequence index" and the "input sequence index", respectively. It holds:
- $$1 \le I_{\rm Out} \le I_{\rm max} \hspace{0.05cm},$$
- $$1 \le I_{\rm In} \le I_{\rm max} \hspace{0.05cm}. $$
In the subtask (1) it is asked whether this is "block interleaving" or "random interleaving". The latter are discussed in the "theory section" but only very briefly.
Hints:
- The exercise refers to the chapter "Basics of Turbo Codes".
- But other $\rm LNTwww$ books also discuss interleaving, including the book "Examples of Communication Systems" with reference to the
- standard digital subscriber line $\rm (DSL)$ ⇒ "Interleaving and Deinterleaving",
- 2G mobile communication system $\rm GSM$ ⇒ "Components of voice and data transmission",
- 3G mobile communication system $\rm UMTS$ ⇒ "Channel Coding",
- 4G mobile communication system $\rm LTE$ ⇒ "Functionality of SC-FDMA" $($in the boo "Mobile Communications"$)$.
Questions
Solution
(1) From the regular structure of the function $I_{\rm Out}(I_{\rm In})$ one can see that it is a block interleaver ⇒ Response 1.
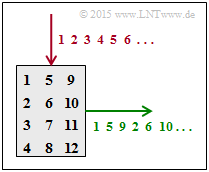
(2) The index "1" is output as the first character. Further applies:
- The index 5 is output as the second character ⇒ $\underline{N_{\rm R} = 4}$.
- The index 2 is output as the fourth character ⇒ $\underline{N_{\rm C} = 3}$.
The upper graph shows for the $4×3$ interleaver matrix:
- the column-by-column write $($red$)$,
- the row-by-row readout $($green$)$.
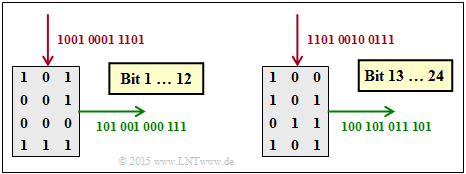
(3) Correct is the proposed solution 2:
- The matrix is written column-by-column and read row-by-row.
- After $12$ bits, the matrix is cleared and the procedure starts again.
- The graphic shows that the solution suggestion 2 is correct.
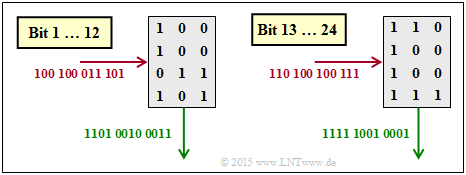
(4) Correct is the proposed solution 1:
- In de-interleaving, the matrix is written row-by-row and read column-by-column.
- The graphic shows that here the solution suggestion 1 is correct.