Difference between revisions of "Information Theory/Discrete Sources with Memory"
m (Guenter moved page Information Theory/Sources with Memory to Information Theory/Discrete Sources with Memory) |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 20: | Line 20: | ||
Due to the unequal symbol probabilities the entropy is smaller than the decision content $H_0 = \log_2 M = 2 \hspace{0.05cm}. \rm bit/symbol$. | Due to the unequal symbol probabilities the entropy is smaller than the decision content $H_0 = \log_2 M = 2 \hspace{0.05cm}. \rm bit/symbol$. | ||
| − | [[File:EN_Inf_T_1_2_S1a.png|right|frame|Quaternary | + | [[File:EN_Inf_T_1_2_S1a.png|right|frame|Quaternary source without/with memory]] |
<br><br> | <br><br> | ||
The source $\rm Q2$ is almost identical to the source $\rm Q1$, except that each individual symbol is output not only once, but twice in a row: $\rm A ⇒ AA$, $\rm B ⇒ BB$, and so on. | The source $\rm Q2$ is almost identical to the source $\rm Q1$, except that each individual symbol is output not only once, but twice in a row: $\rm A ⇒ AA$, $\rm B ⇒ BB$, and so on. | ||
*It is obvious that $\rm Q2$ has a smaller entropy (uncertainty) than $\rm Q1$. | *It is obvious that $\rm Q2$ has a smaller entropy (uncertainty) than $\rm Q1$. | ||
| − | *Because of the simple repetition code, | + | *Because of the simple repetition code, the entropy |
:$$H = 1.84/2 = 0.92 \hspace{0.05cm} \rm bit/symbol$$ | :$$H = 1.84/2 = 0.92 \hspace{0.05cm} \rm bit/symbol$$ | ||
| − | :only half the size, although the occurrence probabilities have not changed.}} | + | :has only half the size, although the occurrence probabilities have not changed.}} |
| Line 33: | Line 33: | ||
This example shows: | This example shows: | ||
*The entropy of a source with memory is smaller than the entropy of a memoryless source with equal symbol probabilities. | *The entropy of a source with memory is smaller than the entropy of a memoryless source with equal symbol probabilities. | ||
| − | *The statistical | + | *The statistical bindings within the sequence $〈 q_ν 〉$ have to be considered now, |
*namely the dependency of the symbol $q_ν$ from the predecessor symbols $q_{ν-1}$, $q_{ν-2}$, ... }} | *namely the dependency of the symbol $q_ν$ from the predecessor symbols $q_{ν-1}$, $q_{ν-2}$, ... }} | ||
| Line 40: | Line 40: | ||
<br> | <br> | ||
We continue to look at the source symbol sequence $〈 q_1, \hspace{0.05cm} q_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, q_{ν-1}, \hspace{0.05cm}q_ν, \hspace{0.05cm}\hspace{0.05cm}q_{ν+1} .\hspace{0.05cm}\text{...} \hspace{0.05cm}〉$ and now consider the entropy of two successive source symbols. | We continue to look at the source symbol sequence $〈 q_1, \hspace{0.05cm} q_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, q_{ν-1}, \hspace{0.05cm}q_ν, \hspace{0.05cm}\hspace{0.05cm}q_{ν+1} .\hspace{0.05cm}\text{...} \hspace{0.05cm}〉$ and now consider the entropy of two successive source symbols. | ||
| − | *All source symbols $q_ν$ are taken from an alphabet with the symbol | + | *All source symbols $q_ν$ are taken from an alphabet with the symbol set size $M$, so that for the combination $(q_ν, \hspace{0.05cm}q_{ν+1})$ there are exactly $M^2$ possible symbol pairs with the following [[Theory_of_Stochastic_Signals/Set Theory Basics#Intersection|combined probabilities]]: |
:$${\rm Pr}(q_{\nu}\cap q_{\nu+1})\le {\rm Pr}(q_{\nu}) \cdot {\rm Pr}( q_{\nu+1}) | :$${\rm Pr}(q_{\nu}\cap q_{\nu+1})\le {\rm Pr}(q_{\nu}) \cdot {\rm Pr}( q_{\nu+1}) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *From this, the ''compound entropy'' of | + | *From this, the '''compound entropy''' of two consecutive symbols can be computed: |
| − | :$$H_2\hspace{0.05cm}' = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} \sum_{q_{\nu+1}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm} q_{\mu}\hspace{0.01cm} \}}\hspace{-0.1cm}{\rm Pr}(q_{\nu}\cap q_{\nu+1}) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu}\cap q_{\nu+1})} \hspace{0.4cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/ | + | :$$H_2\hspace{0.05cm}' = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} \ \sum_{q_{\nu+1}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm} q_{\mu}\hspace{0.01cm} \}}\hspace{-0.1cm}{\rm Pr}(q_{\nu}\cap q_{\nu+1}) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu}\cap q_{\nu+1})} \hspace{0.4cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/two–tuple}) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | :The index "2" symbolizes that the entropy thus calculated refers to two-tuples. | + | :The index "2" symbolizes that the entropy thus calculated refers to '''two-tuples'''. |
| − | + | *To get the average information content per symbol, $H_2\hspace{0.05cm}'$ has to be divided in half: | |
| − | To get the average information content per symbol, $H_2\hspace{0.05cm}'$ has to be divided in half: | ||
:$$H_2 = {H_2\hspace{0.05cm}'}/{2} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) | :$$H_2 = {H_2\hspace{0.05cm}'}/{2} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | In order to achieve a consistent nomenclature, we now label the entropy defined in chapter [[Information_Theory/Discrete Memoryless Sources#Model_and_Prerequisites|Memoryless Message Sources]] with $H_1$: | + | *In order to achieve a consistent nomenclature, we now label the entropy defined in chapter [[Information_Theory/Discrete Memoryless Sources#Model_and_Prerequisites|Memoryless Message Sources]] with $H_1$: |
:$$H_1 = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} {\rm Pr}(q_{\nu}) \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu})} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) | :$$H_1 = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} {\rm Pr}(q_{\nu}) \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu})} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | The index "1" is supposed to indicate that $H_1$ considers only the symbol probabilities and not statistical | + | *The index "1" is supposed to indicate that $H_1$ considers only the symbol probabilities and not statistical bindings between symbols within the sequence. With the decision content $H_0 = \log_2 \ M$ the following size relation results: |
$$H_0 \ge H_1 \ge H_2 | $$H_0 \ge H_1 \ge H_2 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | With statistical independence of the sequence elements $H_2 = H_1$. | + | *With statistical independence of the sequence elements ⇒ $H_2 = H_1$. |
| − | The previous equations each indicate | + | |
| + | The previous equations each indicate an "ensemble mean value". The probabilities required for the calculation of $H_1$ and $H_2$ can, however, also be calculated as time averages from a very long sequence or, more precisely, approximated by the corresponding [[Theory_of_Stochastic_Signals/From Random Experiment to Random Variable#Bernoulli's_Law_of_Large_Numbers|relative frequencies]]. | ||
Let us now illustrate the calculation of entropy approximations $H_1$ and $H_2$ with three examples. | Let us now illustrate the calculation of entropy approximations $H_1$ and $H_2$ with three examples. | ||
| + | [[File:Inf_T_1_2_S2_vers2.png|right|frame|Ternary symbol sequence and formation of two-tuples]] | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 2:}$ | $\text{Example 2:}$ | ||
| − | We will first look at the sequence $〈 q_1$, ... , $q_{50} \rangle $ according to the graphic, where the sequence elements $q_ν$ originate from the alphabet $\rm \{A, \ B, \ C \}$ ⇒ the symbol | + | We will first look at the sequence $〈 q_1$, ... , $q_{50} \rangle $ according to the graphic, where the sequence elements $q_ν$ originate from the alphabet $\rm \{A, \ B, \ C \}$ ⇒ the symbol set size is $M = 3$. |
| − | |||
| − | |||
By time averaging over the $50$ symbols one gets the symbol probabilities $p_{\rm A} ≈ 0.5$, $p_{\rm B} ≈ 0.3$ and $p_{\rm C} ≈ 0.2$, with which one can calculate the first order entropy approximation: | By time averaging over the $50$ symbols one gets the symbol probabilities $p_{\rm A} ≈ 0.5$, $p_{\rm B} ≈ 0.3$ and $p_{\rm C} ≈ 0.2$, with which one can calculate the first order entropy approximation: | ||
| Line 100: | Line 99: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 3:}$ | $\text{Example 3:}$ | ||
| − | Now let us consider a ''memoryless binary source'' with equally probable symbols, i.e. there would be $p_{\rm A} = p_{\rm B} = 1/2$. The first twenty subsequent elements are $〈 q_ν 〉 =\rm BBAAABAABBBBBAAAABABAB$ ... | + | Now let us consider a '''memoryless binary source''' with equally probable symbols, i.e. there would be $p_{\rm A} = p_{\rm B} = 1/2$. The first twenty subsequent elements are $〈 q_ν 〉 =\rm BBAAABAABBBBBAAAABABAB$ ... |
*Because of the equally probable binary symbols $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$. | *Because of the equally probable binary symbols $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$. | ||
| − | *The compound probability $p_{\rm AB}$ of the combination $\rm AB$ is equal to $p_{\rm A} | + | *The compound probability $p_{\rm AB}$ of the combination $\rm AB$ is equal to $p_{\rm A} \cdot p_{\rm B} = 1/4$. Also $p_{\rm AA} = p_{\rm BB} = p_{\rm BA} = 1/4$. |
*This gives for the second entropy approximation | *This gives for the second entropy approximation | ||
| Line 115: | Line 114: | ||
The third sequence considered here results from the binary sequence of $\text{Example 3}$ by using a simple repeat code: | The third sequence considered here results from the binary sequence of $\text{Example 3}$ by using a simple repeat code: | ||
:$$〈 q_ν 〉 =\rm BbBbAaAaAaBbAaAaBbBb \text{...} $$ | :$$〈 q_ν 〉 =\rm BbBbAaAaAaBbAaAaBbBb \text{...} $$ | ||
| − | *The repeated symbols are marked by corresponding lower case letters. | + | *The repeated symbols are marked by corresponding lower case letters. But it still applies $M=2$. |
*Because of the equally probable binary symbols, this also results in $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$. | *Because of the equally probable binary symbols, this also results in $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$. | ||
*As shown in [[Aufgaben:1.3_Entropienäherungen|Exercise 1.3]] for the compound probabilities we obtain $p_{\rm AA}=p_{\rm BB} = 3/8$ and $p_{\rm AB}=p_{\rm BA} = 1/8$. Hence | *As shown in [[Aufgaben:1.3_Entropienäherungen|Exercise 1.3]] for the compound probabilities we obtain $p_{\rm AA}=p_{\rm BB} = 3/8$ and $p_{\rm AB}=p_{\rm BA} = 1/8$. Hence | ||
| Line 123: | Line 122: | ||
A closer look at the task at hand leads to the following conclusion: | A closer look at the task at hand leads to the following conclusion: | ||
| − | *The entropy should actually be $H = 0.5 \hspace{0.05cm} \rm bit/symbol$ | + | *The entropy should actually be $H = 0.5 \hspace{0.05cm} \rm bit/symbol$ (every second symbol does not provide new information) |
| − | *The second entropy approximation $H_2 = 0.906 \hspace{0.05cm} \rm bit/symbol$ | + | *The second entropy approximation $H_2 = 0.906 \hspace{0.05cm} \rm bit/symbol$ is much larger than the entropy $H$. |
| − | *For the determination | + | *For the entropy determination, the second order approximation is not sufficient. Rather, one must consider larger contiguous blocks of $k > 2$ symbols. |
| − | *In the following, such a block is referred to as $k$ | + | *In the following, such a block is referred to as "$k$–tuple".}} |
==Generalization to $k$-tuple and boundary crossing == | ==Generalization to $k$-tuple and boundary crossing == | ||
<br> | <br> | ||
| − | For abbreviation we write using the compound probability $p_i^{(k)}$ a $k$ | + | For abbreviation we write using the compound probability $p_i^{(k)}$ for a $k$–tuple in general: |
| − | :$$H_k = \frac{1}{k} \cdot \sum_{i=1}^{M^k} p_i^{(k)} \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{p_i^{(k)}} \hspace{0.5cm}({\rm | + | :$$H_k = \frac{1}{k} \cdot \sum_{i=1}^{M^k} p_i^{(k)} \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{p_i^{(k)}} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | The control variable $i$ stands for one of the $M^k$ | + | *The control variable $i$ stands for one of the $M^k$ tuples. |
| + | *The previously calculated approximation $H_2$ results with $k = 2$. | ||
| + | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | The ''' | + | The '''entropy of a discrete source with memory''' has the following limit: |
:$$H = \lim_{k \rightarrow \infty }H_k \hspace{0.05cm}.$$ | :$$H = \lim_{k \rightarrow \infty }H_k \hspace{0.05cm}.$$ | ||
| − | For the ''entropy approximations'' $H_k$ the following relations apply $(H_0$ is the decision content$)$: | + | For the '''entropy approximations''' $H_k$ the following relations apply $(H_0$ is the decision content$)$: |
:$$H \le \text{...} \le H_k \le \text{...} \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$}} | :$$H \le \text{...} \le H_k \le \text{...} \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$}} | ||
| − | The computational effort will increase with increasing $k$ except for a few special cases (see the following example) and depends on the symbol size $M$ of course: | + | The computational effort will increase with increasing $k$ except for a few special cases (see the following example) and depends on the symbol set size $M$ of course: |
| − | *For the calculation of $H_{10}$ a binary source $(M = 2)$ | + | *For the calculation of $H_{10}$ for a binary source $(M = 2)$ one must average over $2^{10} = 1024$ terms. |
*With each further increase of $k$ by $1$ the number of sum terms doubles. | *With each further increase of $k$ by $1$ the number of sum terms doubles. | ||
| − | *In case of a quaternary source $(M = 4)$ it must already be averaged over $4^{10} = 1\hspace{0.08cm}048\hspace{0.08cm}576$ summation terms | + | *In case of a quaternary source $(M = 4)$ it must already be averaged over $4^{10} = 1\hspace{0.08cm}048\hspace{0.08cm}576$ summation terms for the determination of $H_{10}$. |
| − | * Considering that each of these $4^{10} =2^{20} >10^6$ $k$ | + | * Considering that each of these $4^{10} =2^{20} >10^6$ $k$–tuple should occur in simulation/time averaging about $100$ times (statistical guideline) to ensure sufficient simulation accuracy, it follows that the sequence length should be in this case greater than $N = 10^8$. |
| Line 164: | Line 165: | ||
| − | The | + | The entropy of this alternating binary sequence is therefore |
:$$H = \lim_{k \rightarrow \infty }{1}/{k} = 0 \hspace{0.05cm}.$$ | :$$H = \lim_{k \rightarrow \infty }{1}/{k} = 0 \hspace{0.05cm}.$$ | ||
| − | The result was to be expected, since the considered sequence has only minimal information, which does not affect the entropy end value $H$ namely: <br> "Does $\rm A$ occur at the even or the odd times?" | + | The result was to be expected, since the considered sequence has only minimal information, which does not affect the entropy end value $H$, namely: <br> "Does $\rm A$ occur at the even or the odd times?" |
You can see that $H_k$ comes closer to this final value $H = 0$ very slowly: The twentieth entropy approximation still returns $H_{20} = 0.05 \hspace{0.05cm} \rm bit/symbol$. }} | You can see that $H_k$ comes closer to this final value $H = 0$ very slowly: The twentieth entropy approximation still returns $H_{20} = 0.05 \hspace{0.05cm} \rm bit/symbol$. }} | ||
| Line 176: | Line 177: | ||
$\text{Summary of the results of the last pages:}$ | $\text{Summary of the results of the last pages:}$ | ||
| − | *Generally it applies to the ''' | + | *Generally it applies to the '''entropy of a message source''': |
:$$H \le \text{...} \le H_3 \le H_2 \le H_1 \le H_0 | :$$H \le \text{...} \le H_3 \le H_2 \le H_1 \le H_0 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *A '''redundancy-free source'' exists if all $M$ symbols are equally probable and there are no statistical | + | *A '''redundancy-free source''' exists if all $M$ symbols are equally probable and there are no statistical bindings within the sequence. <br> For these hold $(r$ denotes the ''relative redundancy'' $)$: |
:$$H = H_0 = H_1 = H_2 = H_3 = \text{...}\hspace{0.5cm} | :$$H = H_0 = H_1 = H_2 = H_3 = \text{...}\hspace{0.5cm} | ||
\Rightarrow \hspace{0.5cm} r = \frac{H - H_0}{H_0}= 0 \hspace{0.05cm}.$$ | \Rightarrow \hspace{0.5cm} r = \frac{H - H_0}{H_0}= 0 \hspace{0.05cm}.$$ | ||
| − | *A '''memoryless source''' can be quite redundant $(r> 0)$. This redundancy then is solely due to the deviation of the symbol probabilities from the uniform distribution. Here the following relations are valid | + | *A '''memoryless source''' can be quite redundant $(r> 0)$. This redundancy then is solely due to the deviation of the symbol probabilities from the uniform distribution. Here the following relations are valid: |
:$$H = H_1 = H_2 = H_3 = \text{...} \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}0 \le r = \frac{H_1 - H_0}{H_0}< 1 \hspace{0.05cm}.$$ | :$$H = H_1 = H_2 = H_3 = \text{...} \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}0 \le r = \frac{H_1 - H_0}{H_0}< 1 \hspace{0.05cm}.$$ | ||
*The corresponding condition for a '''source with memory''' is | *The corresponding condition for a '''source with memory''' is | ||
:$$ H <\text{...} < H_3 < H_2 < H_1 \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} 0 < r = \frac{H_1 - H_0}{H_0}\le1 \hspace{0.05cm}.$$ | :$$ H <\text{...} < H_3 < H_2 < H_1 \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} 0 < r = \frac{H_1 - H_0}{H_0}\le1 \hspace{0.05cm}.$$ | ||
*If $H_2 < H_1$, then $H_3 < H_2$, $H_4 < H_3$, etc. ⇒ In the general equation, the "≤" character must be replaced by the "<" character. | *If $H_2 < H_1$, then $H_3 < H_2$, $H_4 < H_3$, etc. ⇒ In the general equation, the "≤" character must be replaced by the "<" character. | ||
| − | *If the symbols are equally probable, then again $H_1 = H_0$, while $H_1 < H_0$ applies to symbols which are not equally probable.}} | + | *If the symbols are equally probable, then again $H_1 = H_0$, while $H_1 < H_0$ applies to symbols which are not equally probable.}} |
| − | ==The | + | ==The entropy of the AMI code == |
<br> | <br> | ||
| − | In chapter [[Digital_Signal_Transmission/Symbol-Wise Coding with Pseudo Ternary Codes#Properties_of_AMI Code|Symbol-wise Coding with Pseudo-Ternary Codes]] of the book "Digital Signal Transmission", among other things, the AMI pseudo-ternary code is discussed. | + | In chapter [[Digital_Signal_Transmission/Symbol-Wise Coding with Pseudo Ternary Codes#Properties_of_AMI Code|Symbol-wise Coding with Pseudo-Ternary Codes]] of the book "Digital Signal Transmission", among other things, the AMI pseudo-ternary code is discussed. |
| + | [[File:EN_Inf_T_1_2_S4.png|right|frame|Signals and symbol sequences for AMI code]] | ||
| + | |||
*This converts the binary sequence $〈 q_ν 〉$ with $q_ν ∈ \{ \rm L, \ H \}$ into the ternary sequence $〈 c_ν 〉$ with $q_ν ∈ \{ \rm M, \ N, \ P \}$. | *This converts the binary sequence $〈 q_ν 〉$ with $q_ν ∈ \{ \rm L, \ H \}$ into the ternary sequence $〈 c_ν 〉$ with $q_ν ∈ \{ \rm M, \ N, \ P \}$. | ||
| − | *The names of the source symbols stand for $\rm L$ow and $\rm H$igh and those of the code symbols for $\rm M$inus, $\rm | + | *The names of the source symbols stand for $\rm L$(ow) and $\rm H$(igh) and those of the code symbols for $\rm M$(inus), $\rm P$(lus), and $\rm N$(ull) ⇒ "Zero". |
| − | The coding rule of the AMI code ("Alternate Mark Inversion") is | + | The coding rule of the AMI code ("Alternate Mark Inversion") is: |
| − | |||
*Each binary symbol $q_ν =\rm L$ is represented by the code symbol $c_ν =\rm N$ . | *Each binary symbol $q_ν =\rm L$ is represented by the code symbol $c_ν =\rm N$ . | ||
| − | *In contrast, $q_ν =\rm H$ alternates with $c_ν =\rm P$ and $c_ν =\rm M$ coded ⇒ name " | + | *In contrast, $q_ν =\rm H$ alternates with $c_ν =\rm P$ and $c_ν =\rm M$ coded ⇒ name "Alternate Mark Inversion". |
| − | + | *This special encoding adds redundancy with the sole purpose of ensuring that the code sequence does not contain a DC component. | |
| − | |||
| − | This special encoding adds redundancy with the sole purpose of ensuring that the code sequence does not contain a DC component. | ||
<br clear=all> | <br clear=all> | ||
However, we do not consider the spectral properties of the AMI code here, but interpret this code information-theoretically: | However, we do not consider the spectral properties of the AMI code here, but interpret this code information-theoretically: | ||
| − | *Based on the | + | *Based on the symbol set size $M = 3$ the decision content of the (ternary) code sequence is equal to $H_0 = \log_2 \ 3 ≈ 1.585 \hspace{0.05cm} \rm bit/symbol$. The first entropy approximation returns $H_1 = 1.5 \hspace{0.05cm} \rm bit/Symbol$, as shown in the following calculation: |
:$$p_{\rm H} = p_{\rm L} = 1/2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$$p_{\rm H} = p_{\rm L} = 1/2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Line 214: | Line 214: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Let's now look at two-tuples. With AMI code, $\rm P$ cannot follow $\rm P$ and $\rm M$ cannot follow $\rm M$ | + | *Let's now look at two-tuples. With the AMI code, $\rm P$ cannot follow $\rm P$ and $\rm M$ cannot follow $\rm M$. The probability for $\rm NN$ is equal to $p_{\rm L} \cdot p_{\rm L} = 1/4$. All other (six) two-tuples occur with the probability $1/8$. From this follows for the second entropy approximation: |
:$$H_2 = 1/2 \cdot \big [ 1/4 \cdot {\rm log_2}\hspace{0.1cm}4 + 6 \cdot 1/8 \cdot {\rm log_2}\hspace{0.1cm}8 \big ] = 1,375 \,{\rm bit/symbol} \hspace{0.05cm}.$$ | :$$H_2 = 1/2 \cdot \big [ 1/4 \cdot {\rm log_2}\hspace{0.1cm}4 + 6 \cdot 1/8 \cdot {\rm log_2}\hspace{0.1cm}8 \big ] = 1,375 \,{\rm bit/symbol} \hspace{0.05cm}.$$ | ||
| Line 220: | Line 220: | ||
:$$ H < \hspace{0.05cm}\text{...}\hspace{0.05cm} < H_5 < H_4 < H_3 < H_2 = 1.375 \,{\rm bit/symbol} \hspace{0.05cm}.$$ | :$$ H < \hspace{0.05cm}\text{...}\hspace{0.05cm} < H_5 < H_4 < H_3 < H_2 = 1.375 \,{\rm bit/symbol} \hspace{0.05cm}.$$ | ||
| − | *Exceptionally in this example we know the actual entropy $H$ of the code symbol sequence $〈 c_ν 〉$: | + | *Exceptionally in this example we know the actual entropy $H$ of the code symbol sequence $〈 c_ν 〉$: Since no new information is added by the coder and no information is lost, it is the same entropy $H = 1 \,{\rm bit/symbol} $ as the one of the redundancy-free binary sequence $〈 q_ν 〉$. |
| − | The [[Aufgaben:1.4_Entropienäherungen_für_den_AMI-Code|Exercise 1.4]] shows the considerable effort required to calculate the entropy approximation $H_3$. Moreover, $H_3$ still deviates significantly from the final value $H = 1 \,{\rm bit/symbol} $. A faster result is achieved if the AMI code is described by a | + | The [[Aufgaben:1.4_Entropienäherungen_für_den_AMI-Code|Exercise 1.4]] shows the considerable effort required to calculate the entropy approximation $H_3$. Moreover, $H_3$ still deviates significantly from the final value $H = 1 \,{\rm bit/symbol} $. A faster result is achieved if the AMI code is described by a Markov chain as explained in the next section. |
Revision as of 14:28, 17 June 2021
Contents
A simple introductory example
$\text{Example 1:}$ At the beginning of the first chapter we have considered a memoryless message source with the symbol set $\rm \{A, \ B, \ C, \ D\}$ ⇒ $M = 4$ . An exemplary symbol sequence is shown again in the following figure as source $\rm Q1$ .
With the symbol probabilities $p_{\rm A} = 0.4 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.3 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.2 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.1\hspace{0.05cm}$ the entropy is
- $$H \hspace{-0.05cm}= 0.4 \cdot {\rm log}_2\hspace{0.05cm}\frac {1}{0.4} + 0.3 \cdot {\rm log}_2\hspace{0.05cm}\frac {1}{0.3} + 0.2 \cdot {\rm log}_2\hspace{0.05cm}\frac {1}{0.2} + 0.1 \cdot {\rm log}_2\hspace{0.05cm}\frac {1}{0.1} \approx 1.84 \hspace{0.05cm}{\rm bit/symbol} \hspace{0.01cm}.$$
Due to the unequal symbol probabilities the entropy is smaller than the decision content $H_0 = \log_2 M = 2 \hspace{0.05cm}. \rm bit/symbol$.
The source $\rm Q2$ is almost identical to the source $\rm Q1$, except that each individual symbol is output not only once, but twice in a row: $\rm A ⇒ AA$, $\rm B ⇒ BB$, and so on.
- It is obvious that $\rm Q2$ has a smaller entropy (uncertainty) than $\rm Q1$.
- Because of the simple repetition code, the entropy
- $$H = 1.84/2 = 0.92 \hspace{0.05cm} \rm bit/symbol$$
- has only half the size, although the occurrence probabilities have not changed.
$\text{Conclusion:}$ This example shows:
- The entropy of a source with memory is smaller than the entropy of a memoryless source with equal symbol probabilities.
- The statistical bindings within the sequence $〈 q_ν 〉$ have to be considered now,
- namely the dependency of the symbol $q_ν$ from the predecessor symbols $q_{ν-1}$, $q_{ν-2}$, ...
Entropy with respect to two-tuples
We continue to look at the source symbol sequence $〈 q_1, \hspace{0.05cm} q_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, q_{ν-1}, \hspace{0.05cm}q_ν, \hspace{0.05cm}\hspace{0.05cm}q_{ν+1} .\hspace{0.05cm}\text{...} \hspace{0.05cm}〉$ and now consider the entropy of two successive source symbols.
- All source symbols $q_ν$ are taken from an alphabet with the symbol set size $M$, so that for the combination $(q_ν, \hspace{0.05cm}q_{ν+1})$ there are exactly $M^2$ possible symbol pairs with the following combined probabilities:
- $${\rm Pr}(q_{\nu}\cap q_{\nu+1})\le {\rm Pr}(q_{\nu}) \cdot {\rm Pr}( q_{\nu+1}) \hspace{0.05cm}.$$
- From this, the compound entropy of two consecutive symbols can be computed:
- $$H_2\hspace{0.05cm}' = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} \ \sum_{q_{\nu+1}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm} q_{\mu}\hspace{0.01cm} \}}\hspace{-0.1cm}{\rm Pr}(q_{\nu}\cap q_{\nu+1}) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu}\cap q_{\nu+1})} \hspace{0.4cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/two–tuple}) \hspace{0.05cm}.$$
- The index "2" symbolizes that the entropy thus calculated refers to two-tuples.
- To get the average information content per symbol, $H_2\hspace{0.05cm}'$ has to be divided in half:
- $$H_2 = {H_2\hspace{0.05cm}'}/{2} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) \hspace{0.05cm}.$$
- In order to achieve a consistent nomenclature, we now label the entropy defined in chapter Memoryless Message Sources with $H_1$:
- $$H_1 = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} {\rm Pr}(q_{\nu}) \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu})} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) \hspace{0.05cm}.$$
- The index "1" is supposed to indicate that $H_1$ considers only the symbol probabilities and not statistical bindings between symbols within the sequence. With the decision content $H_0 = \log_2 \ M$ the following size relation results:
$$H_0 \ge H_1 \ge H_2 \hspace{0.05cm}.$$
- With statistical independence of the sequence elements ⇒ $H_2 = H_1$.
The previous equations each indicate an "ensemble mean value". The probabilities required for the calculation of $H_1$ and $H_2$ can, however, also be calculated as time averages from a very long sequence or, more precisely, approximated by the corresponding relative frequencies.
Let us now illustrate the calculation of entropy approximations $H_1$ and $H_2$ with three examples.
$\text{Example 2:}$ We will first look at the sequence $〈 q_1$, ... , $q_{50} \rangle $ according to the graphic, where the sequence elements $q_ν$ originate from the alphabet $\rm \{A, \ B, \ C \}$ ⇒ the symbol set size is $M = 3$.
By time averaging over the $50$ symbols one gets the symbol probabilities $p_{\rm A} ≈ 0.5$, $p_{\rm B} ≈ 0.3$ and $p_{\rm C} ≈ 0.2$, with which one can calculate the first order entropy approximation:
- $$H_1 = 0.5 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.5} + 0.3 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.3} + 0.2 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.2} \approx \, 1.486 \,{\rm bit/symbol} \hspace{0.05cm}.$$
Due to the not equally probable symbols $H_1 < H_0 = 1.585 \hspace{0.05cm}. \rm bit/symbol$. As an approximation for the probabilities of two-tuples one gets from the above sequence:
- $$\begin{align*}p_{\rm AA} \hspace{-0.1cm}& = \hspace{-0.1cm} 14/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm AB} = 8/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm AC} = 3/49\hspace{0.05cm}, \\\ p_{\rm BA} \hspace{-0.1cm}& = \hspace{0.07cm} 7/49\hspace{0.05cm}, \hspace{0.25cm}p_{\rm BB} = 2/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm BC} = 5/49\hspace{0.05cm}, \\\ p_{\rm CA} \hspace{-0.1cm}& = \hspace{0.07cm} 4/49\hspace{0.05cm}, \hspace{0.25cm}p_{\rm CB} = 5/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm CC} = 1/49\hspace{0.05cm}.\end{align*}$$
Please note that the $50$ sequence elements can only be formed from $49$ two-tuples $(\rm AA$, ... , $\rm CC)$ which are marked in different colors in the graphic.
- The entropy approximation $H_2$ should actually be equal to $H_1$ since the given symbol sequence comes from a memoryless source.
- Because of the short sequence length $N = 50$ and the resulting statistical inaccuracy, however, a smaller value results:
- $$H_2 ≈ 1.39\hspace{0.05cm} \rm bit/symbol.$$
$\text{Example 3:}$ Now let us consider a memoryless binary source with equally probable symbols, i.e. there would be $p_{\rm A} = p_{\rm B} = 1/2$. The first twenty subsequent elements are $〈 q_ν 〉 =\rm BBAAABAABBBBBAAAABABAB$ ...
- Because of the equally probable binary symbols $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$.
- The compound probability $p_{\rm AB}$ of the combination $\rm AB$ is equal to $p_{\rm A} \cdot p_{\rm B} = 1/4$. Also $p_{\rm AA} = p_{\rm BB} = p_{\rm BA} = 1/4$.
- This gives for the second entropy approximation
- $$H_2 = {1}/{2} \cdot \big [ {1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 + {1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 +{1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 +{1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 \big ] = 1 \,{\rm bit/symbol} = H_1 = H_0 \hspace{0.05cm}.$$
Note: Due to the short length of the given sequence the probabilities are slightly different: $p_{\rm AA} = 6/19$, $p_{\rm BB} = 5/19$, $p_{\rm AB} = p_{\rm BA} = 4/19$.
$\text{Example 4:}$ The third sequence considered here results from the binary sequence of $\text{Example 3}$ by using a simple repeat code:
- $$〈 q_ν 〉 =\rm BbBbAaAaAaBbAaAaBbBb \text{...} $$
- The repeated symbols are marked by corresponding lower case letters. But it still applies $M=2$.
- Because of the equally probable binary symbols, this also results in $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$.
- As shown in Exercise 1.3 for the compound probabilities we obtain $p_{\rm AA}=p_{\rm BB} = 3/8$ and $p_{\rm AB}=p_{\rm BA} = 1/8$. Hence
- $$\begin{align*}H_2 ={1}/{2} \cdot \big [ 2 \cdot {3}/{8} \cdot {\rm log}_2\hspace{0.1cm} {8}/{3} + 2 \cdot {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}8\big ] = {3}/{8} \cdot {\rm log}_2\hspace{0.1cm}8 - {3}/{8} \cdot{\rm log}_2\hspace{0.1cm}3 + {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}8 \approx 0.906 \,{\rm bit/symbol} < H_1 = H_0 \hspace{0.05cm}.\end{align*}$$
A closer look at the task at hand leads to the following conclusion:
- The entropy should actually be $H = 0.5 \hspace{0.05cm} \rm bit/symbol$ (every second symbol does not provide new information)
- The second entropy approximation $H_2 = 0.906 \hspace{0.05cm} \rm bit/symbol$ is much larger than the entropy $H$.
- For the entropy determination, the second order approximation is not sufficient. Rather, one must consider larger contiguous blocks of $k > 2$ symbols.
- In the following, such a block is referred to as "$k$–tuple".
Generalization to $k$-tuple and boundary crossing
For abbreviation we write using the compound probability $p_i^{(k)}$ for a $k$–tuple in general:
- $$H_k = \frac{1}{k} \cdot \sum_{i=1}^{M^k} p_i^{(k)} \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{p_i^{(k)}} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) \hspace{0.05cm}.$$
- The control variable $i$ stands for one of the $M^k$ tuples.
- The previously calculated approximation $H_2$ results with $k = 2$.
$\text{Definition:}$ The entropy of a discrete source with memory has the following limit:
- $$H = \lim_{k \rightarrow \infty }H_k \hspace{0.05cm}.$$
For the entropy approximations $H_k$ the following relations apply $(H_0$ is the decision content$)$:
- $$H \le \text{...} \le H_k \le \text{...} \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$
The computational effort will increase with increasing $k$ except for a few special cases (see the following example) and depends on the symbol set size $M$ of course:
- For the calculation of $H_{10}$ for a binary source $(M = 2)$ one must average over $2^{10} = 1024$ terms.
- With each further increase of $k$ by $1$ the number of sum terms doubles.
- In case of a quaternary source $(M = 4)$ it must already be averaged over $4^{10} = 1\hspace{0.08cm}048\hspace{0.08cm}576$ summation terms for the determination of $H_{10}$.
- Considering that each of these $4^{10} =2^{20} >10^6$ $k$–tuple should occur in simulation/time averaging about $100$ times (statistical guideline) to ensure sufficient simulation accuracy, it follows that the sequence length should be in this case greater than $N = 10^8$.
$\text{Example 5:}$ We consider an alternating binary sequence ⇒ $〈 q_ν 〉 =\rm ABABABAB$ ... . Accordingly it holds that $H_0 = H_1 = 1 \hspace{0.1cm} \rm bit/symbol$.
In this special case, the $H_k$ approximation must be determined independently from $k$ by averaging only two compound probabilities:
- $k = 2$: $p_{\rm AB} = p_{\rm BA} = 1/2$ ⇒ $H_2 = 1/2 \hspace{0.2cm} \rm bit/symbol$,
- $k = 3$: $p_{\rm ABA} = p_{\rm BAB} = 1/2$ ⇒ $H_3 = 1/3 \hspace{0.2cm} \rm bit/symbol$,
- $k = 4$: $p_{\rm ABAB} = p_{\rm BABA} = 1/2$ ⇒ $H_4 = 1/4 \hspace{0.2cm} \rm bit/symbol$.
The entropy of this alternating binary sequence is therefore
- $$H = \lim_{k \rightarrow \infty }{1}/{k} = 0 \hspace{0.05cm}.$$
The result was to be expected, since the considered sequence has only minimal information, which does not affect the entropy end value $H$, namely:
"Does $\rm A$ occur at the even or the odd times?"
You can see that $H_k$ comes closer to this final value $H = 0$ very slowly: The twentieth entropy approximation still returns $H_{20} = 0.05 \hspace{0.05cm} \rm bit/symbol$.
$\text{Summary of the results of the last pages:}$
- Generally it applies to the entropy of a message source:
- $$H \le \text{...} \le H_3 \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$
- A redundancy-free source exists if all $M$ symbols are equally probable and there are no statistical bindings within the sequence.
For these hold $(r$ denotes the relative redundancy $)$:
- $$H = H_0 = H_1 = H_2 = H_3 = \text{...}\hspace{0.5cm} \Rightarrow \hspace{0.5cm} r = \frac{H - H_0}{H_0}= 0 \hspace{0.05cm}.$$
- A memoryless source can be quite redundant $(r> 0)$. This redundancy then is solely due to the deviation of the symbol probabilities from the uniform distribution. Here the following relations are valid:
- $$H = H_1 = H_2 = H_3 = \text{...} \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}0 \le r = \frac{H_1 - H_0}{H_0}< 1 \hspace{0.05cm}.$$
- The corresponding condition for a source with memory is
- $$ H <\text{...} < H_3 < H_2 < H_1 \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} 0 < r = \frac{H_1 - H_0}{H_0}\le1 \hspace{0.05cm}.$$
- If $H_2 < H_1$, then $H_3 < H_2$, $H_4 < H_3$, etc. ⇒ In the general equation, the "≤" character must be replaced by the "<" character.
- If the symbols are equally probable, then again $H_1 = H_0$, while $H_1 < H_0$ applies to symbols which are not equally probable.
The entropy of the AMI code
In chapter Symbol-wise Coding with Pseudo-Ternary Codes of the book "Digital Signal Transmission", among other things, the AMI pseudo-ternary code is discussed.
- This converts the binary sequence $〈 q_ν 〉$ with $q_ν ∈ \{ \rm L, \ H \}$ into the ternary sequence $〈 c_ν 〉$ with $q_ν ∈ \{ \rm M, \ N, \ P \}$.
- The names of the source symbols stand for $\rm L$(ow) and $\rm H$(igh) and those of the code symbols for $\rm M$(inus), $\rm P$(lus), and $\rm N$(ull) ⇒ "Zero".
The coding rule of the AMI code ("Alternate Mark Inversion") is:
- Each binary symbol $q_ν =\rm L$ is represented by the code symbol $c_ν =\rm N$ .
- In contrast, $q_ν =\rm H$ alternates with $c_ν =\rm P$ and $c_ν =\rm M$ coded ⇒ name "Alternate Mark Inversion".
- This special encoding adds redundancy with the sole purpose of ensuring that the code sequence does not contain a DC component.
However, we do not consider the spectral properties of the AMI code here, but interpret this code information-theoretically:
- Based on the symbol set size $M = 3$ the decision content of the (ternary) code sequence is equal to $H_0 = \log_2 \ 3 ≈ 1.585 \hspace{0.05cm} \rm bit/symbol$. The first entropy approximation returns $H_1 = 1.5 \hspace{0.05cm} \rm bit/Symbol$, as shown in the following calculation:
- $$p_{\rm H} = p_{\rm L} = 1/2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm N} = p_{\rm L} = 1/2\hspace{0.05cm},\hspace{0.2cm}p_{\rm M} = p_{\rm P}= p_{\rm H}/2 = 1/4\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_1 = 1/2 \cdot {\rm log}_2\hspace{0.1cm}2 + 2 \cdot 1/4 \cdot{\rm log}_2\hspace{0.1cm}4 = 1.5 \,{\rm bit/symbol} \hspace{0.05cm}.$$
- Let's now look at two-tuples. With the AMI code, $\rm P$ cannot follow $\rm P$ and $\rm M$ cannot follow $\rm M$. The probability for $\rm NN$ is equal to $p_{\rm L} \cdot p_{\rm L} = 1/4$. All other (six) two-tuples occur with the probability $1/8$. From this follows for the second entropy approximation:
- $$H_2 = 1/2 \cdot \big [ 1/4 \cdot {\rm log_2}\hspace{0.1cm}4 + 6 \cdot 1/8 \cdot {\rm log_2}\hspace{0.1cm}8 \big ] = 1,375 \,{\rm bit/symbol} \hspace{0.05cm}.$$
- For the further entropy approximations $H_3$, $H_4$, ... and the actual entropy $H$ will apply:
- $$ H < \hspace{0.05cm}\text{...}\hspace{0.05cm} < H_5 < H_4 < H_3 < H_2 = 1.375 \,{\rm bit/symbol} \hspace{0.05cm}.$$
- Exceptionally in this example we know the actual entropy $H$ of the code symbol sequence $〈 c_ν 〉$: Since no new information is added by the coder and no information is lost, it is the same entropy $H = 1 \,{\rm bit/symbol} $ as the one of the redundancy-free binary sequence $〈 q_ν 〉$.
The Exercise 1.4 shows the considerable effort required to calculate the entropy approximation $H_3$. Moreover, $H_3$ still deviates significantly from the final value $H = 1 \,{\rm bit/symbol} $. A faster result is achieved if the AMI code is described by a Markov chain as explained in the next section.
Binary sources with Markov properties
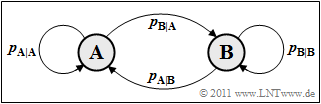
Sequences with statistical bonds between the sequence elements (symbols) are often modeled by Markov processes where we limit ourselves here to first-order Markov processes. First we consider a binary Markov process $(M = 2)$ with the states (symbols) $\rm A$ and $\rm B$.
On the right, you can see the transition diagram for a first-order binary Markov process however, only two of the four transfer probabilities given are freely selectable, for example
- $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = \rm Pr(A\hspace{0.01cm}|\hspace{0.01cm}B)$ ⇒ conditional probability that $\rm A$ follows $\rm B$ .
- $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}} = \rm Pr(B\hspace{0.01cm}|\hspace{0.01cm}A)$ ⇒ conditional probability that $\rm B$ follows $\rm A$ .
For the other two transition probabilities $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = 1- p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}$ and $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} = 1- p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}
\hspace{0.05cm}.$
Due to the presupposed properties Stationarity and Ergodicity the following applies to the state or symbol probabilities:
- $$p_{\rm A} = {\rm Pr}({\rm A}) = \frac{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}}{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}, \hspace{0.5cm}p_{\rm B} = {\rm Pr}({\rm B}) = \frac{p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}}{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}.$$
These equations allow first information theoretical statements about the Markov processes:
- For $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$ the symbols are equally likely ⇒ $p_{\text{A}} = p_{\text{B}}= 0.5$. The first entropy approximation returns $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$, independent of the actual values of the (conditional) transition probabilities $p_{\text{A|B}}$ or $p_{\text{B|A}}$.
- The source entropy $H$ as the threshold value $($for $k \to \infty)$ of the Entropy approximation $k$th order ⇒ $H_k$ but depends very much on the actual values of $p_{\text{A|B}}$ and $p_{\text{B|A}}$ and not only on their quotients. This is shown by the following example.
$\text{Example 6:}$ We consider three binary symmetric Markov sources that are represented by the numerical values of the symmetric transition probabilities $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} }$ . For the symbol probabilities the following applies: $p_{\rm A} = p_{\rm B}= 0.5$, and the other transition probabilities have the values
- $$p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 1 - p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}B} }.$$
- The middle (blue) symbol sequence with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.5$ has the entropy $H ≈ 1 \hspace{0.1cm} \rm bit/symbol$. That means: In this special case there are no statistical bonds within the sequence.
- The left (red) sequence with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.2$ has less changes between $\rm A$ and $\rm B$ and $\rm B$ Due to statistical dependencies between neighboring symbols the entropy is now smaller $H ≈ 0.72 \hspace{0.1cm} \rm bit/symbol$.
- The right (green) symbol sequence with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.8$ has the exact same entropy $H ≈ 0.72 \hspace{0.1cm} \rm bit/symbol$ as the red sequence. Here you can see many areas with alternating symbols $($... $\rm ABABAB$ ... $)$.
This example is worth noting:
- If you had not used the markup properties of the red and green sequences, you would have reached the respective result $H ≈ 0.72 \hspace{0.1cm} \rm bit/symbol$ only after lengthy calculations.
- The following pages show that for a source with mark properties the final value $H$ can be determined from the entropy approximations $H_1$ and $H_2$ alone. Likewise, all entropy approximations $H_1$ and $H_2$ can also be calculated from $H_k$ for $k$-tuples in a simple manner ⇒ $H_3$, $H_4$, $H_5$, ... $H_{100}$, ...
Simplified entropy calculation for Markov sources
We continue to assume the first-order symmetric binary Markov source. As on the previous page, we use the following nomenclature for
- the transition probabilities $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}}$, $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$, $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}A}}= 1- p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$, $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}B}} = 1 - p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}}$,
- the ergodic probabilities $p_{\text{A}}$ and $p_{\text{B}}$,
- the compound probabilities, for example $p_{\text{AB}} = p_{\text{A}} - p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$.
We now compute the Entropy of a two-tuple (with the unit "bit/two-tuple"):
- $$H_2\hspace{0.05cm}' = p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$
If one now replaces the logarithms of the products by corresponding sums of logarithms, one gets the result $H_2\hspace{0.05cm}' = H_1 + H_{\text{M}}$ with
- $$H_1 = p_{\rm A} \cdot (p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A})\cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm A}} + p_{\rm B} \cdot (p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B})\cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm B}} = p_{\rm A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm A}} + p_{\rm B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm B}} = H_{\rm bin} (p_{\rm A})= H_{\rm bin} (p_{\rm B}) \hspace{0.05cm},$$
- $$H_{\rm M}= p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$
$\text{Conclusion:}$ Thus the second entropy approximation (with the unit "bit/symbol"):
- $$H_2 = {1}/{2} \cdot {H_2\hspace{0.05cm}'} = {1}/{2} \cdot \big [ H_{\rm 1} + H_{\rm M} \big] \hspace{0.05cm}.$$
is to be noted:
- The first summand $H_1$ ⇒ first entropy approximation depends only on the symbol probabilities.
- For a symmetrical markov process ⇒ $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}} $ ⇒ $p_{\text{A}} = p_{\text{B}} = 1/2$ this is the result for this first summand $H_1 = 1 \hspace{0.1cm} \rm bit/symbol$.
- The second summand $H_{\text{M}}$ must be calculated according to the second of the two upper equations.
- For a symmetrical Markov process you get $H_{\text{M}} = H_{\text{bin}}(p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B})$.
Now, this result is extended to the $k$-th entropy approximation. Here, the advantage of Markov sources over other sources is taken advantage of, that the entropy calculation for $k$-tuples is very simple. For each Markov source, the following applies
- $$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M}\big ] \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_2 = {1}/{2} \cdot \big [ H_{\rm 1} + H_{\rm M} \big ]\hspace{0.05cm}, \hspace{0.3cm} H_3 ={1}/{3} \cdot \big [ H_{\rm 1} + 2 \cdot H_{\rm M}\big ] \hspace{0.05cm},\hspace{0.3cm} H_4 = {1}/{4} \cdot \big [ H_{\rm 1} + 3 \cdot H_{\rm M}\big ] \hspace{0.05cm},\hspace{0.15cm}{\rm usw.}$$
$\text{Conclusion:}$ With the boundary condition for $k \to \infty$, one obtains the actual source entropy
- $$H = \lim_{k \rightarrow \infty} H_k = H_{\rm M} \hspace{0.05cm}.$$
From this simple result important insights for the entropy calculation follow:
- For Markov sources it is sufficient to determine the entropy approximations $H_1$ and $H_2$. Thus, the entropy of a Markov source is
- $$H = 2 \cdot H_2 - H_{\rm 1} \hspace{0.05cm}.$$
- Through $H_1$ and $H_2$ all further entropy approximations $H_k$ are also fixed for $k \ge 3$ :
- $$H_k = \frac{2-k}{k} \cdot H_{\rm 1} + \frac{2\cdot (k-1)}{k} \cdot H_{\rm 2} \hspace{0.05cm}.$$
However, these approximations are not very important. Mostly only the limit value $H$. For sources without markov properties the approximations $H_k$ are calculated only to be able to estimate this limit value, i.e. the actual entropy.
Notes:
- In the Exercise 1.5 the above equations are applied to the more general case of an asymmetric binary source.
- All equations on this page also apply to non-binary Markov sources $(M > 2)$ as shown on the next page.
Non-binary Markov sources
The following equations apply to each Markov source regardless of the symbol range:
- $$H = 2 \cdot H_2 - H_{\rm 1} \hspace{0.05cm},$$
- $$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M}\big ] \hspace{0.05cm},$$
- $$ \lim_{k \rightarrow \infty} H_k = H \hspace{0.05cm}.$$
These equations allow the simple calculation of the entropy $H$ from the approximations $H_1$ and $H_2$.
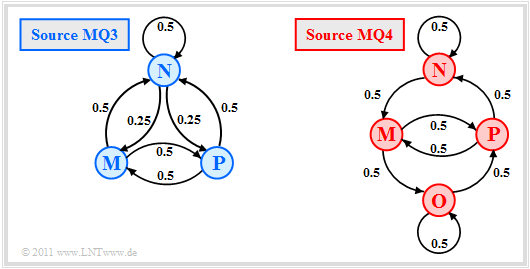
We now look at the transition diagrams sketched on the right
- a ternary Markov source $\rm MQ3$ $($ $M = 3$, blue coloring$)$ and
- a quaternary Markov source $\rm MQ4$ $(M = 4$, red color$)$.
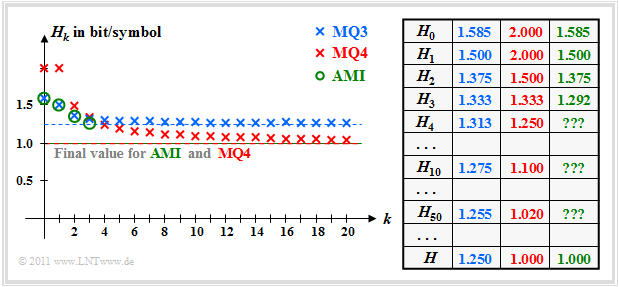
In Exercise 1.6 the entropy approximations $H_k$ and the source entropy $H$ are calculated as the limit of $H_k$ for $k \to \infty$ . The results are shown in the following figure. All entropies specified there have the unit "bit/symbol".
These results can be interpreted as follows:
- For the ternary markov source $\rm MQ3$ the entropy approximations of $H_1 = 1,500$ above $H_2 = 1,375$ up to the limit $H = 1,250$ continuously decreasing paths $M = 3$ the decision content is $H_0 = 1,585$.
- For the quaternary Markov source $\rm MQ4$ one receives $H_0 = H_1 = 2,000$ (since four equally probable states) and $H_2 = 1.5$. From the $H_1$- and $H_2$-value all entropy approximations $H_k$ and the final value $H = 1.000$ can be calculated.
- The two models $\rm MQ3$ and $\rm MQ4$ were created during the attempt to calculate the AMI-Code to be described information theoretically by Markov sources. The symbols $\rm M$, $\rm N$ and $\rm P$ stand for "minus", "zero" and "plus".
- The entropy approximations $H_1$, $H_2$ and $H_3$ of the AMI code (green markers) were calculated in the Exercise 1.4 on the calculation of $H_4$, $H_5$, ... had to be omitted for reasons of effort. But the final value of $H_k$ for $k \to \infty$ ⇒ $H = 1,000$ is known.
- You can see that the Markov model $\rm MQ3$ for $H_0 = 1,585$, $H_1 = 1,500$ and $H_2 = 1,375$ yields exactly the same numerical values as the AMI code. On the other hand $H_3$ ⇒ $(1,333$ instead of $1,292)$ and especially the final value $H$ ⇒ $(1,250$ compared to $1,000)$.
- The model $\rm MQ4$ $(M = 4)$ differs from the AMI code $(M = 3)$ with respect to the decision content $H_0$ and also with respect to all entropy approximations $H_k$. Nevertheless, $\rm MQ4$ is the more suitable model for the AMI code, since the final value $H = 1,000$ is the same.
- The model $\rm MQ3$ yields entropy values that are too large, since the sequences $\rm PNP$ and $\rm MNM$ are possible here, which cannot occur in the AMI code. Already with the approximation $H_3$ the difference is slightly noticeable, in the final value $H$ even clearly $(1.25$ instead of $1)$.
In the model $\rm MQ4$ the state "Null" was split into two states $\rm N$ and $\rm O$ (see upper right figure on this page):
- Here applies to the state $\rm N$: The current binary symbol $\rm L$ is displayed with the amplitude value $0$ (zero), as per the AMI rule. The next occurring $\rm H$ symbol, on the other hand, is displayed as $-1$ (minus), because the last $\rm H$ symbol was encoded as $+1$ (plus).
- The current binary symbol $\rm O$ is also displayed with the state $\rm L$ with the ternary value $0$ . In contrast to the state $\rm N$ however, the next occurring $\rm H$ symbol is now displayed as $+1$ (Plus) since the last $\rm H$ symbol was encoded as $-1$ (Minus).
$\text{Conclusion:}$
- The $\rm MQ4$–Output sequence actually follows the rules of the AMI code and assigns the entropy $H = 1.000 \hspace{0.15cm} \rm bit/symbol$ up.
- Because of the new state $\rm O$ but is now $H_0 = 2.000 \hspace{0.15cm} \rm bit/symbol$ $($against $1.585 \hspace{0.15cm} \rm bit/symbol)$ clearly too large.
- Also all $H_k$ approximations are larger than in AMI code.
- First for $k \to \infty$ the model $\rm MQ4$ and the AMI code match exactly: $H = 1,000 \hspace{0.15cm} \rm bit/symbol$.
Exercises for the chapter
Aufgabe 1.3: Entropienäherungen
Aufgabe 1.4: Entropienäherungen für den AMI-Code
Zusatzaufgabe 1.4Z: Entropie der AMI-Codierung
Aufgabe 1.5: Binäre Markovquelle
Aufgabe 1.5Z: Symmetrische Markovquelle
Aufgabe 1.6: Nichtbinäre Markovquellen
Aufgabe 1.6Z:Ternäre Markovquelle