Difference between revisions of "Linear and Time Invariant Systems/Some Low-Pass Functions in Systems Theory"
| Line 147: | Line 147: | ||
\hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad | \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad | ||
\begin{array}{*{10}c} {\rm{f\ddot{u}r}} | \begin{array}{*{10}c} {\rm{f\ddot{u}r}} | ||
| − | \\ {\rm{ | + | \\ {\rm{for\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} |
{\hspace{1cm} \left| \hspace{0.005cm}f\hspace{0.05cm} \right| \le {\rm \Delta}f ,} \\ | {\hspace{1cm} \left| \hspace{0.005cm}f\hspace{0.05cm} \right| \le {\rm \Delta}f ,} \\ | ||
| − | {\hspace{1cm}\left|\hspace{0.005cm} | + | {\hspace{1cm}\left|\hspace{0.005cm} f \hspace{0.05cm} \right| \ge {\rm \Delta}f } \\ |
\end{array}, \hspace{1cm} | \end{array}, \hspace{1cm} | ||
h(t) = \Delta f \cdot {\rm si}^2(\pi \cdot \Delta f \cdot t )\hspace{0.4cm}{\rm{where}}\hspace{0.4cm}{\rm si}(x) = \frac{\sin(x)}{x}.$$ | h(t) = \Delta f \cdot {\rm si}^2(\pi \cdot \Delta f \cdot t )\hspace{0.4cm}{\rm{where}}\hspace{0.4cm}{\rm si}(x) = \frac{\sin(x)}{x}.$$ | ||
Revision as of 08:54, 8 May 2021
Contents
General Remarks
All low-pass functions described on the next pages have the following properties:
- The frequency response $H(f)$ ist real and even, so that according to the Zuordnungssatz the associated impulse response$h(t)$ is always real and even, too.
- Thus, it is obvious that the systems considered here are noncausal and hence not realisable. The description of causal systems is given in the chapter Beschreibung kausaler realisierbarer Systeme of this book.
- The advantage of these systemtheoretic filter functions is the simple description by at most two parameters such that the filter influx can be represented in a transparent way.
- The most important function parameter is the equivalent bandwidth according to the definition via the rectangle of area equal to the square:
- $$\Delta f = \frac{1}{H(f=0)}\cdot \int_{-\infty}^{+\infty}H(f) \hspace{0.15cm} {\rm d}f.$$
- According to the so-called Reziprozitätsgesetz the equivalent time period of the impulse response is thus also fixed, which is also defined via the rectangle of area equal to the square:
- $$\Delta t = \frac{1}{h(t=0)}\cdot \int_{-\infty}^{+\infty}h(t) \hspace{0.15cm} {\rm d}t = \frac{1}{\Delta f}.$$
- The direct signal transmission factor wiris always assumed to be $H(f = 0) = 1$ unless explicitly stated otherwise.
- From every low-pass function corresponding high-pass functions can be derived as shown on the page Herleitung systemtheoretischer Hochpassfunktionen.
Ideal Low-Pass Filter – Küpfmüller Low-Pass Filter
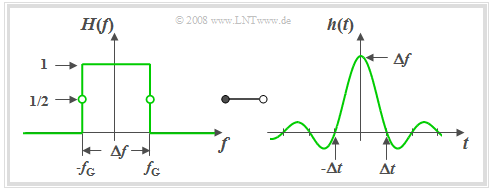
$\text{Definition:}$ An ideal low-pass filter is on hand if its frequency response is as follows:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ 0.5 \\\hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad\begin{array}{*{10}c} \text {for} \\ \text {for} \\ \text {for} \\ \end{array}\begin{array}{*{20}c}{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert< \Delta f/2,} \\{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert = \Delta f/2,} \\{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert > \Delta f/2.} \\\end{array}$$
We sometimes also use the term "Küpfmüller-low-pass filter” (KLP) in in memory of the pioneer of systems theory, Karl Küpfmüller.
The graph shows such an ideal low-pass filter in the frequency and time domain. The following can be concluded from this curve shape:
- Due to the abrupt, infinitely steep roll-off the 3dB cut-off frequency $f_{\rm G}$ is here exactly half the system-theoretical bandwidth $Δf$.
- All spectral components with $f \lt f_{\rm G}$ are transmitted undistorted (pass band).
- All components with $f \gt f_{\rm G}$ are completely suppressed (cut-off region).
- By definition, $H(f) = 0.5$ holds for $f = f_{\rm G}$.
Description of the ideal low-pass filter in the time domain:
- According to the inverse Fourier transformation the impulse response (see diagram on the right) is
- $$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t)\hspace{0.7cm}{\rm{with}}\hspace{0.7cm}{\rm si}(x) ={\sin(x)}/{x}.$$
- The impulse response $h(t)$ extended to infinity on both sides exhibits equidistant zero-crossings at an interval of $Δt = 1/ Δf$.
- The asymptotic decay is inversely proportional to time:
- $$|h(t)| = \frac{\Delta f}{\pi \cdot \Delta f \cdot |t|} \cdot \left |{\rm sin}(\pi \cdot \Delta f\cdot t )\right | \le \frac{1}{\pi \cdot |t|}.$$
- It follows that the impulse response is certainly less than $1‰$ of the impulse maximum only for times $t \gt t_{1‰} = 318 \cdot \Delta t$ .
- The step response $\sigma(t)$ is obtained from the impulse response by integration and is:
- $${\sigma}(t) = \int_{ - \infty }^{ t } {h ( \tau )} \hspace{0.1cm}{\rm d}\tau = \frac{1}{2} + \frac{1}{\pi} \cdot {\rm Si}(\pi \cdot\Delta f \cdot t ).$$
- Here the so-called integral sine function is used:
- $${\rm Si}(x) = \int_{ 0 }^{ x } {{\rm si} ( \xi )} \hspace{0.1cm}{\rm d}\xi = x - \frac{x^3}{3 \cdot 3!} + \frac{x^5}{5 \cdot 5!} - \frac{x^7}{7 \cdot 7!}+\text{ ...}$$
- It has the following properties:
- $${\rm Si}(0) = 0, \hspace{0.3cm}{\rm Si}(\infty) = \frac{\pi}{2}, \hspace{0.3cm}{\rm Si}(-x) = -{\rm Si}(x).$$
Note: In some books, instead of the function ${\rm si}(x)$ the similar function ${\rm sinc}(x)$ is used:
- $${\rm si}(x) = \frac{\sin(x)}{x}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}{\rm sinc}(x) = \frac{\sin(\pi x)}{\pi x} = {\rm si}(\pi x).$$
Thus, the impulse response of the ideal low-pass filter is: $h(t)$ = $Δf · {\rm sinc}(Δf · t).$
Slit Low-Pass Filter
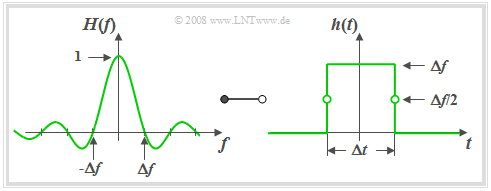
$\text{Definition:}$ An LTI–system is called a slit–low-pass filter if the frequency response has the following form:
- $$H(f) = {\rm si}(\pi {f}/{ \Delta f})\hspace{0.7cm}{\rm{where} }\hspace{0.7cm}{\rm si}(x) ={\sin(x)}/{x}.$$
From the graph on the left it can be seen that the frequency response $H_{\rm SLP}(f)$ of the slit–low-pass is identical in shape to the impulse response $h_{\rm KLP}(t)$ of the Küpfmüller-low-pass.
According to the Vertauschungssatz the impulse response $h_{\rm SLP}(t)$ of the slit low-pass filter must also have the same form as the frequency response $H_{\rm KLP}(f)$ of the ideal low-pass filter.
Thus, with $Δt = 1/ Δf$ the following holds:
- $$h(t) = \left\{ \begin{array}{l} \hspace{0.25cm}\Delta f \\ \Delta f/2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} \text{for} \\ \text{for} \\ \text{for} \\ \end{array}\begin{array}{*{20}c} {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert < \Delta t/2,} \\ {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert = \Delta t/2,} \\ {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert > \Delta t/2.} \\ \end{array}$$
Based on the graph on the right the following statements can be derived:
- The slit–low-pass filter is also noncausal in this form.
- However, adding a running time of $Δt/2$ renders the system causal and thus realisable.
- The slit–low-pass filter acts as an integrator over the time period $Δt$:
- $$y(t) = x (t) * h (t) = \frac{1}{\Delta t} \cdot \int\limits_{ t - \Delta t/2 }^{ t + \Delta t/2 } {x ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$
- If $x(t)$ is a harmonic oscillation with frequency $f_0 = k \cdot Δf$ (where $k$ is an integer), then it integrates exactly over $k$ periods and $y(t) = 0$ holds. This is also shown by the zeros of $H(f)$.
Gaussian Low-Pass Filter
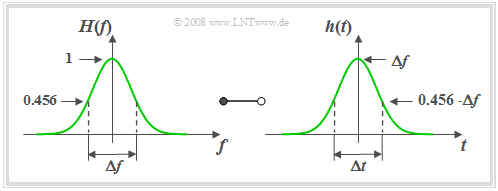
A filter function frequently used for system-theoretical investigations is the Gaussian low-pass filter, which can also be described by only one parameter, namely the äquivalente Bandbreite $Δf$.
$\text{Definition:}$ For the frequency response and impulse response of the Gaussian low-pass filter the following holds:
- $$H(f) = {\rm e}^{-\pi(f/\Delta f)^2}\hspace{0.15cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.15cm}h(t) = \Delta f \cdot {\rm e}^{-\pi(\Delta f \cdot \hspace{0.03cm} t)^2} .$$
The name goes back to the mathematician, physicist and astronomer Carl-Friedrich Gauß. Gauss did not deal with this subject matter himself, but the mathematical form of the frequency response and impulse response bear a resemblance to the so-calledGaußformel which he discovered for probability theory.
Based on this graph the following statements can be made:
- The äquivalente Impulsdauer $Δt$ is also defined via the rectangle of area equal to the square and is equal to the reciprocal of the equivalent bandwith $Δf$.
- A narrow-band filter function (small $Δf$) results in a wide (large $Δt$) and simultaneously low impulse response $h(t)$.
- The so-called Reziprozitätsgesetz of time period and bandwidth can be shown particularly clearly in the example of the Gaussian low-pass filter.
- The frequency and time domain representations are in principle of the same form. The Gaussian function is also said to be invariant to the Fourier transformation.
- The Gaussian low-pass filter is - like the ideal low-pass filter - strongly noncausal and (exactly) realisable only with infinitely large transit time due to the infinite propagation of its impulse response.
- However, it must be taken into account that $h(t)$ has already decayed to $1‰$ of its maximum value at $t = 1.5 \cdot Δt$ . For $t = 3 \cdot Δt$ we even get $h(t) ≈ 5 · 10^{–13} · h(0)$.
- These numerical values show that the Gaussian low-pass filter can be used feasibly for practical simulations as long as runtimes do not play a system-limiting role.
- The step response $σ(t)$ is given for the Gaussian error function $ϕ(x)$, which is usually given in formularies:
- $$\sigma(t) = \int_{ -\infty }^{ t } {h(\tau)} \hspace{0.1cm}{\rm d}\tau = {\rm \phi}\left( \sqrt{2 \pi }\cdot{t}/{\Delta t} \right) \hspace{0.7cm}{\rm{where}}\hspace{0.7cm}{\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot \int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$
Trapezoid Low-Pass Filter
The low-pass functions described so far in this chapter depend on only one parameter - the equivalent bandwidth $Δf$. Here, the edge steepness for a given filter type was fixed.
Now a low-pass filter with parameterisable edge steepness is described.
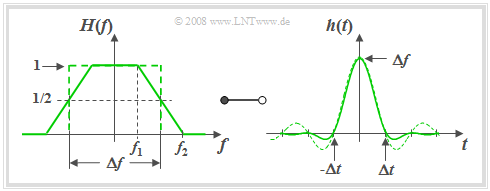
$\text{Definition:}$ The frequency response of the trapezoid low-pass filter with cut-off frequencies $f_1$ and $f_2 \ge f_1$:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \frac{f_2 - \vert f \vert }{f_2 -f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} \text{for} \\ \text{for} \\ \text{for} \\ \end{array}\begin{array}{*{20}c} {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert < f_1,} \\ {f_1 \le \vert \hspace{0.005cm} f\hspace{0.05cm} \vert \le f_2,} \\ {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert > f_2.} \\ \end{array}$$
Instead of $f_1$ and $f_2$ the following parameters can be used to describe $H(f)$:
- the equivalent bandwidth determined via the rectangle of area equal to the square:
- $$\Delta f = f_1 + f_2.$$
- the roll-off factor (in the frequency domain) as a measure for the edge steepness:
- $$r_{\hspace{-0.05cm}f} = \frac{f_2 - f_1}{f_2 + f_1}.$$
Special cases included in the general representation are:
- the ideal rectangular low-pass filter $(r_{\hspace{-0.05cm}f} = 0)$,
- the triangular low-pass filter $(r_{\hspace{-0.05cm}f} = 1)$.
For a roll-off factor of $r_f = 0.5 \ \Rightarrow \ f_2 = 3f_1$ the following graph shows the frequency response $H(f)$ on the left and the impulse response
- $$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t )\cdot {\rm si}(\pi \cdot r_{\hspace{-0.05cm}f} \cdot \Delta f \cdot t )\hspace{0.7cm}{\rm{where}}\hspace{0.7cm}{\rm si}(x) = {\sin(x)}/{x}$$ on the right.
The time-dependent $\rm si$–curve of the rectangular low-pass filter with the same equivalent bandwidth is shown dashed for comparison.
With the help of the graph and the above equations the following statements can be made:
- The trapezoidal shape is obtained, for example, by convolution of two rectangles of widths $Δf$ and $r_f \cdot Δf$.
- According to the convolution theorem the impulse response is thus the product of two $\rm si$–functions with arguments $π · Δf · t$ and $π · r_{\hspace{-0.05cm}f} · Δf · t$.
- The first $\rm si$–function is part of the equation for $h(t)$ for all values of $r_{\hspace{-0.05cm}f}$ and always results in equivalent zero-crossings at an interval of $1/Δf$.
- For $0 \lt r_{\hspace{-0.05cm}f} \lt 1$ there are further zero-crossings at multiples of $Δt/r_{\hspace{-0.05cm}f}$.
- The larger $r_{\hspace{-0.05cm}f}$ is (i.e. for a given $Δf$ with a flatter edge), the faster is the asymptotic decay of the impulse response $h(t)$.
- The fastest possible decay is obtained for the triangular low-pass filter ⇒ $r_{\hspace{-0.05cm}f} = 1$, $f_1 = 0$, $f_2 = Δf$. For this, the following holds in the frequency and time domains:
- $$H(f) = \left\{ \begin{array}{c} \hspace{0.25cm} \frac{{\rm \Delta}f -|f|}{{\rm \Delta}f} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{for\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\hspace{1cm} \left| \hspace{0.005cm}f\hspace{0.05cm} \right| \le {\rm \Delta}f ,} \\ {\hspace{1cm}\left|\hspace{0.005cm} f \hspace{0.05cm} \right| \ge {\rm \Delta}f } \\ \end{array}, \hspace{1cm} h(t) = \Delta f \cdot {\rm si}^2(\pi \cdot \Delta f \cdot t )\hspace{0.4cm}{\rm{where}}\hspace{0.4cm}{\rm si}(x) = \frac{\sin(x)}{x}.$$
Raised-Cosine Low-Pass Filter
Ebenso wie der Trapez–Tiefpass wird dieser Tiefpass durch zwei Parameter beschrieben, nämlich durch
- die äquivalente Bandbreite $Δf$ und
- den Rolloff–Faktor $r_{\hspace{-0.05cm}f}$.
Dessen Wertebereich liegt zwischen $r_{\hspace{-0.05cm}f} = 0$ (Rechtecktiefpass) und $r_{\hspace{-0.05cm}f} = 1$ (Cosinus–Quadrat–Tiefpass).
$\text{Definition:}$ Mit den Eckfrequenzen $f_1 = Δf · (1 – r_{\hspace{-0.05cm}f})$ und $f_2 = Δf · (1 + r_{\hspace{-0.05cm}f})$ lautet der Frequenzgang des Cosinus–Rolloff–Tiefpasses:
- $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \cos \left( \frac{ \vert f \vert - f_1}{f_2 -f_1}\frac{\pi}{2}\right) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} \text{for} \\ \text{for} \\ \text{for} \\ \end{array}\begin{array}{*{20}c} {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert < f_1,} \\ {f_1 \le \vert \hspace{0.005cm} f\hspace{0.05cm} \vert \le f_2,} \\ {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert> f_2.} \\ \end{array}$$
Die Grafik zeigt links $H(f)$ sowie rechts die Impulsantwort
- $$h(t) = \Delta f \hspace{-0.05cm}\cdot\hspace{-0.05cm} {\rm si}(\pi \hspace{-0.05cm}\cdot\hspace{-0.05cm} \Delta f \hspace{-0.05cm}\cdot\hspace{-0.05cm} t )\hspace{-0.05cm}\cdot\hspace{-0.05cm} \frac {\cos(\pi \cdot r_{\hspace{-0.05cm}f} \cdot \Delta f \cdot t )}{1 - (2 \cdot r_f \cdot \Delta f \cdot t)^2}.$$
Für diese Grafiken wurde der Rolloff–Faktor $r_{\hspace{-0.05cm}f} = 0.5$ verwendet, das heißt, es gilt $f_2 = 3 \cdot f_1$.
Gestrichelt sind zum Vergleich eingezeichnet:
- im Frequenzbereich der Trapeztiefpass und
- im Zeitbereich die $\rm si$–Funktion.
Es ist zu beachten:
- Die $\rm si$–Funktion ist nicht die Fourierrücktransformierte des links blau eingezeichneten Trapeztiefpasses.
- Sie beschreibt vielmehr den (nicht dargestellten) idealen, rechteckförmigen Tiefpass im Zeitbereich.
Anhand dieser Grafik und den obigen Gleichungen sind folgende Aussagen möglich:
- Die Impulsantwort $h(t)$ des Cosinus–Rolloff–Tiefpasses hat bei allen Vielfachen von $Δt = 1/Δf$ Nullstellen, die auf die im rechten Bild gestrichelt eingezeichnete si–Funktion zurückzuführen sind.
- Der letzte Term in der $h(t)$–Gleichung führt zu weiteren Nullstellen bei Vielfachen von $Δt/r_f$. Ist $1/r_f$ ganzzahlig wie in obiger Grafik $(1/r_f = 2)$, so fallen diese neuen Nullstellen mit den anderen Nullstellen zusammen, sind also nicht erkennbar.
- Je größer der Rolloff-Faktor $r_f$ ist und je flacher damit der Flankenabfall erfolgt, desto günstiger ist im Allgemeinen das Einschwingverhalten des Cosinus-Rolloff-Tiefpasses.
- Der Cosinus–Rolloff–Tiefpass zeigt meist ein besseres asymptotisches Einschwingverhalten als der Trapez–Tiefpass mit gleichem $r_f$, obwohl dieser zumindest bei $Δf/2$ eine flachere Flanke aufweist.
- Dies lässt darauf schließen, dass das Einschwingverhalten nicht nur durch Unstetigkeitsstellen (wie beim Rechteck), sondern auch durch Knickpunkte wie beim Trapez–Tiefpass beeinträchtigt wird.
$\text{Definition:}$ Als Sonderfall ergibt sich mit $f_1 = 0$, $f_2 = Δf$ ⇒ $r_f = 1$ der Cosinus–Quadrat–Tiefpass, dessen Impulsantwort auch wie folgt dargestellt werden kann:
- $$h(t) = \frac{1}{ \Delta t}\cdot{\rm si}(\pi \frac{t}{ \Delta t}) \cdot \left[ {\rm si}(\pi \frac{t}{ \Delta t} + 0.5) - {\rm si}(\pi \frac{t}{ \Delta t} - 0.5) \right].$$
- Diese Funktion hat Nullstellen bei $t/Δt = ±1, ±1.5, ±2, ±2.5$ usw., nicht jedoch bei $t/Δt = ±0.5$.
- Der Cosinus–Quadrat–Tiefpass erfüllt als einziger Tiefpass beide Nyquistkriterien ⇒ siehe Buch Digital Signal Transmission.
Herleitung systemtheoretischer Hochpassfunktionen
Bisher wurden in diesem Kapitel fünf häufig verwendete systemtheoretische Tiefpassfunktionen betrachtet. Für jede einzelne Tiefpassfunktion lässt sich auch eine äquivalente Hochpassfunktion angeben.
$\text{Definition:}$ Ist $H_{\rm TP}(f)$ eine systemtheoretische TP–Funktion mit $H_{\rm TP}(f = 0) = 1$, so ist die äquivalente Hochpassfunktion:
- $$H_{\rm HP}(f) = 1 - H_{\rm TP}(f).$$
Damit lauten die Beschreibungsgrößen im Zeitbereich:
- $$h_{\rm HP}(t) = \delta (t) - h_{\rm TP}(t),\hspace{1cm} \sigma_{\rm HP}(t) = \gamma (t) - \sigma_{\rm TP}(t). $$
Hierbei bezeichnen:
- $h_{\rm HP}(t)$ und $h_{\rm TP}(t)$ die Impulsantworten von Hoch– und Tiefpass,
- $σ_{\rm HP}(t)$ und $σ_{\rm TP}(t)$ die dazugehörigen Sprungantworten,
- $γ(t)$ die Sprungfunktion als Ergebnis der Integration über die Diracfunktion $δ(t)$.
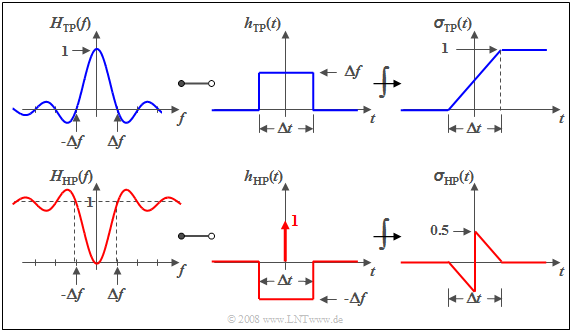
$\text{Beispiel 1:}$ Wir betrachten den Spalttiefpass, der sich durch einen $\rm si$–förmigen Frequenzgang, eine rechteckförmige Impulsantwort und eine linear ansteigende Sprungantwort auszeichnet. Diese sind in der nachfolgenden Grafik dargestellt.
Die untere Skizze zeigt die entsprechenden Hochpassfunktionen.
Man erkennt, dass
- $H_{\rm HP}(f = 0)$ immer den Wert $0$ besitzt, wenn $H_{\rm TP}(f = 0) = 1$ ist,
- demzufolge das Integral über $h_{\rm HP}(t)$ ebenfalls Null ergeben muss, und
- auch die Sprungantwort $σ_{\rm HP}(t)$ gegen den Endwert Null tendiert.
Exercises for the Chapter
Aufgabe 1.5: Idealer rechteckförmiger Tiefpass
Aufgabe 1.5Z: si-förmige Impulsantwort
Aufgabe 1.6: Rechtförmeckige Impulsantwort
Aufgabe 1.6Z: Interpretation der Übertragungsfunktion
Aufgabe 1.7: Nahezu kausaler Gaußtiefpass
Aufgabe 1.8: Variable Flankensteilheit
Aufgabe 1.8Z: Cosinus-Quadrat-Tiefpass