Difference between revisions of "Linear and Time Invariant Systems/System Description in Time Domain"
| (79 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Basics of System Theory |
| − | |Vorherige Seite= | + | |Vorherige Seite=System Description in Frequency Domain |
| − | |Nächste Seite= | + | |Nächste Seite=Some Low-Pass Functions in System Theory |
}} | }} | ||
| − | == | + | ==Impulse response== |
<br> | <br> | ||
| − | + | In the section [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|»The first Fourier integral«]] in the book »Signal Representation» it was explained that for any deterministic signal $x(t)$ a »spectral function« $X(f)$ can be given with the help of the Fourier transform. Often $X(f)$ is referred to as the »spectrum« for short. | |
| − | + | However, all information about the spectral function is already contained in the time domain representation, even if not always immediately recognizable. The same facts apply to linear time-invariant systems. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | The most important descriptive quantity of a linear time-invariant system in the time domain is the inverse Fourier transform of $H(f)$, which is called the »'''impulse response'''«: | |
:$$h(t) = \int_{-\infty}^{+\infty}H(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}2\pi ft}\hspace{0.15cm} {\rm d}f.$$}} | :$$h(t) = \int_{-\infty}^{+\infty}H(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}2\pi ft}\hspace{0.15cm} {\rm d}f.$$}} | ||
| − | + | The following should be noted in this regard: | |
| − | * | + | *The frequency response $H(f)$ and the impulse response $h(t)$ are equivalent descriptive quantities that contain exactly the same information about the LTI system. |
| − | * | + | *If the Dirac-shaped input signal $x(t) = δ(t)$ is used, then $X(f) = 1$ is to be set and $Y(f) = H(f)$ resp. $y(t) = h(t)$ are valid. |
| − | * | + | *The term »impulse response« reflects this statement: $h(t)$ is the response of the system to a $($Dirac delta$)$ function as the input signal. |
| − | * | + | *The above definition suggests that any impulse response must have the unit $\text{Hz = 1/s}$. |
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ |
| − | + | The impulse response $h(t)$ of the so-called »rectangular–in–time« filter is constant over a time interval $T$ and is zero outside this time interval. | |
| − | * | + | [[File:P_ID837__LZI_T_1_2_S1_neu.png|right|frame|Rectangular impulse response and associated magnitude spectrum|class=fit]] |
| − | :$$\vert H(f)\vert = \vert {\rm si}(\pi fT)\vert .$$ | + | *The associated amplitude response as the magnitude of the frequency response is |
| − | * | + | :$$\vert H(f)\vert = \vert {\rm si}(\pi fT)\vert \hspace{0.5cm}\text{with}\hspace{0.5cm}{\rm si}(x)=\sin(x)/x={\rm sinc}(x/\pi).$$ |
| − | * | + | *The area over $h(t)$ is equal to $H(f = 0) = 1$. It follows that: <br> In the range $ 0 < t < T$ the impulse response must be constant and equal to $1/T$. |
| − | :$$b(f) = \left\{ \begin{array}{l} \hspace{0.25cm}\pi/T \\ - \pi/T \\ \end{array} \right.\quad \quad\begin{array}{*{20}c} \text{ | + | *The phase response is given by |
| − | * | + | :$$b(f) = \left\{ \begin{array}{l} \hspace{0.25cm}\pi/T \\ - \pi/T \\ \end{array} \right.\quad \quad\begin{array}{*{20}c} \text{for} \\ \text{for} \\ \end{array}\begin{array}{*{20}c}{\left \vert \hspace{0.05cm} f\hspace{0.05cm} \right \vert > 0,} \\{\vert \hspace{0.05cm} f \hspace{0.05cm} \vert < 0.} \\\end{array}$$ |
| + | *With symmetrical $h(t)$ around $t = 0$ $($i.e. non-causal$)$ ⇒ $b(f)=0$. }} | ||
| − | == | + | ==Some laws of the Fourier transform== |
<br> | <br> | ||
| − | + | The [[Signal_Representation/Fourier_Transform_Theorems|'''»Fourier transform theorems«''']] have already been explained in detail in the book »Signal Representation«. | |
| − | + | The following is a short summary, where $H(f)$ describes the frequency response of an LTI system and whose inverse Fourier transform $h(t)$ is the impulse response. The laws and principles are applied more frequently in the [[Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain#Exercises_for_the_chapter|»$\text{exercises}$«]] for this chapter »System Description in Time Domain«. | |
| − | + | Here, we also refer to the (German language) didactic video [[Gesetzmäßigkeiten_der_Fouriertransformation_(Lernvideo)|"Gesetzmäßigkeiten der Fouriertransformation"]] ⇒ "Regularities to the Fourier transform". | |
| − | + | In the following equations the short symbol of the Fourier transformation is used. The filled-out circle indicates the spectral domain, the white one the time domain. | |
| − | *''' | + | *»'''Multiplication'''« by a constant factor: |
:$$k \cdot H(f)\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,k \cdot h(t).$$ | :$$k \cdot H(f)\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,k \cdot h(t).$$ | ||
| − | : | + | ::For $k \lt 1$ one deals with attenuation, while $k \gt 1$ stands for amplification. |
| − | *''' | + | *»'''Similarity Theorem'''«: |
:$$H({f}/{k})\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,|k| \cdot h(k\cdot t).$$ | :$$H({f}/{k})\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,|k| \cdot h(k\cdot t).$$ | ||
| − | :# | + | :# This implies: Compression $(k < 1)$ of the frequency response results in a wider and lower impulse response. |
| − | :# | + | :# Stretching $(k > 1)$ of $H(f)$ makes $h(t)$ narrower and higher. |
| − | *''' | + | *»'''Displacement Theorem'''« in the frequency and time domain: |
| − | :$$H(f - f_0) \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, h( t )\cdot {\rm e}^{\hspace{0.05cm}{\rm j}2\pi f_0 t}, | + | :$$H(f - f_0) \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, h( t )\cdot {\rm e}^{\hspace{0.05cm}{\rm j}2\pi f_0 t},$$ |
| − | H(f) \cdot {\rm e}^{-{\rm j}2\pi ft_0}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, h( t- t_0 ).$$ | + | :$$H(f) \cdot {\rm e}^{-{\rm j}2\pi ft_0}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, h( t- t_0 ).$$ |
| − | :# | + | :# A shift by $t_0$ $($»transit time»$)$ thus leads to multiplication by a complex exponential function in the frequency domain. |
| − | :# | + | :# Thereby, the amplitude response $|H(f)|$ does not change. |
| − | *''' | + | *»'''Differentiation Theorem'''« in the frequency and time domain: |
| − | :$$\frac{1}{{{\rm j}2\pi }} \cdot \frac{{{\rm d}H( f )}}{{{\rm d}f}} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,- t \cdot h( t ), | + | :$$\frac{1}{{{\rm j}2\pi }} \cdot \frac{{{\rm d}H( f )}}{{{\rm d}f}} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,- t \cdot h( t ),$$ |
| − | {\rm j}\cdot 2\pi f \cdot H( f ){}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \frac{{{\rm d}h( t )}}{{\rm d}t}.$$ | + | :$${\rm j}\cdot 2\pi f \cdot H( f ){}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \frac{{{\rm d}h( t )}}{{\rm d}t}.$$ |
| − | : | + | :# A differentiating element in the LTI system leads to a multiplication by ${\rm j}\cdot 2πf$ in the frequency domain |
| + | :# and thus among other things to a phase rotation by $90^{\circ}$. | ||
| − | == | + | ==Causal systems== |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | An LTI system is said to be $\text{causal}$ if the impulse response $h(t)$ – that is the inverse Fourier transform of the frequency response $H(f)$ – satisfies the following condition: | |
| − | :$$h(t) = 0 \hspace{0.25cm}{\rm | + | :$$h(t) = 0 \hspace{0.25cm}{\rm for}\hspace{0.25cm} t < 0.$$ |
| − | $\text{ | + | |
| + | If this condition is not met, the system is »'''non–causal'''« $($or »acausal«$)$. | ||
| + | |||
| + | $\text{Please note:}$ Any realizable system is causal. }} | ||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ |
| − | + | The diagram illustrates the differences between the non–causal system $\rm A$ and the causal system $\rm B$. | |
| − | * | + | [[File:P_ID806__LZI_T_1_2_S3_neu.png|right|frame|Non–causal system $\rm A$ and causal system $\rm B$|class=fit]] |
| − | * | + | *In system $\rm A$ the effect starts earlier $($at $t =\hspace{0.05cm} –T)$ than the cause $($Dirac delta function at $t = 0)$, which of course is not possible in practice. |
| − | * | + | |
| − | + | *Almost all non–causal systems can be transformed into a feasible causal system using a transit time $\tau$. | |
| + | |||
| + | *For example, with $\tau = T$ the following holds: $h_{\rm B}(t) = h_{\rm A}(t - T).$ | ||
| + | |||
| + | All statements made so far apply for causal as well as non–causal systems. | ||
| − | + | ||
| − | + | However, for the description of causal systems some specific properties can be used as explained in the third main chapter »Description of Causal Realizable Systems« of [[Lineare_zeitinvariante_Systeme|$\text{this book}$]].}} | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | In | + | In this first and the following second main chapter we mainly consider non–causal systems since their mathematical description is usually simpler. |
| − | *So | + | *So in this example, the frequency response $H_{\rm A}(f)$ is real, |
| − | * | + | |
| + | *while for $H_{\rm B}(f)$ the additional term ${\rm e}^{–{\rm j2π}f\hspace{0.05cm}T}$ has to be considered. }} | ||
| − | == | + | ==Computation of the output signal== |
<br> | <br> | ||
| − | + | We consider the following problem: Let the input signal $x(t)$ and the frequency response $H(f)$ be known. The output signal $y(t)$ is to be determined. | |
| − | [[File:EN_LZI_T_1_2_S4.png|right|frame| | + | [[File:EN_LZI_T_1_2_S4.png|right|frame|To determine the output quantities of an LTI system|class=fit]] |
| − | + | If the solution is to be determined in the frequency domain, first the spectrum $X(f)$ must be determined from the given input signal $x(t)$ via [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|$\text{Fourier transform}$]] and multiplied by the frequency response $H(f)$. By the [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_second_Fourier_integral|$\text{inverse Fourier transform}$]] of the product the signal $y(t)$ is obtained. | |
| − | + | Here is a summary of the entire solution process: | |
| − | :$${\rm 1.\,\, | + | :$${\rm 1.\,\, step\hspace{-0.1cm} :}\hspace{0.5cm} X(f)\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, x( t )\hspace{1.55cm}{\rm input\:spectrum},$$ |
| − | :$${\rm 2.\,\, | + | :$${\rm 2.\,\, step\hspace{-0.1cm}:}\hspace{0.5cm}Y(f)= X(f) \cdot H(f) \hspace{0.82cm}{\rm output\:spectrum},$$ |
| − | :$${\rm 3.\,\, | + | :$${\rm 3.\,\, step\hspace{-0.1cm}:}\hspace{0.5cm} y(t)\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, Y(f )\hspace{1.55cm}{\rm output\:signal}.$$ |
| − | + | The same result is obtained after the computation in the time domain by first determining the impulse response $h(t)$ from the frequency response $H(f)$ by means of the »inverse Forier transform« and then applying the convolution operation: | |
:$$y(t) = x (t) * h (t) = \int_{ - \infty }^{ + \infty } {x ( \tau )} \cdot h ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | :$$y(t) = x (t) * h (t) = \int_{ - \infty }^{ + \infty } {x ( \tau )} \cdot h ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | * | + | *The results are identical for both approaches. |
| − | * | + | |
| + | *Purposefully, the procedure of solution with less computational effort should be chosen. | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ |
| − | + | At the input of a filter with rectangular impulse response $h(t)$ of width $T$ $($see [[Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain#Impulse_response|$\text{Example 1)}$]] a rectangular pulse $x(t)$ of duration $2T$ is applied. | |
| − | [[File:P_ID812__LZI_T_1_2_S4b_neu.png|right|frame| | + | [[File:P_ID812__LZI_T_1_2_S4b_neu.png|right|frame|Trapezoidal output signal since $x(t)$ and $h(t)$ are rectangular|class=fit]] |
| − | In | + | In this case, direct computation in the time domain is more convenient: |
| − | * | + | *The convolution of two rectangles $x(t)$ and $h(t)$ of different widths results in a trapezoidal output signal $y(t)$. |
| − | * | + | *The low-pass property of the filter can be seen from the finite edge steepness of $y(t)$. |
| − | * | + | *The pulse height $(3\text{ V)}$ is preserved in this example because of |
:$$H(f = 0) = 1/T · T = 1.$$ }} | :$$H(f = 0) = 1/T · T = 1.$$ }} | ||
| − | == | + | ==Step response== |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Definition:}$ |
| − | + | In practice, one of the often used input functions $x(t)$ in order to measure $H(f)$ is the »'''jump function'''« | |
| − | :$${\rm \gamma}(t) = \left\{ \begin{array}{l} \hspace{0.25cm}0 \\ 0.5 \\ \hspace{0.25cm} 1 \\ \end{array} \right.\quad \quad\begin{array}{*{20}c} \text{ | + | :$${\rm \gamma}(t) = \left\{ \begin{array}{l} \hspace{0.25cm}0 \\ 0.5 \\ \hspace{0.25cm} 1 \\ \end{array} \right.\quad \quad\begin{array}{*{20}c} \text{for} \\ \text{for}\\ \text{for} \\ \end{array}\begin{array}{*{20}c}{\vert \hspace{0.05cm} t\hspace{0.05cm} \vert < 0,} \\ {\vert \hspace{0.05cm}t\hspace{0.05cm} \vert = 0,} \\ {\vert \hspace{0.05cm} t \hspace{0.05cm} \vert > 0.} \\ \end{array}$$ |
| − | + | The »'''step response'''« $\sigma(t)$ is the response of the system if the jump function $\gamma(t)$ is applied to the input: | |
:$$x(t) = {\rm \gamma}(t)\hspace{0.5cm}\Rightarrow \hspace{0.5cm} y(t) = {\rm \sigma}(t).$$}} | :$$x(t) = {\rm \gamma}(t)\hspace{0.5cm}\Rightarrow \hspace{0.5cm} y(t) = {\rm \sigma}(t).$$}} | ||
| − | + | The computation in the frequency domain would be a bit laborious here because the following equation would have to be applied: | |
:$${\rm \sigma}(t)\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, X(f ) \cdot H(f) =\left({1}/{2}\cdot \delta(f) + \frac{1}{{\rm j}\cdot 2\pi f} \right) \cdot H(f).$$ | :$${\rm \sigma}(t)\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, X(f ) \cdot H(f) =\left({1}/{2}\cdot \delta(f) + \frac{1}{{\rm j}\cdot 2\pi f} \right) \cdot H(f).$$ | ||
| − | + | In contrast to this, the computation in the time domain leads directly to the result: | |
:$${\rm \sigma}(t) = \int_{ - \infty }^{ t } {h ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$ | :$${\rm \sigma}(t) = \int_{ - \infty }^{ t } {h ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | + | For causal sytems $h(\tau) = 0$ holds for $\tau \lt 0$, such that the lower limit of integration in the above equation can be set to $\tau = 0$. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Proof:}$ |
| − | + | The above result is also insightful for the following reason: | |
| − | * | + | *The jump function $\gamma(t)$ is related to the Dirac delta function $\delta(t)$ as follows: |
:$${\rm \gamma}(t) = \int_{ - \infty }^{ t } {\delta ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$ | :$${\rm \gamma}(t) = \int_{ - \infty }^{ t } {\delta ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | * | + | *Since we have assumed linearity and integration is a linear operation the corresponding relationship also applies to the output signal: |
:$${\rm \sigma}(t) = \int_{ - \infty }^{ t } {h ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$ | :$${\rm \sigma}(t) = \int_{ - \infty }^{ t } {h ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$ | ||
<div align="right">q.e.d.</div>}} | <div align="right">q.e.d.</div>}} | ||
| − | [[File:EN_LZI_T_1_2_S5.png|right|frame| | + | {{GraueBox|TEXT= |
| − | + | [[File:EN_LZI_T_1_2_S5.png|right|frame|Computation of the step response for rectangular impulse response|class=fit]] | |
| − | $\text{ | + | |
| − | + | $\text{Example 4:}$ | |
| − | * | + | The graph illustrates the facts for the rectangular impulse response $h(\tau)$. |
| − | * | + | |
| − | * | + | |
| − | * | + | $\text{Note:}$ |
| + | |||
| + | *The abscissa has been renamed to $\tau$. | ||
| + | |||
| + | *The jump function $\gamma(\tau)$ is drawn in blue. | ||
| + | |||
| + | * $\gamma(t - \tau)$ is obtained by mirroring and shifting ⇒ curve dashed in violet. | ||
| + | |||
| + | *The red shaded area thus gives the step response $\sigma(\tau)$ at time $\tau = t$ .}} | ||
| − | == | + | ==Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.3:_Measured_Step_Response|Exercise 1.3: Measured Step Response]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.3Z:_Exponentially_Decreasing_Impulse_Response|Exercise 1.3Z: Exponentially Decreasing Impulse Response]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.4:_Low-Pass_Filter_of_2nd_Order|Exercise 1.4: Low-Pass Filter of 2nd Order]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.4Z:_Everything_Rectangular|Exercise 1.4Z: Everything Rectangular]] |
{{Display}} | {{Display}} | ||
Latest revision as of 18:21, 2 November 2023
Contents
Impulse response
In the section »The first Fourier integral« in the book »Signal Representation» it was explained that for any deterministic signal $x(t)$ a »spectral function« $X(f)$ can be given with the help of the Fourier transform. Often $X(f)$ is referred to as the »spectrum« for short.
However, all information about the spectral function is already contained in the time domain representation, even if not always immediately recognizable. The same facts apply to linear time-invariant systems.
$\text{Definition:}$ The most important descriptive quantity of a linear time-invariant system in the time domain is the inverse Fourier transform of $H(f)$, which is called the »impulse response«:
- $$h(t) = \int_{-\infty}^{+\infty}H(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}2\pi ft}\hspace{0.15cm} {\rm d}f.$$
The following should be noted in this regard:
- The frequency response $H(f)$ and the impulse response $h(t)$ are equivalent descriptive quantities that contain exactly the same information about the LTI system.
- If the Dirac-shaped input signal $x(t) = δ(t)$ is used, then $X(f) = 1$ is to be set and $Y(f) = H(f)$ resp. $y(t) = h(t)$ are valid.
- The term »impulse response« reflects this statement: $h(t)$ is the response of the system to a $($Dirac delta$)$ function as the input signal.
- The above definition suggests that any impulse response must have the unit $\text{Hz = 1/s}$.
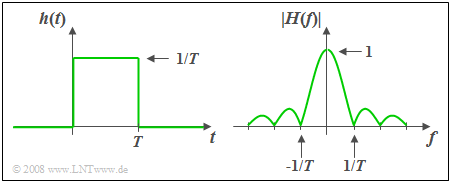
$\text{Example 1:}$ The impulse response $h(t)$ of the so-called »rectangular–in–time« filter is constant over a time interval $T$ and is zero outside this time interval.
- The associated amplitude response as the magnitude of the frequency response is
- $$\vert H(f)\vert = \vert {\rm si}(\pi fT)\vert \hspace{0.5cm}\text{with}\hspace{0.5cm}{\rm si}(x)=\sin(x)/x={\rm sinc}(x/\pi).$$
- The area over $h(t)$ is equal to $H(f = 0) = 1$. It follows that:
In the range $ 0 < t < T$ the impulse response must be constant and equal to $1/T$. - The phase response is given by
- $$b(f) = \left\{ \begin{array}{l} \hspace{0.25cm}\pi/T \\ - \pi/T \\ \end{array} \right.\quad \quad\begin{array}{*{20}c} \text{for} \\ \text{for} \\ \end{array}\begin{array}{*{20}c}{\left \vert \hspace{0.05cm} f\hspace{0.05cm} \right \vert > 0,} \\{\vert \hspace{0.05cm} f \hspace{0.05cm} \vert < 0.} \\\end{array}$$
- With symmetrical $h(t)$ around $t = 0$ $($i.e. non-causal$)$ ⇒ $b(f)=0$.
Some laws of the Fourier transform
The »Fourier transform theorems« have already been explained in detail in the book »Signal Representation«.
The following is a short summary, where $H(f)$ describes the frequency response of an LTI system and whose inverse Fourier transform $h(t)$ is the impulse response. The laws and principles are applied more frequently in the »$\text{exercises}$« for this chapter »System Description in Time Domain«.
Here, we also refer to the (German language) didactic video "Gesetzmäßigkeiten der Fouriertransformation" ⇒ "Regularities to the Fourier transform".
In the following equations the short symbol of the Fourier transformation is used. The filled-out circle indicates the spectral domain, the white one the time domain.
- »Multiplication« by a constant factor:
- $$k \cdot H(f)\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,k \cdot h(t).$$
- For $k \lt 1$ one deals with attenuation, while $k \gt 1$ stands for amplification.
- »Similarity Theorem«:
- $$H({f}/{k})\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,|k| \cdot h(k\cdot t).$$
- This implies: Compression $(k < 1)$ of the frequency response results in a wider and lower impulse response.
- Stretching $(k > 1)$ of $H(f)$ makes $h(t)$ narrower and higher.
- »Displacement Theorem« in the frequency and time domain:
- $$H(f - f_0) \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, h( t )\cdot {\rm e}^{\hspace{0.05cm}{\rm j}2\pi f_0 t},$$
- $$H(f) \cdot {\rm e}^{-{\rm j}2\pi ft_0}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, h( t- t_0 ).$$
- A shift by $t_0$ $($»transit time»$)$ thus leads to multiplication by a complex exponential function in the frequency domain.
- Thereby, the amplitude response $|H(f)|$ does not change.
- »Differentiation Theorem« in the frequency and time domain:
- $$\frac{1}{{{\rm j}2\pi }} \cdot \frac{{{\rm d}H( f )}}{{{\rm d}f}} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,- t \cdot h( t ),$$
- $${\rm j}\cdot 2\pi f \cdot H( f ){}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \frac{{{\rm d}h( t )}}{{\rm d}t}.$$
- A differentiating element in the LTI system leads to a multiplication by ${\rm j}\cdot 2πf$ in the frequency domain
- and thus among other things to a phase rotation by $90^{\circ}$.
Causal systems
$\text{Definition:}$ An LTI system is said to be $\text{causal}$ if the impulse response $h(t)$ – that is the inverse Fourier transform of the frequency response $H(f)$ – satisfies the following condition:
- $$h(t) = 0 \hspace{0.25cm}{\rm for}\hspace{0.25cm} t < 0.$$
If this condition is not met, the system is »non–causal« $($or »acausal«$)$.
$\text{Please note:}$ Any realizable system is causal.
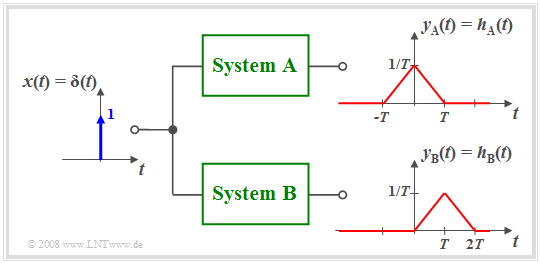
$\text{Example 2:}$ The diagram illustrates the differences between the non–causal system $\rm A$ and the causal system $\rm B$.
- In system $\rm A$ the effect starts earlier $($at $t =\hspace{0.05cm} –T)$ than the cause $($Dirac delta function at $t = 0)$, which of course is not possible in practice.
- Almost all non–causal systems can be transformed into a feasible causal system using a transit time $\tau$.
- For example, with $\tau = T$ the following holds: $h_{\rm B}(t) = h_{\rm A}(t - T).$
All statements made so far apply for causal as well as non–causal systems.
However, for the description of causal systems some specific properties can be used as explained in the third main chapter »Description of Causal Realizable Systems« of $\text{this book}$.
In this first and the following second main chapter we mainly consider non–causal systems since their mathematical description is usually simpler.
- So in this example, the frequency response $H_{\rm A}(f)$ is real,
- while for $H_{\rm B}(f)$ the additional term ${\rm e}^{–{\rm j2π}f\hspace{0.05cm}T}$ has to be considered.
Computation of the output signal
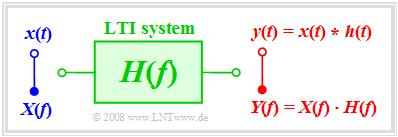
We consider the following problem: Let the input signal $x(t)$ and the frequency response $H(f)$ be known. The output signal $y(t)$ is to be determined.
If the solution is to be determined in the frequency domain, first the spectrum $X(f)$ must be determined from the given input signal $x(t)$ via $\text{Fourier transform}$ and multiplied by the frequency response $H(f)$. By the $\text{inverse Fourier transform}$ of the product the signal $y(t)$ is obtained.
Here is a summary of the entire solution process:
- $${\rm 1.\,\, step\hspace{-0.1cm} :}\hspace{0.5cm} X(f)\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, x( t )\hspace{1.55cm}{\rm input\:spectrum},$$
- $${\rm 2.\,\, step\hspace{-0.1cm}:}\hspace{0.5cm}Y(f)= X(f) \cdot H(f) \hspace{0.82cm}{\rm output\:spectrum},$$
- $${\rm 3.\,\, step\hspace{-0.1cm}:}\hspace{0.5cm} y(t)\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, Y(f )\hspace{1.55cm}{\rm output\:signal}.$$
The same result is obtained after the computation in the time domain by first determining the impulse response $h(t)$ from the frequency response $H(f)$ by means of the »inverse Forier transform« and then applying the convolution operation:
- $$y(t) = x (t) * h (t) = \int_{ - \infty }^{ + \infty } {x ( \tau )} \cdot h ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$
- The results are identical for both approaches.
- Purposefully, the procedure of solution with less computational effort should be chosen.
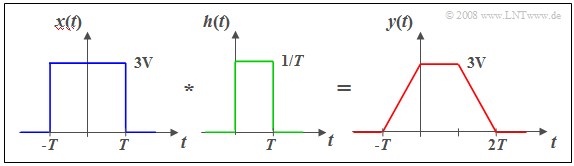
$\text{Example 3:}$ At the input of a filter with rectangular impulse response $h(t)$ of width $T$ $($see $\text{Example 1)}$ a rectangular pulse $x(t)$ of duration $2T$ is applied.
In this case, direct computation in the time domain is more convenient:
- The convolution of two rectangles $x(t)$ and $h(t)$ of different widths results in a trapezoidal output signal $y(t)$.
- The low-pass property of the filter can be seen from the finite edge steepness of $y(t)$.
- The pulse height $(3\text{ V)}$ is preserved in this example because of
- $$H(f = 0) = 1/T · T = 1.$$
Step response
$\text{Definition:}$ In practice, one of the often used input functions $x(t)$ in order to measure $H(f)$ is the »jump function«
- $${\rm \gamma}(t) = \left\{ \begin{array}{l} \hspace{0.25cm}0 \\ 0.5 \\ \hspace{0.25cm} 1 \\ \end{array} \right.\quad \quad\begin{array}{*{20}c} \text{for} \\ \text{for}\\ \text{for} \\ \end{array}\begin{array}{*{20}c}{\vert \hspace{0.05cm} t\hspace{0.05cm} \vert < 0,} \\ {\vert \hspace{0.05cm}t\hspace{0.05cm} \vert = 0,} \\ {\vert \hspace{0.05cm} t \hspace{0.05cm} \vert > 0.} \\ \end{array}$$
The »step response« $\sigma(t)$ is the response of the system if the jump function $\gamma(t)$ is applied to the input:
- $$x(t) = {\rm \gamma}(t)\hspace{0.5cm}\Rightarrow \hspace{0.5cm} y(t) = {\rm \sigma}(t).$$
The computation in the frequency domain would be a bit laborious here because the following equation would have to be applied:
- $${\rm \sigma}(t)\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, X(f ) \cdot H(f) =\left({1}/{2}\cdot \delta(f) + \frac{1}{{\rm j}\cdot 2\pi f} \right) \cdot H(f).$$
In contrast to this, the computation in the time domain leads directly to the result:
- $${\rm \sigma}(t) = \int_{ - \infty }^{ t } {h ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$
For causal sytems $h(\tau) = 0$ holds for $\tau \lt 0$, such that the lower limit of integration in the above equation can be set to $\tau = 0$.
$\text{Proof:}$ The above result is also insightful for the following reason:
- The jump function $\gamma(t)$ is related to the Dirac delta function $\delta(t)$ as follows:
- $${\rm \gamma}(t) = \int_{ - \infty }^{ t } {\delta ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$
- Since we have assumed linearity and integration is a linear operation the corresponding relationship also applies to the output signal:
- $${\rm \sigma}(t) = \int_{ - \infty }^{ t } {h ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$
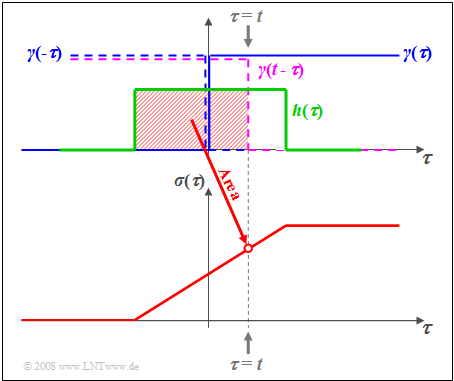
$\text{Example 4:}$ The graph illustrates the facts for the rectangular impulse response $h(\tau)$.
$\text{Note:}$
- The abscissa has been renamed to $\tau$.
- The jump function $\gamma(\tau)$ is drawn in blue.
- $\gamma(t - \tau)$ is obtained by mirroring and shifting ⇒ curve dashed in violet.
- The red shaded area thus gives the step response $\sigma(\tau)$ at time $\tau = t$ .
Exercises for the chapter
Exercise 1.3: Measured Step Response
Exercise 1.3Z: Exponentially Decreasing Impulse Response
Exercise 1.4: Low-Pass Filter of 2nd Order
Exercise 1.4Z: Everything Rectangular