Some Low-Pass Functions in Systems Theory

1 General remarks
2 Ideal low-pass filter – Rectangular-in-frequency
3 Slit low-pass filter – Rectangular-in-time
4 Gaussian low-pass filter
5 Trapezoidal low-pass filter
6 Raised-cosine low-pass filter
7 Cosine–square low-pass filter
8 Derivation of system theoretical high-pass functions
9 Exercises for the chapter

General remarks

All low-pass functions described in the next sections have the following properties:

The frequency response $H(f)$ is real and even so that according to the $\text{Assignment Theorem}$ the associated impulse response $h(t)$ is always real and even, too.

Thus, it is obvious that the systems considered here are non-causal and hence not realizable. The description of causal systems is given in the chapter »Description of Causal Realizable Systems« of this book.

The advantage of these »system theoretical filter functions« is the simple description by at most two parameters such that the filter influence can be represented in a transparent way.

The most important frequency response parameter is the »equivalent bandwidth« according to the definition via the equal-area rectangle:

$$\Delta f = \frac{1}{H(f=0)}\cdot \int_{-\infty}^{+\infty}H(f) \hspace{0.15cm} {\rm d}f.$$

According to the so-called »Reciprocity Theorem of time duration and bandwidth« the »equivalent duration of the impulse response« is thus fixed, which is also defined via the equal-area rectangle:

$$\Delta t = \frac{1}{h(t=0)}\cdot \int_{-\infty}^{+\infty}h(t) \hspace{0.15cm} {\rm d}t = \frac{1}{\Delta f}.$$

The direct signal $\rm (DC)$ transmission factor is always assumed to be $H(f = 0) = 1$ unless explicitly stated otherwise.

From every low-pass function corresponding high-pass functions can be derived as shown in the section »Derivation of system theoretical high-pass functions«.

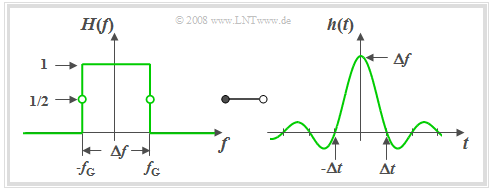
Ideal low-pass filter – Rectangular-in-frequency

$\text{Definition:}$ An »ideal low-pass filter« is on hand if its frequency response has the following rectangular shape:

$$H(f) = H_{\rm RLP}(f) =\left\{ \begin{array}{l} \hspace{0.25cm}1 \\ 0.5 \\\hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad\begin{array}{*{10}c} \text {for} \\ \text {for} \\ \text {for} \\ \end{array}\begin{array}{*{20}c}{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert< \Delta f/2,} \\{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert = \Delta f/2,} \\{\vert \hspace{0.005cm}f\hspace{0.05cm} \vert > \Delta f/2.} \\\end{array}$$

We sometimes also use the term »rectangular low-pass filter« $\rm (RLP)$.
Here $Δf$ denotes the »system theoretical bandwidth«.
$f_{\rm G}=Δf/2$ denotes the »cut-off frequency« $($German: "Grenzfrequenz" ⇒ subscript $\rm G)$.

Ideal low-pass filter: Frequency response and impulse response

The graph shows such an ideal low-pass filter in the frequency and time domain.

The following can be concluded from these curves:

Due to the abrupt, infinitely steep roll-off the »3 dB cut-off frequency« ⇒
$f_{\rm G}$ is here exactly half the »system theoretic bandwidth« $Δf$.

All spectral components with $f \lt f_{\rm G}$ are transmitted undistorted ⇒ »pass band«.

All components with $f \gt f_{\rm G}$ are completely suppressed ⇒ »stop band«.

By definition, $H(f) = 0.5$ holds for $f = \pm f_{\rm G}$.

Description of the ideal low-pass filter in the time domain:

According to the inverse Fourier transform the »impulse response« $($right diagram$)$:

$$h(t) = h_{\rm RLP}(t) =\Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t)\hspace{0.55cm}{\rm{with}}\hspace{0.7cm}{\rm si}(x) ={\sin(x)}/{x},\hspace{0.5cm}{\rm or}$$

$$h_{\rm RLP}(t) =\Delta f \cdot {\rm sinc}(\Delta f \cdot t)\hspace{0.7cm}{\rm{with}}\hspace{0.7cm}{\rm sinc}(x) ={\sin(\pi x)}/{(\pi x)}.$$

$h(t)$ extended to infinity on both sides and exhibits equidistant zero-crossings at an interval of $Δt = 1/ Δf$.

The asymptotic decay is inversely proportional to time $|t|$:

$$|h(t)| = \frac{\Delta f}{\pi \cdot \Delta f \cdot |t|} \cdot \left |{\rm sin}(\pi \cdot \Delta f\cdot t )\right | \le \frac{1}{\pi \cdot |t|}.$$

It follows that the impulse response is certainly less than $1‰$ of the impulse maximum only for times $t \gt t_{1‰} = 318 \cdot \Delta t$.

The step response $\sigma(t)$ is obtained from the impulse response by integration and is:

$${\sigma}(t) = \int_{ - \infty }^{ t } {h ( \tau )} \hspace{0.1cm}{\rm d}\tau = \frac{1}{2} + \frac{1}{\pi} \cdot {\rm Si}(\pi \cdot\Delta f \cdot t ).$$

Here, the so-called »integral sine function« is used:

$${\rm Si}(x) = \int_{ 0 }^{ x } {{\rm si} ( \xi )} \hspace{0.1cm}{\rm d}\xi = x - \frac{x^3}{3 \cdot 3!} + \frac{x^5}{5 \cdot 5!} - \frac{x^7}{7 \cdot 7!}+\text{ ...}$$

$$\Rightarrow \ {\rm Si}(0) = 0, \hspace{0.3cm}{\rm Si}(\infty) = \frac{\pi}{2}, \hspace{0.3cm}{\rm Si}(-x) = -{\rm Si}(x).$$

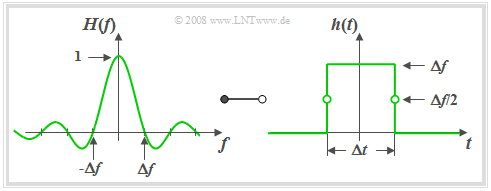
Slit low-pass filter – Rectangular-in-time

$\text{Definition:}$ An LTI system is called a »slit low-pass filter« $\rm (SLP)$ if the frequency response has the following form:

$$H(f) = H_{\rm SLP}(f)= {\rm si}(\pi {f}/{ \Delta f})\hspace{0.7cm}{\rm{where} }\hspace{0.7cm}{\rm si}(x) ={\sin(x)}/{x},\hspace{0.7cm}{\rm or}$$

$$\hspace{2.1cm}H_{\rm SLP}(f)= {\rm sinc}({f}/{ \Delta f})\hspace{0.7cm}{\rm{where} }\hspace{0.7cm}{\rm sinc}(x) ={\sin(\pi x)}/{(\pi x)}.$$

Slit low-pass filter: Frequecy response and respective impulse response

From the graph on the left it can be seen that the frequency response $H_{\rm SLP}(f)$ of the slit low-pass filter is identical in shape to the impulse response $h_{\rm RLP}(t)$ of the rectangular low-pass filter.
According to the »Duality Theorem« ⇒ the impulse response $h_{\rm SLP}(t)$ of the slit low-pass filter must also have the same form as the frequency response $H_{\rm RLP}(f)$ of the ideal low-pass filter ⇒ "rectangular-in-time".
Thus, with the »equivalent duration of the impulse response« $Δt = 1/ Δf$ the following holds:

$$h(t) = h_{\rm SLP}(t) = \left\{ \begin{array}{l} \hspace{0.25cm}\Delta f \\ \Delta f/2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} \text{for} \\ \text{for} \\ \text{for} \\ \end{array}\begin{array}{*{20}c} {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert < \Delta t/2,} \\ {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert = \Delta t/2,} \\ {\vert \hspace{0.005cm}t\hspace{0.05cm} \vert > \Delta t/2.} \\ \end{array}$$

Based on the graph on the right the following statements can be derived:

The slit low-pass filter in this form is also non-causal. However, adding a transit time of $Δt/2$ or more renders the system causal and thus realizable.

The slit low-pass filter acts as an integrator over the time period $Δt$:

$$y(t) = x (t) * h (t) = \frac{1}{\Delta t} \cdot \int\limits_{ t - \Delta t/2 }^{ t + \Delta t/2 } {x ( \tau )} \hspace{0.1cm}{\rm d}\tau.$$

If $x(t)$ is a harmonic oscillation with frequency $f_0 = k \cdot Δf$ $($where $k$ is an integer$)$, then it integrates exactly over $k$ periods and $y(t) = 0$ holds.

This is also shown by the zeros of $H(f)$.

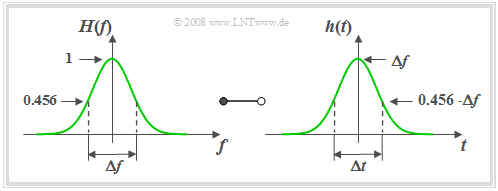
Gaussian low-pass filter

A filter function frequently used for system-theoretical investigations is the Gaussian low-pass filter, which can also be described by only one parameter, namely the »equivalent bandwidth» $Δf$.

$\text{Definition:}$ For the frequency response and the impulse response of the »Gaussian low-pass filter« $\rm (GLP)$ the following holds:

$$H(f) = H_{\rm GLP}(f)= {\rm e}^{-\pi(f/\Delta f)^2}\hspace{0.15cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.15cm}h(t) = h_{\rm GLP}(t) = \Delta f \cdot {\rm e}^{-\pi(\Delta f \cdot \hspace{0.03cm} t)^2} .$$

The name goes back to the mathematician, physicist and astronomer $\text{Carl-Friedrich Gauß}$. Gauß did not deal with this subject matter himself, but the mathematical form of the frequency response and impulse response bear a resemblance to the so-called »Gaussian formula« which he discovered for probability theory.

Gaussian low-pass filter: Frequency response and impulse response

Based on this graph the following statements can be made:

The »equivalent pulse duration« $Δt$ is also defined via the area-equal rectangle and is equal to the reciprocal of the »equivalent bandwith« $Δf$.
A narrow-band $($small $Δf)$ filter function $H(f)$ results in a wide $($large $Δt)$ and simultaneously low impulse response $h(t)$.
The so-called »Reciprocity Theorem« of time duration and bandwidth can be shown particularly clearly in the example of the Gaussian low-pass filter.
The frequency and time domain representations are in principle of the same form. The Gaussian function is also said to be invariant to Fourier transform.
The Gaussian low-pass filter is – like the ideal low-pass filter – strongly non-causal and $($exactly$)$ realizable only with infinitely large transit time due to the infinite propagation of its impulse response.
However, it must be taken into account that $h(t)$ has already decayed to $1‰$ of its maximum value at $t = 1.5 \cdot Δt$. For $t = 3 \cdot Δt$ we even get $h(t) ≈ 5 · 10^{–13} · h(0)$.
These numerical values show that the Gaussian low-pass filter can be used feasibly for practical simulations as long as runtimes do not play a system-limiting role.
The »step response« $σ(t)$ is given for the »Gaussian error function« $ϕ(x)$, which is usually given in tabular form in formula collections:

$$\sigma(t) = \int_{ -\infty }^{ t } {h(\tau)} \hspace{0.1cm}{\rm d}\tau = {\rm \phi}\left( \sqrt{2 \pi }\cdot{t}/{\Delta t} \right) \hspace{0.7cm}{\rm{where}}\hspace{0.7cm}{\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot \int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$$

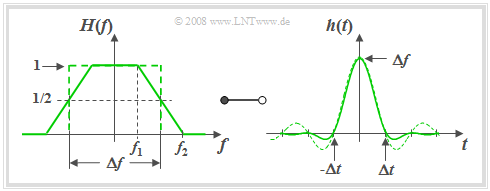
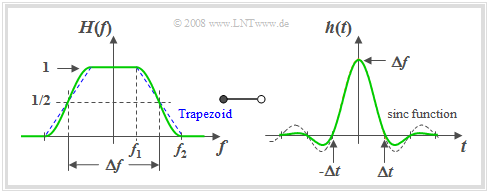
Trapezoidal low-pass filter

The low-pass functions described so far depend on only one parameter – the »equivalent bandwidth« $Δf$. Here, the edge steepness for a given filter type was fixed. Now a low-pass filter with parameterisable edge steepness is described.

$\text{Definition:}$ The frequency response of the »trapezoidal low-pass filter« $\rm (TLP)$ with cut-off frequencies $f_1$ and $f_2 \ge f_1$:

$$H(f) = H_{\rm TLP}(f)= \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \frac{f_2 - \vert f \vert }{f_2 -f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} \text{for} \\ \text{for} \\ \text{for} \\ \end{array}\begin{array}{*{20}c} {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert < f_1,} \\ {f_1 \le \vert \hspace{0.005cm} f\hspace{0.05cm} \vert \le f_2,} \\ {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert > f_2.} \\ \end{array}$$

Instead of $f_1$ and $f_2$ the following parameters can be used to describe $H(f)$:

the »equivalent bandwidth« determined via the equal-area rectangle:

$$\Delta f = f_1 + f_2.$$

the »roll-off factor« $($in frequency domain$)$ as a measure for the edge steepness:

$$r_{\hspace{-0.05cm}f} = \frac{f_2 - f_1}{f_2 + f_1}.$$

Special cases included in the general representation are:

the ideal rectangular low-pass filter $(r_{\hspace{-0.05cm}f} = 0)$,

the triangular low-pass filter $(r_{\hspace{-0.05cm}f} = 1)$.

For a roll-off factor of $r_f = 0.5 \ \Rightarrow \ f_2 = 3f_1$ the following graph shows the frequency response $H(f)= H_{\rm TLP}(f)$ on the left and on the right the impulse response

$$h(t) = h_{\rm TLP}(t) =\Delta f \cdot {\rm sinc}(\Delta f \cdot t )\cdot {\rm sinc}(r_{\hspace{-0.05cm}f} \cdot \Delta f \cdot t )\hspace{0.7cm}{\rm{where}}\hspace{0.7cm}{\rm sinc}(x)= \frac{\sin(\pi x)}{\pi x}.$$

The time-dependent $\rm sinc$–curve of the rectangular low-pass filter with the same equivalent bandwidth is shown dashed for comparison. With the help of the graph and the above equations the following statements can be made:

Trapezoidal low-pass filter: Frequency response and impulse response

The trapezoidal shape is obtained, for example, by convolution of two rectangles of widths $Δf$ and $r_f \cdot Δf$.
According to the convolution theorem the impulse response is thus the product of two $\rm sinc$–functions with arguments $Δf · t$ and $r_{\hspace{-0.05cm}f} · Δf · t$.
The first $\rm sinc$–function is part of the $h(t)$ equation for all values of $r_{\hspace{-0.05cm}f}$ and always results in equivalent zero-crossings in the distance $1/Δf$.
For $0 \lt r_{\hspace{-0.05cm}f} \lt 1$ there are further zero-crossings at multiples of $Δt/r_{\hspace{-0.05cm}f}$.
The larger $r_{\hspace{-0.05cm}f}$ is $($i.e. for a given $Δf$ with a flatter edge$)$, the faster is the asymptotic decay of the impulse response $h(t)$.
The fastest possible decay is obtained for the triangular low-pass filter ⇒ $r_{\hspace{-0.05cm}f} = 1$, $f_1 = 0$, $f_2 = Δf$. For this, the following holds in frequency and time domains:

$$H(f) = \left\{ \begin{array}{c} \hspace{0.25cm} \frac{{\rm \Delta}f -|f|}{{\rm \Delta}f} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\hspace{1cm} \left| \hspace{0.005cm}f\hspace{0.05cm} \right| \le {\rm \Delta}f ,} \\ {\hspace{1cm}\left|\hspace{0.005cm} f \hspace{0.05cm} \right| \ge {\rm \Delta}f } \\ \end{array},$$

$$h(t) = \Delta f \cdot {\rm sinc}^2( \Delta f \cdot t ),\hspace{0.2cm}{\rm{where}}\hspace{0.4cm}{\rm sinc}(x)= \frac{\sin(\pi x)}{\pi x}.$$

Raised-cosine low-pass filter

Like the »trapezoidal low-pass filter« this low-pass filter is also described by two parameters, which are

the equivalent bandwidth $Δf$,

the roll-off factor $r_{\hspace{-0.05cm}f}$.

Its value range lies between $r_{\hspace{-0.05cm}f} = 0$ $($rectangular low-pass filter$)$ and $r_{\hspace{-0.05cm}f} = 1$ $($cosine–squared low-pass filter$)$.

$\text{Definition:}$ With cut-off frequencies $f_1 = Δf · (1 – r_{\hspace{-0.05cm}f})$ and $f_2 = Δf · (1 + r_{\hspace{-0.05cm}f})$ the frequency response of the »raised-cosine low-pass filter« $\rm (RCLP)$:

$$H(f) = H_{\rm RCLP}(f) =\left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \cos \left( \frac{ \vert f \vert - f_1}{f_2 -f_1}\cdot \pi/2\right) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} \text{for} \\ \text{for} \\ \text{for} \\ \end{array}\begin{array}{*{20}c} {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert < f_1,} \\ {f_1 \le \vert \hspace{0.005cm} f\hspace{0.05cm} \vert \le f_2,} \\ {\hspace{0.94cm}\vert \hspace{0.005cm} f\hspace{0.05cm} \vert> f_2.} \\ \end{array}$$

Raised-cosine low-pass filter and respective impulse response

The graph shows $H(f)$ on the left and on the right the impulse response

$$h(t) = h_{\rm RCLP}(t) =\Delta f \hspace{-0.05cm}\cdot\hspace{-0.05cm} {\rm sinc}( \Delta f \hspace{-0.05cm}\cdot\hspace{-0.05cm} t )\hspace{-0.05cm}\cdot\hspace{-0.05cm} \frac {\cos(\pi \cdot r_{\hspace{-0.05cm}f} \cdot \Delta f \cdot t )}{1 - (2 \cdot r_f \cdot \Delta f \cdot t)^2}.$$

For these graphs the roll-off factor $r_{\hspace{-0.05cm}f} = 0.5$ was used. In other words: $f_2 = 3 \cdot f_1.$

The following is drawn in dashed lines for comparison:

in the frequency domain the trapezoidal low-pass filter and

in the time domain the $\rm sinc$ function.

$\text{Please note:}$

The $\rm sinc$–function is not the inverse Fourier transform of the trapezoidal low-pass filter drawn in blue on the left. It rather describes the ideal rectangular low-pass filter in the time domain, which is not shown in the left graph.

Based on this graph and the above equations the following statements can be made:

The impulse response $h(t)$ of the raised-cosine low-pass filter has zeros at all multiples of $Δt = 1/Δf$, which are due to the $\rm sinc$–function shown in dashed lines in the right-hand figure.
The last term in the $h(t)$ equation results in further zeros at multiples of $Δt/r_f$. If $1/r_f$ is an integer as in the above graph $(1/r_f = 2)$, these new zeros coincide with the other zeros and thus are not discernible.
The larger the roll-off factor $r_f$ and thus the flatter the roll-off is, the more favourable is the transient behaviour of the raised-cosine low-pass filter.
The raised-cosine low-pass filter usually exhibits a better asymptotic transient behaviour than the trapezoidal low-pass filter with same $r_f$ although the latter has a flatter edge at least at frequency $Δf/2$.
This suggests that the transient behaviour is not only affected by points of discontinuity $($as in the case of the rectangle$)$ but also by kink points as in the case of the trapezoidal low-pass filter.

Cosine–square low-pass filter

$\text{Definition:}$ For $f_1 = 0$, $f_2 = Δf$ ⇒ $r_f = 1$ the »cosine–square low-pass filter« $\rm (CSLP)$ is obtained as a special case. Its impulse response can also be represented as follows:

$$H(f) = H_{\rm CSLP}(f)= \cos^2\Big(\frac{\vert f \vert \hspace{0.05cm}\cdot\hspace{0.05cm} \pi}{2\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta f}\Big). $$

Outside this inner frequency range, $H_{\rm CSLP}(f)=0$.

For the impulse response one obtains according to the inverse Fourier transform after some transformations:

$$h(t)=h_{\rm CSLP}(t)= \Delta f \cdot {\rm sinc}(\Delta f \cdot t)\cdot \big [{\rm sinc}(\Delta f\cdot t +0.5)+{\rm sinc}(\Delta f\cdot t -0.5)\big ],$$

$$T=1/\Delta f \hspace{0.5cm}\Rightarrow \hspace{0.5cm} h(t)=1/T \cdot {\rm sinc}(t/T)\cdot \big [{\rm sinc}(t/T +0.5)+{\rm sinc}(t/T -0.5)\big ].$$

Because of the first ${\rm sinc}$–function, $h(t)=0$ for multiples of $T=1/\Delta f$ ⇒ the equidistant zero-crossings of the cosine–rolloff lowpass are preserved.
Because of the bracket expression, $h(t)$ now exhibits further zero-crossings at $t=\pm1.5 T$, $\pm2.5 T$, $\pm3.5 T$, ... but not at $t=\pm0.5 T$.
For $t=\pm0.5 T$ the impulse response has the value $\Delta f/2$.
The asymptotic decay of $h(t)$ in this special case runs with $1/t^3$.

$\text{Furthermore, it should be mentioned}$ that the »cosine-square low-pass filter« is the only low-pass filter that fulfils both »Nyquist criteria«. Here the »eye« in digital transmission is maximally open both vertically and horizontally ⇒ see »Definition and statements of the eye diagram«.

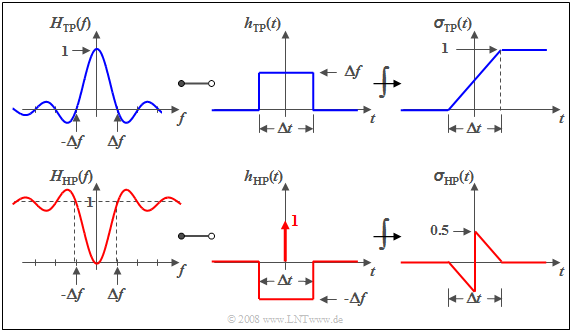
Derivation of system theoretical high-pass functions

So far, six commonly used system theoretic low-pass functions have been considered. For each individual low-pass function there is also an equivalent high-pass function.

$\text{Definition:}$ If $H_{\rm TP}(f)$ is a system–theoretical low-pass function $($German "Tiefpass" ⇒ $\text{TP)}$ with $H_{\rm TP}(f = 0) = 1$, then the »equivalent high-pass function«:

$$H_{\rm HP}(f) = 1 - H_{\rm TP}(f).$$

Thus, the descriptive quantities in the time domain are:

$$h_{\rm HP}(t) = \delta (t) - h_{\rm TP}(t),$$

$$\sigma_{\rm HP}(t) = \gamma (t) - \sigma_{\rm TP}(t). $$

Here, the following denotations are used:

$h_{\rm HP}(t)$ and $h_{\rm TP}(t)$ denote the impulse responses of the high- and low-pass filter,
$σ_{\rm HP}(t)$ and $σ_{\rm TP}(t)$ denote the respective step responses,
$γ(t)$ denotes the jump function as a result of integration over the Dirac delta function $δ(t)$.

$\text{Example 1:}$ We consider the »slit low-pass filter« ⇒ »rectangular-in-time» which is characterized by

Construction of high-pass functions $H_{\rm HP}(f)$, $h_{\rm HP}(t)$, $\sigma_{\rm HP}(t)$ from the
corresponding low-pass functions $H_{\rm TP}(f)$, $h_{\rm TP}(t)$, $\sigma_{\rm TP}(t)$