Difference between revisions of "Modulation Methods/Influence of Noise on Systems with Angle Modulation"
| (42 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Angle Modulation and Demodulation |
| − | |Vorherige Seite= | + | |Vorherige Seite=Frequency Modulation (FM) |
| − | |Nächste Seite= | + | |Nächste Seite=Pulse Code Modulation |
}} | }} | ||
| − | == | + | ==Signal-to-noise power ratio in PM== |
| − | + | <br> | |
| + | To investigate noise behavior, we will take the [[Modulation_Methods/Quality_Criteria#Some_remarks_on_the_AWGN_channel_model|$\text{AWGN channel}$]] as our starting point and calculate the sink SNR $ρ_v$ as a function of | ||
| + | [[File:EN_Mod_T_3_3_S1.png|right|frame|Signal-to-noise power ratio in phase modulation]] | ||
| + | *the frequency ("bandwidth") $B_{\rm NF}$ of the cosine source signal, | ||
| + | |||
| + | *the transmit power $P_{\rm S}$, | ||
| + | |||
| + | *the channel transmission factor $α_{\rm K}$, and | ||
| + | |||
| + | *the (one-sided) noise power density $N_0$. | ||
| − | + | The principle procedure is described in detail in the section [[Modulation_Methods/Quality_Criteria#Investigations_at_the_AWGN_channel|"Investigations at the AWGN channel"]]: | |
| − | |||
| − | |||
| − | |||
| + | If the performance parameter | ||
| + | :$$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$ | ||
| + | is sufficiently large, the following approximation is obtained for phase modulation $\rm (PM)$ with modulation index $η$ : | ||
| + | :$$\rho_{v } \approx {\eta^2}/{2} \cdot\xi \hspace{0.05cm}.$$ | ||
| − | + | This means that for phase modulation, the sink SNR increases quadratically with increasing $η$. | |
| + | The exact calculation of $ρ_v$ is not very simple, and is also laborious. Here, we will only briefly describe the calculation steps: | ||
| + | #Approximate the white noise $n(t)$ for the high-frequency bandwidth $B_{\rm HF}$ by a sum of sinusoidal disturbance sources (German: "Störquellen" ⇒ subscript: "St") spaced by $f_{\rm St}$ (see second sketch in the following section). | ||
| + | #Calculate the S/N ratio after demodulation for each sinusoidal disturbance source and sums the individual contributions, which are now all in the low-frequency (German: "Niederfrequenz" ⇒ subscript: "NF") region $|f| < B_{\rm NF}$. | ||
| + | #The above simple result is obtained after the boundary transition $f_{\rm St} → 0$. The sum then turns into an integral and this can be solved approximately. | ||
| − | [[File: | + | ==Signal-to-noise power ratio in FM== |
| + | <br> | ||
| + | For calculation one uses the fact that the FM demodulator can be realized with a PM demodulator and a differentiator. | ||
| + | [[File:EN_Mod_T_3_3_S2a.png|right|frame|FM demodulator: PM demodulator and differentiator]] | ||
| + | *The block diagram on the right refers only to the noise signals ⇒ $s(t) = 0$. | ||
| + | |||
| + | *Thus the received signal $r(t) = n(t)$, where we assume for $n(t)$ additive Gaussian white noise with center frequency $f_{\rm T}$ and high-frequency bandwidth $B_{\rm HF}$. | ||
| − | |||
| − | |||
| − | + | When calculating the noise power density after the FM demodulator, consider: | |
| + | *The noise power density ${\it Φ}_{v,\hspace{0.1cm}{\rm PM}}(f)$ after the PM demodulator is in the low-pass range, has the (one-sided) bandwidth $B_{\rm NF}$ and is "white" (see left plot in the graph below). | ||
| − | + | *The power density at the output of a linear system with frequency response $H(f)$ is generally when the noise power density ${\it Φ}_{v,\hspace{0.1cm}{\rm PM}}(f)$ is applied to the input: | |
| − | * | + | :$${ \it \Phi}_{v {\rm , \hspace{0.1cm}FM} } (f) = { \it \Phi}_{v {\rm , \hspace{0.1cm}PM} } (f) \cdot |
| − | + | |H(f)|^2 \hspace{0.05cm}.$$ | |
| − | |||
| − | + | *The differentiator is just such a linear system. Its frequency response $H(f)$ increases linearly with $f$, and it is applied to the noise power density at the output of the FM demodulator (see the right plot in the lower graph): | |
| − | + | :$${ \it \Phi}_{v {\rm , \hspace{0.1cm}FM} } (f) = {\rm const. } \cdot | |
| + | f^2 \cdot { \it \Phi}_{v {\rm , \hspace{0.1cm}PM} }(f) \hspace{0.05cm}.$$ | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\rm Conclusion\text{:}$ | ||
| + | Taking this result into account, one arrives after a longer calculation at the following »'''sink SNR'''« (if the performance parameter $ξ$ is sufficiently large): | ||
| + | [[File:P_ID1114__Mod_T_3_3_S2b_neu.png |right|frame| Noise power density spectra for PM (left) and FM (right)]] | ||
| + | :$$\rho_{v } \approx \frac{3\cdot \eta^2}{2} \cdot \frac{\alpha_{\rm K}^2 \cdot P_{\rm S} }{N_0 \cdot B_{\rm NF} } = 3/2 \cdot{\eta^2} \cdot\xi \hspace{0.05cm}.$$ | ||
| − | + | The graph illustrates: | |
| − | + | * The noise power density ${\it Φ}_{v,\hspace{0.1cm}{\rm FM} }(f)$ is not white, unlike ${\it Φ}_{v,\hspace{0.1cm}{\rm PM} }(f)$. | |
| − | + | ||
| − | + | *Rather, ${\it Φ}_{v,\hspace{0.1cm}{\rm FM} }(f)$ increases with $f^2$ towards the limits $(\pm B_{\rm NF} )$. | |
| − | * | + | |
| − | + | *When $f = 0$, ${\it Φ}_{v,\hspace{0.1cm}{\rm FM} }(f)$ has no noise components.}} | |
| − | |||
| − | |||
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[File: | + | ==System comparison of AM, PM and FM with respect to noise== |
| + | <br> | ||
| + | As explained in detail in the [[Modulation_Methods/Quality_Criteria#Investigations_at_the_AWGN_channel|"Investigations at the AWGN channel"]] section and applied to amplitude modulation in the [[Modulation_Methods/Synchronous_Demodulation#Sink_SNR_and_the_performance_parameter|"Sink SNR and the performance parameter"]] section, we again consider the double-logarithmic plot of the sink SNR $ρ_v$ versus the performance parameter | ||
| + | [[File:EN_Mod_T_3_3_S3_neu.png|right|frame|System comparison of AM, PM and FM concerning noise.<br>Note: All curves are quantitatively valid only for harmonic oscillations (i.e. for only a single frequency). However, for a mix of frequencies – which is always present in practice – the curves apply at least qualitatively.]] | ||
| − | + | :$$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}.$$ | |
| − | |||
| + | These curves, which are to be understood qualitatively, are to be interpreted as follows: | ||
| − | + | *The comparison curve shows »'''DSB–AM without a carrier'''« ⇒ modulation depth $m → ∞$. Here, $ρ_v = ξ$, and double-logarithmic representation also yields a $45^\circ$ straight line through the origin. | |
| + | *The »'''FM curve'''« with $η = 3$ lies around $10 · \lg \ 13.5 ≈ 11.3 \ \rm dB$ above the AM curve. Visibly, the superior noise performance of frequency modulation can be explained by the fact that an additive noise component affects the position of the zero crossings less than it changes the amplitude values. | ||
| − | + | *When noise is strong and thus the performance parameter very small $(10 · \lg \ ξ ≤ 15 \ \rm dB)$, any kind of angle modulation $\rm (WM)$ is not recommended. Due to noise, zero crossings can then disappear completely and making their detection impossible. This is referred to as "WM threshold effect". | |
| + | *With regard to noise, the greatest possible modulation index should be aimed for with any type of angle modulation. Like this, the FM curve for $η = 10$ is about $10.4 \ \rm dB$ above the curve for $η = 3$. | ||
| − | * | + | *However, it must be taken into account that a larger $η$ also requires a larger bandwidth or – for given channel bandwidth – causes stronger non-linear distortions. |
| − | |||
| − | * | + | *For the same modulation index, phase modulation $\rm (PM)$ is always $10 \cdot \lg \ 3 ≈ 4.8 \ \rm dB$ worse than frequency modulation $\rm (FM)$. This is one of the reasons why analog phase modulation is in practice of little importance. In contrast, the "Phase Shift Keying" $\rm (PSK)$ variant is used more frequently than "Frequency Shift Keying" $\rm (FSK)$ in digital modulation because of other advantages. |
| + | ==Pre-emphasis and de-emphasis== | ||
| + | <br> | ||
| + | An important result of the last sections was that the sink SNR in frequency modulation $\rm (FM)$ corresponding to $\rho_{v } \approx 1.5 \cdot{\eta^2} \cdot\xi \hspace{0.05cm}$ depends quadratically on the modulation index by close approximation. | ||
| + | *However, since in frequency modulation the modulation index $η$ is inversely proportional to the frequency $f_{\rm N}$ of the source signal, | ||
| + | |||
| + | *the sink SNR also depends on $f_{\rm N}$. | ||
| − | |||
| + | This leads to the following consequences: | ||
| − | * | + | *If the source signal consists of several frequencies, the higher frequencies have a smaller modulation index $η$ after FM modulation than lower frequencies. |
| + | *This also means: The higher frequency components $($with smaller $η)$ are therefore noisier than lower frequencies, unless special measures are taken. | ||
| − | + | [[File:EN_Mod_T_3_3_S4_neu.png|right|frame|Magnitude frequency responses for <br>pre-emphasis $\rm (PE)$ and de-emphasis $\rm (DE)$]] | |
| − | + | One such measure is a »'''pre-emphasis'''«. | |
| + | #Here, higher frequencies are boosted by a high-pass filter network $H_{\rm PE}(f)$ which increases only their modulation index $η$. | ||
| + | #The transmit-side "pre-emphasis" must be reversed at the receiver by a $H_{\rm DE}(f) = 1/H_{\rm PE}(f)$ network. This lowering of the higher frequencies is called »'''de-emphasis'''«. | ||
| + | The diagram shows a possible example of the filter functions for | ||
| + | *pre-emphasis (blue) ⇒ $|H_{{\rm PE} } (f)| = \sqrt{1 + \left({f}/{f_{\rm G}}\right)^2}\hspace{0.05cm},$ | ||
| + | *de-emphasis (red) ⇒ $|H_{{\rm DE} } (f)| = |H_{{\rm PE} } (f)|^{-1} \hspace{0.05cm}.$ | ||
| + | ==Exercises for the chapter== | ||
| + | <br> | ||
| + | [[Aufgaben:Exercise_3.10:_Noise_Power_Calculation|Exercise 3.10: Noise Power Calculation]] | ||
| + | [[Aufgaben:Exercise_3.10Z:_Amplitude_and_Angle_Modulation_in_Comparison|Exercise 3.10Z: Amplitude and Angle Modulation in Comparison]] | ||
| + | [[Aufgaben:Exercise_3.11:_Pre-Emphase_and_De-Emphase|Exercise 3.11: Pre-Emphasis and De-Emphasis]] | ||
{{Display}} | {{Display}} | ||
Latest revision as of 15:29, 13 January 2023
Contents
Signal-to-noise power ratio in PM
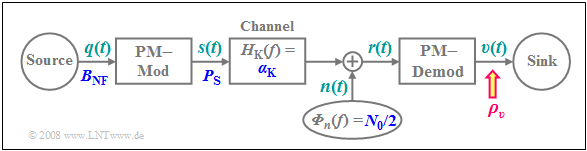
To investigate noise behavior, we will take the $\text{AWGN channel}$ as our starting point and calculate the sink SNR $ρ_v$ as a function of
- the frequency ("bandwidth") $B_{\rm NF}$ of the cosine source signal,
- the transmit power $P_{\rm S}$,
- the channel transmission factor $α_{\rm K}$, and
- the (one-sided) noise power density $N_0$.
The principle procedure is described in detail in the section "Investigations at the AWGN channel":
If the performance parameter
- $$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$
is sufficiently large, the following approximation is obtained for phase modulation $\rm (PM)$ with modulation index $η$ :
- $$\rho_{v } \approx {\eta^2}/{2} \cdot\xi \hspace{0.05cm}.$$
This means that for phase modulation, the sink SNR increases quadratically with increasing $η$.
The exact calculation of $ρ_v$ is not very simple, and is also laborious. Here, we will only briefly describe the calculation steps:
- Approximate the white noise $n(t)$ for the high-frequency bandwidth $B_{\rm HF}$ by a sum of sinusoidal disturbance sources (German: "Störquellen" ⇒ subscript: "St") spaced by $f_{\rm St}$ (see second sketch in the following section).
- Calculate the S/N ratio after demodulation for each sinusoidal disturbance source and sums the individual contributions, which are now all in the low-frequency (German: "Niederfrequenz" ⇒ subscript: "NF") region $|f| < B_{\rm NF}$.
- The above simple result is obtained after the boundary transition $f_{\rm St} → 0$. The sum then turns into an integral and this can be solved approximately.
Signal-to-noise power ratio in FM
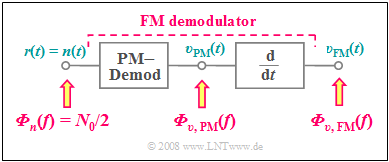
For calculation one uses the fact that the FM demodulator can be realized with a PM demodulator and a differentiator.
- The block diagram on the right refers only to the noise signals ⇒ $s(t) = 0$.
- Thus the received signal $r(t) = n(t)$, where we assume for $n(t)$ additive Gaussian white noise with center frequency $f_{\rm T}$ and high-frequency bandwidth $B_{\rm HF}$.
When calculating the noise power density after the FM demodulator, consider:
- The noise power density ${\it Φ}_{v,\hspace{0.1cm}{\rm PM}}(f)$ after the PM demodulator is in the low-pass range, has the (one-sided) bandwidth $B_{\rm NF}$ and is "white" (see left plot in the graph below).
- The power density at the output of a linear system with frequency response $H(f)$ is generally when the noise power density ${\it Φ}_{v,\hspace{0.1cm}{\rm PM}}(f)$ is applied to the input:
- $${ \it \Phi}_{v {\rm , \hspace{0.1cm}FM} } (f) = { \it \Phi}_{v {\rm , \hspace{0.1cm}PM} } (f) \cdot |H(f)|^2 \hspace{0.05cm}.$$
- The differentiator is just such a linear system. Its frequency response $H(f)$ increases linearly with $f$, and it is applied to the noise power density at the output of the FM demodulator (see the right plot in the lower graph):
- $${ \it \Phi}_{v {\rm , \hspace{0.1cm}FM} } (f) = {\rm const. } \cdot f^2 \cdot { \it \Phi}_{v {\rm , \hspace{0.1cm}PM} }(f) \hspace{0.05cm}.$$
$\rm Conclusion\text{:}$ Taking this result into account, one arrives after a longer calculation at the following »sink SNR« (if the performance parameter $ξ$ is sufficiently large):
- $$\rho_{v } \approx \frac{3\cdot \eta^2}{2} \cdot \frac{\alpha_{\rm K}^2 \cdot P_{\rm S} }{N_0 \cdot B_{\rm NF} } = 3/2 \cdot{\eta^2} \cdot\xi \hspace{0.05cm}.$$
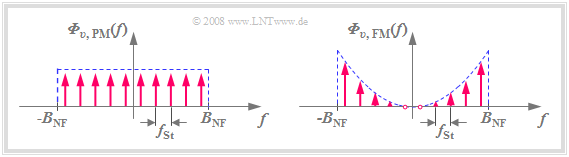
The graph illustrates:
- The noise power density ${\it Φ}_{v,\hspace{0.1cm}{\rm FM} }(f)$ is not white, unlike ${\it Φ}_{v,\hspace{0.1cm}{\rm PM} }(f)$.
- Rather, ${\it Φ}_{v,\hspace{0.1cm}{\rm FM} }(f)$ increases with $f^2$ towards the limits $(\pm B_{\rm NF} )$.
- When $f = 0$, ${\it Φ}_{v,\hspace{0.1cm}{\rm FM} }(f)$ has no noise components.
System comparison of AM, PM and FM with respect to noise
As explained in detail in the "Investigations at the AWGN channel" section and applied to amplitude modulation in the "Sink SNR and the performance parameter" section, we again consider the double-logarithmic plot of the sink SNR $ρ_v$ versus the performance parameter
- $$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}.$$
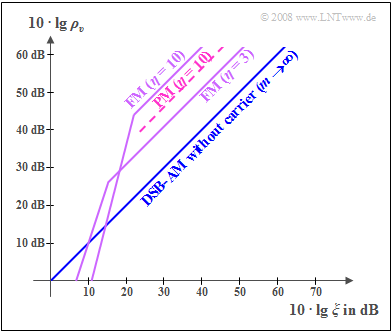
These curves, which are to be understood qualitatively, are to be interpreted as follows:
- The comparison curve shows »DSB–AM without a carrier« ⇒ modulation depth $m → ∞$. Here, $ρ_v = ξ$, and double-logarithmic representation also yields a $45^\circ$ straight line through the origin.
- The »FM curve« with $η = 3$ lies around $10 · \lg \ 13.5 ≈ 11.3 \ \rm dB$ above the AM curve. Visibly, the superior noise performance of frequency modulation can be explained by the fact that an additive noise component affects the position of the zero crossings less than it changes the amplitude values.
- When noise is strong and thus the performance parameter very small $(10 · \lg \ ξ ≤ 15 \ \rm dB)$, any kind of angle modulation $\rm (WM)$ is not recommended. Due to noise, zero crossings can then disappear completely and making their detection impossible. This is referred to as "WM threshold effect".
- With regard to noise, the greatest possible modulation index should be aimed for with any type of angle modulation. Like this, the FM curve for $η = 10$ is about $10.4 \ \rm dB$ above the curve for $η = 3$.
- However, it must be taken into account that a larger $η$ also requires a larger bandwidth or – for given channel bandwidth – causes stronger non-linear distortions.
- For the same modulation index, phase modulation $\rm (PM)$ is always $10 \cdot \lg \ 3 ≈ 4.8 \ \rm dB$ worse than frequency modulation $\rm (FM)$. This is one of the reasons why analog phase modulation is in practice of little importance. In contrast, the "Phase Shift Keying" $\rm (PSK)$ variant is used more frequently than "Frequency Shift Keying" $\rm (FSK)$ in digital modulation because of other advantages.
Pre-emphasis and de-emphasis
An important result of the last sections was that the sink SNR in frequency modulation $\rm (FM)$ corresponding to $\rho_{v } \approx 1.5 \cdot{\eta^2} \cdot\xi \hspace{0.05cm}$ depends quadratically on the modulation index by close approximation.
- However, since in frequency modulation the modulation index $η$ is inversely proportional to the frequency $f_{\rm N}$ of the source signal,
- the sink SNR also depends on $f_{\rm N}$.
This leads to the following consequences:
- If the source signal consists of several frequencies, the higher frequencies have a smaller modulation index $η$ after FM modulation than lower frequencies.
- This also means: The higher frequency components $($with smaller $η)$ are therefore noisier than lower frequencies, unless special measures are taken.
One such measure is a »pre-emphasis«.
- Here, higher frequencies are boosted by a high-pass filter network $H_{\rm PE}(f)$ which increases only their modulation index $η$.
- The transmit-side "pre-emphasis" must be reversed at the receiver by a $H_{\rm DE}(f) = 1/H_{\rm PE}(f)$ network. This lowering of the higher frequencies is called »de-emphasis«.
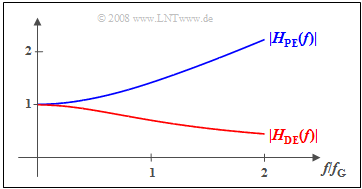
The diagram shows a possible example of the filter functions for
- pre-emphasis (blue) ⇒ $|H_{{\rm PE} } (f)| = \sqrt{1 + \left({f}/{f_{\rm G}}\right)^2}\hspace{0.05cm},$
- de-emphasis (red) ⇒ $|H_{{\rm DE} } (f)| = |H_{{\rm PE} } (f)|^{-1} \hspace{0.05cm}.$
Exercises for the chapter
Exercise 3.10: Noise Power Calculation
Exercise 3.10Z: Amplitude and Angle Modulation in Comparison
Exercise 3.11: Pre-Emphasis and De-Emphasis