Ideales und verzerrungsfreies System
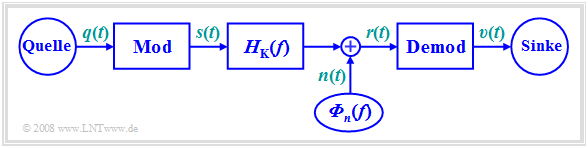
In allen nachfolgenden Kapiteln wird stets von folgendem Modell ausgegangen:
Die Aufgabe eines jeden Nachrichtenübertragungssystems besteht darin, an der räumlich entfernten Sinke ein Signal $υ(t)$ zur Verfügung zu stellen, das sich möglichst wenig vom Quellensignal $q(t)$ unterscheidet. Bei $υ(t) = q(t)$ würde man von einem idealen System sprechen.
In der Praxis werden sich die Signale $q(t)$ und $υ(t)$ stets unterscheiden, wofür es folgende Gründe gibt:
- Nichtideale Realisierung von Modulator und Demodulator,
- lineare Dämpfungs– und Phasenverzerrungen sowie Nichtlinearitäten,
- externe Störungen und stochastische Rauschprozesse,
- frequenzunabhängige Dämpfung und Laufzeit.
Ist nur die letztgenannte Einschränkung wirksam, so liegt ein verzerrungs– und rauschfreies System vor, und es gilt:
$$v(t) = \alpha \cdot q(t- \tau).$$
Durch den Dämpfungsfaktor $α$ ist das Sinkensignal $υ(t)$ gegenüber dem Quellensignal $q(t)$ nur „leiser”. Auch eine Laufzeit $τ$ ist oft tolerabel, zumindest bei einer unidirektionalen Übertragung. Dagegen wird bei einer bidirektionalen Kommunikation – zum Beispiel einem Telefonat – schon eine Laufzeit von 300 Millisekunden als sehr störend empfunden.
Signal–zu–Stör–Leistungsverhältnis (1)
Im allgemeinen Fall wird sich das Sinkensignal $υ(t)$ auch gegenüber $α · q(t – τ)$ unterscheiden, und es gilt für das Fehlersignal: $$\varepsilon (t) = v(t) - \alpha \cdot q(t- \tau) = \varepsilon_{\rm V} (t) + \varepsilon_{\rm St} (t).$$
Dieses setzt sich aus zwei Anteilen zusammen:
- den linearen und nichtlinearen Verzerrungen $ε_{\rm V}(t)$, die durch Modulator, Kanal und Demodulator hervorgerufen werden können und deterministisches Verhalten zeigen,
- der stochastischen Komponente $ε_{\rm St}(t)$, die von der HF–Störung $n(t)$ am Demodulatoreingang herrührt. Im Gegensatz zu $n(t)$ handelt es sich bei $ε_{\rm St}(t)$ um eine niederfrequente Störung.
Als Maß für die Qualität des Nachrichtensystems wird das Signal–zu–Stör–Leistungsverhältnis $ρ_υ$ an der Sinke als Quotient der Leistungen (Varianzen) von Nutzanteil $υ(t) – ε(t)$ und Störanteil $ε(t)$ definiert:
$$P_{v -\varepsilon} = \overline{[v(t)-\varepsilon(t)]^2} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int\limits_{0}^{ T_{\rm M}}
{[v(t)-\varepsilon(t)]^2 }\hspace{0.1cm}{\rm d}t,$$
$$P_{\varepsilon} = \overline{\varepsilon^2(t)} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int\limits_{0}^{ T_{\rm M}}
{\varepsilon^2(t) }\hspace{0.1cm}{\rm d}t$$
$$\Rightarrow \hspace{0.5cm}\rho_{v} = \frac{ P_{v -\varepsilon}}{P_{\varepsilon}} \hspace{0.05cm}.$$
Für die Leistung des Nutzanteils erhält man unabhängig von der Laufzeit $τ$: $$P_{v -\varepsilon} = \overline{[v(t)-\varepsilon(t)]^2} = \overline{\alpha^2 \cdot q^2(t - \tau)}= \alpha^2 \cdot P_{q}.$$ Hierbei bezeichnet $P_q$ die Leistung des Quellensignals $q(t)$: $$P_{q} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int\limits_{0}^{ T_{\rm M}} {q^2(t) }\hspace{0.1cm}{\rm d}t .$$ Damit erhält man: $$\rho_{v} = \frac{\alpha^2 \cdot P_{q}}{P_{\varepsilon}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}\rho_{v} = 10 \cdot {\rm lg} \hspace{0.15cm} \frac{\alpha^2 \cdot P_{q}}{P_{\varepsilon}} \hspace{0.05cm}.$$ Im Folgenden bezeichnen wir $ρ_υ$ kurz als das Sinken–SNR (Signal–to–Noise–Ratio) und 10 · lg $ρ_υ$ als den Sinken–Störabstand, der bei Verwendung des Zehner–Logarithmus (lg) in dB angegeben wird.
Signal–zu–Stör–Leistungsverhältnis (2)
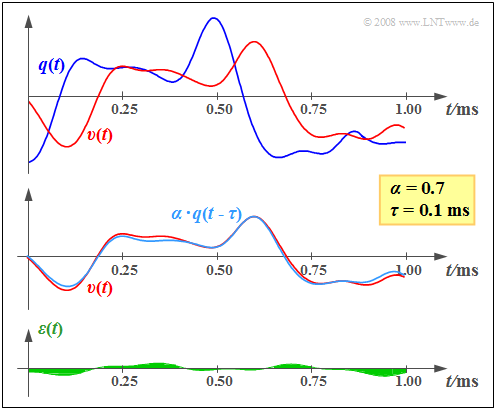
Nachfolgend sehen Sie einen beispielhaften Ausschnitt des (blauen) Quellensignals $q(t)$ und des (roten) Sinkensignals $υ(t)$, die sich deutlich voneinander unterscheiden.
Die mittlere Grafik macht jedoch deutlich, dass der wesentliche Unterschied zwischen $q(t)$ und $υ(t)$ auf den Dämpfungsfaktor $α =$ 0.7 und die Laufzeit $τ =$ 0.1 Millisekunden zurückzuführen ist.
Die untere Skizze zeigt das verbleibende Fehlersignal $ε(t) = υ(t) – α · q(t – τ)$ nach Korrektur von Dämpfung und Laufzeit. Der quadratische Mittelwert (Varianz) dieses Signals ist die Störleistung $P_ε$.
Zur Berechnung des Sinken–SNR $ρ_υ$ muss $P_ε$ in Bezug zur Nutzleistung $α^2 · P_q$ gesetzt werden. Diese ergibt sich als die Varianz des in der mittleren Grafik hellblau eingezeichneten Signals $α · q(t – τ)$. Mit den für diese Grafik vorausgesetzten Kenngrößen $$\alpha = 0.7\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\alpha^2 \approx 0.5, \hspace{0.2cm} P_{q} = 8\,{\rm V^2}, \hspace{0.2cm}{P_{\varepsilon}} = 0.04\,{\rm V^2}$$ ergibt sich das Sinken–SNR $ρ_υ$ ≈ 100 bzw. der Sinken–Störabstand 10 · lg $ρ_υ$ ≈ 20 dB.
Das Fehlersignal $ε(t)$ – und damit auch das Sinken–SNR $ρ_υ$ – berücksichtigt alle Unzulänglichkeiten des betrachteten Nachrichtenübertragungssystems (Verzerrungen, externe Störungen, Rauschen, usw.). Im Folgenden werden wir aus Darstellungsgründen die unterschiedlichen Effekte getrennt betrachten.