Contents
# OVERVIEW OF THE FIRST MAIN CHAPTER #
This first chapter serves as an »introduction to the whole topic«, which is covered by the nine books of the $\rm LNTwww$ series.
This chapter describes in detail:
- The »tasks and basic structure« of a transmission system,
- the »main functional units« $($source, transmitter, channel, receiver, sink$)$ of such a system, and finally
- a »classification of the signals« occurring in a transmission system according to several evaluation criteria:
»deterministic or stochastic, energy or power limited, continuous or discrete time, continuous or discrete value, analog or digital«.
At the end of the chapter follows a short summary about »Calculating with complex numbers«.
Message - Information - Signal
One distinguishes basically between the terms »message« and »information«, which are often used synonymously nowadays.
$\text{Example 1:}$ An e–mail from Mr. Maier to Mrs. Miller is always a »message«.
- For Mrs. Miller, however, receiving this e–mail only means an information gain if she learns something new.
- The »information« transmitted by a message therefore depends to a great extent on the knowledge level of the recipient.
- In practice, the information contained in a message is rather small, especially in the field of telephony.
The transmission of messages and their storage always requires an energetic or material carrier called »signal«. Physically the representation of a message is done by signals, which can be of very different nature.
Possible appearances are:
- Electrical signals $($e.g. current and voltage curves$)$,
- electromagnetic waves $($e.g. in radio transmission$)$,
- progression of pressure, temperature or other physical quantities,
- acoustic signals $($e.g. output signal of a loudspeaker$)$,
- optical signals $($e.g. output signal of a laser$)$.
$\text{Please note:}$
- The signals used for »$\text{data transmission}$« are usually time functions. This means that $($at least$)$ one of the signal parameters is dependent on the time parameter $t$. Such parameters for a signal tone are e.g. the amplitude $($»volume«$)$ and the frequency $($»pitch«$)$.
- For storing messages ⇒ »$\text{data storage}$« the time functions are often mapped to spatial functions of suitable physical quantities such as magnetization $($»magnetic band«$)$ or degree of blackening $($»film«$)$.
The set of all message signals can be cataloged by different criteria, as described in the chapter »Signal classification«.
Block diagram of a transmission system
In the following diagram a transmission system is shown schematically.
The individual system components have the following tasks:
- The »message source« returns the »source signal« $q(t)$, which shall be transmitted over the channel to the spatially distant sink. The source can be for example a computer, a radio station or a telephone participant.
- In most cases the source signal $q(t)$ itself is unsuitable for transmission and must first be converted into the signal $s(t)$ in a suitable manner. This process is called »modulation« and is performed by the »transmitter«. In the following, the signal $s(t)$ is called »transmitted signal«.
- During transmission over the »channel« the signal $s(t)$ is changed in its form. At the same time, interference and noise signals are added. The signal at the channel output and simultaneously at the receiver input is called the »received signal« $r(t)$.
- The »receiver« must undo the conversion made by the transmitter. If, for example, the low-frequency source signal $q(t)$ was converted to the higher-frequency transmitted signal $s(t)$ the receiver must also contain a »demodulator« and undo this conversion.
- The last block in the model above is the »message sink«. The »sink signal« $v(t)$ is like the source signal $q(t)$ low-frequency. In the ideal case should apply for all times: $v(t) = q(t)$. But in practice this can never be reached exactly $($due to the unavoidable noise$)$.
Message source
As examples for message sources and for the source signal $q(t)$ can be mentioned:
- Audio signals, e.g. speech or music,
- video signals, e.g. an analog television signal or an MPEG encoded streaming video,
- data signals, e.g. the data stream of a USB interface or an email on the Internet,
- measure signals, e.g. for control or regulation in a production process.
In general, a distinction is made between analog and digital sources. The description presented in this book apply equally to analog and digital signals. The basic differences between analog and digital signals are discussed in the chapter »Signal classification«, and clarified with examples throughout the $($German language$)$ learning video
- »Analoge und digitale Signale« ⇒ "Analog and Digital Signals".
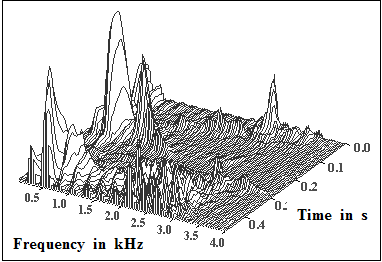
$\text{Example 2:}$ On the right you see the frequency-time representation of a speech signal:
- You can see the different frequency components in the kilohertz range at different times.
- By the way: This is a male speaker.
We thank Markus Kaindl[1], LNT/TUM, for providing the graphic.
Tasks of the transmitter
The essential task of the transmitter is to convert the source signal $q(t)$ into the transmitted signal $s(t)$ in such a way that it is adapted as well as possible to the transmission channel while maintaining the specified performance characteristics. For this purpose each transmitter contains corresponding »functional units« such as
- a transducer – e.g. a microphone for converting the physical quantity "pressure" $($acoustic wave$)$ into an electrical signal,
- a signal converter – for example from »analog« to »digital« using the components »sampling«, »quantization» and »PCM encoding»,
- an encoder for removing redundancy to data compression $($»source coding«$)$ or
for systematically adding redundancy, which can be used at the receiver for »error detection« and/or »error correction« $($»channel coding«$)$,
- a modulator for adaptation to the transmission channel – for example a frequency conversion by means of amplitude, phase or frequency modulation or the corresponding digital methods ASK, PSK, FSK.
Depending on the application, the »performance characteristics« mentioned above mean that very specific properties are required for signal transmission.
Such features are for example:
- »Power limitation« – due to the discussions on the topic "electrosmog" highly topical,
- »bandwidth efficiency« – the UMTS auction in 2000 has shown what magnitudes are involved,
- »distance« or »range« – unfavorable values increase the infrastructure costs,
- »transmission quality« – for example a high signal-to-noise ratio or a low error rate.
Transmission channel
The »transmission medium« with its physical properties plays an essential role in the feasibility of certain transmission properties.
Examples of transmission media are:
- Electrical cables, e.g. copper wire, twisted pair,
- coaxial cable, e.g. antenna line or cable network,
- fiber optic cables, e.g. multi-mode and single-mode fiber optic,
- radio channels, e.g. broadcasting, mobile and satellite radio.
$\text{Please note:}$ These transmission media are not ideal in practice and impair the transmission. That means:
The received signal $r(t)$ is different from the transmitted signal $s(t)$, possibly due to
- the channel attenuation,
- delays on the channel,
- linear and nonlinear distortions.
⇒ In addition, the channel transmission properties can change significantly over time $($»time variance«, example: mobile radio$)$.
⇒ Also »interfering signals« that occur during signal transmission must always be taken into account. The following are examples of these:
- Noise signals, e.g. resistance and semiconductor noise,
- pulse disturbances, e.g. from power lines, spark interference and discharges,
- adjacent channel interference $($cross-talk of other users, cross-modulation$)$.
⇒ You will find basic information about modeling the transmission channel in general and the simple »AWGN channel« in the the $($German language$)$ learning video
- »Eigenschaften des Übertragungskanals« ⇒ "Properties of the Transmission Channel".
Receiver - Message sink
As examples of the message sinks we can mention
- eye and ear of man,
- video recorder and call recorder,
- a smartphone that downloads a file from the Internet,
- a control system that processes received measurement signals.
To ensure that at least in the ideal case the sink signal $v(t)$ could coincide with the source signal $q(t)$ – in practice however never attainable – all measures taken on the transmission side must be reversed by the receiver.
Corresponding »functional units« of a receiver are:
- Transducer – e.g. a loudspeaker to convert an electric signal into an acoustic signal $($counterpart of the microphone$)$,
- signal reconstruction – e.g. the reconstruction of the analog signal from the digital samples $(\rm D/A$ converter ⇒ counterpart to an $\rm A/D$ converter$)$,
- channel decoder – for example with the possibility of error detection and error correction $($counterpart of the channel encoder$)$.
Another important task of the receiver is to eliminate as much as possible the signal distortions and noise that occur during transmission. The realization of such system components for transmitters and receivers is done by different electrical networks and assemblies.
Here too, some functional units can be named as examples:
- Amplifier, filter and equalizer,
- oscillators and nonlinear components for demodulation and synchronization,
- digital signal processing components and signal processors.
Signal distortions
It has already been mentioned that ideally $v(t) = q(t)$ should be valid. However, as with any real transmission channel $r(t) \neq s(t)$, the sink signal $v(t)$ will be different from the source signal $q(t)$. Here are some examples:
$\text{Definition:}$ One speaks of »noise«, if for the sink signal applies:
- \[ v(t)=q(t)+n(t).\]
- The additive noise component $n(t)$ is always of stochastic nature and usually has no relation to the source signal $q(t)$.
- Such a noise component is inevitable for every transmission.
$\text{Definition:}$ The transmission is »distortion–free«, if the sink signal is as follows:
- \[v(t)=\alpha \cdot q(t-\tau)+n(t).\]
In this case the sink signal differs from the source signal except for the noise component $n(t)$ only by
- the attenuation factor $\alpha$ $($same for all frequencies), and
- the delay time $\tau$ $($also the same for all frequencies$)$.
$\text{Definition:}$ If the equation $v(t)=\alpha \cdot q(t-\tau)+n(t)$ is not fulfilled, then there are »distortions«.
As described in the book »Linear and Time Invariant Systems« one distinguishes between
⇒ In this context we refer to the $($German language$)$ learning video
- »Lineare und nichtlineare Verzerrungen« ⇒ "Linear and nonlinear distortions".
Here again in slightly different words:
- The attenuation factor $\alpha$ only causes the signal $v(t)$ to be slightly »quieter« than $q(t)$; but both signals have the same shape.
- The delay $\tau$ causes the signal $v(t)$ to arrive at the receiver later than $q(t)$ was sent.
Both effects are not particularly disturbing for a »unidirectional transmission«:
For example, one can still speak of a live transmission if the television picture arrives delayed by $($a fraction of$)$ seconds.
However, with »bidirectional transmission«, a long runtime can lead to problems:
During a telephone conversation, the two interlocutors then interrupt each other.
$\text{Example 3:}$ The terms used here shall now be clarified by an image signal.
On the right you see as original image a color template with $291 × 218$ pixels and $24$ bit color depth. From the possible $2^{24} = 16\hspace{0.08cm} 777\hspace{0.08cm} 216$ colors only a few colors are used here.
⇒ In the lower left image, the signal is superposed with additive noise $n(t)$ which is perceived as "snow".
The lower right image shows the influence of $($nonlinear$)$ distortions, which lead to a distortion of both brightness values and color information at the selected setting of the CCD camera. You can see:
- In the marked field of the gray staircase, the brightness corresponds approximately to the original image $($above on the right $)$.
- On the other hand, other fields appear as too light or too dark or filled with missing colors.
- Noise effects play no role in the lower right image as opposed to the lower left image.
- These linear distortions are no longer detectable due to the strong nonlinear distortions.
Exercises for the chapter
Exercise 1.1Z: ISDN Connection
References
- ↑ Kaindl, M.: Kanalcodierung für Sprache und Daten in GSM-Systemen. Dissertation.
Lehrstuhl für Nachrichtentechnik, TU München. VDI Fortschritt-Berichte, Reihe 10, Nr. 764, 2005.