Difference between revisions of "Signal Representation/Spectrum Analysis"
| Line 6: | Line 6: | ||
}} | }} | ||
| − | ==Spectral | + | ==Spectral Leakage== |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | The term '''spectral leakage effect''' is used to describe the distortion of the spectrum of a periodic and thus temporally unlimited signal due to the implicit time limit of the Discrete Fourier Transform (DFT). This means that, for example, a spectrum analyser | |
| − | * | + | * fake frequency components that are not present in the time signal, and/or |
| − | * | + | *actually existing spectral components are hidden by side lobes}}. |
| − | + | The following $\text{example 1}$ will show that for a periodic signal the application of the [[Signal_Representation/Discrete_Fourier_Transform_(DFT)|discrete Fourier Transform]] (DFT) is not useful without additional measures. The quality of the spectral analysis - i.e. the correctness of the spectrum found - is mainly determined here by the (more or less successful) adaptation of the DFT parameters to the signal parameters at hand. | |
| − | * | + | *If the period $T_0$ of the signal is known, the duration $T_{\rm P}$ of the signal section used for the DFT should be an integer multiple of $T_0$ . However, the task of spectral analysis is precisely to find arbitrary signal components, so that knowledge of $T_0$ cannot generally be assumed. |
| − | * | + | *A measure to improve the spectral analysis is the windowing with a "suitable" time function $w(t)$. The product signal $x(t) \cdot w(t)$ is then analysed. |
| − | * | + | *A large number of such window functions $w(t)$ are known from the literature, which lead to good or less satisfactory results depending on the task. |
| − | + | On the next pages the spectral leakage effect will be illustrated by examples and the advantages and disadvantages of the different window functions will be discussed. So much up front: '''There is no "best" window function for all applications'''. | |
| + | {{GraueBox|TEXT= | ||
| − | + | $\text{Example 1:}$ | |
| − | $\text{ | + | The upper graph '''(a)''' from [Söd93]<ref name='Söd93'>Söder, G.: ''Modellierung, Simulation und Optimierung von Nachrichtensystemen.'' In: Berlin – Heidelberg: Springer, 1993.</ref>. shows the time-discrete signal $d(\nu)$ of a harmonic oscillation with frequency $f_0 = 125\,\text{ kHz}$ ⇒ period $T_0 = 8 \,{\rm µ s}$. The distance between two successive time samples in this example is chosen to be $T_{\rm A} = 1 \,{\rm µ s}$ . |
| − | |||
| − | + | On the right is shown in logarithmic form (in dB) the frequency discrete spectrum $\vert D(\mu) \vert$ after a DFT with $N = 32$ samples, from which the further DFT parameters result as follows: | |
| − | * | + | *Duration of the time segment: $T_{\rm P} = 32 \,{\rm µ s}$, |
| − | * | + | *gridding of the frequency axis: $f_{\rm A} = 31.25 \,\text{ kHz}$. |
| − | + | Since the interval width $T_{\rm P}$ captures an integer multiple of the period duration $T_0$ , the DFT delivers the correct result. The two Dirac functions lie exactly at $\pm4 \cdot f_{\rm A}$. | |
| − | [[File:P_ID1160__Sig_T_5_4_S1_neu.png|center|frame| | + | [[File:P_ID1160__Sig_T_5_4_S1_neu.png|center|frame|Example of Applying Spectral Analysis]] |
| − | + | If one measures an oscillation of frequency $f_0 = 109.375\,\text{ kHz}$ ⇒ period $T_0 = 9.14 \,{\rm µ s}$ corresponding to the graph below '''(b)''', significant distortions of the spectrum occur. | |
| − | * | + | *Since now $T_{\rm P}/T_0 = 3.5$ is no longer an integer, the periodic continuation of the time section causes phase jumps, in our example by $\pi$. |
| − | * | + | *The spectral range now no longer consists of two Dirac functions as in the example '''(a)''', but of an approximately "continuous" frequency function with the maximum near the actual signal frequency and a series of further parts, which are called '''side lobes''' .}} |
| − | == | + | ==Describing Windowing from a Control Theory Perspective== |
<br> | <br> | ||
| − | [[File:EN_Sig_T_5_4_S2.png|right|frame| | + | [[File:EN_Sig_T_5_4_S2.png|right|frame|Rectangular Window and Bartlett Windows]] |
| − | + | The occurrence of such unwanted side lobes is now to be explained in terms of systems theory using the following diagram. This graphic was also taken from the book [Söd93]<ref name='Söd93'>Söder, G.: ''Modellierung, Simulation und Optimierung von Nachrichtensystemen.'' In: Berlin – Heidelberg: Springer, 1993.</ref>. | |
| − | + | First consider the upper graph '''(a)''' for the '''rectangular window'''. | |
| − | * | + | *The time limit implicit in the DFT corresponds to the multiplication of the signal $x(t)$ by a rectangular–window function $w(t)$ of height $1$ and duration $T_{\rm P}$. The upper left image shows the discrete-time representation of this rectangular function with the normalised time variable $\nu= t/T_{\rm A}$: |
:$${w} (\nu) = \left\{ \begin{array}{c} 1 \\ | :$${w} (\nu) = \left\{ \begin{array}{c} 1 \\ | ||
| Line 58: | Line 58: | ||
\end{array}$$ | \end{array}$$ | ||
| − | * | + | *From the multiplication $y(t) = x(t) \cdot w(t)$ of the signal to be analysed $x(t)$ and the window function $w(t)$ follows for the spectral function $Y(f) = X(f) \ast W(f)$, where for rectangular window function with $f_{\rm A} = 1/T_{\rm P}$ holds (the function $W(f)$ is shown in logarithmic form in the upper right graph): |
:$$W(f) = T_{\rm P} \cdot {\rm si}(\pi \cdot f \cdot T_{\rm P}) = {1}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot {f}/{f_{\rm A}})\hspace{0.05cm}.$$ | :$$W(f) = T_{\rm P} \cdot {\rm si}(\pi \cdot f \cdot T_{\rm P}) = {1}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot {f}/{f_{\rm A}})\hspace{0.05cm}.$$ | ||
| − | * | + | *If all spectral components ofs $x(t)$ lie in the frequency grid $\mu \cdot f_{\rm A}$, the discrete frequency spectral values $D(\mu )$ remain unchanged by the convolution with $W(f)$ . |
| − | * | + | *Otherwise, convolution with $W(f)$ leads to distortions, since the zeros of the $\rm si$-function now no longer fit the discrete values of the input spectrum. |
| − | + | The discontinuities in the time domain caused by limitation and periodic continuation are reduced if, instead of the constant one weighting by the rectangle, the two edge areas of the window are weighted weaker than the centre. | |
| − | + | Consider the graph below '''(b)''' for the '''Bartlett window''' - also called triangular window: | |
| − | * | + | *The time-discrete description of the Bartlett window is with $\nu = t/T_{\rm A}$: |
:$${w} (\nu) = \left\{ \begin{array}{c} 1 - {2 \hspace{0.05cm} \cdot \hspace{0.05cm} |\nu|}/{N} \\ | :$${w} (\nu) = \left\{ \begin{array}{c} 1 - {2 \hspace{0.05cm} \cdot \hspace{0.05cm} |\nu|}/{N} \\ | ||
0 \\ \end{array} \right.\quad | 0 \\ \end{array} \right.\quad | ||
| Line 77: | Line 77: | ||
{\rm sonst} \hspace{0.05cm}. \\ | {\rm sonst} \hspace{0.05cm}. \\ | ||
\end{array}$$ | \end{array}$$ | ||
| − | * | + | *From this follows for the time-continuous window function $w(t)$ and the spectral representation $W(f)$: |
:$${w} (t) = \left\{ \begin{array}{c} 1 -{|t|}/{(T_{\rm P}/2)} \\ | :$${w} (t) = \left\{ \begin{array}{c} 1 -{|t|}/{(T_{\rm P}/2)} \\ | ||
0 \\ \end{array} \right.\hspace{0.05cm} | 0 \\ \end{array} \right.\hspace{0.05cm} | ||
| Line 86: | Line 86: | ||
\hspace{0.2cm}W(f) ={1}/({2f_{\rm A}})\cdot {\rm si}^2(\pi \cdot | \hspace{0.2cm}W(f) ={1}/({2f_{\rm A}})\cdot {\rm si}^2(\pi \cdot | ||
{f}/({2f_{\rm A}}))\hspace{0.05cm}.$$ | {f}/({2f_{\rm A}}))\hspace{0.05cm}.$$ | ||
| − | * | + | *Due to the lower weighting of the edge regions, which are particularly problematic with unbounded signals, the (logarithmically drawn) spectrum $W(f)$ has lower side lobes than the $\rm si$ function in the upper image, which leads to lower leakage components. |
| − | * | + | *The better suppression of the side lobes, however, comes at the cost of a noticeable reduction and broadening of the main lobe, limiting the resolving power of the Bartlett window compared to the rectangular windowing. |
| − | == | + | ==Special Window Functions== |
<br> | <br> | ||
| − | [[File:EN_Sig_T_5_4_S3.png|right|frame|Hanning-, Hamming- | + | [[File:EN_Sig_T_5_4_S3.png|right|frame|Hanning-, Hamming- and Kaiser-Bessel Windows]] |
| − | + | Now some frequently used [https://en.wikipedia.org/wiki/Window_function window functions], viz. | |
| − | * | + | *the Hanning window, |
| − | * | + | *the Hamming window, and |
| − | * | + | *the Kaiser-Bessel window |
| − | + | will be described by means of graphs and equations contained therein. For the running variable in the time domain, $-N/2 ≤ \nu < N/2$ always applies. | |
| − | '' | + | ''Notes:'' |
| − | * | + | *In the Kaiser-Bessel window, the functions in the time and frequency domain are each shown for $\alpha = 3.5$ . |
| − | * ${\rm I}_0(.)$ | + | * ${\rm I}_0(.)$ denotes the [https://en.wikipedia.org/wiki/Bessel_function modified zero-order Bessel function]. |
| − | * | + | *Further window functions such as the Blackman-Harris window, the [https://en.wikipedia.org/wiki/Raised-cosine_filter cosine rolloff window] (also called Tukey window) and many more can be found in the book [Söd93]<ref name='Söd93'>Söder, G.: ''Modellierung, Simulation und Optimierung von Nachrichtensystemen.'' In: Berlin – Heidelberg: Springer, 1993.</ref>. |
| − | + | The suitability of these window functions for various tasks of spectral analysis is mentioned on the next page. | |
<br clear=all> | <br clear=all> | ||
| − | == | + | ==Goodness criteria of window functions== |
<br> | <br> | ||
| − | [[File:EN_Sig_T_5_4_S4_neu.png|right|frame| | + | [[File:EN_Sig_T_5_4_S4_neu.png|right|frame|Compilation of Important Quality Criteria of Window Functions]] |
| − | + | The table shows quality criteria for the window functions described on the last pages. The selection of a suitable window function should be made according to the following aspects: | |
| − | * | + | *The '''minimum distance between main lobe and side lobes''' should be as large as possible to keep the influence of the leakage effect low and to improve the amplitude resolution. |
| − | * | + | *For reasons of good frequency selectivity, the '''6dB bandwidth''' should be small. If it is too large, a dominant spectral line will mask smaller components in the surrounding area. |
| − | * | + | *The '''maximum process loss''' (in dB) includes the maximum scaling error and the equivalent noise bandwidth. This value should in no case exceed $\text{3.7 dB}$ . |
| − | + | These most important quality criteria are highlighted in red in the adjacent table. | |
| − | *In | + | *In each row, rather favourable window functions are highlighted in green and rather unfavourable ones in grey. |
| − | * | + | *From the distribution of the green and grey areas it is already evident that the optimal window function does not exist. |
<br clear=all> | <br clear=all> | ||
| − | + | Now the quality criteria given in the table are described in more detail: | |
| − | * | + | *The larger the ''minimum main-to-side lobe distance'' ⇒ ratio of the main lobe to the highest side lobe, the better the amplitude resolution of a window function. For the rectangle this distance is, as expected, smallest $\text{(13 dB)}$. The best result is achieved with $\text{92 dB}$ the fourth-order Blackman-Harris window. |
| − | * | + | *However, since not only the highest but also all other side lobes contribute to the leakage effect, the '''side lobe drop''' is another measure for the resolving power. Of the given window functions, the Hanning window and the cosine rolloff window with rolloff $r = 0.5$ have the most favourable values in this respect $\text{(18 dB/octave)}$. |
| − | * | + | *The '''6 dB bandwidth''', which can be read from the logarithmised spectral function, is an important measure of the frequency resolving power. Two spectral components present in the signal at $f_1$ and $f_2$ can only be resolved if the difference $f_2 - f_1$ is greater than the $\text{6 dB}$-bandwidth of the window function used (see following right graph). |
[[File:EN_Sig_T_5_4_S4b.png|center|frame|Zur Verdeutlichung der $\text{6 dB}$-Bandbreite]] | [[File:EN_Sig_T_5_4_S4b.png|center|frame|Zur Verdeutlichung der $\text{6 dB}$-Bandbreite]] | ||
| − | * | + | *The '''window area''' of the function $w(t)$ at the same time gives the height $W(0)$ in the spectral domain. For all windows except the rectangle, a window area smaller than $1$ and thus an error in the amplitude of the DFT result results due to the suppression of the outer samples, which, however, can be completely corrected if $w(t)$ is known. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ |
| − | * | + | *A good compromise is the '''Hanning window''' (highlighted in blue in the table), which never scores "grey" with respect to the three main criteria (red markings). |
| − | * | + | *The '''Hamming window''' differs from this only slightly in the time domain, but considerably in the spectral domain. Thus, the side lobe drop per octave is only more $\text{6 dB}$ $($instead of $\text{18 dB})$.}} |
| − | == | + | ==Maximum process loss== |
<br> | <br> | ||
| − | + | This combined quality criterion considers the '''maximum scaling error''' as well as the (normalised) '''equivalent noise bandwidth'''. The maximum process loss is usually given in $\text{dB}$ and should be rather small according to its name: | |
:$$10 \cdot {\rm lg}\hspace{0.15cm}V_{\rm P}\hspace{0.15cm}{\rm (in}\hspace{0.15cm}{\rm dB)}= 20 \cdot {\rm lg}\hspace{0.15cm} | :$$10 \cdot {\rm lg}\hspace{0.15cm}V_{\rm P}\hspace{0.15cm}{\rm (in}\hspace{0.15cm}{\rm dB)}= 20 \cdot {\rm lg}\hspace{0.15cm} | ||
| Line 148: | Line 148: | ||
\frac{\int_{-\infty}^{\infty}|W(f)|^2\hspace{0.05cm}{\rm d}f}{f_{\rm A} \cdot |W(f=0)|^2} \hspace{0.05cm}.$$ | \frac{\int_{-\infty}^{\infty}|W(f)|^2\hspace{0.05cm}{\rm d}f}{f_{\rm A} \cdot |W(f=0)|^2} \hspace{0.05cm}.$$ | ||
| − | + | From the [[Signal_Representation/Spectrum_Analysis#G.C3.BCtekriterien_von_Fensterfunktionen|table]] it can be seen that $V_{\rm P}$ takes values between $\text{3 dB}$ and $\text{4 dB}$ for the window functions considered, where window functions with $V_{\rm P} > 3. 7 \,\text{dB}$ (rectangle, Blackman-Harris, Kaiser-Bessel) should not be used. However, it is precisely these that are best with regard to the main-to-side lobe distance. | |
| − | + | The two proportions are to be interpreted as follows: | |
| − | * | + | *The ''maximum scaling error'' is the ratio by which the amplitude determined with the DFT differs from the actual signal amplitude. The amplitude error due to a window area smaller than $1$ is assumed to be corrected. |
| − | * | + | *The wider the main lobe of the window function, the smaller this scaling error. The error is largest when the frequency $f_0$ of a harmonic oscillation lies midway between two DFT support points ⇒ quotient $|W(f = 0)| / |W(f = f_{\rm A}/2)|$. |
| − | * | + | *The ''equivalent noise bandwidth'' of the window function used - calculable as the width of the equal-area rectangle with respect to the magnitude square $|W(f)|^2$ of the spectral function - captures the disturbing influence of white noise and should be as small as possible. |
| − | * | + | *The smallest noise bandwidth results for the rectangle. All other window functions have a larger noise bandwidth and thus, in the presence of noise interference, also a (significantly) less favourable signal-to-noise power ratio. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ |
| − | + | The results of this section can be summarised as follows: | |
| − | * | + | *An ideal window function does not exist. Depending on the task (good amplitude or frequency resolution) different windows provide the best result in each case. It is therefore recommended that one always uses several window functions for spectral analysis or at least one window function with different parameters. |
| − | * | + | *A workable compromise with regard to all criteria is the '''Hamming window''', which only gives an unfavourable value for the side lobe drop $($only $\text{6 dB per octave})$ . Although the '''Hanning window''' differs only marginally from the Hamming window in the time domain, in the spectral domain (minimum distance between main lobe and side lobes) the difference between the two is considerable.}} |
| − | == | + | ==Exercises for The Chapter== |
<br> | <br> | ||
[[Aufgaben:Exercise 5.4: Comparison of Rectangular And Hanning Window |Exercise 5.4: Comparison of Rectangular And Hanning Window ]] | [[Aufgaben:Exercise 5.4: Comparison of Rectangular And Hanning Window |Exercise 5.4: Comparison of Rectangular And Hanning Window ]] | ||
Revision as of 18:46, 2 January 2021
Contents
Spectral Leakage
$\text{Definition:}$ The term spectral leakage effect is used to describe the distortion of the spectrum of a periodic and thus temporally unlimited signal due to the implicit time limit of the Discrete Fourier Transform (DFT). This means that, for example, a spectrum analyser
- fake frequency components that are not present in the time signal, and/or
- actually existing spectral components are hidden by side lobes
.
The following $\text{example 1}$ will show that for a periodic signal the application of the discrete Fourier Transform (DFT) is not useful without additional measures. The quality of the spectral analysis - i.e. the correctness of the spectrum found - is mainly determined here by the (more or less successful) adaptation of the DFT parameters to the signal parameters at hand.
- If the period $T_0$ of the signal is known, the duration $T_{\rm P}$ of the signal section used for the DFT should be an integer multiple of $T_0$ . However, the task of spectral analysis is precisely to find arbitrary signal components, so that knowledge of $T_0$ cannot generally be assumed.
- A measure to improve the spectral analysis is the windowing with a "suitable" time function $w(t)$. The product signal $x(t) \cdot w(t)$ is then analysed.
- A large number of such window functions $w(t)$ are known from the literature, which lead to good or less satisfactory results depending on the task.
On the next pages the spectral leakage effect will be illustrated by examples and the advantages and disadvantages of the different window functions will be discussed. So much up front: There is no "best" window function for all applications.
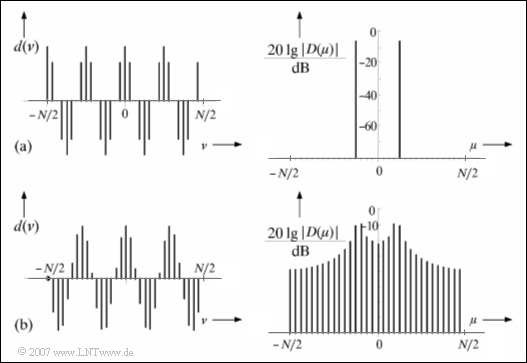
$\text{Example 1:}$ The upper graph (a) from [Söd93][1]. shows the time-discrete signal $d(\nu)$ of a harmonic oscillation with frequency $f_0 = 125\,\text{ kHz}$ ⇒ period $T_0 = 8 \,{\rm µ s}$. The distance between two successive time samples in this example is chosen to be $T_{\rm A} = 1 \,{\rm µ s}$ .
On the right is shown in logarithmic form (in dB) the frequency discrete spectrum $\vert D(\mu) \vert$ after a DFT with $N = 32$ samples, from which the further DFT parameters result as follows:
- Duration of the time segment: $T_{\rm P} = 32 \,{\rm µ s}$,
- gridding of the frequency axis: $f_{\rm A} = 31.25 \,\text{ kHz}$.
Since the interval width $T_{\rm P}$ captures an integer multiple of the period duration $T_0$ , the DFT delivers the correct result. The two Dirac functions lie exactly at $\pm4 \cdot f_{\rm A}$.
If one measures an oscillation of frequency $f_0 = 109.375\,\text{ kHz}$ ⇒ period $T_0 = 9.14 \,{\rm µ s}$ corresponding to the graph below (b), significant distortions of the spectrum occur.
- Since now $T_{\rm P}/T_0 = 3.5$ is no longer an integer, the periodic continuation of the time section causes phase jumps, in our example by $\pi$.
- The spectral range now no longer consists of two Dirac functions as in the example (a), but of an approximately "continuous" frequency function with the maximum near the actual signal frequency and a series of further parts, which are called side lobes .
Describing Windowing from a Control Theory Perspective
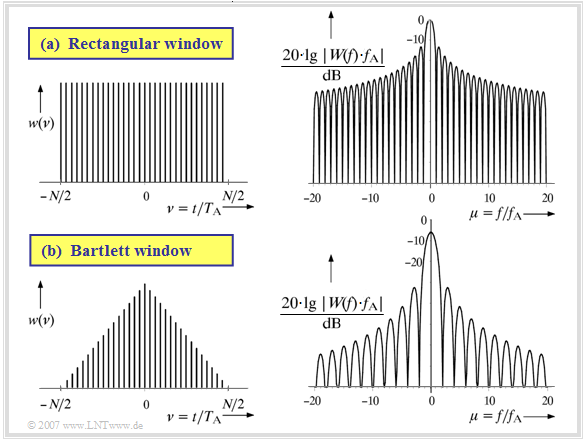
The occurrence of such unwanted side lobes is now to be explained in terms of systems theory using the following diagram. This graphic was also taken from the book [Söd93][1].
First consider the upper graph (a) for the rectangular window.
- The time limit implicit in the DFT corresponds to the multiplication of the signal $x(t)$ by a rectangular–window function $w(t)$ of height $1$ and duration $T_{\rm P}$. The upper left image shows the discrete-time representation of this rectangular function with the normalised time variable $\nu= t/T_{\rm A}$:
- $${w} (\nu) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ \\ \end{array}\begin{array}{*{20}c} -N/2 \le \nu < N/2 \hspace{0.05cm}, \\ {\rm sonst} \hspace{0.05cm}. \\ \end{array}$$
- From the multiplication $y(t) = x(t) \cdot w(t)$ of the signal to be analysed $x(t)$ and the window function $w(t)$ follows for the spectral function $Y(f) = X(f) \ast W(f)$, where for rectangular window function with $f_{\rm A} = 1/T_{\rm P}$ holds (the function $W(f)$ is shown in logarithmic form in the upper right graph):
- $$W(f) = T_{\rm P} \cdot {\rm si}(\pi \cdot f \cdot T_{\rm P}) = {1}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot {f}/{f_{\rm A}})\hspace{0.05cm}.$$
- If all spectral components ofs $x(t)$ lie in the frequency grid $\mu \cdot f_{\rm A}$, the discrete frequency spectral values $D(\mu )$ remain unchanged by the convolution with $W(f)$ .
- Otherwise, convolution with $W(f)$ leads to distortions, since the zeros of the $\rm si$-function now no longer fit the discrete values of the input spectrum.
The discontinuities in the time domain caused by limitation and periodic continuation are reduced if, instead of the constant one weighting by the rectangle, the two edge areas of the window are weighted weaker than the centre.
Consider the graph below (b) for the Bartlett window - also called triangular window:
- The time-discrete description of the Bartlett window is with $\nu = t/T_{\rm A}$:
- $${w} (\nu) = \left\{ \begin{array}{c} 1 - {2 \hspace{0.05cm} \cdot \hspace{0.05cm} |\nu|}/{N} \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ \\ \end{array}\begin{array}{*{20}c} -N/2 \le \nu < N/2 \hspace{0.05cm}, \\ {\rm sonst} \hspace{0.05cm}. \\ \end{array}$$
- From this follows for the time-continuous window function $w(t)$ and the spectral representation $W(f)$:
- $${w} (t) = \left\{ \begin{array}{c} 1 -{|t|}/{(T_{\rm P}/2)} \\ 0 \\ \end{array} \right.\hspace{0.05cm} \begin{array}{*{20}c} |t| \le T_{\rm P}/2\\ {\rm sonst} \\ \end{array}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm}W(f) ={1}/({2f_{\rm A}})\cdot {\rm si}^2(\pi \cdot {f}/({2f_{\rm A}}))\hspace{0.05cm}.$$
- Due to the lower weighting of the edge regions, which are particularly problematic with unbounded signals, the (logarithmically drawn) spectrum $W(f)$ has lower side lobes than the $\rm si$ function in the upper image, which leads to lower leakage components.
- The better suppression of the side lobes, however, comes at the cost of a noticeable reduction and broadening of the main lobe, limiting the resolving power of the Bartlett window compared to the rectangular windowing.
Special Window Functions
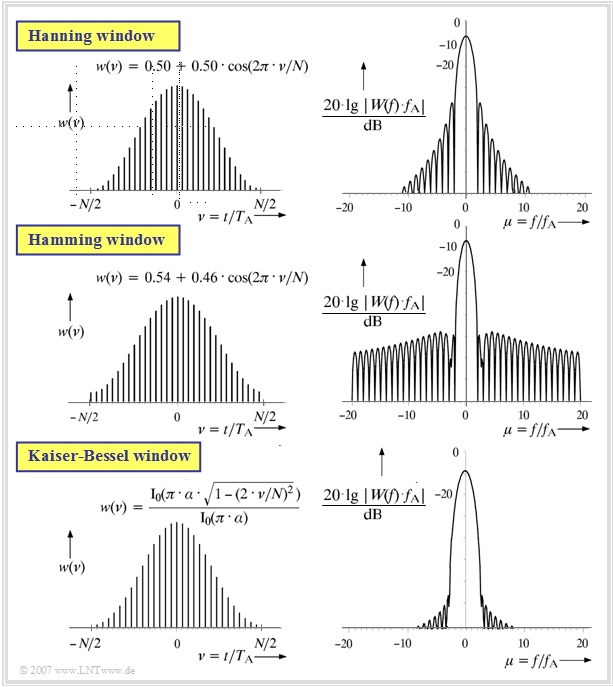
Now some frequently used window functions, viz.
- the Hanning window,
- the Hamming window, and
- the Kaiser-Bessel window
will be described by means of graphs and equations contained therein. For the running variable in the time domain, $-N/2 ≤ \nu < N/2$ always applies.
Notes:
- In the Kaiser-Bessel window, the functions in the time and frequency domain are each shown for $\alpha = 3.5$ .
- ${\rm I}_0(.)$ denotes the modified zero-order Bessel function.
- Further window functions such as the Blackman-Harris window, the cosine rolloff window (also called Tukey window) and many more can be found in the book [Söd93][1].
The suitability of these window functions for various tasks of spectral analysis is mentioned on the next page.
Goodness criteria of window functions
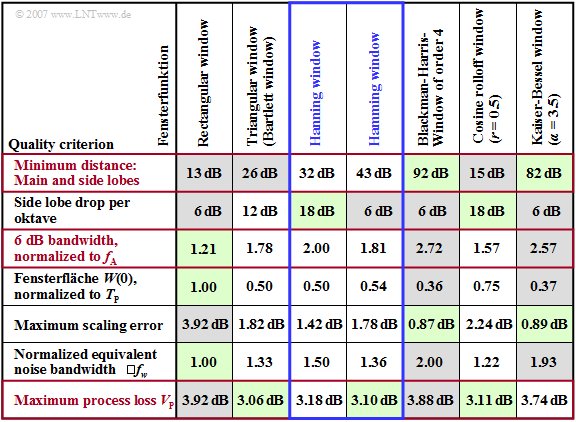
The table shows quality criteria for the window functions described on the last pages. The selection of a suitable window function should be made according to the following aspects:
- The minimum distance between main lobe and side lobes should be as large as possible to keep the influence of the leakage effect low and to improve the amplitude resolution.
- For reasons of good frequency selectivity, the 6dB bandwidth should be small. If it is too large, a dominant spectral line will mask smaller components in the surrounding area.
- The maximum process loss (in dB) includes the maximum scaling error and the equivalent noise bandwidth. This value should in no case exceed $\text{3.7 dB}$ .
These most important quality criteria are highlighted in red in the adjacent table.
- In each row, rather favourable window functions are highlighted in green and rather unfavourable ones in grey.
- From the distribution of the green and grey areas it is already evident that the optimal window function does not exist.
Now the quality criteria given in the table are described in more detail:
- The larger the minimum main-to-side lobe distance ⇒ ratio of the main lobe to the highest side lobe, the better the amplitude resolution of a window function. For the rectangle this distance is, as expected, smallest $\text{(13 dB)}$. The best result is achieved with $\text{92 dB}$ the fourth-order Blackman-Harris window.
- However, since not only the highest but also all other side lobes contribute to the leakage effect, the side lobe drop is another measure for the resolving power. Of the given window functions, the Hanning window and the cosine rolloff window with rolloff $r = 0.5$ have the most favourable values in this respect $\text{(18 dB/octave)}$.
- The 6 dB bandwidth, which can be read from the logarithmised spectral function, is an important measure of the frequency resolving power. Two spectral components present in the signal at $f_1$ and $f_2$ can only be resolved if the difference $f_2 - f_1$ is greater than the $\text{6 dB}$-bandwidth of the window function used (see following right graph).
- The window area of the function $w(t)$ at the same time gives the height $W(0)$ in the spectral domain. For all windows except the rectangle, a window area smaller than $1$ and thus an error in the amplitude of the DFT result results due to the suppression of the outer samples, which, however, can be completely corrected if $w(t)$ is known.
$\text{Conclusion:}$
- A good compromise is the Hanning window (highlighted in blue in the table), which never scores "grey" with respect to the three main criteria (red markings).
- The Hamming window differs from this only slightly in the time domain, but considerably in the spectral domain. Thus, the side lobe drop per octave is only more $\text{6 dB}$ $($instead of $\text{18 dB})$.
Maximum process loss
This combined quality criterion considers the maximum scaling error as well as the (normalised) equivalent noise bandwidth. The maximum process loss is usually given in $\text{dB}$ and should be rather small according to its name:
- $$10 \cdot {\rm lg}\hspace{0.15cm}V_{\rm P}\hspace{0.15cm}{\rm (in}\hspace{0.15cm}{\rm dB)}= 20 \cdot {\rm lg}\hspace{0.15cm} \frac{|W(f=0)|}{|W(f=f_{\rm A}/2)|} + 10 \cdot {\rm lg}\hspace{0.15cm} \frac{\int_{-\infty}^{\infty}|W(f)|^2\hspace{0.05cm}{\rm d}f}{f_{\rm A} \cdot |W(f=0)|^2} \hspace{0.05cm}.$$
From the table it can be seen that $V_{\rm P}$ takes values between $\text{3 dB}$ and $\text{4 dB}$ for the window functions considered, where window functions with $V_{\rm P} > 3. 7 \,\text{dB}$ (rectangle, Blackman-Harris, Kaiser-Bessel) should not be used. However, it is precisely these that are best with regard to the main-to-side lobe distance.
The two proportions are to be interpreted as follows:
- The maximum scaling error is the ratio by which the amplitude determined with the DFT differs from the actual signal amplitude. The amplitude error due to a window area smaller than $1$ is assumed to be corrected.
- The wider the main lobe of the window function, the smaller this scaling error. The error is largest when the frequency $f_0$ of a harmonic oscillation lies midway between two DFT support points ⇒ quotient $|W(f = 0)| / |W(f = f_{\rm A}/2)|$.
- The equivalent noise bandwidth of the window function used - calculable as the width of the equal-area rectangle with respect to the magnitude square $|W(f)|^2$ of the spectral function - captures the disturbing influence of white noise and should be as small as possible.
- The smallest noise bandwidth results for the rectangle. All other window functions have a larger noise bandwidth and thus, in the presence of noise interference, also a (significantly) less favourable signal-to-noise power ratio.
$\text{Conclusion:}$ The results of this section can be summarised as follows:
- An ideal window function does not exist. Depending on the task (good amplitude or frequency resolution) different windows provide the best result in each case. It is therefore recommended that one always uses several window functions for spectral analysis or at least one window function with different parameters.
- A workable compromise with regard to all criteria is the Hamming window, which only gives an unfavourable value for the side lobe drop $($only $\text{6 dB per octave})$ . Although the Hanning window differs only marginally from the Hamming window in the time domain, in the spectral domain (minimum distance between main lobe and side lobes) the difference between the two is considerable.
Exercises for The Chapter
Exercise 5.4: Comparison of Rectangular And Hanning Window
Exercise 5.4Z: On The Hanning Window