Difference between revisions of "Theory of Stochastic Signals/Cross-Correlation Function and Cross Power-Spectral Density"
| (33 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü= Random Variables with Statistical Dependence |
| − | |Vorherige Seite= | + | |Vorherige Seite=Power-Spectral Density |
| − | |Nächste Seite= | + | |Nächste Seite=Generalization to N-Dimensional Random Variables |
}} | }} | ||
| − | ==Definition | + | ==Definition of the cross-correlation function== |
| − | + | <br> | |
| + | In many engineering applications, one is interested in a quantitative measure to describe the statistical relatedness between different processes or between their pattern signals. One such measure is the "cross-correlation function", which is given here under the assumptions of "stationarity"' and "ergodicity". | ||
| − | {{Definition} | + | {{BlaueBox|TEXT= |
| − | :$$\varphi_{xy}(\tau)={\rm E} [{x(t)\cdot y(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\rm d \it t.$$ | + | $\text{Definition:}$ For the »'''cross-correlation function'''« $\rm (CCF)$ of two stationary and ergodic processes with the pattern functions $x(t)$ and $y(t)$ holds: |
| − | + | :$$\varphi_{xy}(\tau)={\rm E} \big[{x(t)\cdot y(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M} }\cdot\int^{T_{\rm M}/{\rm 2} }_{-T_{\rm M}/{\rm 2} }x(t)\cdot y(t+\tau)\,\rm d \it t.$$ | |
| + | *The first defining equation characterizes the expected value formation ("ensemble averaging"), | ||
| + | *while the second equation describes the "time averaging" over an (as large as possible) measurement period $T_{\rm M}$.}} | ||
| − | |||
| − | + | A comparison with the [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Auto-correlation_function_for_stationary_and_ergodic_processes|$\text{ACF definition}$]] shows many similarities. | |
| + | *Setting $y(t) = x(t)$, we get $φ_{xy}(τ) = φ_{xx}(τ)$, i.e., the auto-correlation function, | ||
| + | *for which, however, in our tutorial we mostly use the simplified notation $φ_x(τ)$. | ||
| − | {{ | + | {{GraueBox|TEXT= |
| − | [[File:P_ID434__Sto_T_4_6_S1neu.png |right|frame| | + | $\text{Example 1:}$ |
| − | + | We consider a random signal $x(t)$ with triangular auto-correlation function $φ_x(τ)$ ⇒ blue curve. This ACF shape results e.g. for | |
| − | + | [[File:P_ID434__Sto_T_4_6_S1neu.png |right|frame|Cross-correlation function of a binary signal]] | |
| − | + | ||
| + | *a binary signal with equally probable bipolar amplitude coefficients $(\pm1)$ | ||
| + | *and a rectangular basic pulse $g(t)$. | ||
| + | We consider a second signal $y(t) = \alpha \cdot x (t - t_{\rm 0})$, which differs from $x(t)$ only by an attenuation factor $(α =0.5)$ and a delay time $(t_0 = 3 \ \rm ms)$. | ||
| − | + | This attenuated and shifted signal has the auto-correlation function drawn in red: | |
:$$\varphi_{y}(\tau) = \alpha^2 \cdot \varphi_{x}(\tau) .$$ | :$$\varphi_{y}(\tau) = \alpha^2 \cdot \varphi_{x}(\tau) .$$ | ||
| − | + | The shift around $t_0$ is not seen in this auto-correlation function in contrast to the (green) cross-correlation function $\rm (CCF)$ for which the following relation holds: | |
| − | :$$\varphi_{xy}(\tau) = \alpha \cdot \varphi_{x}(\tau- t_{\rm 0}) .$$ | + | :$$\varphi_{xy}(\tau) = \alpha \cdot \varphi_{x}(\tau- t_{\rm 0}) .$$}} |
| − | |||
| − | == | + | ==Properties of the cross-correlation function== |
| − | + | <br> | |
| − | * | + | In the following, essential properties of the cross-correlation function $\rm (CCF)$ are composed. Important differences to the auto-correlation function $\rm (ACF)$ are: |
| − | :$$\varphi_{xy}(\tau)={\rm E} [{x(t)\cdot y(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\, \rm d \it t,$$ | + | *The formation of the cross-correlation function is »not commutative«. Rather, there are always two distinct functions, viz. |
| − | :$$\varphi_{yx}(\tau)={\rm E} [{y(t)\cdot x(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}y(t)\cdot x(t+\tau)\,\, \rm d \it t .$$ | + | :$$\varphi_{xy}(\tau)={\rm E} \big[{x(t)\cdot y(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\, \rm d \it t,$$ |
| − | * | + | :$$\varphi_{yx}(\tau)={\rm E} \big[{y(t)\cdot x(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}y(t)\cdot x(t+\tau)\,\, \rm d \it t .$$ |
| − | * | + | *There is a relationship between the two functions: $φ_{yx}(τ) = φ_{xy}(-τ)$. In [[Theory_of_Stochastic_Signals/Cross-Correlation_Function_and_Cross_Power-Spectral_Density#Definition_of_the_cross-correlation_function|$\text{Example 1}$]] of the last section, the second cross-correlation function $φ_{yx}(τ)$ would have its maximum at $τ = -3 \ \rm ms$. |
| − | * | + | *In general, the »maximum CCF« does not occur at $τ = 0$ $($exception: $y = α \cdot x)$ and the CCF value $φ_{xy}(τ = 0)$ does not have any special, physically interpretable meaning as in the ACF, where this value reflects the process power. |
| − | :$$\varphi_{xy}( \tau) | + | * For all $τ$-values, the »CCF magnitude« is less than or equal to the geometric mean of the two signal powers according to the [https://en.wikipedia.org/wiki/Cauchy%E2%80%93Schwarz_inequality $\text{Cauchy-Schwarz inequality}$]: |
| − | : | + | :$$\varphi_{xy}( \tau) \le \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)}.$$ |
| − | : | + | :In $\text{Example 1}$ in the last section, the equal sign applies: $\varphi_{xy}( \tau = t_{\rm 0}) = \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)} = \alpha \cdot \varphi_{x}( \tau = {\rm 0}) .$ |
| − | * | + | *If $x(t)$ and $y(t)$ do not contain a common periodic fraction, the »CCF limit« for $τ → ∞$ gives the product of both means: |
:$$\lim_{\tau \rightarrow \infty} \varphi _{xy} ( \tau ) = m_x \cdot m_y .$$ | :$$\lim_{\tau \rightarrow \infty} \varphi _{xy} ( \tau ) = m_x \cdot m_y .$$ | ||
| − | * | + | *If two signals $x(t)$ and $y(t)$ are »uncorrelated«, then $φ_{xy}(τ) ≡ 0$, that is, it is $φ_{xy}(τ) = 0$ for all values of $τ$. For example, this assumption is justified in most cases when considering a useful signal and a noise signal together. |
| − | * | + | *However, it should always be noted, that the CCF includes only the »linear statistical bindings« between the signals $x(t)$ and $y(t)$. Bindings of other types – such as for the case $y(t) = x^2(t)$ – are not taken into account in the CCF formation. |
| − | == | + | ==Applications of the cross-correlation function== |
| − | + | <br> | |
| − | + | The applications of the cross-correlation function in Communication systems are many. Here are some examples: | |
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 2:}$ In [[Modulation_Methods/Double-Sideband_Amplitude_Modulation|$\text{amplitude modulation}$]], but also in [[Modulation_Methods/Linear_Digital_Modulation#BPSK_.E2.80.93_Binary_Phase_Shift_Keying|$\text{BPSK systems}$]] ("Binary Phase Shift Keying"), the so-called [[Modulation_Methods/Synchronous_Demodulation|$\text{Synchronous Demodulator}$]] is often used for demodulation (resetting the signal to the original frequency range), whereby a carrier signal must also be added at the receiver, and this must be frequency and phase synchronous to the transmitter. | ||
| − | + | ⇒ If one forms the CCF between the received signal $r(t)$ and the carrier signal $z_{\rm E}(t)$ on the receiver side, the phase synchronous position between the two signals can be recognized by means of the CCF peak, and it can be readjusted in case of drifting apart.}} | |
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Example 3:}$ | ||
| + | The multiple access method [[Modulation_Methods/Spreading_Sequences_for_CDMA|$\text{CDMA}$]] ("Code Division Multiple Access") is used, for example, in the mobile radio standard [[Examples_of_Communication_Systems/General_Description_of_UMTS|$\text{UMTS}$]]. It requires strict phase synchronism, with respect to the added "pseudonoise sequences" at the transmitter ("band spreading") and at the receiver ("band compression"). | ||
| + | ⇒ This synchronization problem is also usually solved using the cross-correlation function.}} | ||
| − | |||
| − | == | + | {{GraueBox|TEXT= |
| − | + | $\text{Example 4:}$ | |
| + | The CCF can be used to determine whether or not a known signal $s(t)$ is present in a noisy received signal $r(t) = α - s(t - t_0) + n(t)$ and if so, at what time $t_0$ it occurs. | ||
| + | *From the calculated $t_0$ value, for example, a driving speed can be determined ("radar technique"). | ||
| + | *This task can also be solved with the "matched filter", which has many similarities with the CCF and is described in a [https://en.lntwww.de/Theory_of_Stochastic_Signals/Matched_Filter $\text{later chapter}$].}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 5:}$ In the so-called [[Digital_Signal_Transmission/Optimal_Receiver_Strategies#Matched_filter_receiver_vs._correlation_receiver|$\text{correlation receiver}$]], one uses the CCF for signal detection. Here one forms the cross-correlation function | ||
| + | * between the received signal $r(t)$ $($distorted by noise and possibly also by distortions$)$ | ||
| + | * and all possible transmitted signals $s_i(t)$, where for the control index $i = 1$, ... , $I$ shall hold. | ||
| − | |||
| + | ⇒ Deciding $N$ binary symbols together, then $I = {\rm 2}^N$. One then decides on the symbol sequence with the largest CCF value, achieving the minimum error probability according to the "maximum likelihood decision rule".}} | ||
| − | + | ==Cross power-spectral density== | |
| − | + | <br> | |
| − | + | For some applications it can be quite advantageous to describe the correlation between two random signals in the frequency domain. | |
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Definition:}$ | |
| − | |||
| − | |||
| − | : | ||
| − | {{ | + | The two »'''cross power-spectral densities'''« ${\it Φ}_{xy}(f)$ and ${\it Φ}_{yx}(f)$ result from the corresponding cross-correlation functions $\varphi_{xy}({\it \tau})$, resp. $\varphi_{yx}({\it \tau})$ by Fourier transform: |
| + | :$${\it \Phi}_{xy}(f)=\int^{+\infty}_{-\infty}\varphi_{xy}({\it \tau}) \cdot {\rm e}^{ {\rm -j}\pi f \tau} \rm d \it \tau, $$ | ||
| + | :$${\it \Phi}_{yx}(f)=\int^{+\infty}_{-\infty}\varphi_{yx}({\it \tau}) \cdot {\rm e}^{ {\rm -j}\pi f \tau} \rm d \it \tau.$$}} | ||
| − | |||
| − | + | The same relationship applies here as between | |
| + | *a deterministic signal $x(t)$ and its spectrum $X(f)$, | ||
| + | *the auto-correlation function ${\it φ}_x(τ)$ of an ergodic process $\{x_i(t)\}$ and the corresponding power-spectral density ${\it Φ}_x(f)$. | ||
| − | [[Aufgaben:4.14Z | + | |
| + | Similarly, the [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_second_Fourier_integral|$\text{inverse Fourier transform}$]] ⇒ "Second Fourier integral" describes here the transition from the frequency domain to the time domain. | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 6:}$ | ||
| + | We refer to [[Theory_of_Stochastic_Signals/Cross-Correlation_Function_and_Cross_Power_Density#Definition_of_the_cross-correlation_function|$\text{Example 1}$]] | ||
| + | [[File:P_ID772__Sto_T_4_6_S1neu.png |right|frame| For the definition of the cross-correlation function]] | ||
| + | *with the rectangular random variable $x(t)$ | ||
| + | * and the attenuated and shifted signal $y(t) = α - x(t - t_0)$. | ||
| + | |||
| + | |||
| + | ⇒ Since the auto-correlation function ${\it φ}_x(τ)$ is triangular, the power-spectral density ${\it Φ}_x(f)$ has a ${\rm sinc}^2$-shaped profile. | ||
| + | |||
| + | |||
| + | In general, what statements can we derive from this graph for the spectral functions? | ||
| + | #In $\text{Example 1}$ we found that the autocorrelation function ${\it φ}_y(τ)$ differs from ${\it φ}_x(τ)$ only by the constant factor $α^2$. | ||
| + | #It is clear that the power-spectral density ${\it Φ}_y(f)$ differs from ${\it \Phi}_x(f)$ also only by this constant factor $α^2$. Both spectral functions are real. | ||
| + | #In contrast, the cross power-spectral density has a complex functional: | ||
| + | :$${\it \Phi}_{xy}(f) ={\it \Phi}^\star_{yx}(f)= \alpha \cdot {\it \Phi}_{x}(f) \hspace{0.05cm}\cdot {\rm e}^{- {\rm j } \hspace{0.02cm}\pi f t_0}.$$}} | ||
| + | |||
| + | ==Exercises for the chapter== | ||
| + | <br> | ||
| + | [[Aufgaben:Exercise_4.14:_ACF_and_CCF_for_Square_Wave_Signals|Exercise 4.14: ACF and CCF for Square Wave Signals]] | ||
| + | |||
| + | [[Aufgaben:Exercise_4.14Z:_Echo_Detection|Exercise 4.14Z: Echo Detection]] | ||
{{Display}} | {{Display}} | ||
Latest revision as of 19:52, 21 December 2022
Contents
Definition of the cross-correlation function
In many engineering applications, one is interested in a quantitative measure to describe the statistical relatedness between different processes or between their pattern signals. One such measure is the "cross-correlation function", which is given here under the assumptions of "stationarity"' and "ergodicity".
$\text{Definition:}$ For the »cross-correlation function« $\rm (CCF)$ of two stationary and ergodic processes with the pattern functions $x(t)$ and $y(t)$ holds:
- $$\varphi_{xy}(\tau)={\rm E} \big[{x(t)\cdot y(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M} }\cdot\int^{T_{\rm M}/{\rm 2} }_{-T_{\rm M}/{\rm 2} }x(t)\cdot y(t+\tau)\,\rm d \it t.$$
- The first defining equation characterizes the expected value formation ("ensemble averaging"),
- while the second equation describes the "time averaging" over an (as large as possible) measurement period $T_{\rm M}$.
A comparison with the $\text{ACF definition}$ shows many similarities.
- Setting $y(t) = x(t)$, we get $φ_{xy}(τ) = φ_{xx}(τ)$, i.e., the auto-correlation function,
- for which, however, in our tutorial we mostly use the simplified notation $φ_x(τ)$.
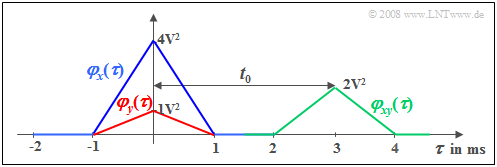
$\text{Example 1:}$ We consider a random signal $x(t)$ with triangular auto-correlation function $φ_x(τ)$ ⇒ blue curve. This ACF shape results e.g. for
- a binary signal with equally probable bipolar amplitude coefficients $(\pm1)$
- and a rectangular basic pulse $g(t)$.
We consider a second signal $y(t) = \alpha \cdot x (t - t_{\rm 0})$, which differs from $x(t)$ only by an attenuation factor $(α =0.5)$ and a delay time $(t_0 = 3 \ \rm ms)$.
This attenuated and shifted signal has the auto-correlation function drawn in red:
- $$\varphi_{y}(\tau) = \alpha^2 \cdot \varphi_{x}(\tau) .$$
The shift around $t_0$ is not seen in this auto-correlation function in contrast to the (green) cross-correlation function $\rm (CCF)$ for which the following relation holds:
- $$\varphi_{xy}(\tau) = \alpha \cdot \varphi_{x}(\tau- t_{\rm 0}) .$$
Properties of the cross-correlation function
In the following, essential properties of the cross-correlation function $\rm (CCF)$ are composed. Important differences to the auto-correlation function $\rm (ACF)$ are:
- The formation of the cross-correlation function is »not commutative«. Rather, there are always two distinct functions, viz.
- $$\varphi_{xy}(\tau)={\rm E} \big[{x(t)\cdot y(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\, \rm d \it t,$$
- $$\varphi_{yx}(\tau)={\rm E} \big[{y(t)\cdot x(t+\tau)}\big]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}y(t)\cdot x(t+\tau)\,\, \rm d \it t .$$
- There is a relationship between the two functions: $φ_{yx}(τ) = φ_{xy}(-τ)$. In $\text{Example 1}$ of the last section, the second cross-correlation function $φ_{yx}(τ)$ would have its maximum at $τ = -3 \ \rm ms$.
- In general, the »maximum CCF« does not occur at $τ = 0$ $($exception: $y = α \cdot x)$ and the CCF value $φ_{xy}(τ = 0)$ does not have any special, physically interpretable meaning as in the ACF, where this value reflects the process power.
- For all $τ$-values, the »CCF magnitude« is less than or equal to the geometric mean of the two signal powers according to the $\text{Cauchy-Schwarz inequality}$:
- $$\varphi_{xy}( \tau) \le \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)}.$$
- In $\text{Example 1}$ in the last section, the equal sign applies: $\varphi_{xy}( \tau = t_{\rm 0}) = \sqrt {\varphi_{x}( \tau = 0) \cdot \varphi_{y}( \tau = 0)} = \alpha \cdot \varphi_{x}( \tau = {\rm 0}) .$
- If $x(t)$ and $y(t)$ do not contain a common periodic fraction, the »CCF limit« for $τ → ∞$ gives the product of both means:
- $$\lim_{\tau \rightarrow \infty} \varphi _{xy} ( \tau ) = m_x \cdot m_y .$$
- If two signals $x(t)$ and $y(t)$ are »uncorrelated«, then $φ_{xy}(τ) ≡ 0$, that is, it is $φ_{xy}(τ) = 0$ for all values of $τ$. For example, this assumption is justified in most cases when considering a useful signal and a noise signal together.
- However, it should always be noted, that the CCF includes only the »linear statistical bindings« between the signals $x(t)$ and $y(t)$. Bindings of other types – such as for the case $y(t) = x^2(t)$ – are not taken into account in the CCF formation.
Applications of the cross-correlation function
The applications of the cross-correlation function in Communication systems are many. Here are some examples:
$\text{Example 2:}$ In $\text{amplitude modulation}$, but also in $\text{BPSK systems}$ ("Binary Phase Shift Keying"), the so-called $\text{Synchronous Demodulator}$ is often used for demodulation (resetting the signal to the original frequency range), whereby a carrier signal must also be added at the receiver, and this must be frequency and phase synchronous to the transmitter.
⇒ If one forms the CCF between the received signal $r(t)$ and the carrier signal $z_{\rm E}(t)$ on the receiver side, the phase synchronous position between the two signals can be recognized by means of the CCF peak, and it can be readjusted in case of drifting apart.
$\text{Example 3:}$ The multiple access method $\text{CDMA}$ ("Code Division Multiple Access") is used, for example, in the mobile radio standard $\text{UMTS}$. It requires strict phase synchronism, with respect to the added "pseudonoise sequences" at the transmitter ("band spreading") and at the receiver ("band compression").
⇒ This synchronization problem is also usually solved using the cross-correlation function.
$\text{Example 4:}$ The CCF can be used to determine whether or not a known signal $s(t)$ is present in a noisy received signal $r(t) = α - s(t - t_0) + n(t)$ and if so, at what time $t_0$ it occurs.
- From the calculated $t_0$ value, for example, a driving speed can be determined ("radar technique").
- This task can also be solved with the "matched filter", which has many similarities with the CCF and is described in a $\text{later chapter}$.
$\text{Example 5:}$ In the so-called $\text{correlation receiver}$, one uses the CCF for signal detection. Here one forms the cross-correlation function
- between the received signal $r(t)$ $($distorted by noise and possibly also by distortions$)$
- and all possible transmitted signals $s_i(t)$, where for the control index $i = 1$, ... , $I$ shall hold.
⇒ Deciding $N$ binary symbols together, then $I = {\rm 2}^N$. One then decides on the symbol sequence with the largest CCF value, achieving the minimum error probability according to the "maximum likelihood decision rule".
Cross power-spectral density
For some applications it can be quite advantageous to describe the correlation between two random signals in the frequency domain.
$\text{Definition:}$
The two »cross power-spectral densities« ${\it Φ}_{xy}(f)$ and ${\it Φ}_{yx}(f)$ result from the corresponding cross-correlation functions $\varphi_{xy}({\it \tau})$, resp. $\varphi_{yx}({\it \tau})$ by Fourier transform:
- $${\it \Phi}_{xy}(f)=\int^{+\infty}_{-\infty}\varphi_{xy}({\it \tau}) \cdot {\rm e}^{ {\rm -j}\pi f \tau} \rm d \it \tau, $$
- $${\it \Phi}_{yx}(f)=\int^{+\infty}_{-\infty}\varphi_{yx}({\it \tau}) \cdot {\rm e}^{ {\rm -j}\pi f \tau} \rm d \it \tau.$$
The same relationship applies here as between
- a deterministic signal $x(t)$ and its spectrum $X(f)$,
- the auto-correlation function ${\it φ}_x(τ)$ of an ergodic process $\{x_i(t)\}$ and the corresponding power-spectral density ${\it Φ}_x(f)$.
Similarly, the $\text{inverse Fourier transform}$ ⇒ "Second Fourier integral" describes here the transition from the frequency domain to the time domain.
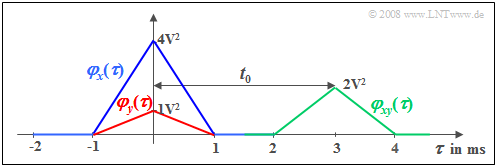
$\text{Example 6:}$ We refer to $\text{Example 1}$
- with the rectangular random variable $x(t)$
- and the attenuated and shifted signal $y(t) = α - x(t - t_0)$.
⇒ Since the auto-correlation function ${\it φ}_x(τ)$ is triangular, the power-spectral density ${\it Φ}_x(f)$ has a ${\rm sinc}^2$-shaped profile.
In general, what statements can we derive from this graph for the spectral functions?
- In $\text{Example 1}$ we found that the autocorrelation function ${\it φ}_y(τ)$ differs from ${\it φ}_x(τ)$ only by the constant factor $α^2$.
- It is clear that the power-spectral density ${\it Φ}_y(f)$ differs from ${\it \Phi}_x(f)$ also only by this constant factor $α^2$. Both spectral functions are real.
- In contrast, the cross power-spectral density has a complex functional:
- $${\it \Phi}_{xy}(f) ={\it \Phi}^\star_{yx}(f)= \alpha \cdot {\it \Phi}_{x}(f) \hspace{0.05cm}\cdot {\rm e}^{- {\rm j } \hspace{0.02cm}\pi f t_0}.$$
Exercises for the chapter
Exercise 4.14: ACF and CCF for Square Wave Signals
Exercise 4.14Z: Echo Detection