Exercise 4.10: Turbo Encoder for UMTS and LTE
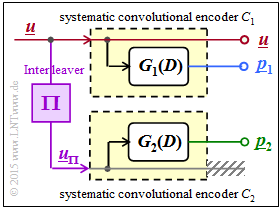
The mobile communications standards $\rm UMTS$ and $\rm LTE$ each use a turbo code that is largely identical to the encoder described in the "The Basics of Turbo Codes" chapter.
- The $1/n$ convolutional code is systematic, meaning that the encoded sequence $\underline{x}$ includes the information sequence $\underline{u}$ as a component.
- The parity-check sequences $\underline{p}_1$ and $\underline{p}_2$ are based on the same transfer function:
- $$G_1(D) = G_2(D) = G(D).$$
- $\underline{p}_1$ and $\underline{p}_2$ however, use different input sequences $\underline{u}$ and $\underline{u}_{\pi}$, respectively. Here, ${\rm \Pi}$ marks the interleaver, for UMTS and LTE mostly a $S$–random interleaver.
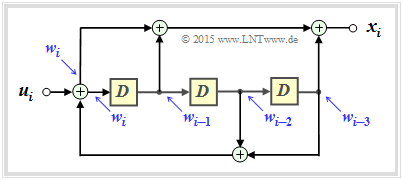
The main difference compared to the description in the theory part results from a different transfer function $G(D)$ given by the recursive filter structure drawn on the left.
Hints:
- The exercise belongs to the chapter "Basics of Turbo Codes".
- Knowledge is expected about
- For further guidance on how to do this, see $\text{Exercise 4.8}$ and $\text{Exercise 4.9}$.
- The information sequence $\underline{u}$ is partially specified by its $D$–transform for easier description in the subtasks. For example:
- $$\underline{u}= (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}\hspace{0.05cm} \text{...}\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = D+ D^2\hspace{0.05cm},$$
- $$\underline{u}= (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}\hspace{0.05cm} \text{...}\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = D+ D^8\hspace{0.05cm}.$$
Questions
Solution
(1) The code parameters are $k = 1$ and $n = 3$ ⇒ code rate $\underline{R = 1/3}$.
- The memory is $\underline{m = 3}$.
- The influence lengths result in $\nu = 1, \ \nu_2 = 4$ and $\nu_3 = 4$ ⇒ Total influence length $\underline{\nu = 9}$.
(2) As the comparison of the "recursive filter" on the data page with the "filter structure" in the theory section for fractional–rational $G(D)$, the proposed solution 1 is correct.
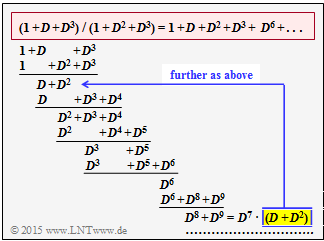
(3) Correct are the proposed solutions 2 and 3:
The upper graph illustrates the polynomial division $(1 + D + D^3) \ / \ (1 + D^2 + D^3)$. For explanation:
- Cancelled is the representation with the remainder $D^8 + D^9 = D^7 \cdot (D + D^2)$. Thus also holds:
- $$(D^8 + D^9) \hspace{0.05cm} /\hspace{0.05cm} (1+ D^2+ D^3 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} D^7 \cdot (D+ D^2+ D^3 + D^6) + {\rm remainder_2}$$
- After summarizing:
- $$G(D) = 1 + D + D^2 + D^3 + D^6 + D^8+ D^9+ D^{10} + D^{13} + \hspace{0.05cm}\text{ ... }\hspace{0.05cm} \hspace{0.05cm}. $$
- The $D$–inverse transform gives the proposed solution 2:
- $$\underline{g}= (\hspace{0.05cm}1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{ ... }\hspace{0.05cm})\hspace{0.05cm}. $$
- The impulse response continues to infinity ⇒ Solution proposal 3 is also correct.
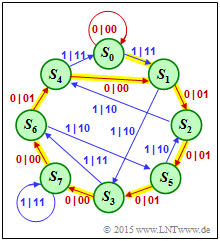
(4) The impulse response can be expressed as follows:
- $$\underline{g}= \Big (\hspace{0.03cm}1\hspace{0.03cm}, \big [ \hspace{0.03cm} 1\hspace{0.03cm}, \hspace{0.03cm} 1\hspace{0.03cm}, \hspace{0.03cm} 1\hspace{0.03cm}, \hspace{0.03cm} 0\hspace{0.03cm}, \hspace{0.03cm} 0\hspace{0.03cm}, \hspace{0.03cm} 1\hspace{0.03cm}, \hspace{0.03cm} 0\hspace{0.03cm} \big ]_{\rm per} \Big ) \hspace{0.15cm}\Rightarrow \hspace{0.15cm} \underline{P = 7} \hspace{0.05cm}. $$
- In the state transition diagram $($right$)$, the impulse response $\underline{g}$ is highlighted in yellow.
- The impulse response results as the parity-check sequence $\underline{p}$ for the information sequence $\underline{u} = (1, \, 0, \, 0, \, 0, \, 0, \, \text{ ... })$.
- The transitions in the diagram are labeled "$u_i\hspace{0.05cm}|\hspace{0.05cm}\underline{x}_i$", which is equivalent to "$u_i\hspace{0.05cm}|\hspace{0.05cm}u_i \hspace{0.05cm}p_i$".
- The parity-check sequence $\underline{p} \ (=$ impulse response $\underline{g})$ thus results from the respective second coder output symbol.
- The impulse response $\underline{g}$ is represented by the following states:
- $$S_0 → [S_1 → S_2 → S_5 → S_3 → S_7 → S_6 → S_4 ] → [S_1 → \ ... \ → S_4] → \ \text{ ... } $$
(5) The following graph shows the solution using the generator matrix $\mathbf{G}$. It holds $\underline{u} = (0, \, 1, \, 1, \, 0, \, 0, \, \text{ ... } )$.
It can be seen that solutions 1, 2 and 3 are correct:
- The present parity-check sequence $\underline{p}$ has the same period $P = 7$ as the impulse response $\underline{g}$.
- The Hamming weight of the $($limited$)$ input sequence is actually $w_{\rm H}(\underline{u}) = 2$.
- Proposition 4 is incorrect. Rather, for the semi–infinite output sequence: $w_{\rm H}(\underline{p}) → \infty$.
- In the transition diagram, the states
- $$S_0 → S_0 → S_1 → S_3 → S_7 → S_6 → S_4 → S_1$$
- are passed through first.
- This is followed $($infinitely often$)$ by the periodic portion
- $$S_1 → S_2 → S_5 → S_3 → S_7 → S_6 → S_4 → S_1.$$
(6) The last graph shows the solution for
- $$U(D) = D + D^8$$
- $$ \Rightarrow \hspace{0.3cm}\underline{u} = (0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 1, \, 0, \, 0, \, \text{ ... }).$$
- Correct are the proposed solutions 3 and 4:
- The input sequence $\underline{u}$ contains two "ones" and the output sequence $\underline{p}$ six "ones".
- From position 10 the output sequence is $\underline{p} \equiv\underline{0}$
⇒ proposals 1 and 2 therefore do not apply.
Further notes:
- For turbo codes, especially those input sequences $\underline{u}$ whose $D$–transforms are representable as $U(D) = f(D) \cdot [1 + D^{P}]$ are extremely unfavorable.
- They cause the error floor as seen on the "Performance of Turbo Codes" page in the theory section.
- $P$ indicates here the period of the impulse response $\underline{g}$. In our example $f(D) = D$ and $P = 7$.