Difference between revisions of "Information Theory/Discrete Sources with Memory"

Revision as of 13:27, 25 June 2021

A simple introductory example

$\text{Example 1:}$ At the beginning of the first chapter we have considered a memoryless message source with the symbol set $\rm \{A, \ B, \ C, \ D\}$ ⇒ $M = 4$ . An exemplary symbol sequence is shown again in the following figure as source $\rm Q1$ .

With the symbol probabilities $p_{\rm A} = 0.4 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.3 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.2 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.1\hspace{0.05cm}$ the entropy is

$$H \hspace{-0.05cm}= 0.4 \cdot {\rm log}_2\hspace{0.05cm}\frac {1}{0.4} + 0.3 \cdot {\rm log}_2\hspace{0.05cm}\frac {1}{0.3} + 0.2 \cdot {\rm log}_2\hspace{0.05cm}\frac {1}{0.2} + 0.1 \cdot {\rm log}_2\hspace{0.05cm}\frac {1}{0.1} \approx 1.84 \hspace{0.05cm}{\rm bit/symbol} \hspace{0.01cm}.$$

Due to the unequal symbol probabilities the entropy is smaller than $H_0 = \log_2 M = 2 \hspace{0.05cm} \rm bit/symbol$.

Quaternary source without/with memory

The source $\rm Q2$ is almost identical to the source $\rm Q1$, except that each individual symbol is output not only once, but twice in a row: $\rm A ⇒ AA$, $\rm B ⇒ BB$, and so on.

It is obvious that $\rm Q2$ has a smaller entropy (uncertainty) than $\rm Q1$.
Because of the simple repetition code, the entropy

$$H = 1.84/2 = 0.92 \hspace{0.05cm} \rm bit/symbol$$

has only half the size, although the occurrence probabilities have not changed.

$\text{Conclusion:}$ This example shows:

The entropy of a source with memory is smaller than the entropy of a memoryless source with equal symbol probabilities.
The statistical bindings within the sequence $〈 q_ν 〉$ have to be considered now,
namely the dependency of the symbol $q_ν$ from the predecessor symbols $q_{ν-1}$, $q_{ν-2}$, ...

Entropy with respect to two-tuples

We continue to look at the source symbol sequence $〈 q_1, \hspace{0.05cm} q_2,\hspace{0.05cm}\text{ ...} \hspace{0.05cm}, q_{ν-1}, \hspace{0.05cm}q_ν, \hspace{0.05cm}\hspace{0.05cm}q_{ν+1} .\hspace{0.05cm}\text{...} \hspace{0.05cm}〉$ and now consider the entropy of two successive source symbols.

All source symbols $q_ν$ are taken from an alphabet with the symbol set size $M$, so that for the combination $(q_ν, \hspace{0.05cm}q_{ν+1})$ there are exactly $M^2$ possible symbol pairs with the following combined probabilities:

$${\rm Pr}(q_{\nu}\cap q_{\nu+1})\le {\rm Pr}(q_{\nu}) \cdot {\rm Pr}( q_{\nu+1}) \hspace{0.05cm}.$$

From this, the compound entropy of two consecutive symbols can be computed:

$$H_2\hspace{0.05cm}' = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} \ \sum_{q_{\nu+1}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm} q_{\mu}\hspace{0.01cm} \}}\hspace{-0.1cm}{\rm Pr}(q_{\nu}\cap q_{\nu+1}) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu}\cap q_{\nu+1})} \hspace{0.4cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/two–tuple}) \hspace{0.05cm}.$$

The index "2" symbolizes that the entropy thus calculated refers to two-tuples.

To get the average information content per symbol, $H_2\hspace{0.05cm}'$ has to be divided in half:

$$H_2 = {H_2\hspace{0.05cm}'}/{2} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) \hspace{0.05cm}.$$

In order to achieve a consistent nomenclature, we now label the entropy defined in chapter Memoryless Message Sources with $H_1$:

$$H_1 = \sum_{q_{\nu}\hspace{0.05cm} \in \hspace{0.05cm}\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \}} {\rm Pr}(q_{\nu}) \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\nu})} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) \hspace{0.05cm}.$$

The index "1" is supposed to indicate that $H_1$ considers only the symbol probabilities and not statistical bindings between symbols within the sequence. With $H_0 = \log_2 \ M$ the following size relation results:

$$H_0 \ge H_1 \ge H_2 \hspace{0.05cm}.$$

With statistical independence of the sequence elements ⇒ $H_2 = H_1$.

The previous equations each indicate an "ensemble mean value". The probabilities required for the calculation of $H_1$ and $H_2$ can, however, also be calculated as time averages from a very long sequence or, more precisely, approximated by the corresponding relative frequencies.

Let us now illustrate the calculation of entropy approximations $H_1$ and $H_2$ with three examples.

Ternary symbol sequence and formation of two-tuples

$\text{Example 2:}$ We will first look at the sequence $〈 q_1$, ... , $q_{50} \rangle $ according to the graphic, where the sequence elements $q_ν$ originate from the alphabet $\rm \{A, \ B, \ C \}$ ⇒ the symbol set size is $M = 3$.

By time averaging over the $50$ symbols one gets the symbol probabilities $p_{\rm A} ≈ 0.5$, $p_{\rm B} ≈ 0.3$ and $p_{\rm C} ≈ 0.2$, with which one can calculate the first order entropy approximation:

$$H_1 = 0.5 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.5} + 0.3 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.3} + 0.2 \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{0.2} \approx \, 1.486 \,{\rm bit/symbol} \hspace{0.05cm}.$$

Due to the not equally probable symbols $H_1 < H_0 = 1.585 \hspace{0.05cm}. \rm bit/symbol$. As an approximation for the probabilities of two-tuples one gets from the above sequence:

$$\begin{align*}p_{\rm AA} \hspace{-0.1cm}& = \hspace{-0.1cm} 14/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm AB} = 8/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm AC} = 3/49\hspace{0.05cm}, \\\ p_{\rm BA} \hspace{-0.1cm}& = \hspace{0.07cm} 7/49\hspace{0.05cm}, \hspace{0.25cm}p_{\rm BB} = 2/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm BC} = 5/49\hspace{0.05cm}, \\\ p_{\rm CA} \hspace{-0.1cm}& = \hspace{0.07cm} 4/49\hspace{0.05cm}, \hspace{0.25cm}p_{\rm CB} = 5/49\hspace{0.05cm}, \hspace{0.2cm}p_{\rm CC} = 1/49\hspace{0.05cm}.\end{align*}$$

Please note that the $50$ sequence elements can only be formed from $49$ two-tuples $(\rm AA$, ... , $\rm CC)$ which are marked in different colors in the graphic.

The entropy approximation $H_2$ should actually be equal to $H_1$ since the given symbol sequence comes from a memoryless source.
Because of the short sequence length $N = 50$ and the resulting statistical inaccuracy, however, a smaller value results:

$$H_2 ≈ 1.39\hspace{0.05cm} \rm bit/symbol.$$

$\text{Example 3:}$ Now let us consider a memoryless binary source with equally probable symbols, i.e. there would be $p_{\rm A} = p_{\rm B} = 1/2$. The first twenty subsequent elements are $〈 q_ν 〉 =\rm BBAAABAABBBBBAAAABABAB$ ...

Because of the equally probable binary symbols $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$.
The compound probability $p_{\rm AB}$ of the combination $\rm AB$ is equal to $p_{\rm A} \cdot p_{\rm B} = 1/4$. Also $p_{\rm AA} = p_{\rm BB} = p_{\rm BA} = 1/4$.
This gives for the second entropy approximation

$$H_2 = {1}/{2} \cdot \big [ {1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 + {1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 +{1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 +{1}/{4} \cdot {\rm log}_2\hspace{0.1cm}4 \big ] = 1 \,{\rm bit/symbol} = H_1 = H_0 \hspace{0.05cm}.$$

Note: Due to the short length of the given sequence the probabilities are slightly different: $p_{\rm AA} = 6/19$, $p_{\rm BB} = 5/19$, $p_{\rm AB} = p_{\rm BA} = 4/19$.

$\text{Example 4:}$ The third sequence considered here results from the binary sequence of $\text{Example 3}$ by using a simple repeat code:

$$〈 q_ν 〉 =\rm BbBbAaAaAaBbAaAaBbBb \text{...} $$

The repeated symbols are marked by corresponding lower case letters. But it still applies $M=2$.
Because of the equally probable binary symbols, this also results in $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$.
As shown in Exercise 1.3 for the compound probabilities we obtain $p_{\rm AA}=p_{\rm BB} = 3/8$ and $p_{\rm AB}=p_{\rm BA} = 1/8$. Hence

$$\begin{align*}H_2 ={1}/{2} \cdot \big [ 2 \cdot {3}/{8} \cdot {\rm log}_2\hspace{0.1cm} {8}/{3} + 2 \cdot {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}8\big ] = {3}/{8} \cdot {\rm log}_2\hspace{0.1cm}8 - {3}/{8} \cdot{\rm log}_2\hspace{0.1cm}3 + {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}8 \approx 0.906 \,{\rm bit/symbol} < H_1 = H_0 \hspace{0.05cm}.\end{align*}$$

A closer look at the task at hand leads to the following conclusion:

The entropy should actually be $H = 0.5 \hspace{0.05cm} \rm bit/symbol$ (every second symbol does not provide new information)
The second entropy approximation $H_2 = 0.906 \hspace{0.05cm} \rm bit/symbol$ is much larger than the entropy $H$.
For the entropy determination, the second order approximation is not sufficient. Rather, one must consider larger contiguous blocks of $k > 2$ symbols.
In the following, such a block is referred to as "$k$–tuple".

Generalization to $k$-tuple and boundary crossing

For abbreviation we write using the compound probability $p_i^{(k)}$ for a $k$–tuple in general:

$$H_k = \frac{1}{k} \cdot \sum_{i=1}^{M^k} p_i^{(k)} \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{p_i^{(k)}} \hspace{0.5cm}({\rm unit\hspace{-0.1cm}: \hspace{0.1cm}bit/symbol}) \hspace{0.05cm}.$$

The control variable $i$ stands for one of the $M^k$ tuples.
The previously calculated approximation $H_2$ results with $k = 2$.

$\text{Definition:}$ The entropy of a discrete source with memory has the following limit:

$$H = \lim_{k \rightarrow \infty }H_k \hspace{0.05cm}.$$

For the entropy approximations $H_k$ the following relations apply $(H_0=\log_2 M)$:

$$H \le \text{...} \le H_k \le \text{...} \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$

The computational effort will increase with increasing $k$ except for a few special cases (see the following example) and depends on the symbol set size $M$ of course:

For the calculation of $H_{10}$ for a binary source $(M = 2)$ one must average over $2^{10} = 1024$ terms.
With each further increase of $k$ by $1$ the number of sum terms doubles.
In case of a quaternary source $(M = 4)$ it must already be averaged over $4^{10} = 1\hspace{0.08cm}048\hspace{0.08cm}576$ summation terms for the determination of $H_{10}$.
Considering that each of these $4^{10} =2^{20} >10^6$ $k$–tuple should occur in simulation/time averaging about $100$ times (statistical guideline) to ensure sufficient simulation accuracy, it follows that the sequence length should be in this case greater than $N = 10^8$.

$\text{Example 5:}$ We consider an alternating binary sequence ⇒ $〈 q_ν 〉 =\rm ABABABAB$ ... . Accordingly it holds that $H_0 = H_1 = 1 \hspace{0.1cm} \rm bit/symbol$.

In this special case, the $H_k$ approximation must be determined independently from $k$ by averaging only two compound probabilities:

$k = 2$: $p_{\rm AB} = p_{\rm BA} = 1/2$ ⇒ $H_2 = 1/2 \hspace{0.2cm} \rm bit/symbol$,
$k = 3$: $p_{\rm ABA} = p_{\rm BAB} = 1/2$ ⇒ $H_3 = 1/3 \hspace{0.2cm} \rm bit/symbol$,
$k = 4$: $p_{\rm ABAB} = p_{\rm BABA} = 1/2$ ⇒ $H_4 = 1/4 \hspace{0.2cm} \rm bit/symbol$.

The entropy of this alternating binary sequence is therefore

$$H = \lim_{k \rightarrow \infty }{1}/{k} = 0 \hspace{0.05cm}.$$

The result was to be expected, since the considered sequence has only minimal information, which does not affect the entropy end value $H$, namely:
"Does $\rm A$ occur at the even or the odd times?"

You can see that $H_k$ comes closer to this final value $H = 0$ very slowly: The twentieth entropy approximation still returns $H_{20} = 0.05 \hspace{0.05cm} \rm bit/symbol$.

$\text{Summary of the results of the last pages:}$

Generally it applies to the entropy of a message source:

$$H \le \text{...} \le H_3 \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$

A redundancy-free source exists if all $M$ symbols are equally probable and there are no statistical bindings within the sequence.
For these hold $(r$ denotes the relative redundancy $)$:

$$H = H_0 = H_1 = H_2 = H_3 = \text{...}\hspace{0.5cm} \Rightarrow \hspace{0.5cm} r = \frac{H - H_0}{H_0}= 0 \hspace{0.05cm}.$$

A memoryless source can be quite redundant $(r> 0)$. This redundancy then is solely due to the deviation of the symbol probabilities from the uniform distribution. Here the following relations are valid:

$$H = H_1 = H_2 = H_3 = \text{...} \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}0 \le r = \frac{H_1 - H_0}{H_0}< 1 \hspace{0.05cm}.$$

The corresponding condition for a source with memory is

$$ H <\text{...} < H_3 < H_2 < H_1 \le H_0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} 0 < r = \frac{H_1 - H_0}{H_0}\le1 \hspace{0.05cm}.$$

If $H_2 < H_1$, then $H_3 < H_2$, $H_4 < H_3$, etc. ⇒ In the general equation, the "≤" character must be replaced by the "<" character.
If the symbols are equally probable, then again $H_1 = H_0$, while $H_1 < H_0$ applies to symbols which are not equally probable.

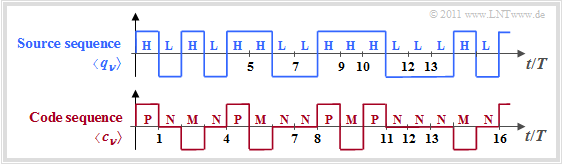
The entropy of the AMI code

In chapter Symbol-wise Coding with Pseudo-Ternary Codes of the book "Digital Signal Transmission", among other things, the AMI pseudo-ternary code is discussed.

Signals and symbol sequences for AMI code

This converts the binary sequence $〈 q_ν 〉$ with $q_ν ∈ \{ \rm L, \ H \}$ into the ternary sequence $〈 c_ν 〉$ with $q_ν ∈ \{ \rm M, \ N, \ P \}$.
The names of the source symbols stand for $\rm L$(ow) and $\rm H$(igh) and those of the code symbols for $\rm M$(inus), $\rm P$(lus), and $\rm N$(ull) ⇒ "Zero".

The coding rule of the AMI code ("Alternate Mark Inversion") is:

Each binary symbol $q_ν =\rm L$ is represented by the code symbol $c_ν =\rm N$ .
In contrast, $q_ν =\rm H$ alternates with $c_ν =\rm P$ and $c_ν =\rm M$ coded ⇒ name "Alternate Mark Inversion".
This special encoding adds redundancy with the sole purpose of ensuring that the code sequence does not contain a DC component.

However, we do not consider the spectral properties of the AMI code here, but interpret this code information-theoretically:

Based on the symbol set size $M = 3$ the decision content of the (ternary) code sequence is equal to $H_0 = \log_2 \ 3 ≈ 1.585 \hspace{0.05cm} \rm bit/symbol$. The first entropy approximation returns $H_1 = 1.5 \hspace{0.05cm} \rm bit/Symbol$, as shown in the following calculation:

$$p_{\rm H} = p_{\rm L} = 1/2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm N} = p_{\rm L} = 1/2\hspace{0.05cm},\hspace{0.2cm}p_{\rm M} = p_{\rm P}= p_{\rm H}/2 = 1/4\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_1 = 1/2 \cdot {\rm log}_2\hspace{0.1cm}2 + 2 \cdot 1/4 \cdot{\rm log}_2\hspace{0.1cm}4 = 1.5 \,{\rm bit/symbol} \hspace{0.05cm}.$$

Let's now look at two-tuples. With the AMI code, $\rm P$ cannot follow $\rm P$ and $\rm M$ cannot follow $\rm M$. The probability for $\rm NN$ is equal to $p_{\rm L} \cdot p_{\rm L} = 1/4$. All other (six) two-tuples occur with the probability $1/8$. From this follows for the second entropy approximation:

$$H_2 = 1/2 \cdot \big [ 1/4 \cdot {\rm log_2}\hspace{0.1cm}4 + 6 \cdot 1/8 \cdot {\rm log_2}\hspace{0.1cm}8 \big ] = 1,375 \,{\rm bit/symbol} \hspace{0.05cm}.$$

For the further entropy approximations $H_3$, $H_4$, ... and the actual entropy $H$ will apply:

$$ H < \hspace{0.05cm}\text{...}\hspace{0.05cm} < H_5 < H_4 < H_3 < H_2 = 1.375 \,{\rm bit/symbol} \hspace{0.05cm}.$$

Exceptionally in this example we know the actual entropy $H$ of the code symbol sequence $〈 c_ν 〉$: Since no new information is added by the coder and no information is lost, it is the same entropy $H = 1 \,{\rm bit/symbol} $ as the one of the redundancy-free binary sequence $〈 q_ν 〉$.

The Exercise 1.4 shows the considerable effort required to calculate the entropy approximation $H_3$. Moreover, $H_3$ still deviates significantly from the final value $H = 1 \,{\rm bit/symbol} $. A faster result is achieved if the AMI code is described by a Markov chain as explained in the next section.

Binary sources with Markov properties

Markov processes with $M = 2$ states

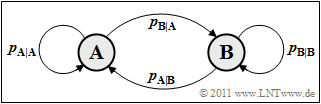
Sequences with statistical bindings between the sequence elements (symbols) are often modeled by Markov processes where we limit ourselves here to first-order Markov processes. First we consider a binary Markov process $(M = 2)$ with the states (symbols) $\rm A$ and $\rm B$.

On the right, you can see the transition diagram for a first-order binary Markov process however, only two of the four transfer probabilities given are freely selectable, for example

$p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = \rm Pr(A\hspace{0.01cm}|\hspace{0.01cm}B)$ ⇒ conditional probability that $\rm A$ follows $\rm B$ .
$p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}} = \rm Pr(B\hspace{0.01cm}|\hspace{0.01cm}A)$ ⇒ conditional probability that $\rm B$ follows $\rm A$ .

For the other two transition probabilities: $p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = 1- p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}$ and $p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} = 1- p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.05cm}.$

Due to the presupposed properties "Stationarity" and "Ergodicity" the following applies to the state or symbol probabilities:

$$p_{\rm A} = {\rm Pr}({\rm A}) = \frac{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}}{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}, \hspace{0.5cm}p_{\rm B} = {\rm Pr}({\rm B}) = \frac{p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}}{p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}.$$

These equations allow first information–theoretical statements about the Markov processes:

For $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$ the symbols are equally likely ⇒ $p_{\text{A}} = p_{\text{B}}= 0.5$. The first entropy approximation returns $H_1 = H_0 = 1 \hspace{0.05cm} \rm bit/symbol$, independent of the actual values of the (conditional) transition probabilities $p_{\text{A|B}}$ and $p_{\text{B|A}}$.
But the source entropy $H$ as the limit value $($for $k \to \infty)$ of the Entropy approximation of order $k$ ⇒ $H_k$ depends very much on the actual values of $p_{\text{A|B}}$ and $p_{\text{B|A}}$ and not only on their quotients. This is shown by the following example.

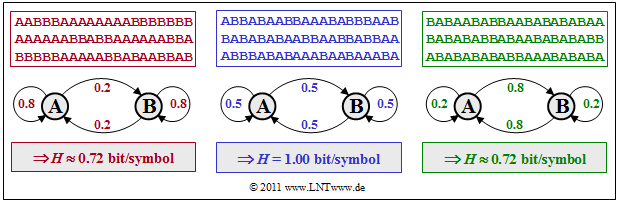
$\text{Example 6:}$ We consider three binary symmetric Markov sources that are represented by the numerical values of the symmetric transition probabilities $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} }$. For the symbol probabilities the following applies: $p_{\rm A} = p_{\rm B}= 0.5$, and the other transition probabilities have the values

Three examples of binary Markov sources with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} }$

$$p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 1 - p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}B} }.$$

The middle (blue) sequence with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.5$ has the entropy $H ≈ 1 \hspace{0.1cm} \rm bit/symbol$. That means: In this special case there are no statistical bindings within the sequence.

The left (red) sequence with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.2$ has less changes between $\rm A$ and $\rm B$. Due to statistical dependencies between neighboring symbols the entropy is now smaller: $H ≈ 0.72 \hspace{0.1cm} \rm bit/symbol$.

The right (green) symbol sequence with $p_{\rm {A\hspace{0.01cm}\vert\hspace{0.01cm}B} } = p_{\rm {B\hspace{0.01cm}\vert\hspace{0.01cm}A} } = 0.8$ has the exact same entropy $H ≈ 0.72 \hspace{0.1cm} \rm bit/symbol$ as the red sequence. Here you can see many regions with alternating symbols $($... $\rm ABABAB$ ... $)$.

This example is worth noting:

If you had not used the Markov properties of the red and green sequences, you would have reached the respective result $H ≈ 0.72 \hspace{0.1cm} \rm bit/symbol$ only after lengthy calculations.
The following pages show that for a source with Markov properties the final value $H$ can be determined from the entropy approximations $H_1$ and $H_2$ alone. Likewise, all entropy approximations $H_1$ and $H_2$ can also be calculated from $H_k$ for $k$–tuples in a simple manner ⇒ $H_3$, $H_4$, $H_5$, ... $H_{100}$, ...

Simplified entropy calculation for Markov sources

Markov processes with $M = 2$ states

We continue to assume the first-order symmetric binary Markov source. As on the previous page, we use the following nomenclature for

the transition probabilities ⇒ $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}}$, $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$, $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}A}}= 1- p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$, $p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}B}} = 1 - p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}}$,
the ergodic probabilities ⇒ $p_{\text{A}}$ and $p_{\text{B}}$,
the compound probabilities, for example ⇒ $p_{\text{AB}} = p_{\text{A}} - p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}}$.

We now compute the Entropy of a two-tuple (with the unit "bit/two-tuple"):

$$H_2\hspace{0.05cm}' = p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$

If one now replaces the logarithms of the products by corresponding sums of logarithms, one gets the result $H_2\hspace{0.05cm}' = H_1 + H_{\text{M}}$ with

$$H_1 = p_{\rm A} \cdot (p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A})\cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm A}} + p_{\rm B} \cdot (p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B})\cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm B}} = p_{\rm A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm A}} + p_{\rm B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_{\rm B}} = H_{\rm bin} (p_{\rm A})= H_{\rm bin} (p_{\rm B}) \hspace{0.05cm},$$

$$H_{\rm M}= p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm B} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm B} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$

$\text{Conclusion:}$ Thus the second entropy approximation (with the unit "bit/symbol") is:

$$H_2 = {1}/{2} \cdot {H_2\hspace{0.05cm}'} = {1}/{2} \cdot \big [ H_{\rm 1} + H_{\rm M} \big] \hspace{0.05cm}.$$

It is to be noted:

The first summand $H_1$ ⇒ first entropy approximation depends only on the symbol probabilities.
For a symmetrical Markov process ⇒ $p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}} = p_{\rm {B\hspace{0.01cm}|\hspace{0.01cm}A}} $ ⇒ $p_{\text{A}} = p_{\text{B}} = 1/2$ the result for this first summand is $H_1 = 1 \hspace{0.1cm} \rm bit/symbol$.
The second summand $H_{\text{M}}$ must be calculated according to the second of the two upper equations.
For a symmetrical Markov process you get $H_{\text{M}} = H_{\text{bin}}(p_{\rm {A\hspace{0.01cm}|\hspace{0.01cm}B}})$.

Now, this result is extended to the $k$–th entropy approximation. Here, the advantage of Markov sources over other sources is taken advantage of, that the entropy calculation for $k$–tuples is very simple. For each Markov source, the following applies

$$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M}\big ] \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_2 = {1}/{2} \cdot \big [ H_{\rm 1} + H_{\rm M} \big ]\hspace{0.05cm}, \hspace{0.3cm} H_3 ={1}/{3} \cdot \big [ H_{\rm 1} + 2 \cdot H_{\rm M}\big ] \hspace{0.05cm},\hspace{0.3cm} H_4 = {1}/{4} \cdot \big [ H_{\rm 1} + 3 \cdot H_{\rm M}\big ] \hspace{0.05cm},\hspace{0.15cm}{\rm usw.}$$

$\text{Conclusion:}$ With the boundary condition for $k \to \infty$, one obtains the actual source entropy

$$H = \lim_{k \rightarrow \infty} H_k = H_{\rm M} \hspace{0.05cm}.$$

From this simple result important insights for the entropy calculation follow:

For Markov sources it is sufficient to determine the entropy approximations $H_1$ and $H_2$. Thus, the entropy of a Markov source is

$$H = 2 \cdot H_2 - H_{\rm 1} \hspace{0.05cm}.$$

Through $H_1$ and $H_2$ all further entropy approximations $H_k$ are also fixed for $k \ge 3$ :

$$H_k = \frac{2-k}{k} \cdot H_{\rm 1} + \frac{2\cdot (k-1)}{k} \cdot H_{\rm 2} \hspace{0.05cm}.$$

However, these approximations are not very important. Mostly only the limit value $H$ is of interest. For sources without Markov properties the approximations $H_k$ are calculated only to be able to estimate this limit value, i.e. the actual entropy.

Notes:

In the Exercise 1.5 the above equations are applied to the more general case of an asymmetric binary source.
All equations on this page also apply to non-binary Markov sources $(M > 2)$ as shown on the next page.

Non-binary Markov sources

Ternary and quaternary first order Markov source

The following equations apply to each Markov source regardless of the symbol set size $M$:

$$H = 2 \cdot H_2 - H_{\rm 1} \hspace{0.05cm},$$

$$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H_{\rm M}\big ] \hspace{0.05cm},$$

$$ \lim_{k \rightarrow \infty} H_k = H \hspace{0.05cm}.$$

These equations allow the simple calculation of the entropy $H$ from the approximations $H_1$ and $H_2$.

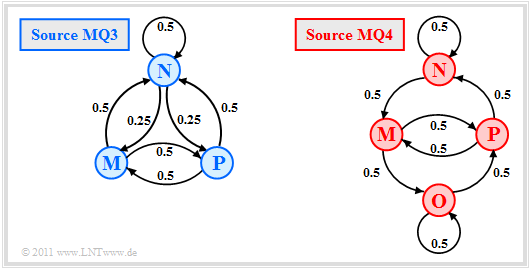
We now look at the transition diagrams sketched on the right:

A ternary Markov source $\rm MQ3$ $(M = 3$, blue coloring$)$, and
a quaternary Markov source $\rm MQ4$ $(M = 4$, red color$)$.

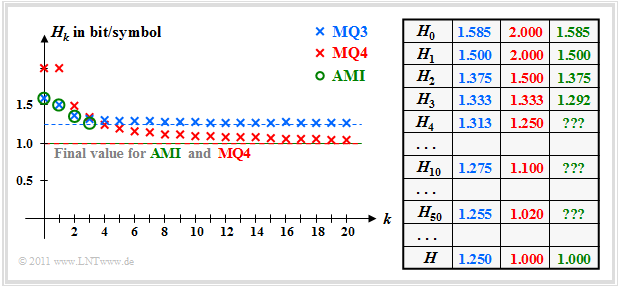
In Exercise 1.6 the entropy approximations $H_k$ and the total entropy $H$ are calculated as the limit of $H_k$ for $k \to \infty$ . The results are shown in the following figure. All entropies specified there have the unit "bit/symbol".

Entropies for $\rm MQ3$, $\rm MQ4$ and the $\rm AMI$ code

These results can be interpreted as follows:

For the ternary markov source $\rm MQ3$ the entropy approximations of $H_1 = 1.500$ above $H_2 = 1.375$ up to the limit $H = 1.250$ continuously decreasing. Because of $M = 3$ the decision content is $H_0 = 1.585$.
For the quaternary Markov source $\rm MQ4$ one receives $H_0 = H_1 = 2.000$ (since four equally probable states) and $H_2 = 1.5$. From the $H_1$- and $H_2$-values all entropy approximations $H_k$ and the final value $H = 1.000$ can be calculated.
The two models $\rm MQ3$ and $\rm MQ4$ were created during the attempt to calculate the AMI code to be described information–theoretically by Markov sources. The symbols $\rm M$, $\rm N$ and $\rm P$ stand for "minus", "zero" and "plus".
The entropy approximations $H_1$, $H_2$ and $H_3$ of the AMI code (green markers) were calculated in the Exercise 1.4. On the calculation of $H_4$, $H_5$, ... had to be omitted for reasons of effort. But the final value of $H_k$ for $k \to \infty$ ⇒ $H = 1.000$ is known.
You can see that the Markov model $\rm MQ3$ for $H_0 = 1.585$, $H_1 = 1.500$ and $H_2 = 1.375$ yields exactly the same numerical values as the AMI code. On the other hand $H_3$ ⇒ $(1.333$ instead of $1.292)$ and especially the final value $H$ ⇒ $(1.250$ compared to $1.000)$.
The model $\rm MQ4$ $(M = 4)$ differs from the AMI code $(M = 3)$ with respect to the decision content $H_0$ and also with respect to all entropy approximations $H_k$. Nevertheless, $\rm MQ4$ is the more suitable model for the AMI code, since the final value $H = 1,000$ is the same.
The model $\rm MQ3$ yields entropy values that are too large, since the sequences $\rm PNP$ and $\rm MNM$ are possible here, which cannot occur in the AMI code. Already with the approximation $H_3$ the difference is slightly noticeable, in the final value $H$ even clearly $(1.25$ instead of $1)$.

In the model $\rm MQ4$ the state "Zero" was split into two states $\rm N$ and $\rm O$ (see upper right figure on this page):

Here applies to the state $\rm N$: The current binary symbol $\rm L$ is encoded with the amplitude value $0$ (zero), as per the AMI rule. The next occurring $\rm H$ symbol, on the other hand, is displayed as $-1$ (minus), because the last symol $\rm H$ was encoded as $+1$ (plus).
Also with the state $\rm O$ the current binary symbol $\rm L$ is represented with the ternary value $0$. In contrast to the state $\rm N$ however, the next occurring $\rm H$ symbol is now encoded as $+1$ (plus) since the last $\rm H$ symbol was encoded as $-1$ (minus).

$\text{Conclusion:}$

The $\rm MQ4$ output sequence actually follows the rules of the AMI code and has entropy $H = 1.000 \hspace{0.15cm} \rm bit/symbol$.
But because of the new state $\rm O$ now $H_0 = 2.000 \hspace{0.15cm} \rm bit/symbol$ $($against $1.585 \hspace{0.15cm} \rm bit/symbol)$ is clearly too large.
Also all $H_k$ approximations are larger than with the AMI code. First for $k \to \infty$ the model $\rm MQ4$ and the AMI code match exactly: $H = 1.000 \hspace{0.15cm} \rm bit/symbol$.

Exercises for the chapter

Exercise 1.3: Entropy Approximations

Exercise 1.4: Entropy Approximations for the AMI Code

Exercise 1.4Z: Entropy of the AMI Code

Exercise 1.5: Binary Markov Source

Exercise 1.5Z: Symmetrical Markov Source

Exercise 1.6: Non-Binary Markov Sources

Exercise 1.6Z:Ternary Markov Source

@@ Line 18: / Line 18: @@
   \hspace{0.01cm}.$$
-Due to the unequal symbol probabilities the entropy is smaller than the decision content&nbsp; $H_0 = \log_2 M = 2 \hspace{0.05cm}. \rm bit/symbol$.
+Due to the unequal symbol probabilities the entropy is smaller than&nbsp; $H_0 = \log_2 M = 2 \hspace{0.05cm} \rm bit/symbol$.
 [[File:EN_Inf_T_1_2_S1a.png|right|frame|Quaternary source without/with memory]]