Difference between revisions of "Channel Coding/Decoding of Convolutional Codes"
| Line 30: | Line 30: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Conclusion:}$ Given a digital channel model (for example, the BSC model), the Viterbi algorithm searches from all possible code sequences $\underline{x}\hspace{0. 05cm}'$ the sequence $\underline{z}$ with the minimum Hamming distance $d_{\rm H}(\underline{x}\hspace{0.05cm}', \underline{y})$ to the receiving sequence $\underline{y}$: | + | $\text{Conclusion:}$ Given a digital channel model (for example, the BSC model), the Viterbi algorithm searches from all possible code sequences $\underline{x}\hspace{0.05cm}'$ the sequence $\underline{z}$ with the minimum Hamming distance $d_{\rm H}(\underline{x}\hspace{0.05cm}', \underline{y})$ to the receiving sequence $\underline{y}$: |
:<math>\underline{z} = {\rm arg} \min_{\underline{x}\hspace{0.05cm}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} d_{\rm H}( \underline{x}\hspace{0.05cm}'\hspace{0.02cm},\hspace{0.02cm} \underline{y} ) | :<math>\underline{z} = {\rm arg} \min_{\underline{x}\hspace{0.05cm}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} d_{\rm H}( \underline{x}\hspace{0.05cm}'\hspace{0.02cm},\hspace{0.02cm} \underline{y} ) | ||
| Line 37: | Line 37: | ||
This also means: The Viterbi algorithm satisfies the [[Channel_Coding/Channel_Models_and_Decision_Structures#Criteria_.C2.BBMaximum-a-posteriori.C2.AB_and_.C2.BBMaximum-Likelihood.C2.AB| "maximum likelihood criterion"]].}}<br> | This also means: The Viterbi algorithm satisfies the [[Channel_Coding/Channel_Models_and_Decision_Structures#Criteria_.C2.BBMaximum-a-posteriori.C2.AB_and_.C2.BBMaximum-Likelihood.C2.AB| "maximum likelihood criterion"]].}}<br> | ||
| − | == | + | == Preliminary remarks on the following decoding examples == |
<br> | <br> | ||
| − | [[File:P ID2652 KC T 3 4 S2 v1.png|right|frame|Trellis | + | [[File:P ID2652 KC T 3 4 S2 v1.png|right|frame|Trellis for decoding the received sequence $\underline{y}$|class=fit]] |
| − | + | The following '''prerequisites''' apply to all examples in this chapter: | |
| − | *Standard | + | *Standard convolutional encoder: Rate $R = 1/2$, Memory $m = 2$; |
| − | * | + | *transfer function matrix: $\mathbf{G}(D) = (1 + D + D^2, 1 + D^2)$; |
| − | * | + | *Length of information sequence: $L = 5$; |
| − | * | + | *Consideration of termination: $L\hspace{0.05cm}' = 7$; |
| − | * | + | *Length of sequences $\underline{x}$ and $\underline{y}$ : $14$ bits each; |
| − | * | + | *Distribution according to $\underline{y} = (\underline{y}_1, \ \underline{y}_2, \ \text{...} \ , \ \underline{y}_7)$ <br>⇒ bit pairs $\underline{y}_i ∈ \{00, 01, 10, 11\}$; |
| − | *Viterbi | + | *Viterbi decoding using trellis diagram: |
| − | :: | + | ::red arrow ⇒ hypothesis $u_i = 0$, |
| − | :: | + | ::blue arrow ⇒ hypothesis $u_i = 1$; |
| − | * | + | *hypothetical code sequence $\underline{x}_i\hspace{0.01cm}' ∈ \{00, 01, 10, 11\}$; |
| − | * | + | *all hypothetical quantities with apostrophe. |
<br clear=all> | <br clear=all> | ||
| − | + | We always assume that the Viterbi decoding is done at the [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding| Hamming distance]] $d_{\rm H}(\underline{x}_i\hspace{0. 01cm}', \ \underline{y}_i)$ between the received word $\underline{y}_i$ and the four possible codewords $x_i\hspace{0.01cm}' ∈ \{00, 01, 10, 11\}$ is based. We then proceed as follows: | |
| − | *In | + | *In the still empty circles the error value ${\it \Gamma}_i(S_{\mu})$ of the states $S_{\mu} (0 ≤ \mu ≤ 3)$ at the time points $i$ are entered. The initial value is always ${\it \Gamma}_0(S_0) = 0$. |
| − | * | + | *The error values for $i = 1$ and $i = 2$ are given by |
::<math>{\it \Gamma}_1(S_0) =d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_1 \big ) \hspace{0.05cm}, \hspace{2.38cm}{\it \Gamma}_1(S_1) = d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_1 \big ) \hspace{0.05cm},</math> | ::<math>{\it \Gamma}_1(S_0) =d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_1 \big ) \hspace{0.05cm}, \hspace{2.38cm}{\it \Gamma}_1(S_1) = d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_1 \big ) \hspace{0.05cm},</math> | ||
::<math>{\it \Gamma}_2(S_0) ={\it \Gamma}_1(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big )\hspace{0.05cm}, \hspace{0.6cm}{\it \Gamma}_2(S_1) = {\it \Gamma}_1(S_0)+ d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big ) \hspace{0.05cm},\hspace{0.6cm}{\it \Gamma}_2(S_2) ={\it \Gamma}_1(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big )\hspace{0.05cm}, \hspace{0.6cm}{\it \Gamma}_2(S_3) = {\it \Gamma}_1(S_1)+ d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big ) \hspace{0.05cm}.</math> | ::<math>{\it \Gamma}_2(S_0) ={\it \Gamma}_1(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big )\hspace{0.05cm}, \hspace{0.6cm}{\it \Gamma}_2(S_1) = {\it \Gamma}_1(S_0)+ d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big ) \hspace{0.05cm},\hspace{0.6cm}{\it \Gamma}_2(S_2) ={\it \Gamma}_1(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big )\hspace{0.05cm}, \hspace{0.6cm}{\it \Gamma}_2(S_3) = {\it \Gamma}_1(S_1)+ d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big ) \hspace{0.05cm}.</math> | ||
| − | * | + | *From $i = 3$ the trellis has reached its basic form, and to compute all ${\it \Gamma}_i(S_{\mu})$ the minimum between two sums must be determined in each case: |
::<math>{\it \Gamma}_i(S_0) ={\rm Min} \left [{\it \Gamma}_{i-1}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_2) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm},</math> | ::<math>{\it \Gamma}_i(S_0) ={\rm Min} \left [{\it \Gamma}_{i-1}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_2) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm},</math> | ||
| Line 70: | Line 70: | ||
::<math>{\it \Gamma}_i(S_3) ={\rm Min} \left [{\it \Gamma}_{i-1}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_3) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm}.</math> | ::<math>{\it \Gamma}_i(S_3) ={\rm Min} \left [{\it \Gamma}_{i-1}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_3) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm}.</math> | ||
| − | * | + | *Of the two branches arriving at a node ${\it \Gamma}_i(S_{\mu})$ the worse one (which would have led to a larger ${\it \Gamma}_i(S_{\mu})$ ) is eliminated. Only one branch then leads to each node.<br> |
| − | * | + | *Once all error values up to and including $i = 7$ have been determined, the viterbi algotithm can be completed by searching the connected path from the end of the trellis ⇒ ${\it \Gamma}_7(S_0)$ to the beginning ⇒ ${\it \Gamma}_0(S_0)$ . |
| + | <br> | ||
| − | * | + | *Through this path, the most likely code sequence $\underline{z}$ and the most likely information sequence $\underline{v}$ are then fixed. |
| − | * | + | *Not all receive sequences $\underline{y}$ are true, however $\underline{z} = \underline{x}$ and $\underline{v} = \underline{u}$. That is, '''If there are too many transmission errors, the Viterbi algorithm also fails'''.<br> |
| − | == | + | == Creating the trellis in the error-free case – error value calculation.== |
<br> | <br> | ||
| − | + | First, we assume the receive sequence $\underline{y} = (11, 01, 01, 11, 11, 10, 11)$ which here – is already divided into bit pairs $\underline{y}_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ \underline{y}_7$ is subdivided. The numerical values entered in the trellis and the different types of strokes are explained in the following text.<br> | |
| − | [[File:KC_T_3_4_S3a_neu.png|right|frame| | + | [[File:KC_T_3_4_S3a_neu.png|right|frame|Viterbi scheme for the received vector $\underline{y} = (11, 01, 01, 11, 11, 10, 11)$|class=fit]] |
| − | * | + | *Starting from the initial value ${\it \Gamma}_0(S_0) = 0$ we get $\underline{y}_1 = (11)$ by adding the Hamming distances |
| − | :$$d_{\rm H}((00), \ \underline{y}_1) = 2\text{ | + | :$$d_{\rm H}((00), \ \underline{y}_1) = 2\text{ or }d_{\rm H}((11), \ \underline{y}_1) = 0$$ |
| − | : | + | :to the error values ${\it \Gamma}_1(S_0) = 2, \ {\it \Gamma}_1(S_1) = 0$.<br> |
| − | * | + | *In the second decoding step there are error values for all four states: With $\underline{y}_2 = (01)$ one obtains: |
::<math>{\it \Gamma}_2(S_0) = {\it \Gamma}_1(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 2+1 = 3 \hspace{0.05cm},</math> | ::<math>{\it \Gamma}_2(S_0) = {\it \Gamma}_1(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 2+1 = 3 \hspace{0.05cm},</math> | ||
| Line 95: | Line 96: | ||
::<math>{\it \Gamma}_2(S_3) = {\it \Gamma}_1(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 0+0=0 \hspace{0.05cm}.</math> | ::<math>{\it \Gamma}_2(S_3) = {\it \Gamma}_1(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 0+0=0 \hspace{0.05cm}.</math> | ||
| − | *In | + | *In all further decoding steps, two values must be compared in each case, whereby the node ${\it \Gamma}_i(S_{\mu})$ is always assigned the smaller value. For example, for $i = 3$ with $\underline{y}_3 = (01)$: |
::<math>{\it \Gamma}_3(S_0) ={\rm min} \left [{\it \Gamma}_{2}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{2}(S_2) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] ={\rm min} \big [ 3+1\hspace{0.05cm},\hspace{0.05cm} 2+1 \big ] = 3\hspace{0.05cm},</math> | ::<math>{\it \Gamma}_3(S_0) ={\rm min} \left [{\it \Gamma}_{2}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{2}(S_2) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] ={\rm min} \big [ 3+1\hspace{0.05cm},\hspace{0.05cm} 2+1 \big ] = 3\hspace{0.05cm},</math> | ||
::<math>{\it \Gamma}_3(S_3) ={\rm min} \left [{\it \Gamma}_{2}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{2}(S_3) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] ={\rm min} \big [ 3+0\hspace{0.05cm},\hspace{0.05cm} 0+2 \big ] = 2\hspace{0.05cm}.</math> | ::<math>{\it \Gamma}_3(S_3) ={\rm min} \left [{\it \Gamma}_{2}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{2}(S_3) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] ={\rm min} \big [ 3+0\hspace{0.05cm},\hspace{0.05cm} 0+2 \big ] = 2\hspace{0.05cm}.</math> | ||
| − | * | + | *From $i = 6$ the termination of the convolutional code becomes effective in the considered example. Here only two comparisons are left to determine ${\it \Gamma}_6(S_0) = 3$ and ${\it \Gamma}_6(S_2)= 0$ and for $i = 7$ only one comparison with the final result ${\it \Gamma}_7(S_0) = 0$.<br> |
| − | + | The description of the Viterbi decoding process continues on the next page. | |
| − | == | + | == Evaluating the trellis in the error-free case – Path search.== |
<br> | <br> | ||
| − | + | After all error values ${\it \Gamma}_i(S_{\mu})$ – have been determined for $1 ≤ i ≤ 7$ and $0 ≤ \mu ≤ 3$ – in the present example, the Viterbi decoder can start the path search:<br> | |
| − | [[File:P ID2654 KC T 3 4 S3b v1.png|right|frame| | + | [[File:P ID2654 KC T 3 4 S3b v1.png|right|frame|Viterbi path search for for the received vector $\underline{y} = (11, 01, 01, 11, 11, 10, 11)$|class=fit]] |
| − | * | + | *The graphic shows the trellis after the error value calculation. All circles are assigned numerical values. |
| − | * | + | *However, the most probable path already drawn in the graphic is not yet known. |
| − | * | + | *Of the two branches arriving at a node, only the one that led to the minimum error value ${\it \Gamma}_i(S_{\mu})$ is used for the final path search. |
| − | * | + | *The "bad" branches are discarded. They are each shown dotted in the above graph. |
<br clear=all> | <br clear=all> | ||
| − | + | The path search runs as follows: | |
| − | * | + | *Starting from the end value ${\it \Gamma}_7(S_0)$ a continuous path is searched in backward direction to the start value ${\it \Gamma}_0(S_0)$ . Only the solid branches are allowed. Dotted lines cannot be part of the selected path.<br> |
| − | * | + | *The selected path traverses from right to left the states $S_0 ← S_2 ← S_1 ← S_0 ← S_2 ← S_3 ← S_1 ← S_0$ and is grayed out in the graph. There is no second continuous path from ${\it \Gamma}_7(S_0)$ to ${\it \Gamma}_0(S_0)$. This means: The decoding result is unique.<br> |
| − | * | + | *The result $\underline{v} = (1, 1, 0, 0, 1, 0, 0)$ of the Viterbi decoder with respect to the information sequence is obtained if for the continuous path – but now in forward direction from left to right – the colors of the individual branches are evaluated $($red corresponds to a $0$ and blue to a $1)$.<br><br> |
| − | + | From the final value ${\it \Gamma}_7(S_0) = 0$ it can be seen that there were no transmission errors in this first example: | |
| − | * | + | *The decoding result $\underline{z}$ thus matches the received vector $\underline{y} = (11, 01, 01, 11, 11, 10, 11)$ and the actual code sequence $\underline{x}$ . |
| − | * | + | *With error-free transmission, $\underline{v}$ is not only the most probable information sequence according to the ML criterion $\underline{u}$, but both are even identical: $\underline{v} \equiv \underline{u}$.<br> |
| − | <i> | + | <i>Note:</i> In the decoding described, of course, no use was made of the "error-free case" information already contained in the heading. |
| − | + | Now follow three examples of Viterbi decoding for the errorneous case. <br> | |
| − | == | + | == Decoding examples for the erroneous case == |
<br> | <br> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ We assume here the received vector $\underline{y} = \big (11\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11 \hspace{0.05cm} \hspace{0.05cm} \big ) $ which does not represent a valid code sequence $\underline{x}$ . The calculation of error sizes ${\it \Gamma}_i(S_{\mu})$ and the path search is done as described on page [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#Definition_of_the_free_distance| "Preliminaries"]] and demonstrated on the last two pages for the error-free case.<br> |
| − | [[File:P ID2655 KC T 3 4 S4a v1.png|center|frame| | + | [[File:P ID2655 KC T 3 4 S4a v1.png|center|frame|Decoding example with two bit errors|class=fit]] |
| − | + | As '''summary''' of this first example, it should be noted: | |
| − | * | + | *Also with the above trellis, a unique path (with a dark gray background) can be traced, leading to the following results. <br>(recognizable by the labels or the colors of this path): |
::<math>\underline{z} = \big (00\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11 \hspace{0.05cm} \big ) \hspace{0.05cm},</math> | ::<math>\underline{z} = \big (00\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11 \hspace{0.05cm} \big ) \hspace{0.05cm},</math> | ||
::<math> \underline{\upsilon} =\big (0\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0 \hspace{0.05cm} \big ) \hspace{0.05cm}.</math> | ::<math> \underline{\upsilon} =\big (0\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0 \hspace{0.05cm} \big ) \hspace{0.05cm}.</math> | ||
| − | * | + | *Comparing the most likely transmitted code sequence $\underline{z}$ with the received vector $\underline{y}$ shows that there were two bit errors here (right at the beginning). But since the used convolutional code has the [[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#Definition_of_the_free_distance| "free distance"]] $d_{\rm F} = 5$, two errors do not yet lead to a wrong decoding result.<br> |
| − | * | + | *There are other paths such as the lighter highlighted path $(S_0 → S_1 → S_3 → S_3 → S_2 → S_0 → S_0)$ that initially appear to be promising. Only in the last decoding step $(i = 7)$ can this light gray path finally be discarded.<br> |
| − | * | + | *The example shows that a too early decision is often not purposeful. One can also see the expediency of termination: With final decision at $i = 5$ (end of information sequence), the sequences $(0, 1, 0, 1, 1)$ and $(1, 1, 1, 1, 0)$ would still have been considered equally likely.<br><br> |
| − | <i> | + | <i>Notes:</i> In the calculation of ${\it \Gamma}_5(S_0) = 3$ and ${\it \Gamma}_5(S_1) = 3$ here in each case the two comparison branches lead to exactly the same minimum error value. In the graph these two special cases are marked by dash dots.<br> |
| − | *In | + | *In this example, this special case has no effect on the path search. |
| − | * | + | *Nevertheless, the algorithm always expects a decision between two competing branches. |
| − | *In | + | *In practice, one helps oneself by randomly selecting one of the two paths if they are equal.}}<br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ |
| − | + | In this example, we assume the following assumptions regarding source and encoder: | |
::<math>\underline{u} = \big (1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0\hspace{0.05cm}, 1 \hspace{0.05cm}, 0\hspace{0.05cm}, 0 \big )\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ::<math>\underline{u} = \big (1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0\hspace{0.05cm}, 1 \hspace{0.05cm}, 0\hspace{0.05cm}, 0 \big )\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
\underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 11 \hspace{0.05cm} \hspace{0.05cm} \big ) \hspace{0.05cm}.</math> | \underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 11 \hspace{0.05cm} \hspace{0.05cm} \big ) \hspace{0.05cm}.</math> | ||
| − | [[File:P ID2700 KC T 3 4 S4b v1.png|center|frame| | + | [[File:P ID2700 KC T 3 4 S4b v1.png|center|frame|Decoding example with three bit errors|class=fit]]<br> |
| − | + | From the graphic you can see that here the decoder decides for the correct path (dark background) despite three bit errors. | |
| − | * | + | *So there is not always a wrong decision, if more than $d_{\rm F}/2$ bit errors occurred. |
| − | * | + | *But with statistical distribution of the three transmission errors, wrong decision would be more frequent than right.}}<br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ Here also applies <math>\underline{u} = \big (1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0\hspace{0.05cm}, 1 \hspace{0.05cm}, 0\hspace{0.05cm}, 0 \big )\hspace{0.3cm}\Rightarrow \hspace{0.3cm} |
| − | \underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 11 \hspace{0.05cm} \hspace{0.05cm} \big ) \hspace{0.05cm}.</math> | + | \underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 11 \hspace{0.05cm} \hspace{0.05cm} \big ) \hspace{0.05cm}.</math> Unlike $\text{example 2}$ however, a fourth bit error is added in the form of $\underline{y}_7 = (01)$. |
| − | [[File:P ID2704 KC T 3 4 S4c v1.png|center|frame| | + | [[File:P ID2704 KC T 3 4 S4c v1.png|center|frame|Decoding example with four bit errors|class=fit]] |
| − | * | + | *Now both branches in step $i = 7$ lead to the minimum error value ${\it \Gamma}_7(S_0) = 4$, recognizable by the dash-dotted transitions. If one decides in the then required lottery procedure for the path with dark background, the correct decision is still made even with four bit errors: $\underline{v} = \big (1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0\hspace{0.05cm}, 1 \hspace{0.05cm}, 0\hspace{0.05cm}, 0 \big )$. <br> |
| − | * | + | *Otherwise, a wrong decision is made. Depending on the outcome of the dice roll in step $i =6$ between the two dash-dotted competitors, you choose either the purple or the light gray path. Both have little in common with the correct path.}} |
| − | == | + | == Relationship between Hamming distance and correlation == |
<br> | <br> | ||
| − | + | Especially for the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80. 93_BSC|"BSC Model"]] – but also for any other binary channel ⇒ input $x_i ∈ \{0,1\}$, output $y_i ∈ \{0,1\}$ such as the [[Digital_Signal_Transmission/Burst_Error_Channels#Channel_model_according_to_Gilbert-Elliott|"Gilbert–Elliott model"]] – provides the Hamming distance $d_{\rm H}(\underline{x}, \ \underline{y})$ exactly the same information about the similarity of the input sequence $\underline{x}$ and the output sequence $\underline{y}$ as the [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces#Nomenclature_in_the_fourth_chapter| "inner product"]]. Assuming that the two sequences are in bipolar representation (denoted by tildes) and that the sequence length is $L$ in each case, the inner product is: | |
::<math><\hspace{-0.1cm}\underline{\tilde{x}}, \hspace{0.05cm}\underline{\tilde{y}} \hspace{-0.1cm}> \hspace{0.15cm} | ::<math><\hspace{-0.1cm}\underline{\tilde{x}}, \hspace{0.05cm}\underline{\tilde{y}} \hspace{-0.1cm}> \hspace{0.15cm} | ||
= \sum_{i = 1}^{L} \tilde{x}_i \cdot \tilde{y}_i \hspace{0.3cm}{\rm mit } \hspace{0.2cm} \tilde{x}_i = 1 - 2 \cdot x_i \hspace{0.05cm},\hspace{0.2cm} \tilde{y}_i = 1 - 2 \cdot y_i \hspace{0.05cm},\hspace{0.2cm} \tilde{x}_i, \hspace{0.05cm}\tilde{y}_i \in \hspace{0.1cm}\{ -1, +1\} \hspace{0.05cm}.</math> | = \sum_{i = 1}^{L} \tilde{x}_i \cdot \tilde{y}_i \hspace{0.3cm}{\rm mit } \hspace{0.2cm} \tilde{x}_i = 1 - 2 \cdot x_i \hspace{0.05cm},\hspace{0.2cm} \tilde{y}_i = 1 - 2 \cdot y_i \hspace{0.05cm},\hspace{0.2cm} \tilde{x}_i, \hspace{0.05cm}\tilde{y}_i \in \hspace{0.1cm}\{ -1, +1\} \hspace{0.05cm}.</math> | ||
| − | + | We sometimes refer to this inner product as the "correlation value". The quotation marks are to indicate that the range of values of a [[Theory_of_Stochastic_Signals/Two-Dimensional_Random_Variables#Correlation_coefficient| "correlation coefficient"]] is actually $±1$.<br> | |
| − | [[File:KC_T_3_4_S5_neu.png|right|frame| | + | [[File:KC_T_3_4_S5_neu.png|right|frame|Relationship between Haming distance and "correlation value" |class=fit]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 4:}$ Wir betrachten hier zwei Binärfolgen der Länge $L = 10$.<br> | $\text{Beispiel 4:}$ Wir betrachten hier zwei Binärfolgen der Länge $L = 10$.<br> | ||
| − | * | + | *Shown on the left are the unipolar sequences $\underline{x}$ and $\underline{y}$ and the product $\underline{x} \cdot \underline{y}$. |
| − | * | + | *You can see the Hamming distance $d_{\rm H}(\underline{x}, \ \underline{y}) = 6$ ⇒ six bit errors at the arrow positions. |
| − | * | + | *The inner product $ < \underline{x} \cdot \underline{y} > \hspace{0.15cm} = \hspace{0.15cm}0$ has no significance here. For example, $< \underline{0} \cdot \underline{y} > $ is always zero regardless of $\underline{y}$ . |
| − | + | The Hamming distance $d_{\rm H} = 6$ can also be seen from the bipolar (antipodal) plot of the right graph. | |
| − | * | + | *The "correlation value" now has the correct value: |
:$$4 \cdot (+1) + 6 \cdot (-1) = \, -2.$$ | :$$4 \cdot (+1) + 6 \cdot (-1) = \, -2.$$ | ||
| − | * | + | *The deterministic relation between the two quantities with the sequence length $L$ holds: |
:$$ < \underline{ \tilde{x} } \cdot \underline{\tilde{y} } > \hspace{0.15cm} = \hspace{0.15cm} L - 2 \cdot d_{\rm H} (\underline{\tilde{x} }, \hspace{0.05cm}\underline{\tilde{y} })\hspace{0.05cm}. $$}} | :$$ < \underline{ \tilde{x} } \cdot \underline{\tilde{y} } > \hspace{0.15cm} = \hspace{0.15cm} L - 2 \cdot d_{\rm H} (\underline{\tilde{x} }, \hspace{0.05cm}\underline{\tilde{y} })\hspace{0.05cm}. $$}} | ||
| Line 207: | Line 208: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ Let us now interpret this equation for some special cases: |
| − | * | + | *Identical sequences: The Hamming distance is equal $0$ and the "correlation value" is equal $L$.<br> |
| − | * | + | *Inverted: Consequences: The Hamming distance is equal to $L$ and the "correlation value" is equal to $-L$.<br> |
| − | * | + | *Uncorrelated sequences: The Hamming distance is equal to $L/2$, the "correlation value" is equal to $0$.}} |
== Viterbi algorithm based on correlation and metrics == | == Viterbi algorithm based on correlation and metrics == | ||
<br> | <br> | ||
| − | + | Using the insights of the last page, the Viterbi algorithm can also be characterized as follows. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Alternative | + | $\text{Alternative description:}$ |
| − | + | The Viterbi algorithm searches from all possible code sequences $\underline{x}' ∈ \mathcal{C}$ the sequence $\underline{z}$ with the maximum " correlation value" to the receiving sequence $\underline{y}$: | |
::<math>\underline{z} = {\rm arg} \max_{\underline{x}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} \left\langle \tilde{\underline{x} }'\hspace{0.05cm} ,\hspace{0.05cm} \tilde{\underline{y} } \right\rangle | ::<math>\underline{z} = {\rm arg} \max_{\underline{x}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} \left\langle \tilde{\underline{x} }'\hspace{0.05cm} ,\hspace{0.05cm} \tilde{\underline{y} } \right\rangle | ||
| Line 227: | Line 228: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | $〈\ \text{ ...} \ 〉$ | + | $〈\ \text{ ...} \ 〉$ denotes a "correlation value" according to the statements on the last page. The tildes again indicate the bipolar (antipodal) representation.}}<br> |
Die Grafik zeigt die diesbezügliche Trellisauswertung. Zugrunde liegt wie für die [[Channel_Coding/Decodierung_von_Faltungscodes#Decodierbeispiele_f.C3.BCr_den_fehlerbehafteten_Fall| Trellisauswertung gemäß Beispiel 1]] – basierend auf der minimalen Hamming–Distanz und den Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ – wieder die Eingangsfolge | Die Grafik zeigt die diesbezügliche Trellisauswertung. Zugrunde liegt wie für die [[Channel_Coding/Decodierung_von_Faltungscodes#Decodierbeispiele_f.C3.BCr_den_fehlerbehafteten_Fall| Trellisauswertung gemäß Beispiel 1]] – basierend auf der minimalen Hamming–Distanz und den Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ – wieder die Eingangsfolge | ||
Revision as of 20:32, 9 October 2022
Contents
- 1 Block diagram and requirements
- 2 Preliminary remarks on the following decoding examples
- 3 Creating the trellis in the error-free case – error value calculation.
- 4 Evaluating the trellis in the error-free case – Path search.
- 5 Decoding examples for the erroneous case
- 6 Relationship between Hamming distance and correlation
- 7 Viterbi algorithm based on correlation and metrics
- 8 Viterbi–Entscheidung bei nicht–terminierten Faltungscodes
- 9 Weitere Decodierverfahren für Faltungscodes
- 10 Aufgaben zum Kapitel
- 11 Quellenverzeichnis
Block diagram and requirements
A significant advantage of convolutional coding is that there is a very efficient decoding method for this in the form of the Viterbi algorithm. This algorithm, developed by "Andrew James Viterbi" has already been described in the chapter "Viterbi receiver" of the book "Digital Signal Transmission" with regard to its use for equalization.
For its use as a convolutional decoder we assume the above block diagram and the following prerequisites:
- The information sequence $\underline{u} = (u_1, \ u_2, \ \text{... } \ )$ is here in contrast to the description of linear block codes ⇒ "first main chapter" or of Reed– Solomon–Codes ⇒ "second main chapter" generally infinitely long ("semi–infinite" ). For the information symbols always applies $u_i ∈ \{0, 1\}$.
- The code sequence $\underline{x} = (x_1, \ x_2, \ \text{... })$ with $x_i ∈ \{0, 1\}$ depends not only on $\underline{u}$ but also on the code rate $R = 1/n$, the memory $m$ and the transfer function matrix $\mathbf{G}(D)$ . For finite number $L$ of information bits, the convolutional code should be terminated by appending $m$ zeros:
- \[\underline{u}= (u_1,\hspace{0.05cm} u_2,\hspace{0.05cm} \text{...} \hspace{0.1cm}, u_L, \hspace{0.05cm} 0 \hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.1cm}, 0 ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{x}= (x_1,\hspace{0.05cm} x_2,\hspace{0.05cm} \text{...} \hspace{0.1cm}, x_{2L}, \hspace{0.05cm} x_{2L+1} ,\hspace{0.05cm} \text{...} \hspace{0.1cm}, \hspace{0.05cm} x_{2L+2m} ) \hspace{0.05cm}.\]
- The received sequence $\underline{y} = (y_1, \ y_2, \ \text{...} )$ results according to the assumed channel model. For a digital model like the "Binary Symmetric Channel" (BSC) holds $y_i ∈ \{0, 1\}$, so the corruption of $\underline{x}$ to $\underline{y}$ with the "Hamming distance" $d_{\rm H}(\underline{x}, \underline{y})$ can be quantified. The required modifications for the "AWGN channel" follow in the section "Viterbi algorithm based on correlation and metrics".
- The Viterbi algorithm provides an estimate $\underline{z}$ for the code sequence $\underline{x}$ and another estimate $\underline{v}$ for the information sequence $\underline{u}$. Thereby holds:
- \[{\rm Pr}(\underline{z} \ne \underline{x})\stackrel{!}{=}{\rm Minimum} \hspace{0.25cm}\Rightarrow \hspace{0.25cm} {\rm Pr}(\underline{\upsilon} \ne \underline{u})\stackrel{!}{=}{\rm Minimum} \hspace{0.05cm}.\]
$\text{Conclusion:}$ Given a digital channel model (for example, the BSC model), the Viterbi algorithm searches from all possible code sequences $\underline{x}\hspace{0.05cm}'$ the sequence $\underline{z}$ with the minimum Hamming distance $d_{\rm H}(\underline{x}\hspace{0.05cm}', \underline{y})$ to the receiving sequence $\underline{y}$:
\[\underline{z} = {\rm arg} \min_{\underline{x}\hspace{0.05cm}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} d_{\rm H}( \underline{x}\hspace{0.05cm}'\hspace{0.02cm},\hspace{0.02cm} \underline{y} ) = {\rm arg} \max_{\underline{x}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} {\rm Pr}( \underline{y} \hspace{0.05cm} \vert \hspace{0.05cm} \underline{x}')\hspace{0.05cm}.\]
This also means: The Viterbi algorithm satisfies the "maximum likelihood criterion".
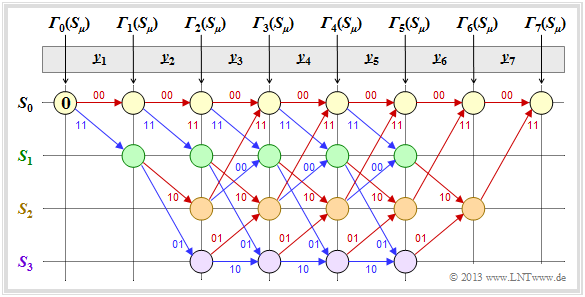
Preliminary remarks on the following decoding examples
The following prerequisites apply to all examples in this chapter:
- Standard convolutional encoder: Rate $R = 1/2$, Memory $m = 2$;
- transfer function matrix: $\mathbf{G}(D) = (1 + D + D^2, 1 + D^2)$;
- Length of information sequence: $L = 5$;
- Consideration of termination: $L\hspace{0.05cm}' = 7$;
- Length of sequences $\underline{x}$ and $\underline{y}$ : $14$ bits each;
- Distribution according to $\underline{y} = (\underline{y}_1, \ \underline{y}_2, \ \text{...} \ , \ \underline{y}_7)$
⇒ bit pairs $\underline{y}_i ∈ \{00, 01, 10, 11\}$; - Viterbi decoding using trellis diagram:
- red arrow ⇒ hypothesis $u_i = 0$,
- blue arrow ⇒ hypothesis $u_i = 1$;
- hypothetical code sequence $\underline{x}_i\hspace{0.01cm}' ∈ \{00, 01, 10, 11\}$;
- all hypothetical quantities with apostrophe.
We always assume that the Viterbi decoding is done at the Hamming distance $d_{\rm H}(\underline{x}_i\hspace{0. 01cm}', \ \underline{y}_i)$ between the received word $\underline{y}_i$ and the four possible codewords $x_i\hspace{0.01cm}' ∈ \{00, 01, 10, 11\}$ is based. We then proceed as follows:
- In the still empty circles the error value ${\it \Gamma}_i(S_{\mu})$ of the states $S_{\mu} (0 ≤ \mu ≤ 3)$ at the time points $i$ are entered. The initial value is always ${\it \Gamma}_0(S_0) = 0$.
- The error values for $i = 1$ and $i = 2$ are given by
- \[{\it \Gamma}_1(S_0) =d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_1 \big ) \hspace{0.05cm}, \hspace{2.38cm}{\it \Gamma}_1(S_1) = d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_1 \big ) \hspace{0.05cm},\]
- \[{\it \Gamma}_2(S_0) ={\it \Gamma}_1(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big )\hspace{0.05cm}, \hspace{0.6cm}{\it \Gamma}_2(S_1) = {\it \Gamma}_1(S_0)+ d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big ) \hspace{0.05cm},\hspace{0.6cm}{\it \Gamma}_2(S_2) ={\it \Gamma}_1(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big )\hspace{0.05cm}, \hspace{0.6cm}{\it \Gamma}_2(S_3) = {\it \Gamma}_1(S_1)+ d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_2 \big ) \hspace{0.05cm}.\]
- From $i = 3$ the trellis has reached its basic form, and to compute all ${\it \Gamma}_i(S_{\mu})$ the minimum between two sums must be determined in each case:
- \[{\it \Gamma}_i(S_0) ={\rm Min} \left [{\it \Gamma}_{i-1}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_2) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm},\]
- \[{\it \Gamma}_i(S_1)={\rm Min} \left [{\it \Gamma}_{i-1}(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_2) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm},\]
- \[{\it \Gamma}_i(S_2) ={\rm Min} \left [{\it \Gamma}_{i-1}(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_3) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm},\]
- \[{\it \Gamma}_i(S_3) ={\rm Min} \left [{\it \Gamma}_{i-1}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{i-1}(S_3) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} \underline{y}_i \big ) \right ] \hspace{0.05cm}.\]
- Of the two branches arriving at a node ${\it \Gamma}_i(S_{\mu})$ the worse one (which would have led to a larger ${\it \Gamma}_i(S_{\mu})$ ) is eliminated. Only one branch then leads to each node.
- Once all error values up to and including $i = 7$ have been determined, the viterbi algotithm can be completed by searching the connected path from the end of the trellis ⇒ ${\it \Gamma}_7(S_0)$ to the beginning ⇒ ${\it \Gamma}_0(S_0)$ .
- Through this path, the most likely code sequence $\underline{z}$ and the most likely information sequence $\underline{v}$ are then fixed.
- Not all receive sequences $\underline{y}$ are true, however $\underline{z} = \underline{x}$ and $\underline{v} = \underline{u}$. That is, If there are too many transmission errors, the Viterbi algorithm also fails.
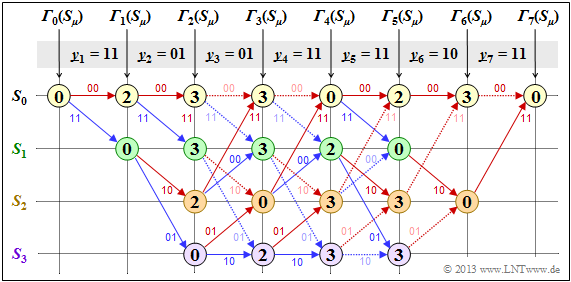
Creating the trellis in the error-free case – error value calculation.
First, we assume the receive sequence $\underline{y} = (11, 01, 01, 11, 11, 10, 11)$ which here – is already divided into bit pairs $\underline{y}_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ \underline{y}_7$ is subdivided. The numerical values entered in the trellis and the different types of strokes are explained in the following text.
- Starting from the initial value ${\it \Gamma}_0(S_0) = 0$ we get $\underline{y}_1 = (11)$ by adding the Hamming distances
- $$d_{\rm H}((00), \ \underline{y}_1) = 2\text{ or }d_{\rm H}((11), \ \underline{y}_1) = 0$$
- to the error values ${\it \Gamma}_1(S_0) = 2, \ {\it \Gamma}_1(S_1) = 0$.
- In the second decoding step there are error values for all four states: With $\underline{y}_2 = (01)$ one obtains:
- \[{\it \Gamma}_2(S_0) = {\it \Gamma}_1(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 2+1 = 3 \hspace{0.05cm},\]
- \[{\it \Gamma}_2(S_1) ={\it \Gamma}_1(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 2+1 = 3 \hspace{0.05cm},\]
- \[{\it \Gamma}_2(S_2) ={\it \Gamma}_1(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 0+2=2 \hspace{0.05cm},\]
- \[{\it \Gamma}_2(S_3) = {\it \Gamma}_1(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) = 0+0=0 \hspace{0.05cm}.\]
- In all further decoding steps, two values must be compared in each case, whereby the node ${\it \Gamma}_i(S_{\mu})$ is always assigned the smaller value. For example, for $i = 3$ with $\underline{y}_3 = (01)$:
- \[{\it \Gamma}_3(S_0) ={\rm min} \left [{\it \Gamma}_{2}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{2}(S_2) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] ={\rm min} \big [ 3+1\hspace{0.05cm},\hspace{0.05cm} 2+1 \big ] = 3\hspace{0.05cm},\]
- \[{\it \Gamma}_3(S_3) ={\rm min} \left [{\it \Gamma}_{2}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{2}(S_3) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] ={\rm min} \big [ 3+0\hspace{0.05cm},\hspace{0.05cm} 0+2 \big ] = 2\hspace{0.05cm}.\]
- From $i = 6$ the termination of the convolutional code becomes effective in the considered example. Here only two comparisons are left to determine ${\it \Gamma}_6(S_0) = 3$ and ${\it \Gamma}_6(S_2)= 0$ and for $i = 7$ only one comparison with the final result ${\it \Gamma}_7(S_0) = 0$.
The description of the Viterbi decoding process continues on the next page.
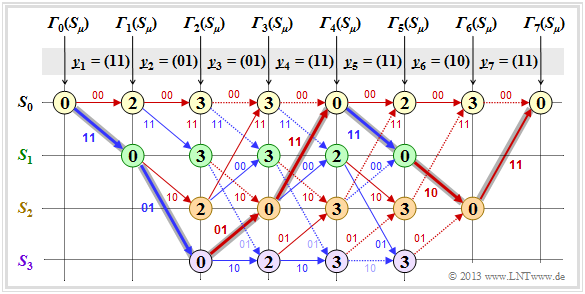
Evaluating the trellis in the error-free case – Path search.
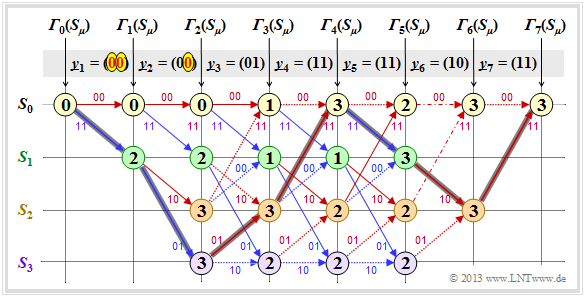
After all error values ${\it \Gamma}_i(S_{\mu})$ – have been determined for $1 ≤ i ≤ 7$ and $0 ≤ \mu ≤ 3$ – in the present example, the Viterbi decoder can start the path search:
- The graphic shows the trellis after the error value calculation. All circles are assigned numerical values.
- However, the most probable path already drawn in the graphic is not yet known.
- Of the two branches arriving at a node, only the one that led to the minimum error value ${\it \Gamma}_i(S_{\mu})$ is used for the final path search.
- The "bad" branches are discarded. They are each shown dotted in the above graph.
The path search runs as follows:
- Starting from the end value ${\it \Gamma}_7(S_0)$ a continuous path is searched in backward direction to the start value ${\it \Gamma}_0(S_0)$ . Only the solid branches are allowed. Dotted lines cannot be part of the selected path.
- The selected path traverses from right to left the states $S_0 ← S_2 ← S_1 ← S_0 ← S_2 ← S_3 ← S_1 ← S_0$ and is grayed out in the graph. There is no second continuous path from ${\it \Gamma}_7(S_0)$ to ${\it \Gamma}_0(S_0)$. This means: The decoding result is unique.
- The result $\underline{v} = (1, 1, 0, 0, 1, 0, 0)$ of the Viterbi decoder with respect to the information sequence is obtained if for the continuous path – but now in forward direction from left to right – the colors of the individual branches are evaluated $($red corresponds to a $0$ and blue to a $1)$.
From the final value ${\it \Gamma}_7(S_0) = 0$ it can be seen that there were no transmission errors in this first example:
- The decoding result $\underline{z}$ thus matches the received vector $\underline{y} = (11, 01, 01, 11, 11, 10, 11)$ and the actual code sequence $\underline{x}$ .
- With error-free transmission, $\underline{v}$ is not only the most probable information sequence according to the ML criterion $\underline{u}$, but both are even identical: $\underline{v} \equiv \underline{u}$.
Note: In the decoding described, of course, no use was made of the "error-free case" information already contained in the heading.
Now follow three examples of Viterbi decoding for the errorneous case.
Decoding examples for the erroneous case
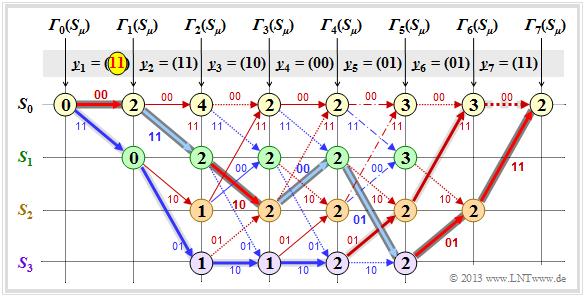
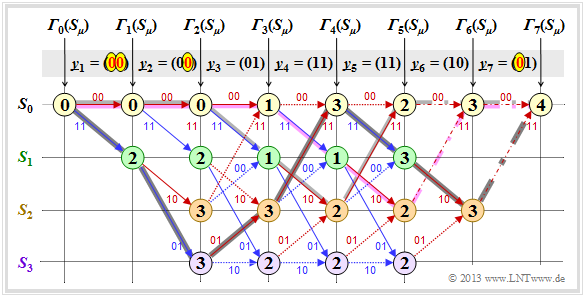
$\text{Example 1:}$ We assume here the received vector $\underline{y} = \big (11\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11 \hspace{0.05cm} \hspace{0.05cm} \big ) $ which does not represent a valid code sequence $\underline{x}$ . The calculation of error sizes ${\it \Gamma}_i(S_{\mu})$ and the path search is done as described on page "Preliminaries" and demonstrated on the last two pages for the error-free case.
As summary of this first example, it should be noted:
- Also with the above trellis, a unique path (with a dark gray background) can be traced, leading to the following results.
(recognizable by the labels or the colors of this path):
- \[\underline{z} = \big (00\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 00\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11 \hspace{0.05cm} \big ) \hspace{0.05cm},\]
- \[ \underline{\upsilon} =\big (0\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0 \hspace{0.05cm} \big ) \hspace{0.05cm}.\]
- Comparing the most likely transmitted code sequence $\underline{z}$ with the received vector $\underline{y}$ shows that there were two bit errors here (right at the beginning). But since the used convolutional code has the "free distance" $d_{\rm F} = 5$, two errors do not yet lead to a wrong decoding result.
- There are other paths such as the lighter highlighted path $(S_0 → S_1 → S_3 → S_3 → S_2 → S_0 → S_0)$ that initially appear to be promising. Only in the last decoding step $(i = 7)$ can this light gray path finally be discarded.
- The example shows that a too early decision is often not purposeful. One can also see the expediency of termination: With final decision at $i = 5$ (end of information sequence), the sequences $(0, 1, 0, 1, 1)$ and $(1, 1, 1, 1, 0)$ would still have been considered equally likely.
Notes: In the calculation of ${\it \Gamma}_5(S_0) = 3$ and ${\it \Gamma}_5(S_1) = 3$ here in each case the two comparison branches lead to exactly the same minimum error value. In the graph these two special cases are marked by dash dots.
- In this example, this special case has no effect on the path search.
- Nevertheless, the algorithm always expects a decision between two competing branches.
- In practice, one helps oneself by randomly selecting one of the two paths if they are equal.
$\text{Example 2:}$ In this example, we assume the following assumptions regarding source and encoder:
- \[\underline{u} = \big (1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0\hspace{0.05cm}, 1 \hspace{0.05cm}, 0\hspace{0.05cm}, 0 \big )\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 11 \hspace{0.05cm} \hspace{0.05cm} \big ) \hspace{0.05cm}.\]
From the graphic you can see that here the decoder decides for the correct path (dark background) despite three bit errors.
- So there is not always a wrong decision, if more than $d_{\rm F}/2$ bit errors occurred.
- But with statistical distribution of the three transmission errors, wrong decision would be more frequent than right.
$\text{Example 3:}$ Here also applies \(\underline{u} = \big (1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0\hspace{0.05cm}, 1 \hspace{0.05cm}, 0\hspace{0.05cm}, 0 \big )\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 01\hspace{0.05cm}, 11\hspace{0.05cm}, 11\hspace{0.05cm}, 10\hspace{0.05cm}, 11 \hspace{0.05cm} \hspace{0.05cm} \big ) \hspace{0.05cm}.\) Unlike $\text{example 2}$ however, a fourth bit error is added in the form of $\underline{y}_7 = (01)$.
- Now both branches in step $i = 7$ lead to the minimum error value ${\it \Gamma}_7(S_0) = 4$, recognizable by the dash-dotted transitions. If one decides in the then required lottery procedure for the path with dark background, the correct decision is still made even with four bit errors: $\underline{v} = \big (1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0\hspace{0.05cm}, 1 \hspace{0.05cm}, 0\hspace{0.05cm}, 0 \big )$.
- Otherwise, a wrong decision is made. Depending on the outcome of the dice roll in step $i =6$ between the two dash-dotted competitors, you choose either the purple or the light gray path. Both have little in common with the correct path.
Relationship between Hamming distance and correlation
Especially for the "BSC Model" – but also for any other binary channel ⇒ input $x_i ∈ \{0,1\}$, output $y_i ∈ \{0,1\}$ such as the "Gilbert–Elliott model" – provides the Hamming distance $d_{\rm H}(\underline{x}, \ \underline{y})$ exactly the same information about the similarity of the input sequence $\underline{x}$ and the output sequence $\underline{y}$ as the "inner product". Assuming that the two sequences are in bipolar representation (denoted by tildes) and that the sequence length is $L$ in each case, the inner product is:
- \[<\hspace{-0.1cm}\underline{\tilde{x}}, \hspace{0.05cm}\underline{\tilde{y}} \hspace{-0.1cm}> \hspace{0.15cm} = \sum_{i = 1}^{L} \tilde{x}_i \cdot \tilde{y}_i \hspace{0.3cm}{\rm mit } \hspace{0.2cm} \tilde{x}_i = 1 - 2 \cdot x_i \hspace{0.05cm},\hspace{0.2cm} \tilde{y}_i = 1 - 2 \cdot y_i \hspace{0.05cm},\hspace{0.2cm} \tilde{x}_i, \hspace{0.05cm}\tilde{y}_i \in \hspace{0.1cm}\{ -1, +1\} \hspace{0.05cm}.\]
We sometimes refer to this inner product as the "correlation value". The quotation marks are to indicate that the range of values of a "correlation coefficient" is actually $±1$.
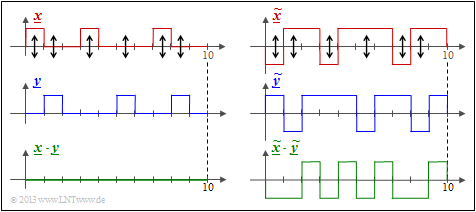
$\text{Beispiel 4:}$ Wir betrachten hier zwei Binärfolgen der Länge $L = 10$.
- Shown on the left are the unipolar sequences $\underline{x}$ and $\underline{y}$ and the product $\underline{x} \cdot \underline{y}$.
- You can see the Hamming distance $d_{\rm H}(\underline{x}, \ \underline{y}) = 6$ ⇒ six bit errors at the arrow positions.
- The inner product $ < \underline{x} \cdot \underline{y} > \hspace{0.15cm} = \hspace{0.15cm}0$ has no significance here. For example, $< \underline{0} \cdot \underline{y} > $ is always zero regardless of $\underline{y}$ .
The Hamming distance $d_{\rm H} = 6$ can also be seen from the bipolar (antipodal) plot of the right graph.
- The "correlation value" now has the correct value:
- $$4 \cdot (+1) + 6 \cdot (-1) = \, -2.$$
- The deterministic relation between the two quantities with the sequence length $L$ holds:
- $$ < \underline{ \tilde{x} } \cdot \underline{\tilde{y} } > \hspace{0.15cm} = \hspace{0.15cm} L - 2 \cdot d_{\rm H} (\underline{\tilde{x} }, \hspace{0.05cm}\underline{\tilde{y} })\hspace{0.05cm}. $$
$\text{Conclusion:}$ Let us now interpret this equation for some special cases:
- Identical sequences: The Hamming distance is equal $0$ and the "correlation value" is equal $L$.
- Inverted: Consequences: The Hamming distance is equal to $L$ and the "correlation value" is equal to $-L$.
- Uncorrelated sequences: The Hamming distance is equal to $L/2$, the "correlation value" is equal to $0$.
Viterbi algorithm based on correlation and metrics
Using the insights of the last page, the Viterbi algorithm can also be characterized as follows.
$\text{Alternative description:}$ The Viterbi algorithm searches from all possible code sequences $\underline{x}' ∈ \mathcal{C}$ the sequence $\underline{z}$ with the maximum " correlation value" to the receiving sequence $\underline{y}$:
- \[\underline{z} = {\rm arg} \max_{\underline{x}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm} \left\langle \tilde{\underline{x} }'\hspace{0.05cm} ,\hspace{0.05cm} \tilde{\underline{y} } \right\rangle \hspace{0.4cm}{\rm mit }\hspace{0.4cm}\tilde{\underline{x} }\hspace{0.05cm}'= 1 - 2 \cdot \underline{x}'\hspace{0.05cm}, \hspace{0.2cm} \tilde{\underline{y} }= 1 - 2 \cdot \underline{y} \hspace{0.05cm}.\]
$〈\ \text{ ...} \ 〉$ denotes a "correlation value" according to the statements on the last page. The tildes again indicate the bipolar (antipodal) representation.
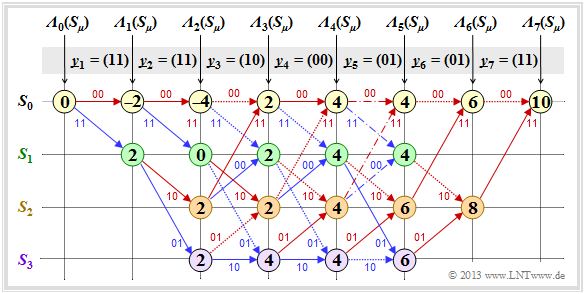
Die Grafik zeigt die diesbezügliche Trellisauswertung. Zugrunde liegt wie für die Trellisauswertung gemäß Beispiel 1 – basierend auf der minimalen Hamming–Distanz und den Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ – wieder die Eingangsfolge $\underline{u} = \big (0\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 1\hspace{0.05cm}, 1\hspace{0.05cm}, 0\hspace{0.05cm}, 0 \hspace{0.05cm} \big )$ ⇒ Codefolge $\underline{x} = \big (00, 11, 10, 00, 01, 01, 11 \big ) \hspace{0.05cm}.$
Weiter werden vorausgesetzt:
- der Standard–Faltungscodierer: Rate $R = 1/2$, Gedächtnis $m = 2$;
- die Übertragungsfunktionsmatrix: $\mathbf{G}(D) = (1 + D + D^2, 1 + D^2)$;
- Länge der Informationssequenz: $L = 5$;
- Berücksichtigung der Terminierung: $L' = 7$;
- der Empfangsvektor $\underline{y} = (11, 11, 10, 00, 01, 01, 11)$
⇒ zwei Bitfehler zu Beginn; - Viterbi–Decodierung mittels Trellisdiagramms:
- roter Pfeil ⇒ Hypothese $u_i = 0$,
- blauer Pfeil ⇒ Hypothese $u_i = 1$.
Nebenstehendes Trellis und die Trellisauswertung gemäß Beispiel 1 ähneln sich sehr. Ebenso wie die Suche nach der Sequenz mit der minimalen Hamming–Distanz geschieht auch die Suche nach dem maximalen Korrelationswert schrittweise:
- Die Knoten bezeichnet man hier als die Metriken ${\it \Lambda}_i(S_{\mu})$.
- Die englische Bezeichnung hierfür ist Cumulative Metric, während Branch Metric den Metrikzuwachs angibt.
- Der Endwert ${\it \Lambda}_7(S_0) = 10$ gibt den "Korrelationswert" zwischen der ausgewählten Folge $\underline{z}$ und dem Empfangsvektor $\underline{y}$ an.
- Im fehlerfreien Fall ergäbe sich ${\it \Lambda}_7(S_0) = 14$.
$\text{Beispiel 5:}$ Die folgende Detailbeschreibung der Trellisauswertung beziehen sich auf das obige Trellis:
- Die Metriken zum Zeitpunkt $i = 1$ ergeben sich mit $\underline{y}_1 = (11)$ zu
- \[{\it \Lambda}_1(S_0) \hspace{0.15cm} = \hspace{0.15cm} <\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.2cm}<(+1,\hspace{0.05cm} +1)\hspace{0.05cm}, \hspace{0.05cm}(-1,\hspace{0.05cm} -1) >\hspace{0.1cm} = \hspace{0.1cm} -2 \hspace{0.05cm},\]
- \[{\it \Lambda}_1(S_1) \hspace{0.15cm} = \hspace{0.15cm} <\hspace{-0.05cm}(11)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.2cm}<(-1,\hspace{0.05cm} -1)\hspace{0.05cm}, \hspace{0.05cm}(-1,\hspace{0.05cm} -1) >\hspace{0.1cm} = \hspace{0.1cm} +2 \hspace{0.05cm}.\]
- Entsprechend gilt zum Zeitpunkt $i = 2$ mit $\underline{y}_2 = (11)$:
- \[{\it \Lambda}_2(S_0) = {\it \Lambda}_1(S_0) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.1cm} -2-2 = -4 \hspace{0.05cm},\]
- \[{\it \Lambda}_2(S_1) = {\it \Lambda}_1(S_0) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(11)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.1cm} -2+2 = 0 \hspace{0.05cm},\]
- \[{\it \Lambda}_2(S_2)= {\it \Lambda}_1(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(10)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.1cm} +2+0 = +2 \hspace{0.05cm},\]
- \[{\it \Lambda}_2(S_3)= {\it \Lambda}_1(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(01)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} = \hspace{0.1cm} +2+0 = +2 \hspace{0.05cm}.\]
- Ab dem Zeitpunkt $i =3$ muss eine Entscheidung zwischen zwei Metriken getroffen werden. Beispielsweise erhält man mit $\underline{y}_3 = (10)$ für die oberste und die unterste Metrik im Trellis:
- \[{\it \Lambda}_3(S_0)={\rm max} \left [{\it \Lambda}_{2}(S_0) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}>\hspace{0.2cm} \hspace{0.05cm}, \hspace{0.2cm}{\it \Lambda}_{2}(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(00)\hspace{0.05cm}, \hspace{0.05cm}(11) \hspace{-0.05cm}> \right ] = {\rm max} \left [ -4+0\hspace{0.05cm},\hspace{0.05cm} +2+0 \right ] = +2\hspace{0.05cm},\]
- \[{\it \Lambda}_3(S_3) ={\rm max} \left [{\it \Lambda}_{2}(S_1) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(01)\hspace{0.05cm}, \hspace{0.05cm}(10) \hspace{-0.05cm}>\hspace{0.2cm} \hspace{0.05cm}, \hspace{0.2cm}{\it \Lambda}_{2}(S_3) \hspace{0.2cm}+ \hspace{0.1cm}<\hspace{-0.05cm}(10)\hspace{0.05cm}, \hspace{0.05cm}(10) \hspace{-0.05cm}> \right ] = {\rm max} \left [ 0+0\hspace{0.05cm},\hspace{0.05cm} +2+2 \right ] = +4\hspace{0.05cm}.\]
Vergleicht man die zu zu maximierenden Metriken ${\it \Lambda}_i(S_{\mu})$ mit den zu minimierenden Fehlergrößen ${\it \Gamma}_i(S_{\mu})$ gemäß dem $\text{Beispiel 1}$, so erkennt man den folgenden deterministischen Zusammenhang:
- \[{\it \Lambda}_i(S_{\mu}) = 2 \cdot \big [ i - {\it \Gamma}_i(S_{\mu}) \big ] \hspace{0.05cm}.\]
Die Auswahl der zu den einzelnen Decodierschritten überlebenden Zweige ist bei beiden Verfahren identisch, und auch die Pfadsuche liefert das gleiche Ergebnis.
$\text{Fazit:}$
- Beim Binärkanal – zum Beispiel nach dem BSC–Modell – führen die beiden beschriebenen Viterbi–Varianten "Fehlergrößenminimierung" und "Metrikmaximierung" zum gleichen Ergebnis.
- Beim AWGN–Kanal ist dagegen die Fehlergrößenminimierung nicht anwendbar, da keine Hamming–Distanz zwischen dem binären Eingang $\underline{x}$ und dem analogen Ausgang $\underline{y}$ angegeben werden kann.
- Die Metrikmaximierung ist beim AWGN–Kanal vielmehr identisch mit der Minimierung der Euklidischen Distanz – siehe Aufgabe 3.10Z.
- Ein weiterer Vorteil der Metrikmaximierung ist, dass eine Zuverlässigkeitsinformation über die Empfangswerte $\underline{y}$ in einfacher Weise berücksichtigt werden kann.
Viterbi–Entscheidung bei nicht–terminierten Faltungscodes
Bisher wurde stets ein terminierter Faltungscode der Länge $L\hspace{0.05cm}' = L + m$ betrachtet, und das Ergebnis des Viterbi–Decoders war der durchgehende Trellispfad vom Startzeitpunkt $(i = 0)$ bis zum Ende $(i = L\hspace{0.05cm}')$.
- Bei nicht–terminierten Faltungscodes $(L\hspace{0.05cm}' → ∞)$ ist diese Entscheidungsstrategie nicht anwendbar.
- Hier muss der Algorithmus abgewandelt werden, um in endlicher Zeit eine bestmögliche Schätzung (gemäß Maximum–Likelihood) der einlaufenden Bits der Codesequenz liefern zu können.
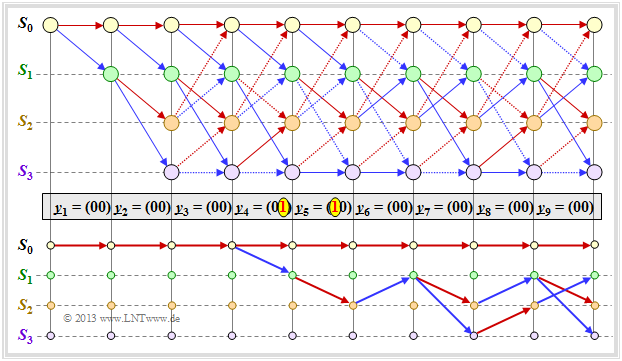
Die Grafik zeigt im oberen Teil ein beispielhaftes Trellis für
- "unseren" Standard–Codierer ⇒ $R = 1/2, \ m = 2, \ {\rm G}(D) = (1 + D + D^2, \ 1 + D^2)$,
- die Nullfolge ⇒ $\underline{u} = \underline{0} = (0, 0, 0, \ \text{...})$ ⇒ $\underline{x} = \underline{0} = (00, 00, 00, \ \text{...})$,
- jeweils einen Übertragungsfehler bei $i = 4$ und $i = 5$.
Anhand der Stricharten erkennt man erlaubte (durchgezogene) und verbotene (punktierte) Pfeile in rot $(u_i = 0)$ und blau $(u_i = 1)$. Punktierte Linien haben einen Vergleich gegen einen Konkurrenten verloren und können nicht Teil des ausgewählten Pfades sein.
Der untere Teil der Grafik zeigt die $2^m = 4$ überlebenden Pfade ${\it \Phi}_9(S_{\mu})$ zum Zeitpunkt $i = 9$.
- Man findet diese Pfade am einfachsten von rechts nach links (Rückwärtsrichtung).
- Die folgende Angabe zeigt die durchlaufenen Zustände $S_{\mu}$ allerdings in Vorwärtsrichtung:
- $${\it \Phi}_9(S_0) \text{:} \hspace{0.4cm} S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0 → S_0,$$
- $${\it \Phi}_9(S_1) \text{:} \hspace{0.4cm} S_0 → S_0 → S_0 → S_0 → S_1 → S_2 → S_1 → S_3 → S_2 → S_1,$$
- $${\it \Phi}_9(S_2) \text{:} \hspace{0.4cm} S_0 → S_0 → S_0 → S_0 → S_1 → S_2 → S_1 → S_2 → S_1 → S_2,$$
- $${\it \Phi}_9(S_3) \text{:} \hspace{0.4cm} S_0 → S_0 → S_0 → S_0 → S_1 → S_2 → S_1 → S_2 → S_1 → S_3.$$
Zu früheren Zeitpunkten $(i<9)$ würden sich andere überlebende Pfade ${\it \Phi}_i(S_{\mu})$ ergeben. Deshalb definieren wir:
$\text{Definition:}$ Der überlebende Pfad (englisch: Survivor) ${\it \Phi}_i(S_{\mu})$ ist der durchgehende Pfad vom Start $S_0$ $($bei $i = 0)$ zum Knoten $S_{\mu}$ zum Zeitpunkt $i$. Empfehlenswert ist die Pfadsuche in Rückwärtsrichtung.
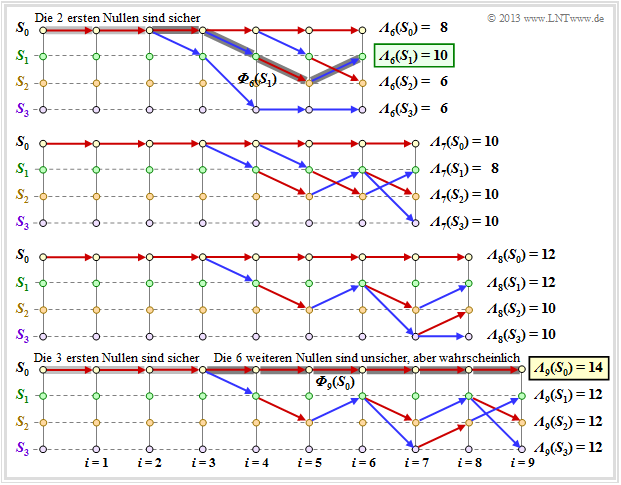
Die folgende Grafik zeigt die überlebenden Pfade für die Zeitpunkte $i = 6$ bis $i = 9$. Zusätzlich sind die jeweiligen Metriken ${\it \Lambda}_i(S_{\mu})$ für alle vier Zustände angegeben.
Diese Grafik ist wie folgt zu interpretieren:
- Zum Zeitpunkt $i = 9$ kann noch keine endgültige ML–Entscheidung über die ersten neun Bit der Informationssequenz getroffen werden. Allerdings ist bereits sicher, dass die wahrscheinlichste Bitfolge durch einen der Pfade ${\it \Phi}_9(S_0), \ \text{...} \ , \ {\it \Phi}_9(S_3)$ richtig wiedergegeben wird.
- Da alle vier Pfade bis $i = 3$ identisch sind, ist die Entscheidung "$v_1 = 0, v_2 = 0, \ v_3 = 0$" die bestmögliche (hellgraue Hinterlegung). Auch zu einem späteren Zeitpunkt würde keine andere Entscheidung getroffen werden. Hinsichtlich der Bits $v_4, \ v_5, \ \text{...}$ sollte man sich zu diesem frühen Zeitpunkt noch nicht festlegen.
- Müsste man zum Zeitpunkt $i = 9$ eine Zwangsentscheidung treffen, so würde man sich für ${\it \Phi}_9(S_0)$ ⇒ $\underline{v} = (0, 0, \ \text{...} \ , 0)$ entscheiden, da die Metrik ${\it \Lambda}_9(S_0) = 14$ größer ist als die Vergleichsmetriken.
- Die Zwangsentscheidung zum Zeitpunkt $i = 9$ führt in diesem Beispiel zum richtigen Ergebnis. Zum Zeitpunkt $i = 6$ wäre ein solcher Zwangsentscheid falsch gewesen ⇒ $\underline{v} = (0, 0, 0, 1, 0, 1)$, und zu den Zeitpunten $i = 7$ bzw. $i = 8$ nicht eindeutig.
Weitere Decodierverfahren für Faltungscodes
Wir haben uns bisher nur mit dem Viterbi–Algorithmus in der Form beschäftigt, der 1967 von Andrew J. Viterbi in [Vit67][1] veröffentlicht wurde. Erst 1974 hat George David Forney nachgewiesen, dass dieser Algorithmus eine Maximum–Likelihood–Decodierung von Faltungscodes durchführt.
Aber schon in den Jahren zuvor waren viele Wissenschaftler sehr bemüht, effiziente Decodierverfahren für die 1955 erstmals von Peter Elias beschriebenen Faltungscodes bereitzustellen. Zu nennen sind hier unter Anderem – genauere Beschreibungen findet man beispielsweise in [Bos98][2] oder der englischen Ausgabe [Bos99][3].
- Sequential Decoding von J. M. Wozencraft und B. Reiffen aus dem Jahre 1961,
- der Vorschlag von Robert Mario Fano (1963), der als Fano–Algorithmus bekannt wurde,
- die Arbeiten von Kamil Zigangirov (1966) und Frederick Jelinek (1969), deren Decodierverfahren auch als Stack–Algorithmus bezeichnet wird.
Alle diese Decodierverfahren und auch der Viterbi–Algorithmus in seiner bisher beschriebenen Form liefern "hart" entschiedene Ausgangswerte ⇒ $v_i ∈ \{0, 1\}$. Oftmals wären jedoch Informationen über die Zuverlässigkeit der getroffenen Entscheidungen wünschenswert, insbesondere dann, wenn ein verkettetes Codierschema mit einem äußeren und einem inneren Code vorliegt.
Kennt man die Zuverlässigkeit der vom inneren Decoder entschiedenen Bits zumindest grob, so kann durch diese Information die Bitfehlerwahrscheinlichkeit des äußeren Decoders (signifikant) herabgesetzt werden. Der von Joachim Hagenauer in [Hag90][4] vorgeschlagene Soft–Output–Viterbi–Algorithmus (SOVA) erlaubt es, zusätzlich zu den entschiedenen Symbolen auch jeweils ein Zuverlässigkeitsmaß anzugeben.
Abschließend gehen wir noch etwas genauer auf den BCJR–Algorithmus ein, benannt nach dessen Erfindern L. R. Bahl, J. Cocke, F. Jelinek und J. Raviv [BCJR74][5].
- Während der Viterbi–Algorithmus nur eine Schätzung der Gesamtsequenz vornimmt ⇒ block–wise ML, schätzt der BCJR–Algorithmus ein einzelnes Symbol (Bit) unter Berücksichtigung der gesamten empfangenen Codesequenz.
- Es handelt sich hierbei also um eine symbolweise Maximum–Aposteriori–Decodierung ⇒ bit–wise MAP.
$\text{Fazit:}$ Der Unterschied zwischen Viterbi–Algorithmus und BCJR–Algorithmus soll – stark vereinfacht – am Beispiel eines terminierten Faltungscodes dargestellt werden:
- Der Viterbi–Algorithmus arbeitet das Trellis nur in einer Richtung – der Vorwärtsrichtung – ab und berechnet für jeden Knoten die Metriken ${\it \Lambda}_i(S_{\mu})$. Nach Erreichen des Endknotens wird der überlebende Pfad gesucht, der die wahrscheinlichste Codesequenz kennzeichnet.
- Beim BCJR–Algorithmus wird das Trellis zweimal abgearbeitet, einmal in Vorwärtsrichtung und anschließend in Rückwärtsrichtung. Für jeden Knoten sind dann zwei Metriken angebbar, aus denen für jedes Bit die Aposterori–Wahrscheinlichkeit bestimmt werden kann.
Hinweise:
- Diese Kurzzusammenfassung basiert auf dem Lehrbüchern [Bos98][2] bzw. [Bos99][3].
- Eine etwas ausführlichere Beschreibung des BCJR–Algorithmus' folgt auf der Seite Hard Decision vs. Soft Decision im vierten Hauptkapitel "Iterative Decodierverfahren".
Aufgaben zum Kapitel
Aufgabe 3.9: Grundlegendes zum Viterbi–Algorithmus
Aufgabe 3.9Z: Nochmals Viterbi–Algorithmus
Aufgabe 3.10: Fehlergrößenberechnung
Aufgabe 3.10Z: ML–Decodierung von Faltungscodes
Aufgabe 3.11: Viterbi–Pfadsuche
Quellenverzeichnis
- ↑ Viterbi, A.J.: Error Bounds for Convolutional Codes and an Asymptotically Optimum Decoding Algorithm. In: IEEE Transactions on Information Theory, vol. IT-13, pp. 260-269, April 1967.
- ↑ 2.0 2.1 Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998.
- ↑ 3.0 3.1 Bossert, M.: Channel Coding for Telecommunications. Wiley & Sons, 1999.
- ↑ Hagenauer, J.: Soft Output Viterbi Decoder. In: Technischer Report, Deutsche Forschungsanstalt für Luft- und Raumfahrt (DLR), 1990.
- ↑ Bahl, L.R.; Cocke, J.; Jelinek, F.; Raviv, J.: Optimal Decoding of Linear Codes for Minimizing Symbol Error Rate. In: IEEE Transactions on Information Theory, Vol. IT-20, S. 284-287, 1974.