Difference between revisions of "Theory of Stochastic Signals/Two-Dimensional Random Variables"
| (69 intermediate revisions by 9 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Random Variables with Statistical Dependence |
| − | |Vorherige Seite= | + | |Vorherige Seite=Further Distributions |
| − | |Nächste Seite= | + | |Nächste Seite=Two-Dimensional Gaussian Random Variables |
}} | }} | ||
| − | + | == # OVERVIEW OF THE FOURTH MAIN CHAPTER # == | |
| + | <br> | ||
| + | Now random variables with statistical bindings are treated and illustrated by typical examples. | ||
| + | After the general description of two-dimensional random variables, we turn to | ||
| + | #the "auto-correlation function", | ||
| + | #the "cross-correlation function" | ||
| + | #and the associated spectral functions $($"power-spectral density", "cross power-spectral density"$)$. | ||
| − | |||
| − | + | Specifically, this chapter covers: | |
| − | |||
| − | + | *the statistical description of »two-dimensional random variables« using the »joint PDF«, | |
| + | *the difference between »statistical dependence« and »correlation«, | ||
| + | *the classification features »stationarity« and »ergodicity« of stochastic processes, | ||
| + | *the definitions of »auto-correlation function« $\rm (ACF)$ and »power-spectral density« $\rm (PSD)$, | ||
| + | *the definitions of »cross-correlation function« $\rm (CCF)$ and »cross power-spectral density« $\rm (C–PSD)$, | ||
| + | *the numerical determination of all these variables in the two- and multi-dimensional case. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Properties and examples== | |
| − | + | <br> | |
| − | + | As a transition to the [[Theory_of_Stochastic_Signals/Auto-Correlation_Function_(ACF)|$\text{correlation functions}$]] we now consider two random variables $x$ and $y$, between which statistical dependences exist. | |
| + | Each of these two random variables can be described on its own with the introduced characteristic variables corresponding | ||
| + | *to the second main chapter ⇒ [[Theory_of_Stochastic_Signals/From_Random_Experiment_to_Random_Variable#.23_OVERVIEW_OF_THE_SECOND_MAIN_CHAPTER_.23|"Discrete Random Variables"]] | ||
| + | *and the third main chapter ⇒ [[Theory_of_Stochastic_Signals/Probability_Density_Function#.23_OVERVIEW_OF_THE_THIRD_MAIN_CHAPTER_.23|"Continuous Random Variables"]]. | ||
| − | |||
| − | |||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ To describe the statistical dependences between two variables $x$ and $y$, it is convenient to combine the two components <br> into one »'''two-dimensional random variable'''« or »'''2D random variable'''« $(x, y)$. | ||
| + | *The individual components can be signals such as the real and imaginary parts of a phase modulated signal. | ||
| + | *But there are a variety of two-dimensional random variables in other domains as well, as the following example will show.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | + | {{GraueBox|TEXT= |
| − | + | $\text{Example 1:}$ The left diagram is from the random experiment "Throwing two dice". | |
| − | + | [[File: P_ID162__Sto_T_4_1_S1_neu.png |frame| Two examples of statistically dependent random variables]] | |
| − | |||
| − | |||
| − | |||
| − | + | *Plotted to the right is the number of the first die $(W_1)$, | |
| + | *plotted to the top is the sum $S$ of both dice. | ||
| − | |||
| − | |||
| − | |||
| − | + | The two components here are each discrete random variables between which there are statistical dependencies: | |
| + | *If $W_1 = 1$, then the sum $S$ can only take values between $2$ and $7$, each with equal probability. | ||
| + | *In contrast, for $W_1 = 6$ all values between $7$ and $12$ are possible, also with equal probability. | ||
| − | == | + | |
| − | {{Definition}}''' | + | |
| − | $$F_{xy}(r_{x},r_{y}) = {\rm Pr}\ | + | In the right diagram, the maximum temperatures of the $31$ days in May 2002 of Munich (to the top) and the mountain "Zugspitze" (to the right) are contrasted. Both random variables are continuous in value: |
| − | + | *Although the measurement points are about $\text{100 km}$ apart, and on the Zugspitze, it is on average about $20$ degrees colder than in Munich due to the different altitudes $($nearly $3000$ versus $520$ meters$)$, one recognizes nevertheless a certain statistical dependence between the two random variables ${\it Θ}_{\rm M}$ and ${\it Θ}_{\rm Z}$. | |
| − | + | *If it is warm in Munich, then pleasant temperatures are also more likely to be expected on the Zugspitze. However, the relationship is not deterministic: The coldest day in May 2002 was a different day in Munich than the coldest day on the Zugspitze. }} | |
| − | * | + | |
| − | :$$F_{xy}(r_{x},r_{y})=\int_{-\infty}^{r_{y}} \int_{-\infty}^{r_{x}} f_{xy}(x,y) \,\,{\rm d}x \,\, {\rm d}y | + | ==Joint probability density function== |
| − | * | + | <br> |
| + | We restrict ourselves here mostly to continuous valued random variables. | ||
| + | *However, sometimes the peculiarities of two-dimensional discrete random variables are discussed in more detail. | ||
| + | *Most of the characteristics previously defined for one-dimensional random variables can be easily extended to two-dimensional variables. | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ | ||
| + | The probability density function $\rm (PDF)$ of the two-dimensional random variable at the location $(x_\mu,\hspace{0.1cm} y_\mu)$ ⇒ »'''joint PDF'''« or »'''2D–PDF'''« <br>is an extension of the one-dimensional PDF $(∩$ denotes logical "and" operation$)$: | ||
| + | :$$f_{xy}(x_\mu, \hspace{0.1cm}y_\mu) = \lim_{\left.{\Delta x\rightarrow 0 \atop {\Delta y\rightarrow 0} }\right.}\frac{ {\rm Pr}\big [ (x_\mu - {\rm \Delta} x/{\rm 2} \le x \le x_\mu + {\rm \Delta} x/{\rm 2}) \cap (y_\mu - {\rm \Delta} y/{\rm 2} \le y \le y_\mu +{\rm \Delta}y/{\rm 2}) \big] }{ {\rm \Delta} \ x\cdot{\rm \Delta} y}.$$ | ||
| + | $\rm Note$: | ||
| + | *If the two-dimensional random variable is discrete, the definition must be slightly modified: | ||
| + | *For the lower range limits, the "less-than-equal" sign must then be replaced by "less-than" according to the section [[Theory_of_Stochastic_Signals/Cumulative_Distribution_Function#CDF_for_discrete-valued_random_variables|"CDF for discrete-valued random variables"]]. }} | ||
| + | |||
| + | |||
| + | Using this joint PDF $f_{xy}(x, y)$, statistical dependencies within the two-dimensional random variable $(x,\ y)$ are also fully captured in contrast to the two one-dimensional density functions ⇒ »'''marginal probability density functions'''« $($or "edge probability density functions"$)$: | ||
| + | :$$f_{x}(x) = \int _{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}y ,$$ | ||
| + | :$$f_{y}(y) = \int_{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}x .$$ | ||
| + | |||
| + | These two marginal probability density functions $f_x(x)$ and $f_y(y)$ | ||
| + | *provide only statistical information about the individual components $x$ and $y$, resp. | ||
| + | *but not about the statistical bindings between them. | ||
| + | |||
| + | |||
| + | ==Two-dimensional cumulative distribution function== | ||
| + | <br> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ Like the "2D–PDF", the »'''2D cumulative distribution function'''« is merely a useful extension of the [[Theory_of_Stochastic_Signals/Cumulative_Distribution_Function#CDF_for_continuous-valued_random_variables|$\text{one-dimensional distribution function}$]] $\rm (CDF)$: | ||
| + | :$$F_{xy}(r_{x},r_{y}) = {\rm Pr}\big [(x \le r_{x}) \cap (y \le r_{y}) \big ] .$$}} | ||
| + | |||
| + | |||
| + | The following similarities and differences between the "1D–CDF" and the 2D–CDF" emerge: | ||
| + | *The functional relationship between two-dimensional PDF and two-dimensional CDF is given by integration as in the one-dimensional case, but now in two dimensions. For continuous valued random variables: | ||
| + | :$$F_{xy}(r_{x},r_{y})=\int_{-\infty}^{r_{y}} \int_{-\infty}^{r_{x}} f_{xy}(x,y) \,\,{\rm d}x \,\, {\rm d}y .$$ | ||
| + | *Inversely, the probability density function can be given from the cumulative distribution function by partial differentiation to $r_{x}$ and $r_{y}$: | ||
:$$f_{xy}(x,y)=\frac{{\rm d}^{\rm 2} F_{xy}(r_{x},r_{y})}{{\rm d} r_{x} \,\, {\rm d} r_{y}}\Bigg|_{\left.{r_{x}=x \atop {r_{y}=y}}\right.}.$$ | :$$f_{xy}(x,y)=\frac{{\rm d}^{\rm 2} F_{xy}(r_{x},r_{y})}{{\rm d} r_{x} \,\, {\rm d} r_{y}}\Bigg|_{\left.{r_{x}=x \atop {r_{y}=y}}\right.}.$$ | ||
| − | * | + | *Relative to the two-dimensional cumulative distribution function $F_{xy}(r_{x}, r_{y})$ the following limits apply: |
:$$F_{xy}(-\infty,-\infty) = 0,$$ | :$$F_{xy}(-\infty,-\infty) = 0,$$ | ||
| − | :$$F_{xy}(r_{\rm x},\infty)=F_{x}(r_{x} ),$$ | + | :$$F_{xy}(r_{\rm x},+\infty)=F_{x}(r_{x} ),$$ |
| − | :$$F_{xy}(\infty,r_{y})=F_{y}(r_{y} ) ,$$ | + | :$$F_{xy}(+\infty,r_{y})=F_{y}(r_{y} ) ,$$ |
| − | :$$F_{xy}(\infty,\infty) = 1.$$ | + | :$$F_{xy} (+\infty,+\infty) = 1.$$ |
| − | * | + | *From the last equation $($infinitely large $r_{x}$ and $r_{y})$ we obtain the »'''normalization condition'''« for the "2D– PDF": |
| − | :$$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}x \,\,{\rm d}y=1 . | + | :$$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}x \,\,{\rm d}y=1 . $$ |
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Conclusion:}$ Note the significant difference between one-dimensional and two-dimensional random variables: | ||
| + | *For one-dimensional random variables, the area under the PDF always yields the value $1$. | ||
| + | *For two-dimensional random variables, the PDF volume is always equal to $1$.}} | ||
| + | |||
| + | ==PDF for statistically independent components== | ||
| + | <br> | ||
| + | For statistically independent components $x$, $y$ the following holds for the joint probability according to the elementary laws of statistics if $x$ and $y$ are continuous in value: | ||
| + | :$${\rm Pr} \big[(x_{\rm 1}\le x \le x_{\rm 2}) \cap( y_{\rm 1}\le y\le y_{\rm 2})\big] ={\rm Pr} (x_{\rm 1}\le x \le x_{\rm 2}) \cdot {\rm Pr}(y_{\rm 1}\le y\le y_{\rm 2}) .$$ | ||
| + | For this, in the case of independent components can also be written: | ||
| + | :$${\rm Pr} \big[(x_{\rm 1}\le x \le x_{\rm 2}) \cap(y_{\rm 1}\le y\le y_{\rm 2})\big] =\int _{x_{\rm 1}}^{x_{\rm 2}}f_{x}(x) \,{\rm d}x\cdot \int_{y_{\rm 1}}^{y_{\rm 2}} f_{y}(y) \, {\rm d}y.$$ | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ It follows that for »'''statistical independence'''« the following condition must be satisfied with respect to the »'''two-dimensional probability density function'''«: | ||
| + | :$$f_{xy}(x,y)=f_{x}(x) \cdot f_y(y) .$$}} | ||
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 2:}$ In the graph, the instantaneous values of a two-dimensional random variable are plotted as points in the $(x,\, y)$–plane. | ||
| + | *Ranges with many points, which accordingly appear dark, indicate large values of the two-dimensional PDF $f_{xy}(x,\, y)$. | ||
| + | *In contrast, the random variable $(x,\, y)$ has relatively few components in rather bright areas. | ||
| + | |||
| + | [[File:P_ID153__Sto_T_4_1_S4_nochmals_neu.png |frame| Statistically independent components: $f_{xy}(x, y)$, $f_{x}(x)$ and $f_{y}(y)$]] | ||
| + | <br> | ||
| + | The graph can be interpreted as follows: | ||
| + | *The marginal probability densities $f_{x}(x)$ and $f_{y}(y)$ already indicate that both $x$ and $y$ are Gaussian and zero mean, and that the random variable $x$ has a larger standard deviation than $y$. | ||
| + | *$f_{x}(x)$ and $f_{y}(y)$ do not provide information on whether or not statistical bindings exist for the random variable $(x,\, y)$. | ||
| + | *However, using the "2D-PDF" $f_{xy}(x,\, y)$ one can see that here there are no statistical bindings between the two components $x$ and $y$. | ||
| + | *With statistical independence, any cut through $f_{xy}(x, y)$ parallel to $y$–axis yields a function that is equal in shape to the marginal PDF $f_{y}(y)$. Similarly, all cuts parallel to $x$–axis are equal in shape to $f_{x}(x)$. | ||
| + | *This fact is equivalent to saying that in this example $f_{xy}(x,\, y)$ can be represented as the product of the two marginal probability densities: | ||
| + | :$$f_{xy}(x,\, y)=f_{x}(x) \cdot f_y(y) .$$}} | ||
| + | |||
| + | ==PDF for statistically dependent components== | ||
| + | <br> | ||
| + | If there are statistical bindings between $x$ and $y$, then different cuts parallel to $x$– and $y$–axis, resp., yield different (non-shape equivalent) functions. In this case, of course, the joint PDF cannot be described as a product of the two (one-dimensional) marginal probability densities functions either. | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 3:}$ The graph shows the instantaneous values of a two-dimensional random variable in the $(x, y)$–plane. | ||
| + | [[File:P_ID156__Sto_T_4_1_S5_neu.png |right|frame|Statistically dependent components: $f_{xy}(x, y)$, $f_{x}(x)$, $f_{y}(y)$ ]] | ||
| + | <br>Now, unlike $\text{Example 2}$ there are statistical bindings between $x$ and $y$. | ||
| + | *The two-dimensional random variable takes all "2D" values with equal probability in the parallelogram drawn in blue. | ||
| + | *No values are possible outside the parallelogram. | ||
| + | |||
| + | |||
| + | <br>One recognizes from this representation: | ||
| + | #Integration over $f_{xy}(x, y)$ parallel to the $x$–axis leads to the triangular marginal PDF $f_{y}(y)$, integration parallel to $y$–axis to the trapezoidal PDF $f_{x}(x)$. | ||
| + | #From the joint PDF $f_{xy}(x, y)$ it can already be guessed that for each $x$–value on statistical average, a different $y$–value is to be expected. | ||
| + | #This means that the components $x$ and $y$ are statistically dependent on each other. }} | ||
| + | |||
| + | ==Expected values of two-dimensional random variables== | ||
| + | <br> | ||
| + | A special case of statistical dependence is "correlation". | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ Under »'''correlation'''« one understands a "linear dependence" between the individual components $x$ and $y$. | ||
| + | *Correlated random variables are thus always also statistically dependent. | ||
| + | *But not every statistical dependence implies correlation at the same time.}} | ||
| + | |||
| − | + | To quantitatively capture correlation, one uses various expected values of the two-dimensional random variable $(x, y)$. | |
| − | |||
| − | |||
| − | + | These are defined analogously to the one-dimensional case, | |
| − | + | *according to [[Theory_of_Stochastic_Signals/Moments_of_a_Discrete_Random_Variable|"Chapter 2"]] (for discrete valued random variables). | |
| − | + | *and [[Theory_of_Stochastic_Signals/Expected_Values_and_Moments|"Chapter 3"]] (for continuous valued random variables): | |
| − | + | ||
| − | |||
| − | |||
| − | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ For the (non-centered) »'''moments'''« the following relation holds: | ||
| + | :$$m_{kl}={\rm E}\big[x^k\cdot y^l\big]=\int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x\hspace{0.05cm}^{k} \cdot y\hspace{0.05cm}^{l} \cdot f_{xy}(x,y) \, {\rm d}x\, {\rm d}y.$$ | ||
| + | Thus, the two linear means are $m_x = m_{10}$ and $m_y = m_{01}.$ }} | ||
| − | |||
| − | [ | + | {{BlaueBox|TEXT= |
| + | $\text{Definition:}$ The »'''central moments'''« $($related to $m_x$ and $m_y)$ are: | ||
| + | :$$\mu_{kl} = {\rm E}\big[(x-m_{x})\hspace{0.05cm}^k \cdot (y-m_{y})\hspace{0.05cm}^l\big] .$$ | ||
| + | In this general definition equation, the variances $σ_x^2$ and $σ_y^2$ of the two individual components are included by $\mu_{20}$ and $\mu_{02}$, resp. }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | {{BlaueBox|TEXT= |
| − | + | $\text{Definition:}$ Of particular importance is the »'''covariance'''« $(k = l = 1)$, which is a measure of the "linear statistical dependence" between the variables $x$ and $y$: | |
| + | :$$\mu_{11} = {\rm E}\big[(x-m_{x})\cdot(y-m_{y})\big] = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} (x-m_{x}) \cdot (y-m_{y})\cdot f_{xy}(x,y) \,{\rm d}x \, {\rm d}y .$$ | ||
| + | In the following, we also denote the covariance $\mu_{11}$ in part by "$\mu_{xy}$", if the covariance refers to the random variables $x$ and $y$.}} | ||
| − | |||
| − | |||
| − | [ | + | Notes: |
| + | *The covariance $\mu_{11}=\mu_{xy}$ is related to the non-centered moment $m_{11} = m_{xy} = {\rm E}\big[x \cdot y\big]$ as follows: | ||
| + | :$$\mu_{xy} = m_{xy} -m_{x }\cdot m_{y}.$$ | ||
| − | + | *This equation is enormously advantageous for numerical evaluations, since $m_{xy}$, $m_x$ and $m_y$ can be found from the sequences $〈x_v〉$ and $〈y_v〉$ in a single run. | |
| + | *On the other hand, if one were to calculate the covariance $\mu_{xy}$ according to the above definition equation, one would have to find the mean values $m_x$ and $m_y$ in a first run and could then only calculate the expected value ${\rm E}\big[(x - m_x) \cdot (y - m_y)\big]$ in a second run. | ||
| − | |||
| − | |||
| − | = | + | {{GraueBox|TEXT= |
| − | + | $\text{Example 4:}$ In the first two rows of the table, the first elements of two random sequences $〈x_ν〉$ and $〈y_ν〉$ are entered. In the last row, the respective products $x_ν - y_ν$ are given. | |
| − | * | + | [[File:P_ID628__Sto_T_4_1_S6Neu.png |right|frame|Example for two-dimensional expected values]] |
| − | * | + | *By averaging over ten sequence elements in each case, one obtains |
| + | :$$m_x =0.5,\ \ m_y = 1, \ \ m_{xy} = 0.69.$$ | ||
| + | *This directly results in the value for the covariance: | ||
| + | :$$\mu_{xy} = 0.69 - 0.5 · 1 = 0.19.$$ | ||
| + | Without knowledge of the equation $\mu_{xy} = m_{xy} - m_x\cdot m_y$ one would have had to first determine the means $m_x$ and $m_y$ in the first run, and then determine the covariance $\mu_{xy}$ as the expected value of the product of the zero mean variables in a second run.}} | ||
| − | + | ==Correlation coefficient== | |
| − | + | <br> | |
| − | + | With statistical independence of the two components $x$ and $y$ the covariance $\mu_{xy} \equiv 0$. This case has already been considered in $\text{Example 2}$ in the section [[Theory_of_Stochastic_Signals/Two-Dimensional_Random_Variables#PDF_for_statistically_independent_components|"PDF for statistically independent components"]]. | |
| − | |||
| − | |||
| − | $ | ||
| − | |||
| − | |||
| − | |||
| + | *But the result $\mu_{xy} = 0$ is also possible for statistically dependent components $x$ and $y$ namely when they are uncorrelated, i.e. "linearly independent". | ||
| + | *The statistical dependence is then not of first order, but of higher order, for example corresponding to the equation $y=x^2.$ | ||
| − | |||
| − | |||
| − | |||
| − | + | One speaks of »'''complete correlation'''« when the (deterministic) dependence between $x$ and $y$ is expressed by the equation $y = K · x$. Then the covariance is given by: | |
| − | { | + | * $\mu_{xy} = σ_x · σ_y$ with positive $K$ value, |
| − | + | * $\mu_{xy} = - σ_x · σ_y$ with negative $K$ value. | |
| − | + | Therefore, instead of the "covariance" one often uses the so-called "correlation coefficient" as descriptive quantity. | |
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ The »'''correlation coefficient'''« is the quotient of the covariance $\mu_{xy}$ and the product of the standard deviations $σ_x$ and $σ_y$ of the two components: | ||
| + | :$$\rho_{xy}=\frac{\mu_{xy} }{\sigma_x \cdot \sigma_y}.$$}} | ||
| − | |||
| − | |||
| + | The correlation coefficient $\rho_{xy}$ has the following properties: | ||
| + | *Because of normalization, $-1 \le ρ_{xy} ≤ +1$ always holds. | ||
| + | *If the two random variables $x$ and $y$ are uncorrelated, then $ρ_{xy} = 0$. | ||
| + | *For strict linear dependence between $x$ and $y$ ⇒ $ρ_{xy}= ±1$ ⇒ complete correlation. | ||
| + | *A positive correlation coefficient means that when $x$ is larger, on statistical average, $y$ is also larger than when $x$ is smaller. | ||
| + | *In contrast, a negative correlation coefficient expresses that $y$ becomes smaller on average as $x$ increases. | ||
| − | |||
| − | = | + | {{GraueBox|TEXT= |
| − | + | [[File:P_ID232__Sto_T_4_1_S7a_neu.png |right|frame| Two-dimensional Gaussian PDF with correlation]] | |
| + | $\text{Example 5:}$ The following conditions apply: | ||
| + | #The considered components $x$ and $y$ each have a Gaussian PDF. | ||
| + | #The two standard deviations are different $(σ_y < σ_x)$. | ||
| + | #The correlation coefficient is $ρ_{xy} = 0.8$. | ||
| − | |||
| − | |||
| − | + | Unlike [[Theory_of_Stochastic_Signals/Two-Dimensional_Random_Variables#PDF_for_statistically_independent_components|$\text{Example 2}$]] with statistically independent components ⇒ $ρ_{xy} = 0$ $($even though $σ_y < σ_x)$ one recognizes that here | |
| − | + | *with larger $x$–value, on statistical average, $y$ is also larger | |
| − | + | *than with a smaller $x$–value.}} | |
| − | * | ||
| − | {{ | + | ==Regression line== |
| − | + | <br> | |
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ The »'''regression line'''« – sometimes called "correlation line" – is the straight line $y = K(x)$ in the $(x, y)$–plane through the "midpoint" $(m_x, m_y)$. | ||
| + | [[File: EN_Sto_T_4_1_S7neu.png |frame|Two-dimensional Gaussian PDF with regression line $\rm (RL)$ ]] | ||
| + | The regression line has the following properties: | ||
| − | [ | + | *The mean square deviation from this straight line - viewed in $y$–direction and averaged over all $N$ points - is minimal: |
| + | :$$\overline{\varepsilon_y^{\rm 2} }=\frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}\; \;\big [y_\nu - K(x_{\nu})\big ]^{\rm 2}={\rm minimum}.$$ | ||
| + | *The regression line can be interpreted as a kind of "statistical symmetry axis". The equation of the straight line is: | ||
| + | :$$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x - m_x)+m_y.$$ | ||
| + | *The angle taken by the regression line to the $x$–axis is: | ||
| + | :$$\theta_{y\hspace{0.05cm}\rightarrow \hspace{0.05cm}x}={\rm arctan}\ (\frac{\sigma_{y} }{\sigma_{x} }\cdot \rho_{xy}).$$}} | ||
| − | |||
| − | |||
| + | By this nomenclature it should be made clear that we are dealing here with the regression of $y$ on $x$. | ||
| − | + | *The regression in the opposite direction – that is, from $x$ to $y$ – on the other hand, means the minimization of the mean square deviation in $x$–direction. | |
| − | * | ||
| − | |||
| − | + | *The (German language) applet [[Applets:Korrelation_und_Regressionsgerade|"Korrelation und Regressionsgerade"]] ⇒ "Correlation Coefficient and Regression Line" illustrates <br>that in general $($if $σ_y \ne σ_x)$ for the regression of $x$ on $y$ will result in a different angle and thus a different regression line: | |
| − | + | :$$\theta_{x\hspace{0.05cm}\rightarrow \hspace{0.05cm} y}={\rm arctan}\ (\frac{\sigma_{x}}{\sigma_{y}}\cdot \rho_{xy}).$$ | |
| − | |||
| − | + | ==Exercises for the chapter== | |
| − | + | <br> | |
| − | + | [[Aufgaben:Exercise_4.1:_Triangular_(x,_y)_Area|Exercise 4.1: Triangular (x, y) Area]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[Aufgaben:Exercise_4.1Z:_Appointment_to_Breakfast|Exercise 4.1Z: Appointment to Breakfast]] | ||
| − | + | [[Aufgaben:Exercise_4.2:_Triangle_Area_again|Exercise 4.2: Triangle Area again]] | |
| − | + | [[Aufgaben:Exercise_4.2Z:_Correlation_between_"x"_and_"e_to_the_Power_of_x"|Exercise 4.2Z: Correlation between "x" and "e to the Power of x"]] | |
| − | |||
| − | + | [[Aufgaben:Exercise_4.3:_Algebraic_and_Modulo_Sum|Exercise 4.3: Algebraic and Modulo Sum]] | |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.3Z:_Dirac-shaped_2D_PDF|Exercise 4.3Z: Dirac-shaped 2D PDF]] |
| − | |||
{{Display}} | {{Display}} | ||
Latest revision as of 14:38, 21 December 2022
Contents
- 1 # OVERVIEW OF THE FOURTH MAIN CHAPTER #
- 2 Properties and examples
- 3 Joint probability density function
- 4 Two-dimensional cumulative distribution function
- 5 PDF for statistically independent components
- 6 PDF for statistically dependent components
- 7 Expected values of two-dimensional random variables
- 8 Correlation coefficient
- 9 Regression line
- 10 Exercises for the chapter
# OVERVIEW OF THE FOURTH MAIN CHAPTER #
Now random variables with statistical bindings are treated and illustrated by typical examples.
After the general description of two-dimensional random variables, we turn to
- the "auto-correlation function",
- the "cross-correlation function"
- and the associated spectral functions $($"power-spectral density", "cross power-spectral density"$)$.
Specifically, this chapter covers:
- the statistical description of »two-dimensional random variables« using the »joint PDF«,
- the difference between »statistical dependence« and »correlation«,
- the classification features »stationarity« and »ergodicity« of stochastic processes,
- the definitions of »auto-correlation function« $\rm (ACF)$ and »power-spectral density« $\rm (PSD)$,
- the definitions of »cross-correlation function« $\rm (CCF)$ and »cross power-spectral density« $\rm (C–PSD)$,
- the numerical determination of all these variables in the two- and multi-dimensional case.
Properties and examples
As a transition to the $\text{correlation functions}$ we now consider two random variables $x$ and $y$, between which statistical dependences exist.
Each of these two random variables can be described on its own with the introduced characteristic variables corresponding
- to the second main chapter ⇒ "Discrete Random Variables"
- and the third main chapter ⇒ "Continuous Random Variables".
$\text{Definition:}$ To describe the statistical dependences between two variables $x$ and $y$, it is convenient to combine the two components
into one »two-dimensional random variable« or »2D random variable« $(x, y)$.
- The individual components can be signals such as the real and imaginary parts of a phase modulated signal.
- But there are a variety of two-dimensional random variables in other domains as well, as the following example will show.
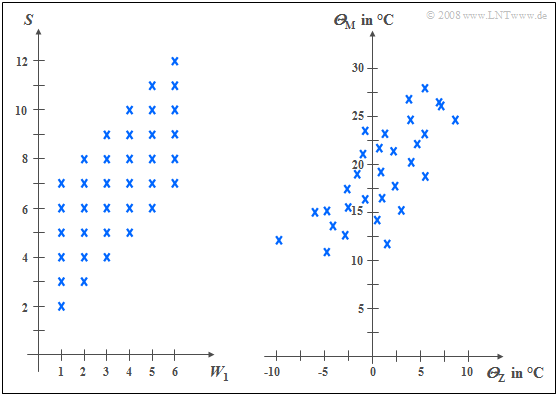
$\text{Example 1:}$ The left diagram is from the random experiment "Throwing two dice".
- Plotted to the right is the number of the first die $(W_1)$,
- plotted to the top is the sum $S$ of both dice.
The two components here are each discrete random variables between which there are statistical dependencies:
- If $W_1 = 1$, then the sum $S$ can only take values between $2$ and $7$, each with equal probability.
- In contrast, for $W_1 = 6$ all values between $7$ and $12$ are possible, also with equal probability.
In the right diagram, the maximum temperatures of the $31$ days in May 2002 of Munich (to the top) and the mountain "Zugspitze" (to the right) are contrasted. Both random variables are continuous in value:
- Although the measurement points are about $\text{100 km}$ apart, and on the Zugspitze, it is on average about $20$ degrees colder than in Munich due to the different altitudes $($nearly $3000$ versus $520$ meters$)$, one recognizes nevertheless a certain statistical dependence between the two random variables ${\it Θ}_{\rm M}$ and ${\it Θ}_{\rm Z}$.
- If it is warm in Munich, then pleasant temperatures are also more likely to be expected on the Zugspitze. However, the relationship is not deterministic: The coldest day in May 2002 was a different day in Munich than the coldest day on the Zugspitze.
Joint probability density function
We restrict ourselves here mostly to continuous valued random variables.
- However, sometimes the peculiarities of two-dimensional discrete random variables are discussed in more detail.
- Most of the characteristics previously defined for one-dimensional random variables can be easily extended to two-dimensional variables.
$\text{Definition:}$
The probability density function $\rm (PDF)$ of the two-dimensional random variable at the location $(x_\mu,\hspace{0.1cm} y_\mu)$ ⇒ »joint PDF« or »2D–PDF«
is an extension of the one-dimensional PDF $(∩$ denotes logical "and" operation$)$:
- $$f_{xy}(x_\mu, \hspace{0.1cm}y_\mu) = \lim_{\left.{\Delta x\rightarrow 0 \atop {\Delta y\rightarrow 0} }\right.}\frac{ {\rm Pr}\big [ (x_\mu - {\rm \Delta} x/{\rm 2} \le x \le x_\mu + {\rm \Delta} x/{\rm 2}) \cap (y_\mu - {\rm \Delta} y/{\rm 2} \le y \le y_\mu +{\rm \Delta}y/{\rm 2}) \big] }{ {\rm \Delta} \ x\cdot{\rm \Delta} y}.$$
$\rm Note$:
- If the two-dimensional random variable is discrete, the definition must be slightly modified:
- For the lower range limits, the "less-than-equal" sign must then be replaced by "less-than" according to the section "CDF for discrete-valued random variables".
Using this joint PDF $f_{xy}(x, y)$, statistical dependencies within the two-dimensional random variable $(x,\ y)$ are also fully captured in contrast to the two one-dimensional density functions ⇒ »marginal probability density functions« $($or "edge probability density functions"$)$:
- $$f_{x}(x) = \int _{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}y ,$$
- $$f_{y}(y) = \int_{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}x .$$
These two marginal probability density functions $f_x(x)$ and $f_y(y)$
- provide only statistical information about the individual components $x$ and $y$, resp.
- but not about the statistical bindings between them.
Two-dimensional cumulative distribution function
$\text{Definition:}$ Like the "2D–PDF", the »2D cumulative distribution function« is merely a useful extension of the $\text{one-dimensional distribution function}$ $\rm (CDF)$:
- $$F_{xy}(r_{x},r_{y}) = {\rm Pr}\big [(x \le r_{x}) \cap (y \le r_{y}) \big ] .$$
The following similarities and differences between the "1D–CDF" and the 2D–CDF" emerge:
- The functional relationship between two-dimensional PDF and two-dimensional CDF is given by integration as in the one-dimensional case, but now in two dimensions. For continuous valued random variables:
- $$F_{xy}(r_{x},r_{y})=\int_{-\infty}^{r_{y}} \int_{-\infty}^{r_{x}} f_{xy}(x,y) \,\,{\rm d}x \,\, {\rm d}y .$$
- Inversely, the probability density function can be given from the cumulative distribution function by partial differentiation to $r_{x}$ and $r_{y}$:
- $$f_{xy}(x,y)=\frac{{\rm d}^{\rm 2} F_{xy}(r_{x},r_{y})}{{\rm d} r_{x} \,\, {\rm d} r_{y}}\Bigg|_{\left.{r_{x}=x \atop {r_{y}=y}}\right.}.$$
- Relative to the two-dimensional cumulative distribution function $F_{xy}(r_{x}, r_{y})$ the following limits apply:
- $$F_{xy}(-\infty,-\infty) = 0,$$
- $$F_{xy}(r_{\rm x},+\infty)=F_{x}(r_{x} ),$$
- $$F_{xy}(+\infty,r_{y})=F_{y}(r_{y} ) ,$$
- $$F_{xy} (+\infty,+\infty) = 1.$$
- From the last equation $($infinitely large $r_{x}$ and $r_{y})$ we obtain the »normalization condition« for the "2D– PDF":
- $$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}x \,\,{\rm d}y=1 . $$
$\text{Conclusion:}$ Note the significant difference between one-dimensional and two-dimensional random variables:
- For one-dimensional random variables, the area under the PDF always yields the value $1$.
- For two-dimensional random variables, the PDF volume is always equal to $1$.
PDF for statistically independent components
For statistically independent components $x$, $y$ the following holds for the joint probability according to the elementary laws of statistics if $x$ and $y$ are continuous in value:
- $${\rm Pr} \big[(x_{\rm 1}\le x \le x_{\rm 2}) \cap( y_{\rm 1}\le y\le y_{\rm 2})\big] ={\rm Pr} (x_{\rm 1}\le x \le x_{\rm 2}) \cdot {\rm Pr}(y_{\rm 1}\le y\le y_{\rm 2}) .$$
For this, in the case of independent components can also be written:
- $${\rm Pr} \big[(x_{\rm 1}\le x \le x_{\rm 2}) \cap(y_{\rm 1}\le y\le y_{\rm 2})\big] =\int _{x_{\rm 1}}^{x_{\rm 2}}f_{x}(x) \,{\rm d}x\cdot \int_{y_{\rm 1}}^{y_{\rm 2}} f_{y}(y) \, {\rm d}y.$$
$\text{Definition:}$ It follows that for »statistical independence« the following condition must be satisfied with respect to the »two-dimensional probability density function«:
- $$f_{xy}(x,y)=f_{x}(x) \cdot f_y(y) .$$
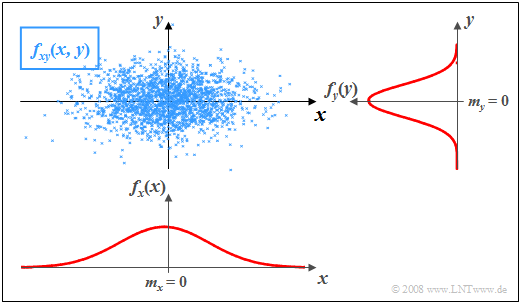
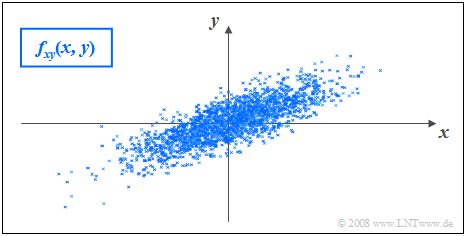
$\text{Example 2:}$ In the graph, the instantaneous values of a two-dimensional random variable are plotted as points in the $(x,\, y)$–plane.
- Ranges with many points, which accordingly appear dark, indicate large values of the two-dimensional PDF $f_{xy}(x,\, y)$.
- In contrast, the random variable $(x,\, y)$ has relatively few components in rather bright areas.
The graph can be interpreted as follows:
- The marginal probability densities $f_{x}(x)$ and $f_{y}(y)$ already indicate that both $x$ and $y$ are Gaussian and zero mean, and that the random variable $x$ has a larger standard deviation than $y$.
- $f_{x}(x)$ and $f_{y}(y)$ do not provide information on whether or not statistical bindings exist for the random variable $(x,\, y)$.
- However, using the "2D-PDF" $f_{xy}(x,\, y)$ one can see that here there are no statistical bindings between the two components $x$ and $y$.
- With statistical independence, any cut through $f_{xy}(x, y)$ parallel to $y$–axis yields a function that is equal in shape to the marginal PDF $f_{y}(y)$. Similarly, all cuts parallel to $x$–axis are equal in shape to $f_{x}(x)$.
- This fact is equivalent to saying that in this example $f_{xy}(x,\, y)$ can be represented as the product of the two marginal probability densities:
- $$f_{xy}(x,\, y)=f_{x}(x) \cdot f_y(y) .$$
PDF for statistically dependent components
If there are statistical bindings between $x$ and $y$, then different cuts parallel to $x$– and $y$–axis, resp., yield different (non-shape equivalent) functions. In this case, of course, the joint PDF cannot be described as a product of the two (one-dimensional) marginal probability densities functions either.
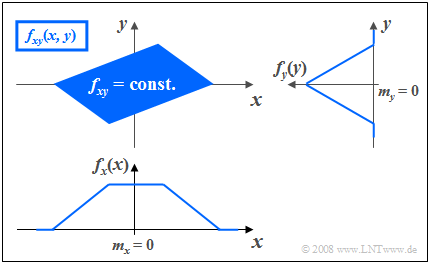
$\text{Example 3:}$ The graph shows the instantaneous values of a two-dimensional random variable in the $(x, y)$–plane.
Now, unlike $\text{Example 2}$ there are statistical bindings between $x$ and $y$.
- The two-dimensional random variable takes all "2D" values with equal probability in the parallelogram drawn in blue.
- No values are possible outside the parallelogram.
One recognizes from this representation:
- Integration over $f_{xy}(x, y)$ parallel to the $x$–axis leads to the triangular marginal PDF $f_{y}(y)$, integration parallel to $y$–axis to the trapezoidal PDF $f_{x}(x)$.
- From the joint PDF $f_{xy}(x, y)$ it can already be guessed that for each $x$–value on statistical average, a different $y$–value is to be expected.
- This means that the components $x$ and $y$ are statistically dependent on each other.
Expected values of two-dimensional random variables
A special case of statistical dependence is "correlation".
$\text{Definition:}$ Under »correlation« one understands a "linear dependence" between the individual components $x$ and $y$.
- Correlated random variables are thus always also statistically dependent.
- But not every statistical dependence implies correlation at the same time.
To quantitatively capture correlation, one uses various expected values of the two-dimensional random variable $(x, y)$.
These are defined analogously to the one-dimensional case,
- according to "Chapter 2" (for discrete valued random variables).
- and "Chapter 3" (for continuous valued random variables):
$\text{Definition:}$ For the (non-centered) »moments« the following relation holds:
- $$m_{kl}={\rm E}\big[x^k\cdot y^l\big]=\int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x\hspace{0.05cm}^{k} \cdot y\hspace{0.05cm}^{l} \cdot f_{xy}(x,y) \, {\rm d}x\, {\rm d}y.$$
Thus, the two linear means are $m_x = m_{10}$ and $m_y = m_{01}.$
$\text{Definition:}$ The »central moments« $($related to $m_x$ and $m_y)$ are:
- $$\mu_{kl} = {\rm E}\big[(x-m_{x})\hspace{0.05cm}^k \cdot (y-m_{y})\hspace{0.05cm}^l\big] .$$
In this general definition equation, the variances $σ_x^2$ and $σ_y^2$ of the two individual components are included by $\mu_{20}$ and $\mu_{02}$, resp.
$\text{Definition:}$ Of particular importance is the »covariance« $(k = l = 1)$, which is a measure of the "linear statistical dependence" between the variables $x$ and $y$:
- $$\mu_{11} = {\rm E}\big[(x-m_{x})\cdot(y-m_{y})\big] = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} (x-m_{x}) \cdot (y-m_{y})\cdot f_{xy}(x,y) \,{\rm d}x \, {\rm d}y .$$
In the following, we also denote the covariance $\mu_{11}$ in part by "$\mu_{xy}$", if the covariance refers to the random variables $x$ and $y$.
Notes:
- The covariance $\mu_{11}=\mu_{xy}$ is related to the non-centered moment $m_{11} = m_{xy} = {\rm E}\big[x \cdot y\big]$ as follows:
- $$\mu_{xy} = m_{xy} -m_{x }\cdot m_{y}.$$
- This equation is enormously advantageous for numerical evaluations, since $m_{xy}$, $m_x$ and $m_y$ can be found from the sequences $〈x_v〉$ and $〈y_v〉$ in a single run.
- On the other hand, if one were to calculate the covariance $\mu_{xy}$ according to the above definition equation, one would have to find the mean values $m_x$ and $m_y$ in a first run and could then only calculate the expected value ${\rm E}\big[(x - m_x) \cdot (y - m_y)\big]$ in a second run.
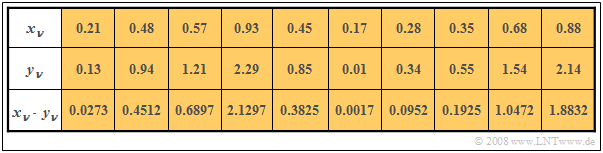
$\text{Example 4:}$ In the first two rows of the table, the first elements of two random sequences $〈x_ν〉$ and $〈y_ν〉$ are entered. In the last row, the respective products $x_ν - y_ν$ are given.
- By averaging over ten sequence elements in each case, one obtains
- $$m_x =0.5,\ \ m_y = 1, \ \ m_{xy} = 0.69.$$
- This directly results in the value for the covariance:
- $$\mu_{xy} = 0.69 - 0.5 · 1 = 0.19.$$
Without knowledge of the equation $\mu_{xy} = m_{xy} - m_x\cdot m_y$ one would have had to first determine the means $m_x$ and $m_y$ in the first run, and then determine the covariance $\mu_{xy}$ as the expected value of the product of the zero mean variables in a second run.
Correlation coefficient
With statistical independence of the two components $x$ and $y$ the covariance $\mu_{xy} \equiv 0$. This case has already been considered in $\text{Example 2}$ in the section "PDF for statistically independent components".
- But the result $\mu_{xy} = 0$ is also possible for statistically dependent components $x$ and $y$ namely when they are uncorrelated, i.e. "linearly independent".
- The statistical dependence is then not of first order, but of higher order, for example corresponding to the equation $y=x^2.$
One speaks of »complete correlation« when the (deterministic) dependence between $x$ and $y$ is expressed by the equation $y = K · x$. Then the covariance is given by:
- $\mu_{xy} = σ_x · σ_y$ with positive $K$ value,
- $\mu_{xy} = - σ_x · σ_y$ with negative $K$ value.
Therefore, instead of the "covariance" one often uses the so-called "correlation coefficient" as descriptive quantity.
$\text{Definition:}$ The »correlation coefficient« is the quotient of the covariance $\mu_{xy}$ and the product of the standard deviations $σ_x$ and $σ_y$ of the two components:
- $$\rho_{xy}=\frac{\mu_{xy} }{\sigma_x \cdot \sigma_y}.$$
The correlation coefficient $\rho_{xy}$ has the following properties:
- Because of normalization, $-1 \le ρ_{xy} ≤ +1$ always holds.
- If the two random variables $x$ and $y$ are uncorrelated, then $ρ_{xy} = 0$.
- For strict linear dependence between $x$ and $y$ ⇒ $ρ_{xy}= ±1$ ⇒ complete correlation.
- A positive correlation coefficient means that when $x$ is larger, on statistical average, $y$ is also larger than when $x$ is smaller.
- In contrast, a negative correlation coefficient expresses that $y$ becomes smaller on average as $x$ increases.
$\text{Example 5:}$ The following conditions apply:
- The considered components $x$ and $y$ each have a Gaussian PDF.
- The two standard deviations are different $(σ_y < σ_x)$.
- The correlation coefficient is $ρ_{xy} = 0.8$.
Unlike $\text{Example 2}$ with statistically independent components ⇒ $ρ_{xy} = 0$ $($even though $σ_y < σ_x)$ one recognizes that here
- with larger $x$–value, on statistical average, $y$ is also larger
- than with a smaller $x$–value.
Regression line
$\text{Definition:}$ The »regression line« – sometimes called "correlation line" – is the straight line $y = K(x)$ in the $(x, y)$–plane through the "midpoint" $(m_x, m_y)$.
The regression line has the following properties:
- The mean square deviation from this straight line - viewed in $y$–direction and averaged over all $N$ points - is minimal:
- $$\overline{\varepsilon_y^{\rm 2} }=\frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}\; \;\big [y_\nu - K(x_{\nu})\big ]^{\rm 2}={\rm minimum}.$$
- The regression line can be interpreted as a kind of "statistical symmetry axis". The equation of the straight line is:
- $$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x - m_x)+m_y.$$
- The angle taken by the regression line to the $x$–axis is:
- $$\theta_{y\hspace{0.05cm}\rightarrow \hspace{0.05cm}x}={\rm arctan}\ (\frac{\sigma_{y} }{\sigma_{x} }\cdot \rho_{xy}).$$
By this nomenclature it should be made clear that we are dealing here with the regression of $y$ on $x$.
- The regression in the opposite direction – that is, from $x$ to $y$ – on the other hand, means the minimization of the mean square deviation in $x$–direction.
- The (German language) applet "Korrelation und Regressionsgerade" ⇒ "Correlation Coefficient and Regression Line" illustrates
that in general $($if $σ_y \ne σ_x)$ for the regression of $x$ on $y$ will result in a different angle and thus a different regression line:
- $$\theta_{x\hspace{0.05cm}\rightarrow \hspace{0.05cm} y}={\rm arctan}\ (\frac{\sigma_{x}}{\sigma_{y}}\cdot \rho_{xy}).$$
Exercises for the chapter
Exercise 4.1: Triangular (x, y) Area
Exercise 4.1Z: Appointment to Breakfast
Exercise 4.2: Triangle Area again
Exercise 4.2Z: Correlation between "x" and "e to the Power of x"
Exercise 4.3: Algebraic and Modulo Sum
Exercise 4.3Z: Dirac-shaped 2D PDF