Difference between revisions of "Mobile Communications/The GWSSUS Channel Model"
| (60 intermediate revisions by 4 users not shown) | |||
| Line 6: | Line 6: | ||
}} | }} | ||
| − | == Generalized system functions of time variant systems == | + | == Generalized system functions of time variant-systems == |
<br> | <br> | ||
Linear time-invariant systems $\rm (LTI)$ can be completely described with only two system functions, | Linear time-invariant systems $\rm (LTI)$ can be completely described with only two system functions, | ||
*the transfer function $H(f)$ and | *the transfer function $H(f)$ and | ||
| − | *the impulse response $h(t)$ & | + | *the impulse response $h(t)$ ⇒ after renaming $h(\tau)$. |
| Line 22: | Line 22: | ||
*Either a $\boldsymbol{\rm Z}$ $($because of German $\rm Z\hspace{-0.05cm}$eit ⇒ time $t)$ or a $\boldsymbol{\rm D}$ $($Doppler frequency $f_{\rm D})$ is possible as the second subindex. | *Either a $\boldsymbol{\rm Z}$ $($because of German $\rm Z\hspace{-0.05cm}$eit ⇒ time $t)$ or a $\boldsymbol{\rm D}$ $($Doppler frequency $f_{\rm D})$ is possible as the second subindex. | ||
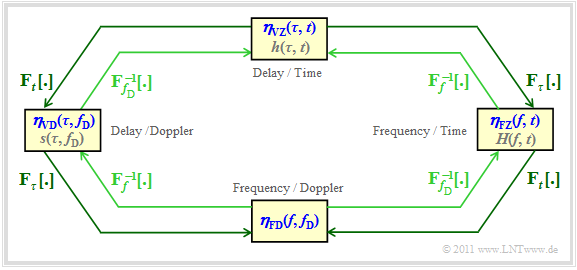
| − | [[File: | + | [[File:EN_Mob_T_2_3_S1_neu.png|right|frame|Relation between the four system functions|class=fit]] |
| − | + | <br>Since, in contrast to line-based transmission, the system functions of mobile communications cannot be described deterministically, but are statistical variables, the corresponding correlation functions must be considered later on. | |
| + | |||
| + | In the following, we will refer to these as $\boldsymbol{\varphi}_{12}$, and use the same indices as for the system functions $\boldsymbol{\eta}_{12}$.<br> | ||
*These formalized designations are inscribed in the graphic in blue letters. | *These formalized designations are inscribed in the graphic in blue letters. | ||
| − | *Additionally, the designations used in other chapters or literature are given ( | + | *Additionally, the designations used in other chapters or literature are given (gray letters). In the other chapters these are also partly used. |
<br clear=all> | <br clear=all> | ||
| − | $(1)$ At the top you can see the '''time variant impulse response''' ${\eta}_{\rm VZ}(\tau,\hspace{0.05cm} t) \equiv h(\tau,\hspace{0.05cm} t)$ in the | + | ${\rm (1)}$ At the top you can see the »'''time-variant impulse response'''« ${\eta}_{\rm VZ}(\tau,\hspace{0.05cm} t) \equiv h(\tau,\hspace{0.05cm} t)$ in the "delay–time range". The associated auto-correlation function $\rm (ACF)$ is |
| − | ::<math>\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \big[ \eta_{\rm VZ}(\tau_1,\hspace{0.05cm} t_1) \cdot | + | :::<math>\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \big[ \eta_{\rm VZ}(\tau_1,\hspace{0.05cm} t_1) \cdot |
\eta_{\rm VZ}^{\star}(\tau_2, t_2) \big]\hspace{0.05cm}. </math> | \eta_{\rm VZ}^{\star}(\tau_2, t_2) \big]\hspace{0.05cm}. </math> | ||
| − | + | ${\rm (2)}$ For the "frequency–time representation" you get the »'''time-variant transfer function'''« ${\eta}_{\rm FZ}(f,\hspace{0.05cm} t) \equiv H(f,\hspace{0.05cm} t)$. | |
| − | ::<math>\eta_{\rm FZ}(f, \hspace{0.05cm} t) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau,\hspace{0.05cm} t) \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau}\hspace{0.15cm}{\rm d}\tau | + | <br> The Fourier transform with respect to $\tau$ is represented in the graph by ${\rm F}_\tau\hspace{0.05cm}[ \cdot ]$ . The Fourier integral is written out in full: |
| + | :::<math>\eta_{\rm FZ}(f, \hspace{0.05cm} t) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau,\hspace{0.05cm} t) \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau}\hspace{0.15cm}{\rm d}\tau | ||
\hspace{0.05cm}, \hspace{0.3cm} \text{kurz:} \hspace{0.2cm} \eta_{\rm FZ}(f, t) | \hspace{0.05cm}, \hspace{0.3cm} \text{kurz:} \hspace{0.2cm} \eta_{\rm FZ}(f, t) | ||
\hspace{0.2cm} \stackrel{f, \hspace{0.05cm} \tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t) | \hspace{0.2cm} \stackrel{f, \hspace{0.05cm} \tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | The ACF of this time variant transfer function is | + | :The ACF of this time-variant transfer function is generally: |
| − | ::<math>\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) = {\rm E} \big [ \eta_{\rm FZ}(f_1, t_1) \cdot | + | :::<math>\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) = {\rm E} \big [ \eta_{\rm FZ}(f_1, t_1) \cdot |
\eta_{\rm FZ}^{\star}(f_2, t_2) \big ]\hspace{0.05cm}.</math> | \eta_{\rm FZ}^{\star}(f_2, t_2) \big ]\hspace{0.05cm}.</math> | ||
| − | + | ${\rm (3)}$ The »'''Scatter–Function'''« ${\eta}_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D}) \equiv s(\tau,\hspace{0.05cm} f_{\rm D})$ corresponding to the left block describes the mobile communications channel in the "delay–Doppler area". | |
| + | <br> $f_{\rm D}$ describes the [[Mobile_Communications/Statistical_Bindings_within_the_Rayleigh_Process#Doppler_frequency_and_its_distribution|$\text{Doppler frequency}$]]. The scatter function results from ${\eta}_{\rm VZ}(\tau,\hspace{0.05cm} t)$ through Fourier transformation with respect to the second parameter $t$: | ||
| − | ::<math> \eta_{\rm VD}(\tau, f_{\rm D}) | + | :::<math> \eta_{\rm VD}(\tau, f_{\rm D}) |
\hspace{0.2cm} \stackrel{f_{\rm D}, \hspace{0.05cm}t}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t)\hspace{0.3cm} | \hspace{0.2cm} \stackrel{f_{\rm D}, \hspace{0.05cm}t}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t)\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} \varphi_{\rm VD}(\tau_1, f_{\rm D_1}, \tau_2, f_{\rm D_2}) = {\rm E} \left [ \eta_{\rm VD}(\tau_1, f_{\rm D_1}) \cdot | \Rightarrow \hspace{0.3cm} \varphi_{\rm VD}(\tau_1, f_{\rm D_1}, \tau_2, f_{\rm D_2}) = {\rm E} \left [ \eta_{\rm VD}(\tau_1, f_{\rm D_1}) \cdot | ||
| Line 52: | Line 56: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | ${\rm (4)}$ Finally, we consider the so-called »'''frequency-variant transfer function'''« $\eta_{\rm FD}(f, f_{\rm D})$, i.e. the "frequency–Doppler representation". | |
| + | <br> According to the graph, this can be reached in two ways: | ||
| + | |||
| + | ::$$\eta_{\rm FD}(f, f_{\rm D}) | ||
| + | \hspace{0.2cm} \stackrel{f_{\rm D}, \hspace{0.05cm}t}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm FZ}(f, t)\hspace{0.05cm},\hspace{0.5cm}\eta_{\rm FD}(f, f_{\rm D}) | ||
| + | \hspace{0.2cm} \stackrel{f, \hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VD}(\tau, f_{\rm D})\hspace{0.05cm}.$$ | ||
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Notes:}$ | |
| + | *The specified Fourier correlations between the system functions in the graph are illustrated by the outer, dark green arrows and are marked with ${\rm F}_p\hspace{0.05cm}[\hspace{0.05cm} \cdot \hspace{0.05cm}]$ , <br>the index $p$ indicates to which parameter $\tau$, $f$, $t$ or $f_{\rm D}$ does the Fourier transformation refer. | ||
| − | + | *The inner (lighter) arrows indicate the links via the [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_second_Fourier_integral|$\text{inverse Fourier transform}$]]. For this we use the notation ${ {\rm F}_p}^{-1}\hspace{0.05cm}[ \hspace{0.05cm} \cdot \hspace{0.05cm} ]$. | |
| − | |||
| − | + | *The applet [[Applets:Impulses and Spectra|"Impulses and Spectra"]] illustrates the connection between the time and frequency domain, which can be described by formulas using Fourier transformation and Fourier inverse transformation.}} | |
| − | |||
| − | |||
| − | |||
| − | *The applet [[Applets:Impulses and Spectra]] illustrates the connection between the time and frequency domain, which can be described by formulas using Fourier transformation and Fourier inverse transformation.}} | ||
| Line 71: | Line 76: | ||
The general relationship between the four system functions is very complicated due to non-stationary effects. | The general relationship between the four system functions is very complicated due to non-stationary effects. | ||
| − | [[File: | + | [[File:EN_Mob_T_2_3_S2_v2.png|right|frame|Connections between the description functions of the GWSSUS model|class=fit]] |
Compared to the general model, some limitations have to be made in order to arrive at a suitable model for the mobile communications channel from which relevant statements for practical applications can be derived.<br> | Compared to the general model, some limitations have to be made in order to arrive at a suitable model for the mobile communications channel from which relevant statements for practical applications can be derived.<br> | ||
| Line 77: | Line 82: | ||
*The random process of the channel impulse response $h(\tau,\hspace{0.1cm} t) = {\eta}_{\rm VZ}(\tau,\hspace{0.1cm} t)$ is generally assumed to be complex (i.e., description in the equivalent low-pass range), Gaussian $($identifier $\rm G)$ and zero-mean (Rayleigh, not Rice, that means, no line of sight) .<br> | *The random process of the channel impulse response $h(\tau,\hspace{0.1cm} t) = {\eta}_{\rm VZ}(\tau,\hspace{0.1cm} t)$ is generally assumed to be complex (i.e., description in the equivalent low-pass range), Gaussian $($identifier $\rm G)$ and zero-mean (Rayleigh, not Rice, that means, no line of sight) .<br> | ||
| − | *The random process is weakly stationary ⇒ its characteristics change only slightly with time, and the ACF $ {\varphi}_{\rm VZ}(\tau_1,\hspace{0.05cm} t_1,\hspace{0.05cm}\tau_2,\hspace{0.05cm} t_2)$ of the time variant impulse response does not depend on the absolute times $t_1$ and $t_2$ but only on the time difference $\Delta t = t_2 - t_1$. This is indicated by the identifier $\rm WSS$ ⇒ $\rm W$ide $\rm S$ense $\rm S$tationary.<br> | + | *The random process is weakly stationary ⇒ its characteristics change only slightly with time, and the ACF $ {\varphi}_{\rm VZ}(\tau_1,\hspace{0.05cm} t_1,\hspace{0.05cm}\tau_2,\hspace{0.05cm} t_2)$ of the time-variant impulse response does not depend on the absolute times $t_1$ and $t_2$ but only on the time difference $\Delta t = t_2 - t_1$. This is indicated by the identifier $\rm WSS$ ⇒ $\rm W$ide $\rm S$ense $\rm S$tationary.<br> |
*The individual echoes due to multipath propagation are uncorrelated, which is expressed by the identifier $\rm US$ ⇒ $\rm U$ncorrelated $\rm S$cattering</i>. | *The individual echoes due to multipath propagation are uncorrelated, which is expressed by the identifier $\rm US$ ⇒ $\rm U$ncorrelated $\rm S$cattering</i>. | ||
<br clear=all> | <br clear=all> | ||
| − | The mobile communications channel can be described in full according to this graph. The individual power | + | The mobile communications channel can be described in full according to this graph. The individual power-spectral densities (labeled blue) and the correlation function (labeled red) is explained in detail in the following sections.<br> |
| − | == | + | == Auto-correlation function of the time-variant impulse response== |
<br> | <br> | ||
| − | We now consider the [[Theory_of_Stochastic_Signals/ | + | We now consider the [[Theory_of_Stochastic_Signals/Auto-Correlation_Function_(ACF)|$\text{auto-correlation function}$]] $\rm (ACF)$ of the time-variant impulse response ⇒ $h(\tau,\hspace{0.1cm} t) = {\eta}_{\rm VZ}(\tau,\hspace{0.1cm} t)$ more closely. It shows: |
| − | *Based on the $\rm WSS$ property, the | + | *Based on the $\rm WSS$ property, the auto-correlation function can be written with $\Delta t = t_2 - t_1$ : |
::<math>\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = \varphi_{\rm VZ}(\tau_1, \tau_2, \Delta t)\hspace{0.05cm}.</math> | ::<math>\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = \varphi_{\rm VZ}(\tau_1, \tau_2, \Delta t)\hspace{0.05cm}.</math> | ||
| − | *Since the echoes were assumed to be independent of each other $\rm (US$ property$)$, the impulse response can be assumed to be uncorrelated with respect to the delays $\tau_1$ and $\tau_2$ Then: | + | *Since the echoes were assumed to be independent of each other $\rm (US$ property$)$, the impulse response can be assumed to be uncorrelated with respect to the delays $\tau_1$ and $\tau_2$. Then: |
::<math>\varphi_{\rm VZ}(\tau_1, \tau_2, \Delta t) = 0 \hspace{0.35cm}{\rm f\ddot{u}r}\hspace{0.35cm} \tau_1 \ne \tau_2\hspace{0.05cm}. </math> | ::<math>\varphi_{\rm VZ}(\tau_1, \tau_2, \Delta t) = 0 \hspace{0.35cm}{\rm f\ddot{u}r}\hspace{0.35cm} \tau_1 \ne \tau_2\hspace{0.05cm}. </math> | ||
| − | *If one now replaces $\tau_1$ with $\tau$ and $\tau_2$ with $\tau + \Delta \tau$, this | + | *If one now replaces $\tau_1$ with $\tau$ and $\tau_2$ with $\tau + \Delta \tau$, this auto-correlation function can be represented in the following way: |
::<math>\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}. </math> | ::<math>\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}. </math> | ||
| − | *Because of the convolution property of the Dirac function, the ACF for $\tau_1 \ne \tau_2$ ⇒ $\Delta \tau \ne 0$ disappears. | + | *Because of the convolution property of the Dirac delta function, the ACF for $\tau_1 \ne \tau_2$ ⇒ $\Delta \tau \ne 0$ disappears. |
| − | *$ {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.1cm}$ is the | + | *$ {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.1cm}$ is the »'''delay–time's cross power-spectral density'''«, which depends on the delay $\tau \ (= \tau_1 =\tau_2)$ and on the time difference $\Delta t = t_2 - t_1$ . |
| − | + | <br> | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Please note:}$ | $\text{Please note:}$ | ||
| − | *With this approach, | + | *With this approach, the auto-correlation function $\varphi_{\rm VZ}(\Delta \tau, \Delta t)$ and the power-spectral density ${\it \Phi}_{\rm VZ}(\tau, \Delta t) $ are not connected via the Fourier transform as usual, but are linked via a Dirac delta function: |
::<math>\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}. </math> | ::<math>\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}. </math> | ||
| − | *Not all symmetry properties that follow from the [[Theory_of_Stochastic_Signals/ | + | *Not all symmetry properties that follow from the [[Theory_of_Stochastic_Signals/Power_Density_Spectrum_(PDS)#Wiener-Khintchine_Theorem| $\text{Wiener–Khintchine theorem}$]] are thus given here. In particular it is quite possible and even very likely that such a power-spectral density is an odd function.}}<br> |
| − | In the overview | + | In the overview in the last section, the »'''delay–time's cross power-spectral density'''« ${\it \Phi}_{\rm VZ}(\tau, \Delta t) $ can be seen in the top middle. |
| − | *Since $\eta_{\rm VZ}(\tau, t) $ | + | *Since $\eta_{\rm VZ}(\tau, t) $, like any [[Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain#Impulse_response|$\text{impulse response}$]], has the unit $\rm [1/s]$ , the auto-correlation function has the unit $\rm [1/s^2]$: |
::<math>\varphi_{\rm VZ}(\Delta \tau, \Delta t) = {\rm E} \left [ \eta_{\rm VZ}(\tau, t) \cdot | ::<math>\varphi_{\rm VZ}(\Delta \tau, \Delta t) = {\rm E} \left [ \eta_{\rm VZ}(\tau, t) \cdot | ||
\eta_{\rm VZ}^{\star}(\tau + \Delta \tau, t + \Delta t) \right ].</math> | \eta_{\rm VZ}^{\star}(\tau + \Delta \tau, t + \Delta t) \right ].</math> | ||
| − | *But since the Dirac function with the time argument $\delta(\Delta \tau)$ also has the unit $\rm [1/s]$ the delay–time's cross power density | + | *But since the Dirac delta function with the time argument $\delta(\Delta \tau)$ also has the unit $\rm [1/s]$ the delay–time's cross power-spectral density ${\it \Phi}_{\rm VZ}(\tau, \Delta t) $ also has the unit $\rm [1/s]$: |
::<math>\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}.</math> | ::<math>\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}.</math> | ||
| − | == Power spectral density of the time variant impulse response== | + | == Power-spectral density of the time-variant impulse response== |
<br> | <br> | ||
| − | [[File:P ID2170 Mob T 2 3 S3a v2.png|right|frame|Delay power density | + | [[File:P ID2170 Mob T 2 3 S3a v2.png|right|frame|Delay's power-spectral density |class=fit]] |
| − | One obtains the '''delay's power density | + | One obtains the »'''delay's power-spectral density'''« ${\it \Phi}_{\rm V}(\Delta \tau)$ by setting the second parameter of ${\it \Phi}_{\rm VZ}(\Delta \tau, \Delta t)$ to $\Delta t = 0$ . The graphic on the right shows an exemplary curve.<br> |
| − | The delay's power density | + | The delay's power-spectral density is a central quantity for the description of the mobile communications channel. This has the following characteristics: |
*${\it \Phi}_{\rm V}(\Delta \tau_0)$ is a measure for the "power" of those signal components which are delayed by $\tau_0$ . For this purpose, an implicit averaging over all Doppler frequencies $(f_{\rm D})$ is carried out.<br> | *${\it \Phi}_{\rm V}(\Delta \tau_0)$ is a measure for the "power" of those signal components which are delayed by $\tau_0$ . For this purpose, an implicit averaging over all Doppler frequencies $(f_{\rm D})$ is carried out.<br> | ||
| − | *The delay's power density | + | *The delay's power-spectral density ${\it \Phi}_{\rm V}(\Delta \tau)$ has, like ${\it \Phi}_{\rm VZ}(\Delta \tau, \Delta t)$ , the unit $\rm [1/s]$. It characterizes the power distribution over all possible delays $\tau$.<br> |
| − | *In the | + | *In the graphic, the power $ P_0 \approx {\it \Phi}_{\rm V}(\Delta \tau_0)\cdot \Delta \tau$ of those signal components that arrive at the receiver via any path with a delay between $\tau_0 \pm \Delta \tau/2$. <br> |
| − | *Normalizing the power density | + | *Normalizing the power-spectral density ${\it \Phi}_{\rm V}(\Delta \tau)$ in such a way that the area is $1$ results in the probability density function $\rm (PDF)$ of the delay time: |
::<math>{\rm PDF}_{\rm V}(\tau) = \frac{{\it \Phi}_{\rm V}(\tau)}{\int_{0 }^{\infty}{\it \Phi}_{\rm V}(\tau)\hspace{0.15cm}{\rm d}\tau} \hspace{0.05cm}.</math> | ::<math>{\rm PDF}_{\rm V}(\tau) = \frac{{\it \Phi}_{\rm V}(\tau)}{\int_{0 }^{\infty}{\it \Phi}_{\rm V}(\tau)\hspace{0.15cm}{\rm d}\tau} \hspace{0.05cm}.</math> | ||
| − | ''Note on nomenclature'': | + | '''Note on nomenclature''': |
| − | *In the book "Stochastic Signal Theory" we would have denoted this [[Theory_of_Stochastic_Signals/ | + | *In the book "Stochastic Signal Theory" we would have denoted this [[Theory_of_Stochastic_Signals/Probability_Density_Function_(PDF)#Definition_of_the_probability_density_function|$\text{probability density function}$]] with $f_\tau(\tau)$. |
| − | *To make the | + | *To make the relation between ${\it \Phi}_{\rm V}(\Delta \tau)$ and the PDF clear and to avoid confusion with the frequency $f$ we use the nomenclature given here.<br> |
| Line 147: | Line 152: | ||
<br> | <br> | ||
| − | In the 1990s, the European Union founded the working group COST 207 with the aim to provide standardized channel models for cellular mobile communications. where "COST" stands for | + | In the 1990s, the European Union founded the working group COST 207 with the aim to provide standardized channel models for cellular mobile communications. where "COST" stands for "European Cooperation in Science and Technology".<br> |
| − | In this international committee profiles for the delay time $\tau$ have been developed, based on measurements and valid for different application scenarios. In the following, four different delay's power spectral densities are given, where the normalization factor ${\it \Phi}_0 = {\it \Phi}_{\rm V}(\tau = 0)$ is always used. The graph shows the | + | In this international committee profiles for the delay time $\tau$ have been developed, based on measurements and valid for different application scenarios. In the following, four different delay's power-spectral densities are given, where the normalization factor ${\it \Phi}_0 = {\it \Phi}_{\rm V}(\tau = 0)$ is always used. The graph shows the PSDs of these profiles in logarithmic representation: |
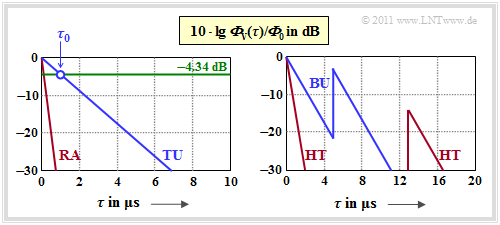
| − | [[File:P ID2175 Mob T 2 3 S4a v1.png|right|frame|Delay power | + | [[File:P ID2175 Mob T 2 3 S4a v1.png|right|frame|Delay's power-spectral densities according to COST|class=fit]] |
| − | '''(1)''' profile $\rm RA$ ( | + | '''(1)''' profile $\rm RA$ ("Rural Area"): |
::<math>{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} | ::<math>{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} | ||
| − | \hspace{0.3cm} | + | \hspace{0.3cm}\text{for}\hspace{0.2cm} 0 < \tau < 0.7\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 0.109\,{\rm µ s}\hspace{0.05cm}.</math> |
| − | '''(2)''' profile $\rm TU$ ( | + | '''(2)''' profile $\rm TU$ ("Typical Urban") ⇒ cities and suburbs: |
::<math>{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} | ::<math>{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} | ||
| − | \hspace{0.3cm} | + | \hspace{0.3cm}\text{for}\hspace{0.2cm} 0 < \tau < 7\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s}\hspace{0.05cm}.</math> |
| − | '''(3)''' profile $\rm BU$ ( | + | '''(3)''' profile $\rm BU$ ("Bad Urban") ⇒ unfavourable conditions in cities: |
::<math>{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} | ::<math>{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} | ||
= \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0}\\ | = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0}\\ | ||
0.5 \cdot {\rm e}^{ (5\,{\rm µ s}-\tau) / \tau_0} \end{array} \right.\quad | 0.5 \cdot {\rm e}^{ (5\,{\rm µ s}-\tau) / \tau_0} \end{array} \right.\quad | ||
| − | \begin{array}{*{1}l} \hspace{0.1cm} {\rm | + | \begin{array}{*{1}l} \hspace{0.1cm} {\rm for}\hspace{0.3cm} 0 < \tau < 5\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s}\hspace{0.05cm}, |
| − | \\ \hspace{0.1cm} {\rm | + | \\ \hspace{0.1cm} {\rm for}\hspace{0.3cm} 5\,{\rm µ s} < \tau < 10\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}. \\ \end{array}</math> |
| − | '''(4)''' profile $\rm HT$ ( | + | '''(4)''' profile $\rm HT$ ("Hilly Terrain") ⇒ hilly and mountainous regions: |
::<math>{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} | ::<math>{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} | ||
= \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0}\\ | = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0}\\ | ||
0.04 \cdot {\rm e}^{ (15\,{\rm µ s}-\tau) / \tau_0} \end{array} \right.\quad | 0.04 \cdot {\rm e}^{ (15\,{\rm µ s}-\tau) / \tau_0} \end{array} \right.\quad | ||
| − | \begin{array}{*{1}l} \hspace{-0.25cm} {\rm | + | \begin{array}{*{1}l} \hspace{-0.25cm} {\rm for}\hspace{0.3cm} 0 < \tau < 2\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 0.286\,{\rm µ s}\hspace{0.05cm}, |
\\ \hspace{-0.25cm} {\rm for}\hspace{0.3cm} 15\,{\rm µ s} < \tau < 20\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}. \\ \end{array}</math> | \\ \hspace{-0.25cm} {\rm for}\hspace{0.3cm} 15\,{\rm µ s} < \tau < 20\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}. \\ \end{array}</math> | ||
| − | One can | + | One can see from the graphics: |
*The exponential functions in linear representation now become straight lines.<br> | *The exponential functions in linear representation now become straight lines.<br> | ||
| − | *For logarithmic display, you can read the | + | |
| − | *These four COST | + | *For logarithmic display, you can read the PSD parameter $\tau_0$ for $\rm 10 \cdot lg \ (1/e) = -4.34 \ dB$ as shown in the graph for the $\rm TU$ profile. |
| + | |||
| + | *These four COST profiles are described in the [[Aufgaben:Exercise 2.8: COST Delay Models|"Exercise 2.8"]] in more detail.}} | ||
<br clear =all> | <br clear =all> | ||
| − | == ACF and | + | == ACF and PSD of the frequency-variant transfer function== |
<br> | <br> | ||
| − | The system function $\eta_{\rm FD}(f, f_{\rm D})$ described in the nbsp; [[Mobile_Communications/The_GWSSUS channel model#Generalized system functions_of time variant_systems|overview | + | The system function $\eta_{\rm FD}(f, f_{\rm D})$ described in the [[Mobile_Communications/The_GWSSUS channel model#Generalized system functions_of time variant_systems|"overview in the first section of this chapter"]] is also known as the "Frequency-variant Transfer Function" where the adjective "frequency-variant" refers to the Doppler frequency $f_{\rm D}$. |
| − | The associated ACF is defined as follows: | + | The associated auto-correlation function $\rm (ACF)$ is defined as follows: |
::<math>\varphi_{\rm FD}(f_1, f_{\rm D_1}, f_2, f_{\rm D_2}) = {\rm E} \left [ \eta_{\rm FD}(f_1, f_{\rm D_1}) \cdot | ::<math>\varphi_{\rm FD}(f_1, f_{\rm D_1}, f_2, f_{\rm D_2}) = {\rm E} \left [ \eta_{\rm FD}(f_1, f_{\rm D_1}) \cdot | ||
\eta_{\rm FZ}^{\star}(f_2, f_{\rm D_2}) \right ]\hspace{0.05cm}. </math> | \eta_{\rm FZ}^{\star}(f_2, f_{\rm D_2}) \right ]\hspace{0.05cm}. </math> | ||
| − | By similar considerations as | + | By similar considerations as in the [[Mobile_Communications/The_GWSSUS_Channel_Model#Power_density_spectrum_of_the_time-variant_impulse_response|"previous section"]] this auto-correlation function can be represented under GWSSUS conditions as follows |
::<math>\varphi_{\rm FD}(\Delta f, \Delta f_{\rm D}) = \delta(\Delta f_{\rm D}) \cdot {\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) \hspace{0.05cm}.</math> | ::<math>\varphi_{\rm FD}(\Delta f, \Delta f_{\rm D}) = \delta(\Delta f_{\rm D}) \cdot {\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) \hspace{0.05cm}.</math> | ||
The following applies: | The following applies: | ||
| − | *${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ is the so-called | + | *${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ is the so-called »'''frequency–Doppler's cross power-spectral density'''«, which is highlighted in the graphic by a yellow background.<br> |
| − | *The first argument $\Delta f = f_2 - f_1$ takes into account that ACF and | + | *The first argument $\Delta f = f_2 - f_1$ takes into account that ACF and PSD depend only on the frequency difference due to the "stationarity" . |
| − | *The factor $\delta (\Delta f_{\rm D})$ with $\Delta f_{\rm D} = f_{\rm D_2} - f_{\rm D_1}$ expresses the | + | |
| + | *The factor $\delta (\Delta f_{\rm D})$ with $\Delta f_{\rm D} = f_{\rm D_2} - f_{\rm D_1}$ expresses the "uncorrelation of the PSD" with respect to the Doppler shift.<br> | ||
| − | *You get from ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ to '''Doppler's | + | *You get from ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ to »'''Doppler's power-spectral density'''« ${\it \Phi}_{\rm D}(f_{\rm D})$ if you set $\Delta f= 0$. |
| − | *The Doppler's power density | + | |
| − | + | *The Doppler's power-spectral density ${\it \Phi}_{\rm D}(f_{\rm D})$ indicates the power with which individual Doppler frequencies occur.<br> | |
| − | |||
| − | |||
| − | |||
| + | *The probability density function $\rm (PDF)$ of the Doppler frequency is obtained from ${\it \Phi}_{\rm D}(f_{\rm D})$ by suitable normalization. The PDF has like ${\it \Phi}_{\rm D}(f_{\rm D})$ the unit $\rm [1/Hz]$. | ||
| + | [[File:P ID2173 Mob T 2 3 S5 v1.png|right|frame|To calculate the Doppler's power-spectral density|class=fit]] | ||
::<math>{\rm PDF}_{\rm D}(f_{\rm D}) = \frac{{\it \Phi}_{\rm D}(f_{\rm D})}{\int_{-\infty }^{+\infty}{\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.15cm}{\rm d}f_{\rm D}} \hspace{0.05cm}.</math> | ::<math>{\rm PDF}_{\rm D}(f_{\rm D}) = \frac{{\it \Phi}_{\rm D}(f_{\rm D})}{\int_{-\infty }^{+\infty}{\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.15cm}{\rm d}f_{\rm D}} \hspace{0.05cm}.</math> | ||
| − | *Often, for example for a vertical monopulse antenna in an isotropically scattered field, the ${\it \Phi}_{\rm D}(f_{\rm D})$ given | + | *Often, for example for a vertical monopulse antenna in an isotropically scattered field, the ${\it \Phi}_{\rm D}(f_{\rm D})$ is given by the [[Mobile_Communications/Statistical_Bindings_within_the_Rayleigh_Process#Doppler_frequency_and_its_distribution| $\text{Jakes spectrum}$]] .<br> |
| − | The | + | The frequency–Doppler's cross power-spectral density ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ is highlighted in yellow. The Fourier connections to the neighboring GWSSUS system description functions ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$ and ${\it \varphi}_{\rm FZ}(\Delta f, \Delta t)$ are also marked. |
| − | |||
| − | + | We refer here to the interactive applet [[Applets:The_Doppler_Effect|"The Doppler Effect"]]. | |
<br clear=all> | <br clear=all> | ||
| − | == ACF and | + | == ACF and PSD of the delay-Doppler function == |
<br> | <br> | ||
| − | The system function shown in the [[Mobile_Communications/The_GWSSUS channel model#Generalized_system functions_of time variant_systems| | + | The system function shown in the [[Mobile_Communications/The_GWSSUS channel model#Generalized_system functions_of time variant_systems|"overview in the first section of this chapter"]] on the left hand side was named $\eta_{\rm VD}(\tau, f_{\rm D})$ . |
| + | |||
| + | The auto-correlation function $\rm (ACF)$ of this delay–Doppler function can be written with $\Delta \tau = \tau_2 - \tau_1$ and $\Delta f_{\rm D} = f_{\rm D2} - f_{\rm D1}$ taking into account the GWSSUS properties with $\Delta \tau = \tau_2 - \tau_1$ and $\Delta f_{\rm D} = f_{\rm D2} - f_{\rm D1}$ as follows | ||
::<math>\varphi_{\rm VD}(\tau_1, f_{\rm D_1}, \tau_2, f_{\rm D_2}) = \varphi_{\rm VD}(\Delta \tau, \Delta f_{\rm D}) = | ::<math>\varphi_{\rm VD}(\tau_1, f_{\rm D_1}, \tau_2, f_{\rm D_2}) = \varphi_{\rm VD}(\Delta \tau, \Delta f_{\rm D}) = | ||
| Line 225: | Line 233: | ||
It should be noted about this equation: | It should be noted about this equation: | ||
| − | *The first Dirac function $\delta (\ | + | *The first Dirac delta function $\delta (\Delta \tau)$ takes into account that the delays are uncorrelated ("Uncorrelated Scattering"). |
| − | *The second Dirac function $\delta (\Delta f_{\rm D})$ follows from the stationarity (" | + | |
| + | *The second Dirac delta function $\delta (\Delta f_{\rm D})$ follows from the stationarity ("Wide Sense Stationary").<br> | ||
| − | *The delay–Doppler's | + | *The delay–Doppler's power-spectral density ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$ , also called »'''Scatter Function'''« can be calculated from ${\it \Phi}_{\rm VZ}(\tau, \Delta t)$ or ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ as follows: |
::<math>{\it \Phi}_{\rm VD}(\tau, f_{\rm D}) ={\rm F}_{\Delta t} \big [ {\it \Phi}_{\rm VZ}(\tau, \Delta t) \big ] | ::<math>{\it \Phi}_{\rm VD}(\tau, f_{\rm D}) ={\rm F}_{\Delta t} \big [ {\it \Phi}_{\rm VZ}(\tau, \Delta t) \big ] | ||
| Line 235: | Line 244: | ||
= \int_{-\infty}^{+\infty} {\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) \cdot {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \tau \hspace{0.05cm}\cdot \hspace{0.05cm} \Delta f}\hspace{0.15cm}{\rm d}\Delta f \hspace{0.05cm}. </math> | = \int_{-\infty}^{+\infty} {\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) \cdot {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \tau \hspace{0.05cm}\cdot \hspace{0.05cm} \Delta f}\hspace{0.15cm}{\rm d}\Delta f \hspace{0.05cm}. </math> | ||
| − | *Both the system function $\eta_{\rm VD}(\tau, f_{\rm D})$ and the derived functions $\varphi _{\rm VD}(\ | + | *Both, the system function $\eta_{\rm VD}(\tau, f_{\rm D})$ and the derived functions $\varphi _{\rm VD}(\Delta \tau, \Delta f_{\rm D})$ and ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$, are dimensionless. For more information on this, see the specification for [[Aufgaben:Exercise 2.6: Dimensions in GWSSUS|"Exercise 2.6"]]. |
| − | *Furthermore, if the GWSSUS requirements are met, the scatter function is equal to the product of the delay's and Doppler's | + | *Furthermore, if the GWSSUS requirements are met, the scatter function is equal to the product of the delay's and Doppler's PSDs: |
::<math>{\it \Phi}_{\rm VD}(\tau, f_{\rm D}) = {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.05cm}.</math> | ::<math>{\it \Phi}_{\rm VD}(\tau, f_{\rm D}) = {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.05cm}.</math> | ||
| − | [[File:P ID2171 Mob T 2 3 S6 v1.png|right|frame|One-dimensional description functions of the GWSSUS model | + | [[File:P ID2171 Mob T 2 3 S6 v1.png|right|frame|One-dimensional description functions of the GWSSUS model ]] |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Conclusion:}$ | + | $\text{Conclusion:}$ |
| − | It should be noted | + | The figure summarizes the results of this chapter so far. It should be noted: |
| − | '''(1)''' The influence of the delay time $\tau$ and the Doppler frequency $f_{\rm D}$ can be separated | + | '''(1)''' The influence of the delay time $\tau$ and the Doppler frequency $f_{\rm D}$ can be separated |
| − | *the blue power density | + | *into the blue power-spectral density ${\it \Phi}_{\rm V}(\tau)$ |
| − | *the red power density | + | *and the red power-spectral density ${\it \Phi}_{\rm D}(f_{\rm D})$.<br> |
| − | '''(2)''' The | + | '''(2)''' The two–dimensional delay–Doppler's power-spectral density ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$ is equal to the product of these two functions.}} |
<br clear=all> | <br clear=all> | ||
| − | == ACF and | + | == ACF and PSD of the time-variant transfer function == |
<br> | <br> | ||
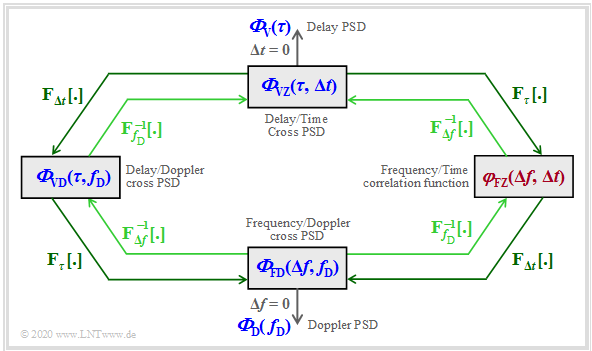
| − | The following diagram shows all the relationships between the individual power spectral densities once again in compact form. | + | The following diagram shows all the relationships between the individual power-spectral densities once again in compact form. |
| − | [[File:P ID2176 Mob T 2 3 S7 v1.png|right|frame|Compact summary of all GWSSUS description | + | [[File:P ID2176 Mob T 2 3 S7 v1.png|right|frame|Compact summary of all GWSSUS description quantities |class=fit]] |
| − | This has already been discussed | + | This has already been discussed in the last sections: |
| − | *the [[Mobile_Communications/ | + | *the [[Mobile_Communications/The_GWSSUS_Channel_Model#Autocorrelation_function_of_the_time-variant_impulse_response|$\text{delay–time's cross-power-spectral density}$]]: |
| − | $${\it \Phi}_{\rm VZ}(\tau, \ | + | :$${\it \Phi}_{\rm VZ}(\tau, \Delta t)\hspace{0.55cm}\Rightarrow \hspace{0.3cm}\text{with} \hspace{0.2cm}\Delta t = 0\text{:} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau),$$ |
| − | *the [[Mobile_Communications/ | + | *the [[Mobile_Communications/The_GWSSUS_Channel_Model#ACF_and_PSD_of_the_frequency-variant_transfer_function|$\text{frequency–Doppler's cross-power-spectral density}$]]: |
:$${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{with} \hspace{0.2cm}\Delta f = 0\text{:} \hspace{0.2cm} {\it \Phi}_{\rm D}( f_{\rm D}),$$ | :$${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{with} \hspace{0.2cm}\Delta f = 0\text{:} \hspace{0.2cm} {\it \Phi}_{\rm D}( f_{\rm D}),$$ | ||
| − | *the [[Mobile_Communications/ | + | *the [[Mobile_Communications/The_GWSSUS_Channel_Model#ACF_and_PSD_of_the_delay-Doppler_function |$\text{delay–Doppler's cross-power-spectral density}$ ]]: |
:$${\it \Phi}_{\rm VD}(\tau, f_{\rm D})= {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.05cm}.$$ | :$${\it \Phi}_{\rm VD}(\tau, f_{\rm D})= {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.05cm}.$$ | ||
| − | + | <br clear=all> | |
| − | + | The »'''frequency–time's correlation function'''« (marked yellow in the adjacent graph) has not yet been considered: | |
| − | The '''frequency–time's | ||
::<math>\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) = {\rm E} \left [ \eta_{\rm FZ}(f_1, t_1) \cdot | ::<math>\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) = {\rm E} \left [ \eta_{\rm FZ}(f_1, t_1) \cdot | ||
\eta_{\rm FZ}^{\star}(f_2, t_2) \right ]\hspace{0.05cm}.</math> | \eta_{\rm FZ}^{\star}(f_2, t_2) \right ]\hspace{0.05cm}.</math> | ||
| − | Considering again the GWSSUS simplifications and the identity $\eta_{\rm FZ}(f, \hspace{0.05cm}t) | + | Considering again the GWSSUS simplifications and the identity $\eta_{\rm FZ}(f, \hspace{0.05cm}t) \equiv H(f, \hspace{0.05cm}t)$, the ACF can be also written with $\Delta f = f_2 - f_1$ and $\Delta t = t_2 - t_1$ as follows: |
::<math>\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\varphi_{\rm FZ}(\Delta f, \Delta t) | ::<math>\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\varphi_{\rm FZ}(\Delta f, \Delta t) | ||
| Line 279: | Line 287: | ||
It should be noted in this respect: | It should be noted in this respect: | ||
| − | *You can see from the name that $\varphi_{\rm FZ}(\Delta f, \Delta t)$ is a correlation function and not a | + | *You already can see from the name that $\varphi_{\rm FZ}(\Delta f, \Delta t)$ is a correlation function and not a PSD like the functions ${\it \Phi}_{\rm VZ}(\tau, \Delta t)$, ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ and ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$. <br> |
| − | *The Fourier | + | *The Fourier relationships with the neighboring functions are: |
::<math>{\it \Phi}_{\rm VZ}(\tau, \Delta t) | ::<math>{\it \Phi}_{\rm VZ}(\tau, \Delta t) | ||
| Line 288: | Line 296: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *If you set the parameters $\Delta t = 0$ or $\Delta f = 0$ in this | + | *If you set the parameters $\Delta t = 0$ or $\Delta f = 0$ in this two–dimensional function, the separate correlation functions for the frequency domain or the time domain result: |
| − | : | + | :$$\varphi_{\rm F}(\Delta f) = \varphi_{\rm FZ}(\Delta f, \Delta t = 0) \hspace{0.05cm},\hspace{0.5cm} |
| − | + | \varphi_{\rm Z}(\Delta t) = \varphi_{\rm FZ}(\Delta f = 0, \Delta t ) \hspace{0.05cm}.$$ | |
| − | *From the | + | *From the graph it is also clear that these correlation functions correspond to the derived power-spectral densities via the Fourier transform: |
::<math>\varphi_{\rm F}(\Delta f) \hspace{0.2cm} {\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau)\hspace{0.05cm}, | ::<math>\varphi_{\rm F}(\Delta f) \hspace{0.2cm} {\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau)\hspace{0.05cm}, | ||
| Line 300: | Line 308: | ||
== Parameters of the GWSSUS model== | == Parameters of the GWSSUS model== | ||
<br> | <br> | ||
| − | According to the results | + | According to the results in the last section, the mobile channel is replaced by |
| − | *the delay | + | *the delay's power-spectral density ${\it \Phi}_{\rm V}(\tau)$ and<br> |
| − | *the Doppler | + | *the Doppler's power-spectral density ${\it \Phi}_{\rm D}(f_{\rm D})$.<br><br> |
| − | By suitable normalization to the respective area $1$ the density functions result with respect to the delay time $\tau$ or the Doppler frequency | + | By suitable normalization to the respective area $1$ the density functions result with respect to the delay time $\tau$ or the Doppler frequency $f_{\rm D}$.<br> |
| − | Characteristic values can be derived from the power spectral densities or the corresponding correlation functions. The most important ones are listed here: | + | Characteristic values can be derived from the power-spectral densities or the corresponding correlation functions. The most important ones are listed here: |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ The '''Multipath Spread''' or '''Time Delay Spread''' & | + | $\text{Definition:}$ The »'''Multipath Spread'''« or »'''Time Delay Spread'''« $T_{\rm V}$ specifies the spread that a Dirac delta experiences through the channel on statistical average. <br>$T_{\rm V}$ is defined as the standard deviation $(\sigma_{\rm V})$ the random variable $\tau$: |
::<math>T_{\rm V} = \sigma_{\rm V} = \sqrt{ {\rm E} \big [ \tau^2 \big ] - m_{\rm V}^2} | ::<math>T_{\rm V} = \sigma_{\rm V} = \sqrt{ {\rm E} \big [ \tau^2 \big ] - m_{\rm V}^2} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *The mean value $m_{\rm V} = {\rm E}\big[\tau \big]$ is | + | *The mean value $m_{\rm V} = {\rm E}\big[\tau \big]$ is an "Average Excess Delay" for all signal components. |
| + | |||
*${\rm E} \big [ \tau^2 \big ] $ is to be calculated as the root mean square value.}} | *${\rm E} \big [ \tau^2 \big ] $ is to be calculated as the root mean square value.}} | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ The '''Coherence Bandwidth''' $B_{\rm K}$ is the $\Delta f$& | + | $\text{Definition:}$ The »'''Coherence Bandwidth'''« $B_{\rm K}$ is the $\Delta f$ value at which the frequency's correlation function has dropped to half of its value for the first time. |
::<math>\vert \varphi_{\rm F}(\Delta f = B_{\rm K})\vert \stackrel {!}{=} {1}/{2} \cdot \vert \varphi_{\rm F}(\Delta f = 0)\vert \hspace{0.05cm}.</math> | ::<math>\vert \varphi_{\rm F}(\Delta f = B_{\rm K})\vert \stackrel {!}{=} {1}/{2} \cdot \vert \varphi_{\rm F}(\Delta f = 0)\vert \hspace{0.05cm}.</math> | ||
| − | *$B_{\rm K}$ is a measure of the minimum frequency difference by which two harmonic oscillations must differ in order to have completely different channel transmission characteristics. | + | *$B_{\rm K}$ is a measure of the minimum frequency difference by which two harmonic oscillations must differ in order to have completely different channel transmission characteristics. |
| − | *If the signal bandwidth is $B_{\rm S} <B_{\rm K}$, then all spectral components are changed in approximately the same way by the channel. <br>This means: Precisely then there is a non-frequency selective fading.}} | + | |
| + | *If the signal bandwidth is $B_{\rm S} <B_{\rm K}$, then all spectral components are changed in approximately the same way by the channel. <br>This means: '''Precisely then there is a non-frequency selective fading'''.}} | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
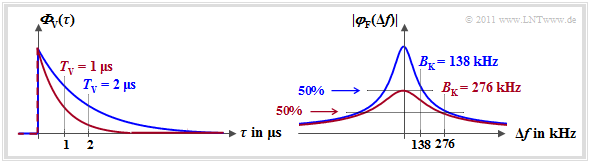
| − | $\text{Example 2:}$ The graphic on the left side shows the delay's power density ${\it \Phi}_{\rm V}(\tau)$ | + | $\text{Example 2:}$ The graphic on the left side shows the delay's power-spectral density ${\it \Phi}_{\rm V}(\tau)$ |
| − | [[File:P ID2177 Mob T 2 3 S8 v3.png|right|frame| | + | [[File:P ID2177 Mob T 2 3 S8 v3.png|right|frame|Multipath spread and coherence bandwidth|class=fit]] |
*with $T_{\rm V} = 1 \ \rm µs$ (red curve), | *with $T_{\rm V} = 1 \ \rm µs$ (red curve), | ||
*with $T_{\rm V} = 2 \ \rm µs$ (blue curve). | *with $T_{\rm V} = 2 \ \rm µs$ (blue curve). | ||
| − | In the right | + | In the right–hand $\varphi_{\rm F}(\Delta f)$ representation, the coherence bandwidths are drawn in: |
*$B_{\rm K} = 276 \ \rm kHz$ (red curve), | *$B_{\rm K} = 276 \ \rm kHz$ (red curve), | ||
*$B_{\rm K} = 138 \ \rm kHz$ (blue curve). | *$B_{\rm K} = 138 \ \rm kHz$ (blue curve). | ||
| + | <br clear=all> | ||
| + | You can see from these numerical values: | ||
| + | *The multipath spread $T_{\rm V}$, obtainable from ${\it \Phi}_{\rm V}(\tau)$ , and the coherence bandwidth $B_{\rm K}$, determined by $\varphi_{\rm F}(\Delta f)$, stand in a fixed relation to each other: | ||
| + | :$$B_{\rm K} \approx 0.276/T_{\rm V}.$$ | ||
| + | *The often [[Mobile_Communications/Multi-Path_Reception_in_Mobile_Communications#Coherence_bandwidth_as_a_function_of_M|$\text{used approximation}$]] $B_{\rm K}\hspace{0.02cm}' \approx 1/T_{\rm V}$ is very inaccurate at exponential ${\it \Phi}_{\rm V}(\tau)$ .}} | ||
| − | + | Let us now consider the time variance characteristics derived from the time correlation function $\varphi_{\rm Z}(\Delta t)$ or from the Doppler's power-spectral density ${\it \Phi}_{\rm D}(f_{\rm D})$ : | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | Let us now consider the time variance characteristics derived from the time correlation function $\varphi_{\rm Z}(\ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ The '''Correlation Time''' $T_{\rm D}$ specifies the average time that must elapse until the channel has completely changed its transmission properties due to the time variance. Its definition is similar to the definition of the coherence bandwidth: | + | $\text{Definition:}$ The »'''Correlation Time'''« $T_{\rm D}$ specifies the average time that must elapse until the channel has completely changed its transmission properties due to the time variance. Its definition is similar to the definition of the coherence bandwidth: |
::<math>\vert \varphi_{\rm Z}(\Delta t = T_{\rm D})\vert \stackrel {!}{=} {1}/{2} \cdot \vert \varphi_{\rm Z}(\Delta t = 0)\vert \hspace{0.05cm}.</math>}} | ::<math>\vert \varphi_{\rm Z}(\Delta t = T_{\rm D})\vert \stackrel {!}{=} {1}/{2} \cdot \vert \varphi_{\rm Z}(\Delta t = 0)\vert \hspace{0.05cm}.</math>}} | ||
| Line 354: | Line 364: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ The '''Doppler Spread''' $B_{\rm D}$ is the average frequency broadening that the individual spectral signal components experience. The calculation is similar to multipath broadening in that the Doppler spread $B_{\rm D}$ is calculated as the standard deviation of the random quantity | + | $\text{Definition:}$ The »'''Doppler Spread'''« $B_{\rm D}$ is the average frequency broadening that the individual spectral signal components experience. The calculation is similar to multipath broadening in that the Doppler spread $B_{\rm D}$ is calculated as the standard deviation of the random quantity $f_{\rm D}$ : |
::<math>B_{\rm D} = \sigma_{\rm D} = \sqrt{ {\rm E} \left [ f_{\rm D}^2 \right ] - m_{\rm D}^2} | ::<math>B_{\rm D} = \sigma_{\rm D} = \sqrt{ {\rm E} \left [ f_{\rm D}^2 \right ] - m_{\rm D}^2} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | *First of all, the Doppler | + | *First of all, the Doppler PDF is to be determined from ${\it \Phi}_{\rm D}(f_{\rm D})$ through area normalization to $1$. |
| + | |||
*This results in the mean Doppler shift $m_{\rm D} = {\rm E}[f_{\rm D}]$ and the standard deviation $\sigma_{\rm D}$.}}<br> | *This results in the mean Doppler shift $m_{\rm D} = {\rm E}[f_{\rm D}]$ and the standard deviation $\sigma_{\rm D}$.}}<br> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
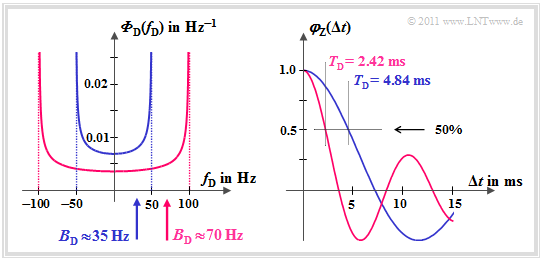
| − | $\text{Example 3:}$ The diagram is valid for a time variant channel without direct component. Shown on the left is the [[Mobile_Communications/ | + | $\text{Example 3:}$ The diagram is valid for a time–variant channel without direct component. Shown on the left is the [[Mobile_Communications/Statistical_Bindings_within_the_Rayleigh_Process#ACF_and_PSD_with_Rayleigh.E2.80.93Fading|$\text{Jakes spectrum}$]] ${\it \Phi}_{\rm D}(f_{\rm D})$. |
[[File:P ID2181 Mob T 2 3 S8b v1.png|right|frame|Doppler spread and correlation time|class=fit]] | [[File:P ID2181 Mob T 2 3 S8b v1.png|right|frame|Doppler spread and correlation time|class=fit]] | ||
The Doppler spread $B_{\rm D}$ can be determined from this: | The Doppler spread $B_{\rm D}$ can be determined from this: | ||
| Line 372: | Line 383: | ||
The time correlation function $\varphi_{\rm Z}(\Delta t)$ is sketched on the right, as the Fourier transform of ${\it \Phi}_{\rm D}(f_{\rm D})$ . | The time correlation function $\varphi_{\rm Z}(\Delta t)$ is sketched on the right, as the Fourier transform of ${\it \Phi}_{\rm D}(f_{\rm D})$ . | ||
| − | This can be expressed given boundary conditions | + | This can be expressed for given boundary conditions with the Bessel function ${\rm J}_0()$ as: |
| − | ::<math>\varphi_{\rm Z}(\Delta t \hspace{-0.05cm} = \hspace{-0.05cm}T_{\rm D}) \hspace{-0.05cm}= \hspace{-0.05cm} {\rm J}_0(2 \pi \hspace{-0.05cm} \cdot \hspace{-0.05cm} f_{\rm D,\hspace{0. | + | ::<math>\varphi_{\rm Z}(\Delta t \hspace{-0.05cm} = \hspace{-0.05cm}T_{\rm D}) \hspace{-0.05cm}= \hspace{-0.05cm} {\rm J}_0(2 \pi \hspace{-0.05cm} \cdot \hspace{-0.05cm} f_{\rm D,\hspace{0.1cm}max} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\Delta t ).</math> |
| − | *The correlation duration of the blue curve is $T_{\rm D} = 4.84 \ \rm ms$. | + | *The correlation duration of the blue curve is $T_{\rm D} = 4.84 \ \rm ms$. |
| − | *For $f_{\rm D,\hspace{0. | + | |
| − | *In this case, it | + | *For $f_{\rm D,\hspace{0.1cm}max} = 100\,{\rm Hz}$ the correlation duration is only half. |
| + | |||
| + | *In this case, it generally applies: $B_{\rm D} \cdot T_{\rm D}\approx 0.17$.}} | ||
<br clear=all> | <br clear=all> | ||
== Simulation according to the GWSSUS model == | == Simulation according to the GWSSUS model == | ||
<br> | <br> | ||
| − | The | + | The »'''Monte–Carlo method'''«, here described for the simulation of a GWSSUS mobile communication channel, is based on work by Rice [Ric44]<ref name='Ric44'>Rice, S.O.: Mathematical Analysis of Random Noise. BSTJ–23, pp. 282–332 und BSTJ–24, pp. 45–156, 1945.</ref> and Höher [Höh90]<ref name='Höh90'>Höher, P.: Empfang trelliscodierter PSK–Signale auf frequenzselektiven Mobilfunkkanälen – Entzerrung, Decodierung und Kanalschätzung. Düsseldorf: VDI–Verlag, Fortschrittsberichte, Reihe 10, Nr. 147, 1990.</ref>. |
| − | *The | + | *The two–dimensional impulse response is represented by a sum of $M$ complex exponential functions. $M$ can be interpreted as the number of different paths: |
::<math>h(\tau,\ t)= \frac{1}{\sqrt {M}} \cdot \sum_{m=1}^{M} \alpha_m \cdot \delta (t - \tau_m) \cdot {\rm e}^{{\rm j} \hspace{0.05cm} \phi_{m} }\cdot {\rm e}^{ {\rm j} \hspace{0.05cm}2 \pi f_{{\rm D},\hspace{0.05cm} m} t} | ::<math>h(\tau,\ t)= \frac{1}{\sqrt {M}} \cdot \sum_{m=1}^{M} \alpha_m \cdot \delta (t - \tau_m) \cdot {\rm e}^{{\rm j} \hspace{0.05cm} \phi_{m} }\cdot {\rm e}^{ {\rm j} \hspace{0.05cm}2 \pi f_{{\rm D},\hspace{0.05cm} m} t} | ||
\hspace{0.05cm}. </math> | \hspace{0.05cm}. </math> | ||
| − | *First, the delays $\tau_m$, the attenuation factors $\alpha_m$, the equally distributed phases $\phi_m$ and the Doppler frequencies $f_{{\rm D},\hspace{0. | + | *First, the delays $\tau_m$, the attenuation factors $\alpha_m$, the equally distributed phases $\phi_m$ and the Doppler frequencies $f_{{\rm D},\hspace{0.1cm} m}$ will be randomly generated according to the GWSSUS specifications. The base for the random generation of the Doppler frequencies $f_{{\rm D},\hspace{0.1cm} m}$ is the [[Mobile_Communications/Statistical_Bindings_within_the_Rayleigh_Process#Doppler_frequency_and_its_distribution| $\text{Jakes spectrum}$]] ${\it \Phi}_{\rm D}(f_{\rm D})$, which, appropiately normalized, simultaneously indicates the probability density function $\rm (PDF)$ of the Doppler frequencies.<br> |
| − | *Because of ${\it \Phi}_{\rm VD}(\tau, f_{\rm D}) = {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})$  the delay time $\tau_m$ is independent of the Doppler frequency $f_{{\rm D},\hspace{0. | + | *Because of ${\it \Phi}_{\rm VD}(\tau, f_{\rm D}) = {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})$ the delay time $\tau_m$ is independent of the Doppler frequency $f_{{\rm D},\hspace{0.1cm} m}$ for all $m$. This is valid with good approximation for terrestrial land mobile communication. For the random generation of the parameters $\alpha_m$ and $\tau_m$, which determine the delay–power-spectral density $ {\it \Phi}_{\rm V}(\tau)$ the following [[Mobile_Communications/The_GWSSUS_Channel_Model#Power_density_spectrum_of_the_time-variant_impulse_response|$\text{COST profiles}$]] are available: $\rm RA$ ("Rural Area"), $\rm TU$ ("Typical Urban"), $\rm BU$ ("Bad Urban") and $\rm HT$ ("Hilly Terrain"). <br> |
| − | *The greater the number of different paths $M$ is chosen for the simulation, the better a real impulse response is approximated by the above equation. However, the higher accuracy of the | + | *The greater the number of different paths $M$ is chosen for the simulation, the better a real impulse response is approximated by the above equation. However, the higher accuracy of the simulation is at the expense of its duration. In the literature, favorable values are given for $M$ between $100$ and $600$ . <br> |
| − | [[File:P ID2183 Mob T 2 3 S9a.png|right|frame|Time variant transfer function | + | [[File:P ID2183 Mob T 2 3 S9a.png|right|frame|Time-variant transfer function $($the absolute value squared is simulated$)$]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
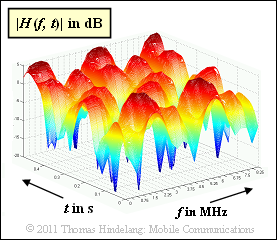
| − | $\text{Example 4:}$ The graphic from [Hin08]<ref name='Hin08'>Hindelang, T.: | + | $\text{Example 4:}$ The graphic from [Hin08]<ref name='Hin08'>Hindelang, T.: Mobile Communications. |
| − | + | Lecture notes. Institute for Communications Engineering. Munich: Technical University of Munich, 2008.</ref> shows a simulation result: $20 \cdot \lg \vert H(f, \hspace{0.1cm}t)\vert$ is shown as a 2D plot, where the time-variant transfer function $H(f, \hspace{0.1cm}t)$ is also referred to as $\eta_{\rm FZ}(f, \hspace{0.1cm}t)$ in this tutorial.<br> | |
The simulation is based on the following parameters: | The simulation is based on the following parameters: | ||
| − | *The time variance results from a movement with $v = 3 \ \rm km/h$. | + | *The time variance results from a movement with $v = 3 \ \rm km/h$. |
| + | |||
*The carrier frequency is $f_{\rm T} = 2 \ \rm GHz$.<br> | *The carrier frequency is $f_{\rm T} = 2 \ \rm GHz$.<br> | ||
*The maximum delay time is $\tau_{\rm max} \approx 0.4 \ \rm µ s$. | *The maximum delay time is $\tau_{\rm max} \approx 0.4 \ \rm µ s$. | ||
| + | |||
* According to the approximation we obtain the coherence bandwidth $B_{\rm K}\hspace{0.02cm}' \approx 2.5 \ \rm MHz$.<br> | * According to the approximation we obtain the coherence bandwidth $B_{\rm K}\hspace{0.02cm}' \approx 2.5 \ \rm MHz$.<br> | ||
*The maximum Doppler frequency is $f_\text{D, max} \approx 5.5 \ \rm Hz$. | *The maximum Doppler frequency is $f_\text{D, max} \approx 5.5 \ \rm Hz$. | ||
| + | |||
* The Doppler spread results in $B_{\rm D} \approx 4 \ \rm Hz$.}} | * The Doppler spread results in $B_{\rm D} \approx 4 \ \rm Hz$.}} | ||
<br clear=all> | <br clear=all> | ||
| − | ==Exercises | + | ==Exercises for the chapter== |
<br> | <br> | ||
[[Aufgaben:Exercise 2.5: Scatter Function]] | [[Aufgaben:Exercise 2.5: Scatter Function]] | ||
| Line 427: | Line 443: | ||
[[Aufgaben:Exercise 2.9: Coherence Time]] | [[Aufgaben:Exercise 2.9: Coherence Time]] | ||
| − | == | + | ==References== |
<references/> | <references/> | ||
Latest revision as of 17:38, 30 January 2023
Contents
- 1 Generalized system functions of time variant-systems
- 2 Simplifications due to the GWSSUS requirements
- 3 Auto-correlation function of the time-variant impulse response
- 4 Power-spectral density of the time-variant impulse response
- 5 ACF and PSD of the frequency-variant transfer function
- 6 ACF and PSD of the delay-Doppler function
- 7 ACF and PSD of the time-variant transfer function
- 8 Parameters of the GWSSUS model
- 9 Simulation according to the GWSSUS model
- 10 Exercises for the chapter
- 11 References
Generalized system functions of time variant-systems
Linear time-invariant systems $\rm (LTI)$ can be completely described with only two system functions,
- the transfer function $H(f)$ and
- the impulse response $h(t)$ ⇒ after renaming $h(\tau)$.
In contrast, four different functions are possible with time-variant systems $\rm (LTV)$ . A formal distinction of these functions with regard to time and frequency domain representation by lowercase and uppercase letters is thus excluded.
Therefore a nomenclature change will be made, which can be formalized as follows:
- The four possible system functions are uniformly denoted by $\boldsymbol{\eta}_{12}$ .
- The first subindex is either a $\boldsymbol{\rm V}$ $($because of German $\rm V\hspace{-0.05cm}$erzögerung ⇒ delay time $\tau)$ or a $\boldsymbol{\rm F}$ $($frequency $f)$.
- Either a $\boldsymbol{\rm Z}$ $($because of German $\rm Z\hspace{-0.05cm}$eit ⇒ time $t)$ or a $\boldsymbol{\rm D}$ $($Doppler frequency $f_{\rm D})$ is possible as the second subindex.
Since, in contrast to line-based transmission, the system functions of mobile communications cannot be described deterministically, but are statistical variables, the corresponding correlation functions must be considered later on.
In the following, we will refer to these as $\boldsymbol{\varphi}_{12}$, and use the same indices as for the system functions $\boldsymbol{\eta}_{12}$.
- These formalized designations are inscribed in the graphic in blue letters.
- Additionally, the designations used in other chapters or literature are given (gray letters). In the other chapters these are also partly used.
${\rm (1)}$ At the top you can see the »time-variant impulse response« ${\eta}_{\rm VZ}(\tau,\hspace{0.05cm} t) \equiv h(\tau,\hspace{0.05cm} t)$ in the "delay–time range". The associated auto-correlation function $\rm (ACF)$ is
- \[\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = {\rm E} \big[ \eta_{\rm VZ}(\tau_1,\hspace{0.05cm} t_1) \cdot \eta_{\rm VZ}^{\star}(\tau_2, t_2) \big]\hspace{0.05cm}. \]
${\rm (2)}$ For the "frequency–time representation" you get the »time-variant transfer function« ${\eta}_{\rm FZ}(f,\hspace{0.05cm} t) \equiv H(f,\hspace{0.05cm} t)$.
The Fourier transform with respect to $\tau$ is represented in the graph by ${\rm F}_\tau\hspace{0.05cm}[ \cdot ]$ . The Fourier integral is written out in full:
- \[\eta_{\rm FZ}(f, \hspace{0.05cm} t) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau,\hspace{0.05cm} t) \cdot {\rm e}^{- {\rm j}\cdot 2 \pi f \tau}\hspace{0.15cm}{\rm d}\tau \hspace{0.05cm}, \hspace{0.3cm} \text{kurz:} \hspace{0.2cm} \eta_{\rm FZ}(f, t) \hspace{0.2cm} \stackrel{f, \hspace{0.05cm} \tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t) \hspace{0.05cm}.\]
- The ACF of this time-variant transfer function is generally:
- \[\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) = {\rm E} \big [ \eta_{\rm FZ}(f_1, t_1) \cdot \eta_{\rm FZ}^{\star}(f_2, t_2) \big ]\hspace{0.05cm}.\]
${\rm (3)}$ The »Scatter–Function« ${\eta}_{\rm VD}(\tau,\hspace{0.05cm} f_{\rm D}) \equiv s(\tau,\hspace{0.05cm} f_{\rm D})$ corresponding to the left block describes the mobile communications channel in the "delay–Doppler area".
$f_{\rm D}$ describes the $\text{Doppler frequency}$. The scatter function results from ${\eta}_{\rm VZ}(\tau,\hspace{0.05cm} t)$ through Fourier transformation with respect to the second parameter $t$:
- \[ \eta_{\rm VD}(\tau, f_{\rm D}) \hspace{0.2cm} \stackrel{f_{\rm D}, \hspace{0.05cm}t}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau, t)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \varphi_{\rm VD}(\tau_1, f_{\rm D_1}, \tau_2, f_{\rm D_2}) = {\rm E} \left [ \eta_{\rm VD}(\tau_1, f_{\rm D_1}) \cdot \eta_{\rm VD}^{\star}(\tau_2, f_{\rm D_2}) \right ] \hspace{0.05cm}.\]
${\rm (4)}$ Finally, we consider the so-called »frequency-variant transfer function« $\eta_{\rm FD}(f, f_{\rm D})$, i.e. the "frequency–Doppler representation".
According to the graph, this can be reached in two ways:
- $$\eta_{\rm FD}(f, f_{\rm D}) \hspace{0.2cm} \stackrel{f_{\rm D}, \hspace{0.05cm}t}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm FZ}(f, t)\hspace{0.05cm},\hspace{0.5cm}\eta_{\rm FD}(f, f_{\rm D}) \hspace{0.2cm} \stackrel{f, \hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VD}(\tau, f_{\rm D})\hspace{0.05cm}.$$
$\text{Notes:}$
- The specified Fourier correlations between the system functions in the graph are illustrated by the outer, dark green arrows and are marked with ${\rm F}_p\hspace{0.05cm}[\hspace{0.05cm} \cdot \hspace{0.05cm}]$ ,
the index $p$ indicates to which parameter $\tau$, $f$, $t$ or $f_{\rm D}$ does the Fourier transformation refer.
- The inner (lighter) arrows indicate the links via the $\text{inverse Fourier transform}$. For this we use the notation ${ {\rm F}_p}^{-1}\hspace{0.05cm}[ \hspace{0.05cm} \cdot \hspace{0.05cm} ]$.
- The applet "Impulses and Spectra" illustrates the connection between the time and frequency domain, which can be described by formulas using Fourier transformation and Fourier inverse transformation.
Simplifications due to the GWSSUS requirements
The general relationship between the four system functions is very complicated due to non-stationary effects.
Compared to the general model, some limitations have to be made in order to arrive at a suitable model for the mobile communications channel from which relevant statements for practical applications can be derived.
The following definitions lead to the $\rm GWSSUS$ model
$( \rm G$aussian $\rm W$ide $\rm S$ense $\rm S$tationary $\rm U$ncorrelated $\rm S$cattering$)$:
- The random process of the channel impulse response $h(\tau,\hspace{0.1cm} t) = {\eta}_{\rm VZ}(\tau,\hspace{0.1cm} t)$ is generally assumed to be complex (i.e., description in the equivalent low-pass range), Gaussian $($identifier $\rm G)$ and zero-mean (Rayleigh, not Rice, that means, no line of sight) .
- The random process is weakly stationary ⇒ its characteristics change only slightly with time, and the ACF $ {\varphi}_{\rm VZ}(\tau_1,\hspace{0.05cm} t_1,\hspace{0.05cm}\tau_2,\hspace{0.05cm} t_2)$ of the time-variant impulse response does not depend on the absolute times $t_1$ and $t_2$ but only on the time difference $\Delta t = t_2 - t_1$. This is indicated by the identifier $\rm WSS$ ⇒ $\rm W$ide $\rm S$ense $\rm S$tationary.
- The individual echoes due to multipath propagation are uncorrelated, which is expressed by the identifier $\rm US$ ⇒ $\rm U$ncorrelated $\rm S$cattering.
The mobile communications channel can be described in full according to this graph. The individual power-spectral densities (labeled blue) and the correlation function (labeled red) is explained in detail in the following sections.
Auto-correlation function of the time-variant impulse response
We now consider the $\text{auto-correlation function}$ $\rm (ACF)$ of the time-variant impulse response ⇒ $h(\tau,\hspace{0.1cm} t) = {\eta}_{\rm VZ}(\tau,\hspace{0.1cm} t)$ more closely. It shows:
- Based on the $\rm WSS$ property, the auto-correlation function can be written with $\Delta t = t_2 - t_1$ :
- \[\varphi_{\rm VZ}(\tau_1, t_1, \tau_2, t_2) = \varphi_{\rm VZ}(\tau_1, \tau_2, \Delta t)\hspace{0.05cm}.\]
- Since the echoes were assumed to be independent of each other $\rm (US$ property$)$, the impulse response can be assumed to be uncorrelated with respect to the delays $\tau_1$ and $\tau_2$. Then:
- \[\varphi_{\rm VZ}(\tau_1, \tau_2, \Delta t) = 0 \hspace{0.35cm}{\rm f\ddot{u}r}\hspace{0.35cm} \tau_1 \ne \tau_2\hspace{0.05cm}. \]
- If one now replaces $\tau_1$ with $\tau$ and $\tau_2$ with $\tau + \Delta \tau$, this auto-correlation function can be represented in the following way:
- \[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}. \]
- Because of the convolution property of the Dirac delta function, the ACF for $\tau_1 \ne \tau_2$ ⇒ $\Delta \tau \ne 0$ disappears.
- $ {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.1cm}$ is the »delay–time's cross power-spectral density«, which depends on the delay $\tau \ (= \tau_1 =\tau_2)$ and on the time difference $\Delta t = t_2 - t_1$ .
$\text{Please note:}$
- With this approach, the auto-correlation function $\varphi_{\rm VZ}(\Delta \tau, \Delta t)$ and the power-spectral density ${\it \Phi}_{\rm VZ}(\tau, \Delta t) $ are not connected via the Fourier transform as usual, but are linked via a Dirac delta function:
- \[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}. \]
- Not all symmetry properties that follow from the $\text{Wiener–Khintchine theorem}$ are thus given here. In particular it is quite possible and even very likely that such a power-spectral density is an odd function.
In the overview in the last section, the »delay–time's cross power-spectral density« ${\it \Phi}_{\rm VZ}(\tau, \Delta t) $ can be seen in the top middle.
- Since $\eta_{\rm VZ}(\tau, t) $, like any $\text{impulse response}$, has the unit $\rm [1/s]$ , the auto-correlation function has the unit $\rm [1/s^2]$:
- \[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = {\rm E} \left [ \eta_{\rm VZ}(\tau, t) \cdot \eta_{\rm VZ}^{\star}(\tau + \Delta \tau, t + \Delta t) \right ].\]
- But since the Dirac delta function with the time argument $\delta(\Delta \tau)$ also has the unit $\rm [1/s]$ the delay–time's cross power-spectral density ${\it \Phi}_{\rm VZ}(\tau, \Delta t) $ also has the unit $\rm [1/s]$:
- \[\varphi_{\rm VZ}(\Delta \tau, \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.05cm}.\]
Power-spectral density of the time-variant impulse response
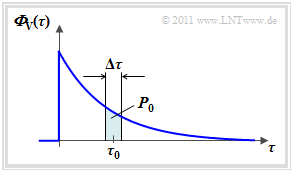
One obtains the »delay's power-spectral density« ${\it \Phi}_{\rm V}(\Delta \tau)$ by setting the second parameter of ${\it \Phi}_{\rm VZ}(\Delta \tau, \Delta t)$ to $\Delta t = 0$ . The graphic on the right shows an exemplary curve.
The delay's power-spectral density is a central quantity for the description of the mobile communications channel. This has the following characteristics:
- ${\it \Phi}_{\rm V}(\Delta \tau_0)$ is a measure for the "power" of those signal components which are delayed by $\tau_0$ . For this purpose, an implicit averaging over all Doppler frequencies $(f_{\rm D})$ is carried out.
- The delay's power-spectral density ${\it \Phi}_{\rm V}(\Delta \tau)$ has, like ${\it \Phi}_{\rm VZ}(\Delta \tau, \Delta t)$ , the unit $\rm [1/s]$. It characterizes the power distribution over all possible delays $\tau$.
- In the graphic, the power $ P_0 \approx {\it \Phi}_{\rm V}(\Delta \tau_0)\cdot \Delta \tau$ of those signal components that arrive at the receiver via any path with a delay between $\tau_0 \pm \Delta \tau/2$.
- Normalizing the power-spectral density ${\it \Phi}_{\rm V}(\Delta \tau)$ in such a way that the area is $1$ results in the probability density function $\rm (PDF)$ of the delay time:
- \[{\rm PDF}_{\rm V}(\tau) = \frac{{\it \Phi}_{\rm V}(\tau)}{\int_{0 }^{\infty}{\it \Phi}_{\rm V}(\tau)\hspace{0.15cm}{\rm d}\tau} \hspace{0.05cm}.\]
Note on nomenclature:
- In the book "Stochastic Signal Theory" we would have denoted this $\text{probability density function}$ with $f_\tau(\tau)$.
- To make the relation between ${\it \Phi}_{\rm V}(\Delta \tau)$ and the PDF clear and to avoid confusion with the frequency $f$ we use the nomenclature given here.
$\text{Example 1: Delay models according to COST 207}$
In the 1990s, the European Union founded the working group COST 207 with the aim to provide standardized channel models for cellular mobile communications. where "COST" stands for "European Cooperation in Science and Technology".
In this international committee profiles for the delay time $\tau$ have been developed, based on measurements and valid for different application scenarios. In the following, four different delay's power-spectral densities are given, where the normalization factor ${\it \Phi}_0 = {\it \Phi}_{\rm V}(\tau = 0)$ is always used. The graph shows the PSDs of these profiles in logarithmic representation:
(1) profile $\rm RA$ ("Rural Area"):
- \[{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} \hspace{0.3cm}\text{for}\hspace{0.2cm} 0 < \tau < 0.7\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 0.109\,{\rm µ s}\hspace{0.05cm}.\]
(2) profile $\rm TU$ ("Typical Urban") ⇒ cities and suburbs:
- \[{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = {\rm e}^{ -\tau / \tau_0} \hspace{0.3cm}\text{for}\hspace{0.2cm} 0 < \tau < 7\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s}\hspace{0.05cm}.\]
(3) profile $\rm BU$ ("Bad Urban") ⇒ unfavourable conditions in cities:
- \[{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0}\\ 0.5 \cdot {\rm e}^{ (5\,{\rm µ s}-\tau) / \tau_0} \end{array} \right.\quad \begin{array}{*{1}l} \hspace{0.1cm} {\rm for}\hspace{0.3cm} 0 < \tau < 5\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s}\hspace{0.05cm}, \\ \hspace{0.1cm} {\rm for}\hspace{0.3cm} 5\,{\rm µ s} < \tau < 10\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}. \\ \end{array}\]
(4) profile $\rm HT$ ("Hilly Terrain") ⇒ hilly and mountainous regions:
- \[{\it \Phi}_{\rm V}(\tau)/{\it \Phi}_{\rm 0} = \left\{ \begin{array}{c} {\rm e}^{ -\tau / \tau_0}\\ 0.04 \cdot {\rm e}^{ (15\,{\rm µ s}-\tau) / \tau_0} \end{array} \right.\quad \begin{array}{*{1}l} \hspace{-0.25cm} {\rm for}\hspace{0.3cm} 0 < \tau < 2\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 0.286\,{\rm µ s}\hspace{0.05cm}, \\ \hspace{-0.25cm} {\rm for}\hspace{0.3cm} 15\,{\rm µ s} < \tau < 20\,{\rm µ s}\hspace{0.05cm},\hspace{0.15cm}\tau_0 = 1\,{\rm µ s} \hspace{0.05cm}. \\ \end{array}\]
One can see from the graphics:
- The exponential functions in linear representation now become straight lines.
- For logarithmic display, you can read the PSD parameter $\tau_0$ for $\rm 10 \cdot lg \ (1/e) = -4.34 \ dB$ as shown in the graph for the $\rm TU$ profile.
- These four COST profiles are described in the "Exercise 2.8" in more detail.
ACF and PSD of the frequency-variant transfer function
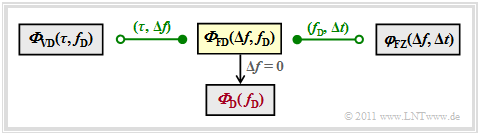
The system function $\eta_{\rm FD}(f, f_{\rm D})$ described in the "overview in the first section of this chapter" is also known as the "Frequency-variant Transfer Function" where the adjective "frequency-variant" refers to the Doppler frequency $f_{\rm D}$.
The associated auto-correlation function $\rm (ACF)$ is defined as follows:
- \[\varphi_{\rm FD}(f_1, f_{\rm D_1}, f_2, f_{\rm D_2}) = {\rm E} \left [ \eta_{\rm FD}(f_1, f_{\rm D_1}) \cdot \eta_{\rm FZ}^{\star}(f_2, f_{\rm D_2}) \right ]\hspace{0.05cm}. \]
By similar considerations as in the "previous section" this auto-correlation function can be represented under GWSSUS conditions as follows
- \[\varphi_{\rm FD}(\Delta f, \Delta f_{\rm D}) = \delta(\Delta f_{\rm D}) \cdot {\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) \hspace{0.05cm}.\]
The following applies:
- ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ is the so-called »frequency–Doppler's cross power-spectral density«, which is highlighted in the graphic by a yellow background.
- The first argument $\Delta f = f_2 - f_1$ takes into account that ACF and PSD depend only on the frequency difference due to the "stationarity" .
- The factor $\delta (\Delta f_{\rm D})$ with $\Delta f_{\rm D} = f_{\rm D_2} - f_{\rm D_1}$ expresses the "uncorrelation of the PSD" with respect to the Doppler shift.
- You get from ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ to »Doppler's power-spectral density« ${\it \Phi}_{\rm D}(f_{\rm D})$ if you set $\Delta f= 0$.
- The Doppler's power-spectral density ${\it \Phi}_{\rm D}(f_{\rm D})$ indicates the power with which individual Doppler frequencies occur.
- The probability density function $\rm (PDF)$ of the Doppler frequency is obtained from ${\it \Phi}_{\rm D}(f_{\rm D})$ by suitable normalization. The PDF has like ${\it \Phi}_{\rm D}(f_{\rm D})$ the unit $\rm [1/Hz]$.
- \[{\rm PDF}_{\rm D}(f_{\rm D}) = \frac{{\it \Phi}_{\rm D}(f_{\rm D})}{\int_{-\infty }^{+\infty}{\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.15cm}{\rm d}f_{\rm D}} \hspace{0.05cm}.\]
- Often, for example for a vertical monopulse antenna in an isotropically scattered field, the ${\it \Phi}_{\rm D}(f_{\rm D})$ is given by the $\text{Jakes spectrum}$ .
The frequency–Doppler's cross power-spectral density ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ is highlighted in yellow. The Fourier connections to the neighboring GWSSUS system description functions ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$ and ${\it \varphi}_{\rm FZ}(\Delta f, \Delta t)$ are also marked.
We refer here to the interactive applet "The Doppler Effect".
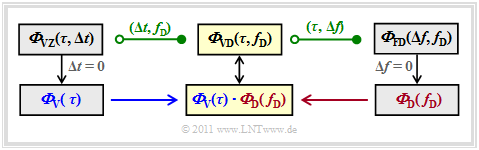
ACF and PSD of the delay-Doppler function
The system function shown in the "overview in the first section of this chapter" on the left hand side was named $\eta_{\rm VD}(\tau, f_{\rm D})$ .
The auto-correlation function $\rm (ACF)$ of this delay–Doppler function can be written with $\Delta \tau = \tau_2 - \tau_1$ and $\Delta f_{\rm D} = f_{\rm D2} - f_{\rm D1}$ taking into account the GWSSUS properties with $\Delta \tau = \tau_2 - \tau_1$ and $\Delta f_{\rm D} = f_{\rm D2} - f_{\rm D1}$ as follows
- \[\varphi_{\rm VD}(\tau_1, f_{\rm D_1}, \tau_2, f_{\rm D_2}) = \varphi_{\rm VD}(\Delta \tau, \Delta f_{\rm D}) = \delta(\Delta \tau) \cdot {\rm \delta}(\Delta f_{\rm D}) \cdot {\it \Phi}_{\rm VD}(\tau, f_{\rm D}) \hspace{0.05cm}.\]
It should be noted about this equation:
- The first Dirac delta function $\delta (\Delta \tau)$ takes into account that the delays are uncorrelated ("Uncorrelated Scattering").
- The second Dirac delta function $\delta (\Delta f_{\rm D})$ follows from the stationarity ("Wide Sense Stationary").
- The delay–Doppler's power-spectral density ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$ , also called »Scatter Function« can be calculated from ${\it \Phi}_{\rm VZ}(\tau, \Delta t)$ or ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ as follows:
- \[{\it \Phi}_{\rm VD}(\tau, f_{\rm D}) ={\rm F}_{\Delta t} \big [ {\it \Phi}_{\rm VZ}(\tau, \Delta t) \big ] = \int_{-\infty}^{+\infty} {\it \Phi}_{\rm VZ}(\tau, \Delta t) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm D} \hspace{0.05cm}\cdot \hspace{0.05cm}\Delta t}\hspace{0.15cm}{\rm d}\Delta t \hspace{0.05cm},\]
- \[{\it \Phi}_{\rm VD}(\tau, f_{\rm D}) = {\rm F}_{f_{\rm D}}^{-1} \big [ {\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) \big ] = \int_{-\infty}^{+\infty} {\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) \cdot {\rm e}^{+{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \tau \hspace{0.05cm}\cdot \hspace{0.05cm} \Delta f}\hspace{0.15cm}{\rm d}\Delta f \hspace{0.05cm}. \]
- Both, the system function $\eta_{\rm VD}(\tau, f_{\rm D})$ and the derived functions $\varphi _{\rm VD}(\Delta \tau, \Delta f_{\rm D})$ and ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$, are dimensionless. For more information on this, see the specification for "Exercise 2.6".
- Furthermore, if the GWSSUS requirements are met, the scatter function is equal to the product of the delay's and Doppler's PSDs:
- \[{\it \Phi}_{\rm VD}(\tau, f_{\rm D}) = {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.05cm}.\]
$\text{Conclusion:}$
The figure summarizes the results of this chapter so far. It should be noted:
(1) The influence of the delay time $\tau$ and the Doppler frequency $f_{\rm D}$ can be separated
- into the blue power-spectral density ${\it \Phi}_{\rm V}(\tau)$
- and the red power-spectral density ${\it \Phi}_{\rm D}(f_{\rm D})$.
(2) The two–dimensional delay–Doppler's power-spectral density ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$ is equal to the product of these two functions.
ACF and PSD of the time-variant transfer function
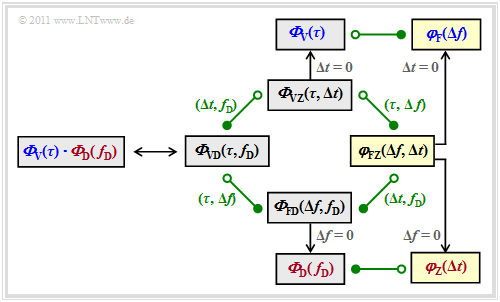
The following diagram shows all the relationships between the individual power-spectral densities once again in compact form.
This has already been discussed in the last sections:
- $${\it \Phi}_{\rm VZ}(\tau, \Delta t)\hspace{0.55cm}\Rightarrow \hspace{0.3cm}\text{with} \hspace{0.2cm}\Delta t = 0\text{:} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau),$$
- $${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{with} \hspace{0.2cm}\Delta f = 0\text{:} \hspace{0.2cm} {\it \Phi}_{\rm D}( f_{\rm D}),$$
- $${\it \Phi}_{\rm VD}(\tau, f_{\rm D})= {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.05cm}.$$
The »frequency–time's correlation function« (marked yellow in the adjacent graph) has not yet been considered:
- \[\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) = {\rm E} \left [ \eta_{\rm FZ}(f_1, t_1) \cdot \eta_{\rm FZ}^{\star}(f_2, t_2) \right ]\hspace{0.05cm}.\]
Considering again the GWSSUS simplifications and the identity $\eta_{\rm FZ}(f, \hspace{0.05cm}t) \equiv H(f, \hspace{0.05cm}t)$, the ACF can be also written with $\Delta f = f_2 - f_1$ and $\Delta t = t_2 - t_1$ as follows:
- \[\varphi_{\rm FZ}(f_1, t_1, f_2, t_2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\varphi_{\rm FZ}(\Delta f, \Delta t) = {\rm E} \big [ H(f, t) \cdot H^{\star}(f + \Delta f, t + \Delta t) \big ]\hspace{0.05cm}.\]
It should be noted in this respect:
- You already can see from the name that $\varphi_{\rm FZ}(\Delta f, \Delta t)$ is a correlation function and not a PSD like the functions ${\it \Phi}_{\rm VZ}(\tau, \Delta t)$, ${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D})$ and ${\it \Phi}_{\rm VD}(\tau, f_{\rm D})$.
- The Fourier relationships with the neighboring functions are:
- \[{\it \Phi}_{\rm VZ}(\tau, \Delta t) \hspace{0.2cm} \stackrel{\tau, \hspace{0.05cm}\Delta f}{\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} \varphi_{\rm FZ}(\Delta f, \hspace{0.05cm}\Delta t) \hspace{0.2cm} \stackrel{\Delta t,\hspace{0.05cm} f_{\rm D}}{\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} {\it \Phi}_{\rm FD}(\Delta f,\hspace{0.05cm} f_{\rm D}) \hspace{0.05cm}.\]
- If you set the parameters $\Delta t = 0$ or $\Delta f = 0$ in this two–dimensional function, the separate correlation functions for the frequency domain or the time domain result:
- $$\varphi_{\rm F}(\Delta f) = \varphi_{\rm FZ}(\Delta f, \Delta t = 0) \hspace{0.05cm},\hspace{0.5cm} \varphi_{\rm Z}(\Delta t) = \varphi_{\rm FZ}(\Delta f = 0, \Delta t ) \hspace{0.05cm}.$$
- From the graph it is also clear that these correlation functions correspond to the derived power-spectral densities via the Fourier transform:
- \[\varphi_{\rm F}(\Delta f) \hspace{0.2cm} {\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau)\hspace{0.05cm},
\hspace{0.4cm}\varphi_{\rm Z}(\Delta t) \hspace{0.2cm} {\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} {\it \Phi}_{\rm D}(f_{\rm D})\hspace{0.05cm}.\]
Parameters of the GWSSUS model
According to the results in the last section, the mobile channel is replaced by
- the delay's power-spectral density ${\it \Phi}_{\rm V}(\tau)$ and
- the Doppler's power-spectral density ${\it \Phi}_{\rm D}(f_{\rm D})$.
By suitable normalization to the respective area $1$ the density functions result with respect to the delay time $\tau$ or the Doppler frequency $f_{\rm D}$.
Characteristic values can be derived from the power-spectral densities or the corresponding correlation functions. The most important ones are listed here:
$\text{Definition:}$ The »Multipath Spread« or »Time Delay Spread« $T_{\rm V}$ specifies the spread that a Dirac delta experiences through the channel on statistical average.
$T_{\rm V}$ is defined as the standard deviation $(\sigma_{\rm V})$ the random variable $\tau$:
- \[T_{\rm V} = \sigma_{\rm V} = \sqrt{ {\rm E} \big [ \tau^2 \big ] - m_{\rm V}^2} \hspace{0.05cm}.\]
- The mean value $m_{\rm V} = {\rm E}\big[\tau \big]$ is an "Average Excess Delay" for all signal components.
- ${\rm E} \big [ \tau^2 \big ] $ is to be calculated as the root mean square value.
$\text{Definition:}$ The »Coherence Bandwidth« $B_{\rm K}$ is the $\Delta f$ value at which the frequency's correlation function has dropped to half of its value for the first time.
- \[\vert \varphi_{\rm F}(\Delta f = B_{\rm K})\vert \stackrel {!}{=} {1}/{2} \cdot \vert \varphi_{\rm F}(\Delta f = 0)\vert \hspace{0.05cm}.\]
- $B_{\rm K}$ is a measure of the minimum frequency difference by which two harmonic oscillations must differ in order to have completely different channel transmission characteristics.
- If the signal bandwidth is $B_{\rm S} <B_{\rm K}$, then all spectral components are changed in approximately the same way by the channel.
This means: Precisely then there is a non-frequency selective fading.
$\text{Example 2:}$ The graphic on the left side shows the delay's power-spectral density ${\it \Phi}_{\rm V}(\tau)$
- with $T_{\rm V} = 1 \ \rm µs$ (red curve),
- with $T_{\rm V} = 2 \ \rm µs$ (blue curve).
In the right–hand $\varphi_{\rm F}(\Delta f)$ representation, the coherence bandwidths are drawn in:
- $B_{\rm K} = 276 \ \rm kHz$ (red curve),
- $B_{\rm K} = 138 \ \rm kHz$ (blue curve).
You can see from these numerical values:
- The multipath spread $T_{\rm V}$, obtainable from ${\it \Phi}_{\rm V}(\tau)$ , and the coherence bandwidth $B_{\rm K}$, determined by $\varphi_{\rm F}(\Delta f)$, stand in a fixed relation to each other:
- $$B_{\rm K} \approx 0.276/T_{\rm V}.$$
- The often $\text{used approximation}$ $B_{\rm K}\hspace{0.02cm}' \approx 1/T_{\rm V}$ is very inaccurate at exponential ${\it \Phi}_{\rm V}(\tau)$ .
Let us now consider the time variance characteristics derived from the time correlation function $\varphi_{\rm Z}(\Delta t)$ or from the Doppler's power-spectral density ${\it \Phi}_{\rm D}(f_{\rm D})$ :
$\text{Definition:}$ The »Correlation Time« $T_{\rm D}$ specifies the average time that must elapse until the channel has completely changed its transmission properties due to the time variance. Its definition is similar to the definition of the coherence bandwidth:
- \[\vert \varphi_{\rm Z}(\Delta t = T_{\rm D})\vert \stackrel {!}{=} {1}/{2} \cdot \vert \varphi_{\rm Z}(\Delta t = 0)\vert \hspace{0.05cm}.\]
$\text{Definition:}$ The »Doppler Spread« $B_{\rm D}$ is the average frequency broadening that the individual spectral signal components experience. The calculation is similar to multipath broadening in that the Doppler spread $B_{\rm D}$ is calculated as the standard deviation of the random quantity $f_{\rm D}$ :
- \[B_{\rm D} = \sigma_{\rm D} = \sqrt{ {\rm E} \left [ f_{\rm D}^2 \right ] - m_{\rm D}^2} \hspace{0.05cm}.\]
- First of all, the Doppler PDF is to be determined from ${\it \Phi}_{\rm D}(f_{\rm D})$ through area normalization to $1$.
- This results in the mean Doppler shift $m_{\rm D} = {\rm E}[f_{\rm D}]$ and the standard deviation $\sigma_{\rm D}$.
$\text{Example 3:}$ The diagram is valid for a time–variant channel without direct component. Shown on the left is the $\text{Jakes spectrum}$ ${\it \Phi}_{\rm D}(f_{\rm D})$.
The Doppler spread $B_{\rm D}$ can be determined from this:
- \[f_{\rm D,\hspace{0.05cm}max} = 50\,{\rm Hz}\hspace{-0.1cm}: \hspace{-0.1cm}\hspace{0.45cm} B_{\rm D} \approx 35\,{\rm Hz} \hspace{0.05cm},\]
- \[f_{\rm D,\hspace{0.05cm}max} = 100\,{\rm Hz}\hspace{-0.1cm}: \hspace{-0.1cm}\hspace{0.2cm} B_{\rm D} \approx 70\,{\rm Hz} \hspace{0.05cm}.\]
The time correlation function $\varphi_{\rm Z}(\Delta t)$ is sketched on the right, as the Fourier transform of ${\it \Phi}_{\rm D}(f_{\rm D})$ .
This can be expressed for given boundary conditions with the Bessel function ${\rm J}_0()$ as:
- \[\varphi_{\rm Z}(\Delta t \hspace{-0.05cm} = \hspace{-0.05cm}T_{\rm D}) \hspace{-0.05cm}= \hspace{-0.05cm} {\rm J}_0(2 \pi \hspace{-0.05cm} \cdot \hspace{-0.05cm} f_{\rm D,\hspace{0.1cm}max} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\Delta t ).\]
- The correlation duration of the blue curve is $T_{\rm D} = 4.84 \ \rm ms$.
- For $f_{\rm D,\hspace{0.1cm}max} = 100\,{\rm Hz}$ the correlation duration is only half.
- In this case, it generally applies: $B_{\rm D} \cdot T_{\rm D}\approx 0.17$.
Simulation according to the GWSSUS model
The »Monte–Carlo method«, here described for the simulation of a GWSSUS mobile communication channel, is based on work by Rice [Ric44][1] and Höher [Höh90][2].
- The two–dimensional impulse response is represented by a sum of $M$ complex exponential functions. $M$ can be interpreted as the number of different paths:
- \[h(\tau,\ t)= \frac{1}{\sqrt {M}} \cdot \sum_{m=1}^{M} \alpha_m \cdot \delta (t - \tau_m) \cdot {\rm e}^{{\rm j} \hspace{0.05cm} \phi_{m} }\cdot {\rm e}^{ {\rm j} \hspace{0.05cm}2 \pi f_{{\rm D},\hspace{0.05cm} m} t} \hspace{0.05cm}. \]
- First, the delays $\tau_m$, the attenuation factors $\alpha_m$, the equally distributed phases $\phi_m$ and the Doppler frequencies $f_{{\rm D},\hspace{0.1cm} m}$ will be randomly generated according to the GWSSUS specifications. The base for the random generation of the Doppler frequencies $f_{{\rm D},\hspace{0.1cm} m}$ is the $\text{Jakes spectrum}$ ${\it \Phi}_{\rm D}(f_{\rm D})$, which, appropiately normalized, simultaneously indicates the probability density function $\rm (PDF)$ of the Doppler frequencies.
- Because of ${\it \Phi}_{\rm VD}(\tau, f_{\rm D}) = {\it \Phi}_{\rm V}(\tau) \cdot {\it \Phi}_{\rm D}(f_{\rm D})$ the delay time $\tau_m$ is independent of the Doppler frequency $f_{{\rm D},\hspace{0.1cm} m}$ for all $m$. This is valid with good approximation for terrestrial land mobile communication. For the random generation of the parameters $\alpha_m$ and $\tau_m$, which determine the delay–power-spectral density $ {\it \Phi}_{\rm V}(\tau)$ the following $\text{COST profiles}$ are available: $\rm RA$ ("Rural Area"), $\rm TU$ ("Typical Urban"), $\rm BU$ ("Bad Urban") and $\rm HT$ ("Hilly Terrain").
- The greater the number of different paths $M$ is chosen for the simulation, the better a real impulse response is approximated by the above equation. However, the higher accuracy of the simulation is at the expense of its duration. In the literature, favorable values are given for $M$ between $100$ and $600$ .
$\text{Example 4:}$ The graphic from [Hin08][3] shows a simulation result: $20 \cdot \lg \vert H(f, \hspace{0.1cm}t)\vert$ is shown as a 2D plot, where the time-variant transfer function $H(f, \hspace{0.1cm}t)$ is also referred to as $\eta_{\rm FZ}(f, \hspace{0.1cm}t)$ in this tutorial.
The simulation is based on the following parameters:
- The time variance results from a movement with $v = 3 \ \rm km/h$.
- The carrier frequency is $f_{\rm T} = 2 \ \rm GHz$.
- The maximum delay time is $\tau_{\rm max} \approx 0.4 \ \rm µ s$.
- According to the approximation we obtain the coherence bandwidth $B_{\rm K}\hspace{0.02cm}' \approx 2.5 \ \rm MHz$.
- The maximum Doppler frequency is $f_\text{D, max} \approx 5.5 \ \rm Hz$.
- The Doppler spread results in $B_{\rm D} \approx 4 \ \rm Hz$.
Exercises for the chapter
Exercise 2.5: Scatter Function
Exercise 2.5Z: Multi-Path Scenario
Exercise 2.6: Dimensions in GWSSUS
Exercise 2.7: Coherence Bandwidth
Exercise 2.7Z: Coherence Bandwidth of the LTI Two-Path Channel
Exercise 2.8: COST Delay Models
References
- ↑ Rice, S.O.: Mathematical Analysis of Random Noise. BSTJ–23, pp. 282–332 und BSTJ–24, pp. 45–156, 1945.
- ↑ Höher, P.: Empfang trelliscodierter PSK–Signale auf frequenzselektiven Mobilfunkkanälen – Entzerrung, Decodierung und Kanalschätzung. Düsseldorf: VDI–Verlag, Fortschrittsberichte, Reihe 10, Nr. 147, 1990.
- ↑ Hindelang, T.: Mobile Communications. Lecture notes. Institute for Communications Engineering. Munich: Technical University of Munich, 2008.