Difference between revisions of "Channel Coding/Soft-in Soft-Out Decoder"
| (111 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü=Iterative | + | |Untermenü=Iterative Decoding Methods |
| − | |Vorherige Seite= | + | |Vorherige Seite=Distance Characteristics and Error Probability Bounds |
| − | |Nächste Seite= | + | |Nächste Seite=The Basics of Product Codes |
}} | }} | ||
| − | == | + | == # OVERVIEW OF THE FOURTH MAIN CHAPTER # == |
<br> | <br> | ||
| − | |||
| − | + | The last main chapter of the channel coding book describes »'''iterative decoding techniques'''« as used in most of today's (2017) communication systems. This is due to the following reasons: | |
| − | + | *To approach the channel capacity, one needs very long codes. | |
| − | * | ||
| − | * | + | *But for long codes, "blockwise maximum likelihood decoding" is almost impossible. |
| − | |||
| − | + | The decoder complexity can be significantly reduced with almost the same quality if two $($or more$)$ short channel codes are linked together and the newly acquired $($soft$)$ information is exchanged between the decoders at the receiver in several steps ⇒ "iteratively". | |
| − | + | The breakthrough in the field came in the early 1990s with the invention of the "turbo codes" by [https://en.wikipedia.org/wiki/Claude_Berrou $\text{Claude Berrou}$] and shortly thereafter with the rediscovery of "low-density parity-check codes" by [https://en.wikipedia.org/wiki/David_J._C._MacKay $\text{David J. C. MacKay}$] and [https://en.wikipedia.org/wiki/Radford_M._Neal $\text{Radford M. Neal}$], after the LDPC codes developed as early as 1961 by [https://en.wikipedia.org/wiki/Robert_G._Gallager $\text{Robert G. Gallager}$] had been forgotten in the meantime. | |
| − | + | Specifically, the fourth main chapter discusses: | |
| − | + | *a comparison of »hard decision« and »soft decision«, | |
| − | * | ||
| − | * | + | *the quantification of »reliability information« by »log likelihood ratios«, |
| − | + | *the principle of symbol-wise »soft-in soft-out (SISO)« decoding, | |
| − | == Hard Decision vs. Soft Decision | + | *the definition of »a-priori L–value«, »a-posteriori L–value« and »extrinsic L–value«, |
| + | |||
| + | *the basic structure of »serially concatenated« resp. »parallel concatenated« coding systems, | ||
| + | |||
| + | *the characteristics of »product codes« and their »hard decision decoding«, | ||
| + | |||
| + | *the basic structure, decoding algorithm, and performance of »turbo codes«, | ||
| + | |||
| + | *basic information on the »low-density parity-check codes« and their applications. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Hard Decision vs. Soft Decision== | ||
<br> | <br> | ||
| − | + | To introduce the topic discussed here, let us consider the following digital transmission system with coding.<br> | |
| − | |||
| − | * | + | *In the following, all symbols are given in bipolar representation: |
| + | [[File:EN_KC_T_4_1_S1a.png|right|frame|Considered digital transmission system with coding|class=fit]] | ||
| − | + | [[File:EN_KC_T_4_1_S1b.png|right|frame|Comparison of "hard decision" and "soft decision"; for all columns of this table it is assumed:<br>'''(1)''' the information block $\underline{u} = (0,\ 1)$, bipolar representable as $(+1, \, –1)$,<br>'''(2)''' the encoded block $\underline{x} = (0,\ 1,\ 1)$ ⇒ in bipolar representation: $(+1, \, -1, \, -1)$.<br>|class=fit]] | |
| − | |||
| − | + | ||
| − | + | ::"$0$" → "$+1$", and | |
| + | ::"$1$" → "$-1$". | ||
| − | * | + | *The symbol sequence $\underline{u} = (u_1, \ u_2)$ of the digital source is assigned to the encoded sequence |
| + | :$$\underline{x} = (x_1, \ x_2, \ x_3) = (u_1, \ u_2, \ p)$$ | ||
| + | :where for the parity bit $p = u_1 ⊕ u_2$ holds ⇒ [[Channel_Coding/Examples_of_Binary_Block_Codes#Single_Parity-check_Codes| $\text{ SPC (3, 2, 2)}$]].<br> | ||
| − | * | + | *The [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_binary_input| $\text{AWGN channel}$]] changes the symbols $x_i ∈ \{+1, \ –1\}$ to real-valued output values $y_i$, for example according to $\text{channel 4}$ in the table below: |
| + | **$x_1 = +1$ ⇒ $y_1 = +0.9,$ | ||
| + | **$x_2 = -1$ ⇒ $y_1 = +0.1,$ | ||
| + | **$x_3 = -1$ ⇒ $y_1 = +0.1,$ | ||
| − | * | + | *Decoding is done according to the criterion [[Channel_Coding/Channel_Models_and_Decision_Structures#Criteria_.C2.BBMaximum-a-posteriori.C2.AB_and_.C2.BBMaximum-Likelihood.C2.AB|$\text{»block-wise maximum-likelihood«}$]] $\text{(ML)}$, distinguishing between |
| + | **"hard decision" $\rm {(ML–HD)}$, and | ||
| + | **"soft decision" $\rm {(ML–SD)}$ .<br> | ||
| − | * | + | *The given block diagram corresponds to $\rm ML–HD$. Here, only the signs of the AWGN output values ⇒ $y_{\rm HD, \ \it i} = {\rm sign}\left [y_{\rm SD, \ \it i}\right ]$ are evaluated for decoding. |
| − | + | *With "soft decision" one omits the shaded block and directly evaluates the continuous value input variables $y_{\rm SD, \ \it i}$ .<br> | |
| − | |||
| − | |||
| − | + | Thus, the four columns in the table differ only by different AWGN realizations.<br> | |
| − | = | + | {{BlaueBox|TEXT= |
| − | <br> | + | $\text{Definitions:}$ From the example table you can see: |
| − | + | *$\text{Hard Decision:}$ The sink symbol sequence $\underline{v}_{\rm HD}$ results from the "hard decided channel values" $\underline{y}_{\rm HD}$ $($blue background$)$. <br> In our example, only the constellations according to $\text{channel 1}$ and $\text{channel 2}$ are decoded without errors.<br> | |
| + | |||
| + | *$\text{Soft Decision:}$ The sink symbol sequence $\underline{v}_{\rm SD}$ results from the "soft channel output values" $\underline{y}_{\rm SD}$ $($green background$)$. <br> Now, in this example, it is also correctly decided at $\text{channel 3}$. }}<br> | ||
| + | |||
| + | The entries in the example table above are to be interpreted as follows: | ||
| + | # For ideal channel ⇒ $\text{channel 1}$ ⇒ $\underline{x} = \underline{y}_{\rm SD} = \underline{y}_{\rm HD}$ there is no difference between the (blue) conventional hard decision variant $\rm {(ML–HD)}$ and the (green) soft decision variant $\rm {(ML–SD)}$.<br> | ||
| + | # The setting according to $\text{channel 2}$ demonstrates low signal distortions. Because of $\underline{y}_{\rm HD} = \underline{x}$ $($which means that the channel does not distort the signs$)$ also $\rm ML–HD$ gives the correct result $\underline{v}_{\rm HD} = \underline{u}$.<br> | ||
| + | # At $\text{channel 3}$ there is $\underline{y}_{\rm HD} ≠ \underline{x}$ and there is also no ${\rm SPC} \ (3, 2)$ assignment $\underline{u}$ ⇒ $\underline{y}_{\rm HD}$. The maximum Likelihood decoder reports here by outputting $\underline{v}_{\rm HD} = \rm (E, \ E)$ that it failed in decoding this block. "$\rm E$" stands for an [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Erasure_Channel_.E2.80.93_BEC|$\text{Erasure}$]] .<br> | ||
| + | # Also the soft decision decoder recognizes that decoding based on the signs does not work. Based on the $\underline{y}_{\rm SD}$ values, however, it recognizes that with high probability the second bit has been falsified and decides to use the correct symbol sequence $\underline{v}_{\rm SD} = (+1, \, -1) = \underline{u}$.<br> | ||
| + | # In $\text{channel 4}$, both the signs of bit 2 and bit 3 are changed by the AWGN channel, leading to the result $\underline{v}_{\rm HD} = (+1, +1) ≠ \underline{u}(+1, \, -1)$ ⇒ a block error and a bit error at the same time. Also the soft decision decoder gives the same wrong result here.<br><br> | ||
| − | + | The decoding variant $\rm ML–SD$ also offers the advantage over $\rm ML–HD$ that it is relatively easy to assign a reliability value to each decoding result $($but in the above table this is not specified$)$. This reliability value would | |
| + | *have its maximum value for $\text{channel 1}$ ,<br> | ||
| − | + | *be significantly smaller for $\text{channel 2}$ ,<br> | |
| − | + | *be close to zero for $\text{channel 3}$ and $\text{channel 4}$.<br> | |
| − | + | == Reliability information - Log likelihood ratio== | |
| + | <br> | ||
| + | Let be $x ∈ \{+1, \, -1\}$ a binary random variable with probabilities ${\rm Pr}(x = +1)$ and ${\rm Pr}(x = \, -1)$. For coding theory, it proves convenient in terms of computation times to use the natural logarithm of the quotient instead of the probabilities ${\rm Pr}(x = ±1)$ .<br> | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ The <b>log likelihood ratio</b> $\rm (LLR)$ of the random variable $x ∈ \{+1, \, -1\}$ is: | ||
| − | + | ::<math>L(x)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(x = +1)}{ {\rm Pr}(x = -1)}\hspace{0.05cm}.</math> | |
| − | + | *For unipolar representation $(+1 → 0$ and $-1 → 1)$ applies accordingly with $\xi ∈ \{0, \, 1\}$: | |
| − | * | ||
| − | + | ::<math>L(\xi)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(\xi = 0)}{ {\rm Pr}(\xi = 1)}\hspace{0.05cm}.</math>}}<br> | |
| − | + | [[File:P ID2975 KC T 4 1 S2a v1.png|right|frame|Probability and log likelihood ratio|class=fit]] | |
| − | [[File:P | ||
| − | + | The table gives the nonlinear relationship between ${\rm Pr}(x = ±1)$ and $L(x)$. Replacing ${\rm Pr}(x = +1)$ with ${\rm Pr}(\xi = 0)$, the middle row gives the $L$–value of the unipolar random variable $\xi$.<br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | You can see: | |
| + | #The more likely random value of $x ∈ \{+1, \, -1\}$ is given by the <b>sign</b> ⇒ ${\rm sign} \ L(x)$.<br> | ||
| + | #In contrast, the <b>absolute value</b> ⇒ $|L(x)|$ indicates the reliability for the result "${\rm sign}(L(x))$".<br><br> | ||
| − | :<math>L(y | + | {{GraueBox|TEXT= |
| − | {\rm ln} \hspace{0.15cm} \frac{0. | + | [[File:P ID2976 KC T 4 1 S2b v2.png|right|frame|Given BSC model]] |
| − | + | $\text{Example 1:}$ We consider the outlined [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC| $\text{BSC model}$]] with bipolar representation. | |
| + | *With the falsification probability $\varepsilon = 0.1$ and the two random variables $x ∈ \{+1, \, -1\}$ and $y ∈ \{+1, \, -1\}$ at the input and output of the channel: | ||
| + | ::<math>L(y\hspace{0.05cm}\vert\hspace{0.05cm}x) = | ||
| + | {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(y\hspace{0.05cm}\vert\hspace{0.05cm}x = +1) }{ {\rm Pr}(y\hspace{0.05cm}\vert\hspace{0.05cm}x = -1)} = | ||
| + | \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} \big[(1 - \varepsilon)/\varepsilon \big]\\ | ||
| + | {\rm ln} \hspace{0.15cm}\big [\varepsilon/(1 - \varepsilon)\big] \end{array} \right.\quad | ||
| + | \begin{array}{*{1}c} {\rm for} \hspace{0.15cm} y = +1, | ||
| + | \\ {\rm for} \hspace{0.15cm} y = -1. \\ \end{array}</math> | ||
| − | + | *For example, $\varepsilon = 0.1$ results in the following numerical values $($compare the upper table$)$: | |
| + | ::<math>L(y = +1\hspace{0.05cm}\vert\hspace{0.05cm}x) = | ||
| + | {\rm ln} \hspace{0.15cm} \frac{0.9}{0.1} = +2.197\hspace{0.05cm}, \hspace{0.8cm} | ||
| + | L(y = -1\hspace{0.05cm}\vert\hspace{0.05cm}x) = -2.197\hspace{0.05cm}.</math> | ||
| − | == | + | *This example shows that the so-called »$\text{LLR algebra}$« can also be applied to conditional probabilities. In [[Aufgaben:Exercise_4.1Z:_Log_Likelihood_Ratio_at_the_BEC_Model|"Exercise 4.1Z"]], the BEC–model is described in a similar way.}}<br> |
| − | + | ||
| − | + | {{GraueBox|TEXT= | |
| + | [[File:EN_KC_T_4_1_S2c.png|right|frame|Conditional AWGN probability density functions|class=fit]] | ||
| + | $\text{Example 2:}$ | ||
| + | In another example, we consider the [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_binary_input|$\rm AWGN$ ]] channel with the conditional probability density functions | ||
| − | :<math>f_{y \hspace{0.03cm} | + | ::<math>f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 )\hspace{-0.1cm} = \hspace{-0.1cm} |
\frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y-1)^2}/(2\sigma^2) } \hspace{0.05cm},</math> | \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y-1)^2}/(2\sigma^2) } \hspace{0.05cm},</math> | ||
| − | :<math>f_{y \hspace{0.03cm} | + | ::<math>f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=-1 )\hspace{-0.1cm} = \hspace{-0.1cm} |
\frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y+1)^2}/(2\sigma^2) } \hspace{0.05cm}.</math> | \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y+1)^2}/(2\sigma^2) } \hspace{0.05cm}.</math> | ||
| − | In | + | ⇒ In the graph, two exemplary Gaussian functions are shown as blue and red curves, respectively. |
| − | + | *The total probability density function $\rm (PDF)$ of the output signal $y$ is obtained from the (equally) weighted sum: | |
| − | + | ::<math>f_{y } \hspace{0.05cm} (y ) = 1/2 \cdot \big [ f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 ) \hspace{0.1cm} + \hspace{0.1cm} | |
| − | + | f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert \hspace{0.05cm}x=-1 ) | |
| − | :<math>f_{y } \hspace{0.05cm} (y ) = 1/2 \cdot \big [ f_{y \hspace{0.03cm} | ||
| − | f_{y \hspace{0.03cm} | ||
\big ] | \big ] | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | * We now calculate the probability that the received value $y$ lies in a (very) narrow interval of width $\it \Delta$ around $y_0 = 0.25$. One obtains approximately | |
| − | :<math>{\rm Pr} ( | + | ::<math>{\rm Pr} (\vert y - y_0\vert \le{\it \Delta}/2 \hspace{0.05cm} |
| − | \Big | + | \Big \vert \hspace{0.05cm}x=+1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} |
\frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2) } \hspace{0.05cm},</math> | \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2) } \hspace{0.05cm},</math> | ||
| − | :<math>{\rm Pr} ( | + | ::<math>{\rm Pr} (\vert y - y_0\vert \le {\it \Delta}/2 \hspace{0.05cm} |
| − | \Big | + | \Big \vert \hspace{0.05cm}x=-1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} |
\frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2) } \hspace{0.05cm}.</math> | \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2) } \hspace{0.05cm}.</math> | ||
| − | + | :The slightly larger vertical lines denote the conditions, the smaller ones the absolute value.<br> | |
| − | + | *The log likelihood ratio $\rm (LLR)$ of the conditional probability in the forward direction $($meaning: output $y$ for a given input $x)$ is thus obtained as the logarithm of the quotient of both expressions: | |
| − | :<math>L(y = y_0\hspace{0.05cm} | + | ::<math>L(y = y_0\hspace{0.05cm}\vert\hspace{0.05cm}x) = |
{\rm ln} \hspace{0.15cm} \left [ \frac{{\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2)}}{{\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2)}} \right ] = | {\rm ln} \hspace{0.15cm} \left [ \frac{{\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2)}}{{\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2)}} \right ] = | ||
| − | {\rm ln} \left [ {\rm e} ^{ - [ {(y_0-1)^2}+{(y_0+1)^2}]/(2\sigma^2)} \right ] | + | {\rm ln} \left [ {\rm e} ^{ - [ {(y_0-1)^2}+{(y_0+1)^2}]/(2\sigma^2)} \right ] = \frac{(y_0+1)^2-(y_0-1)^2}{2\cdot \sigma^2} = \frac{2 \cdot y_0}{\sigma^2}\hspace{0.05cm}. </math> |
| − | |||
| − | + | *If we now replace the auxiliary $y_0$ with the general random $y$ at the AWGN output, the final result is: | |
| − | :<math>L(y \hspace{0.05cm} | + | ::<math>L(y \hspace{0.05cm}\vert\hspace{0.05cm}x) = {2 \cdot y}/{\sigma^2} =K_{\rm L} \cdot y\hspace{0.05cm}. </math> |
| − | + | :Here $K_{\rm L} = 2/\sigma^2$ is a constant that depends solely on the standard deviation of the Gaussian noise component.}}<br> | |
| − | == | + | == Bit-wise soft-in soft-out decoding == |
<br> | <br> | ||
| − | + | We now assume an $(n, \ k)$ block code where the code word $\underline{x} = (x_1, \ \text{...} \ , \ x_n)$ is falsified by the channel into the received word $\underline{y} = (y_1, \ \text{...} \ , \ y_n)$. | |
| + | [[File:EN_KC_T_4_1_S4.png|right|frame|Model of bit-wise soft-in soft-out decoding|class=fit]] | ||
| + | |||
| + | *For long codes, a "maximum-a-posteriori block-level decision" $($for short: <b>[[Channel_Coding/Channel_Models_and_Decision_Structures#Criteria_.C2.BBMaximum-a-posteriori.C2.AB_and_.C2.BBMaximum-Likelihood.C2.AB|$\text{ block-wise MAP}$]]</b> – very elaborate. | ||
| + | |||
| + | *One would have to find among the $2^k $ allowable code words $\underline{x}_j ∈ \mathcal{C}$ the one with the greatest a-posteriori probability $\rm (APP)$. | ||
| + | |||
| + | *The code word to output $\underline{z}$ in this case would be | ||
| + | :$$\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}j} \hspace{0.03cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}j} |\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.$$ | ||
| + | <br clear=all> | ||
| + | A second possibility is decoding on bit level. The represented bit-wise $\text{soft-in soft out decoder}$ has the task to decode all code word bits $x_i ∈ \{0, \, 1\}$ according to maximum a-posteriori probability ${\rm Pr}(x_i | \underline{y})$. With the control variable $i = 1, \text{...} , \ n$ holds in this case: | ||
| − | + | *The corresponding log likelihood ratio for the $i$th code bit is: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
::<math>L_{\rm APP} (i) = L(x_i\hspace{0.05cm}|\hspace{0.05cm}\underline{y}) = | ::<math>L_{\rm APP} (i) = L(x_i\hspace{0.05cm}|\hspace{0.05cm}\underline{y}) = | ||
{\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x_i = 0\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}{{\rm Pr}(x_i = 1\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}\hspace{0.05cm} . </math> | {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x_i = 0\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}{{\rm Pr}(x_i = 1\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}\hspace{0.05cm} . </math> | ||
| − | * | + | *The decoder works iteratively. At initialization $($indicated in the diagram by the parameter $I = 0)$ is $L_{\rm APP}(i) = L_{\rm K}(i)$, where the channel $($German: "Kanal" ⇒ "K"$)$ log likelihood ratio $L_{\rm K}(i)$ is given by the received value $y_i$.<br> |
| − | * | + | *In addition, the extrinsic log likelihood ratio $L_{\rm E}(i)$ is calculated, which quantifies the total information provided by all other bits $(j ≠ i)$ due to the code properties about the considered $i$th bit.<br> |
| − | * | + | *At the next iteration $(I = 1)$ $L_{\rm E}(i)$ is taken into account in the computation of $L_{\rm APP}(i)$ as a-priori information $L_{\rm A}(i)$. Thus, for the new a-posteriori log likelihood ratio in iteration $I + 1$ holds: |
::<math>L_{\hspace{0.1cm}\rm APP}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm A}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm E}^{(I)} (i)\hspace{0.05cm} . </math> | ::<math>L_{\hspace{0.1cm}\rm APP}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm A}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm E}^{(I)} (i)\hspace{0.05cm} . </math> | ||
| − | * | + | *The iterations continue until all absolute values $|L_{\rm APP}(i)|$ are greater than a given value. The most likely code word $\underline{z}$ is then obtained from the signs of all $L_{\rm APP}(i)$, with $i = 1, \ \text{...} , \ n$.<br> |
| − | * | + | *For a [[Channel_Coding/General_Description_of_Linear_Block_Codes#Systematic_Codes| $\text{systematic code}$]] the first $k$ bits of $\underline{z}$ indicate the information word $\underline{\upsilon}$ being searched for, which will most likely match the message $\underline{u}$ being sent.<br><br> |
| − | + | This SISO decoder descriptione from [Bos99]<ref name='Bos99'>Bossert, M.: Channel Coding for Telecommunications. Chichester: Wiley, 1999. ISBN: 978-0-471-98277-7.</ref> is intended at this point primarily to clarify the different $L$–values. One recognizes the large potential of the bit-wise decoding only in connection with [[Channel_Coding/Soft-in_Soft-Out_Decoder#Basic_structure_of_concatenated_coding_systems|$\text{concatenated coding systems}$]].<br> | |
| − | == | + | == Calculation of extrinsic log likelihood ratios == |
<br> | <br> | ||
| − | + | The difficulty in bit-wise $($or symbol-wise$)$ iterative decoding is generally the provision of the extrinsic log likelihood ratios $L_{\rm E}(i)$. For a code of length $n$, the control variable is $i = 1, \ \text{...} , \ n$.<br> | |
| − | {{Definition} | + | {{BlaueBox|TEXT= |
| + | $\text{Definition:}$ The <b> extrinsic log likelihood ratio</b> is a measure of the information that the other symbols $(j ≠ i)$ of the code word provide about the $i$–th encoded symbol, expressed as a log likelihood ratio. We denote this characteristic value by $L_{\rm E}(i)$.}} | ||
| − | |||
| − | + | We now calculate the extrinsic log likelihood ratios $L_{\rm E}(i)$ for two example codes.<br> | |
| − | + | $\text{(A) Repetition Code}$ ⇒ ${\rm RC} \ (n, 1, n)$</b><br> | |
| − | :<math>L_{\rm E}(i) = \hspace{0.05cm}\sum_{j \ne i} \hspace{0.1cm} L_j | + | A repetition code $\rm (RC)$ is characterized by the fact that all $n$ encoded symbols $x_i ∈ \{0, \, 1\}$ are identical. |
| − | \hspace{0.3cm}{\rm | + | |
| + | *Here, the extrinsic log likelihood ratio for the $i$–th symbol is very easy to specify: | ||
| + | |||
| + | ::<math>L_{\rm E}(i) = \hspace{0.05cm}\sum_{j \ne i} \hspace{0.1cm} L_j | ||
| + | \hspace{0.3cm}{\rm with}\hspace{0.3cm}L_j = L_{\rm APP}(j) | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| + | *If the sum over all $L_{j ≠ i}$ is positive ⇒ this implies from the point of view of the other log likelihood ratio values a preference for the decision $x_i = 0$. | ||
| + | |||
| + | *On the other hand, if the sum is negative ⇒ $x_i = 1$ is more likely. | ||
| + | |||
| + | *$L_{\rm E}(i) = 0$ does not allow a prediction.<br> | ||
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 5:}$ We consider the decoding of the repetition code $\text{RC (4, 1,4)}$. Thereby, we make three different assumptions for the log likelihood ratio $ \underline{L}_{\rm APP}^{(I=0)}=\underline{L}_{\rm K}.$ | ||
| + | |||
| + | [[File:EN_KC_T_4_1_S3a.png|right|frame|Decoding example $\rm (5a)$ for the ${\rm RC} \ (4, 1, 4)$|class=fit]] | ||
| + | $\text{Decoding example (5a):}$ | ||
| + | :$$\underline{L}_{\rm APP}^{(I=0)} = (+1, -1, +3, -1)\text{:}$$ | ||
| + | ::$$L_{\rm E}(1) = -1+3-1 = +1\hspace{0.05cm},$$ | ||
| + | ::$$L_{\rm E}(2) = +1+3-1 = +3\hspace{0.05cm},$$ | ||
| + | ::$$L_{\rm E}(3) = +1-1 -1= -1\hspace{0.05cm},$$ | ||
| + | ::$$L_{\rm E}(4) = +1-1 +3 = +3\hspace{0.05cm}$$ | ||
| + | :$$\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm E}^{(I=0)}= (+1, +3, -1, +3) | ||
| + | \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm APP}^{(I=1)}=\underline{L}_{\rm APP}^{(I=0)}+ \underline{L}_{\rm E}^{(I=0)}= (+2, +2, +2, +2)$$ | ||
| + | *At the beginning $(I=0)$ the positive $L_{\rm E}$ values indicate $x_1 = x_2 = x_4 = 0$ while $x_3 =1$ is more likely $($because of negative $L_{\rm E})$ . | ||
| + | |||
| + | *Already after one iteration $(I=1)$ all $L_{\rm APP}$ values are positive ⇒ the information bit is decoded as $u = 0$. | ||
| + | |||
| + | *Further iterations yield nothing.<br> | ||
| + | |||
| + | |||
| + | $\text{Decoding example (5b):}$ | ||
| + | [[File:EN_KC_T_4_1_S3ab.png|right|frame|Decoding example $\rm (5b)$ for the ${\rm RC} \ (4, 1, 4)$]] | ||
| + | |||
| + | :$$\underline{L}_{\rm APP}^{(I=0)} = (+1, +1, -4, +1)\text{:}$$ | ||
| + | :$$\underline{L}_{\rm E}^{(I=0)} = \ (-2, -2, +3, -2)$$ | ||
| + | |||
| + | *Although three signs were wrong at the beginning, after two iterations all $L_{\rm APP}$ values are negative. | ||
| − | + | *The information bit is decoded as $u = 1$. | |
| − | |||
| − | |||
| − | |||
| − | + | [[File:EN_KC_T_4_1_S3c.png|right|frame|Decoding example $\rm (5c)$ for the ${\rm RC} \ (4, 1, 4)$]]<br> | |
| + | $\text{Decoding example (5c):}$ | ||
| + | :$$\underline{L}_{\rm APP}^{(I=0)} = (+1, +1, -3, +1)\text{:}$$ | ||
| + | :$$\underline{L}_{\rm E}^{(I=0)} = (-1, -1, +3, -1)$$ | ||
| − | + | *All $L_{\rm APP}$ values are zero already after one iteration. | |
| − | * | + | *The information bit cannot be decoded, although the initial situation was not much worse than with $\rm (5b)$. |
| + | |||
| + | *Further iterations bring nothing here.<br>}} | ||
| − | |||
| − | + | ||
| + | $\text{(B) Single parity–check code}$ ⇒ ${\rm SPC} \ (n, \ n \, -1, \ 2)$ | ||
<br> | <br> | ||
| − | |||
| − | |||
| − | + | For each single parity–check code, the number of "ones" in each code word is even. Or, put another way: For each code word $\underline{x}$ the [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding|$\text{Hamming weight}$]] $w_{\rm H}(\underline{x})$ is even.<br> | |
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ Let the code word $\underline{x}^{(–i)}$ contain all symbols except $x_i$ ⇒ vector of length $n–1$. Thus, the "extrinsic log likelihood ratio" will be with respect to the $i$–th symbol, when $\underline{x}$ has been received: | ||
| − | :<math>L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm | + | ::<math>L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} \vert\hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} \vert \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *As will be shown in the [[Aufgaben:Aufgabe_4.4:_Extrinsische_L–Werte_beim_SPC|"Exercise 4.4"]], it is also possible to write for this: | |
| + | |||
| + | ::<math>L_{\rm E}(i) = 2 \cdot {\rm tanh}^{-1} \hspace{0.1cm} \left [ \prod\limits_{j \ne i}^{n} \hspace{0.15cm}{\rm tanh}(L_j/2) \right ] | ||
| + | \hspace{0.3cm}{\rm with}\hspace{0.3cm}L_j = L_{\rm APP}(j) | ||
| + | \hspace{0.05cm}.</math>}} | ||
| − | |||
| − | |||
| − | |||
| − | {{ | + | {{GraueBox|TEXT= |
| + | $\text{Example 6:}$ We assume a "Single parity–check code" with $n = 3, \ k = 2$ ⇒ briefly ${\rm SPC} \ (3, \ 2, \ 2)$. | ||
| + | |||
| + | *The $2^k = 4$ valid code words $\underline{x} = \{x_1,\ x_2,\ x_3\}$ are for bipolar description ⇒ $x_i ∈ \{±1\}$: | ||
| + | [[File:EN_KC_T_4_1_S3e.png|right|frame|Decoding example for the ${\rm SPC} \ (3, 2, 2)$|class=fit]] | ||
| − | : | + | :$$ \underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{-0.05cm}, $$ |
| − | \underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, | + | :$$\underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, $$ |
| − | \underline{x}_2 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} +1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, | + | :$$\underline{x}_2 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} +1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, $$ |
| − | \underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} +1)\hspace{-0.05cm}. | + | :$$\underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} +1)\hspace{-0.05cm}. $$ |
| − | + | :So, the product $x_1 \cdot x_2 \cdot x_3$ is always positive.<br> | |
| − | + | *The table shows the decoding process for $\underline{L}_{\rm APP} = (+2.0, +0.4, \, –1.6)$. | |
| − | + | *The hard decision according to the signs of $L_{\rm APP}(i)$ would yield here $(+1, +1, \, -1)$ ⇒ no valid code word of ${\rm SP}(3, \ 2, \ 2)$.<br> | |
| − | + | *On the right side of the table, the corresponding extrinsic log likelihood ratios are entered:<br> | |
| − | :<math>L_{\rm E}(1) | + | ::<math>L_{\rm E}(1) = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} |
\left [ {\rm tanh} (0.2) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.131\hspace{0.05cm}, </math> | \left [ {\rm tanh} (0.2) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.131\hspace{0.05cm}, </math> | ||
| − | :<math>L_{\rm E}(2) | + | ::<math>L_{\rm E}(2) =2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} |
\left [ {\rm tanh} (1.0) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.518\hspace{0.05cm}, </math> | \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.518\hspace{0.05cm}, </math> | ||
| − | :<math>L_{\rm E}(3) | + | ::<math>L_{\rm E}(3) =2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} |
\left [ {\rm tanh} (1.0) \cdot {\rm tanh} (0.2)\hspace{0.05cm}\right ] = +0.151\hspace{0.05cm}.</math> | \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (0.2)\hspace{0.05cm}\right ] = +0.151\hspace{0.05cm}.</math> | ||
| − | + | The second equation can be interpreted as follows: | |
| − | + | # $L_{\rm APP}(1) = +2.0$ and $L_{\rm APP}(3) = \, -1.6$ state that the first bit is more likely to be "$+1$" than "$-1$" and the third bit is more likely to be "$-1"$ than "$+1$". | |
| + | #The reliability $($the amount$)$ is slightly greater for the first bit than for the third.<br> | ||
| + | #The extrinsic information $L_{\rm E}(2) = \, -0.518$ considers only the information of bit 1 and bit 3 about bit 2. | ||
| + | #From their point of view, the second bit is "$-1$" with reliability $0.518$.<br> | ||
| + | #The log likelihood ratio $L_{\rm APP}^{I=0}(2) = +0.4$ derived from the received value $y_2$ has suggested "$+1$" for the second bit. | ||
| + | #But the discrepancy is resolved here already in the iteration $I = 1$. The decision falls here for the code word $\underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm},$. | ||
| + | #For $0.518 < L_{\rm APP}(2) < 1.6$ the result $\underline{x}_1$ would only be available after several iterations. For $L_{\rm APP}(2) > 1.6$ on the other hand, the decoder returns $\underline{x}_0$.}}<br> | ||
| − | + | == BCJR decoding: Forward-backward algorithm == | |
| + | <br> | ||
| + | An example of iterative decoding of convolutional codes is the »<b>BCJR algorithm</b>«, named after its inventors L. R. Bahl, J. Cocke, F. Jelinek, and J. Raviv ⇒ [BCJR74]<ref name='BCJR74'>Bahl, L.R.; Cocke, J.; Jelinek, F.; Raviv, J.: Optimal Decoding of Linear Codes for Minimizing Symbol Error Rate. In: IEEE Transactions on Information Theory, Vol. IT-20, pp. 284-287, 1974.</ref>. The algorithm has many parallels to the seven-year older Viterbi decoding, but also some significant differences: | ||
| + | *While Viterbi estimates the total sequence ⇒ [[Channel_Coding/Channel_Models_and_Decision_Structures#Definitions_of_the_different_optimal_receivers|$\text{block–wise maximum likelihood}$]], the BCJR– Algorithm minimizes the bit error probability ⇒ [[Channel_Coding/Channel_Models_and_Decision_Structures#Definitions_of_the_different_optimal_receivers|$\text{bit–wise MAP}$]].<br> | ||
| − | * | + | *The Viterbi algorithm $($in its original form$)$ cannot process soft information. In contrast, the BCJR algorithm specifies a reliability value for each individual bit at each iteration, which is taken into account in subsequent iterations.<br> |
| − | |||
| − | + | The figure is intended to illustrate $($in an almost inadmissibly simplified way$)$ the different approach of Viterbi and BCJR algorithm. This is based on a convolutional code with memory $m = 1$ and length $L = 4$ ⇒ total length $($with termination$)$ $L' = 5$. | |
| − | + | [[File:EN_KC_T_4_1_S5.png|right|frame|Comparison of Viterbi and BCJR algorithm|class=fit]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[ | + | *Viterbi searches and finds the most likely path from ${\it \Gamma}_0(S_0)$ to ${\it \Gamma}_5(S_0)$, namely $S_0 → S_1 → S_0 → S_0 → S_1→ S_0 $. We refer to the sample solution to [[Aufgaben:Exercise_3.09Z:_Viterbi_Algorithm_again|"Exercise 3.9Z"]].<br> |
| − | + | *The sketch for the BCJR algorithm illustrates the extraction of the extrinsic L–value for the third symbol ⇒ $L_{\rm E}(3)$. The relevant area in the trellis is shaded: | |
| − | |||
| − | + | * Working through the trellis diagram in the forward direction, one obtains in the same way as Viterbi the metrics $\alpha_1, \ \alpha_2, \ \text{...}\hspace{0.05cm} , \ \alpha_5$. To calculate $L_{\rm E}(3)$ one needs from this $\alpha_2$.<br> | |
| − | * | ||
| − | * | + | * Then we traverse the trellis diagram backwards $($i.e. from right to left$)$ and thus obtain the metrics $\beta_4, \ \beta_3, \ \text{...}\hspace{0.05cm} , \ \beta_0$ corresponding to the sketch below.<br> |
| − | * | + | * The extrinsic log likelihood ratio $L_{\rm E}(3)$ is obtained from the forward direction metric $\alpha_2$ and the backward direction metric $\beta_3$ and the a-priori information $\gamma_3$ about the symbol $i = 3$.<br> |
| − | == | + | == Basic structure of concatenated coding systems == |
<br> | <br> | ||
| − | + | The most important communication systems of the last years use two different channel codes. One speaks then of »'''concatenated codes'''«. Even with relatively short component codes $\mathcal{C}_1$ and $\mathcal{C}_2$ the concatenated code $\mathcal{C}$ results in a sufficiently large code word length $n$, which is known to be necessary to approach the channel capacity.<br> | |
| − | + | To begin with, here are a few examples from mobile communications: | |
| − | * | + | *In [[Examples_of_Communication_Systems/General_Description_of_GSM#.23_OVERVIEW_OF_THE_THIRD_MAIN_CHAPTER_.23|$\rm GSM$]] $($"Global System for Mobile Communications", the second generation of mobile communication systems$)$, the data bit rate is first increased from $9. 6 \ \rm kbit/s$ to $12 \ \rm kbit/s$ in order to enable error detection in circuit-switched networks as well. This is followed by a punctured convolutional code with the output bit rate $22.8 \ \rm kbit/s$. The total code rate is thus about $0.421$. |
| − | * | + | *In the 3G cellular system [[Examples_of_Communication_Systems/General_Description_of_UMTS#.23_OVERVIEW_OF_THE_FOURTH_MAIN_CHAPTER_.23|$\rm UMTS$]] $($"Universal Mobile Telecommunications System"), depending on the boundary conditions $($good/bad channel, few/many subscribers in the cell$)$ one uses a [[Examples_of_Communication_Systems/General_Description_of_GSM#.23_OVERVIEW_OF_THE_THIRD_MAIN_CHAPTER_.23|$\text{convolutional code}$]] or a [[Channel_Coding/The_Basics_of_Turbo_Codes#Basic_structure_of_a_turbo_code|$\text{turbo code}$]] $($by this one understands per se the concatenation of two convolutional encoders$)$. |
| − | [[ | + | *In 4G mobile communication systems [[Examples_of_Communication_Systems/General_Description_of_UMTS#.23_OVERVIEW_OF_THE_FOURTH_MAIN_CHAPTER_.23|$\rm LTE$]] $($"Long Term Evolution"$)$, a convolutional code is used for short control signals, turbo code for the longer payload data.<br> |
| − | |||
| − | |||
| − | |||
| − | + | The graph shows the basic structure of a parallel concatenated coding system. All vectors consist of $n$ elements: | |
| + | :$$\underline{L} = (L(1), \ \text{...}\hspace{0.05cm} , \ L(n)).$$ | ||
| + | [[File:EN_KC_T_4_1_S6.png|right|frame|Parallel concatenated codes|class=fit]] | ||
| + | So the calculation of all L–values is done on symbol level. Not shown here is the [[Channel_Coding/The_Basics_of_Turbo_Codes#Second_requirement_for_turbo_codes:_Interleaving| $\rm interleaver$]], which is mandatory e.g. for turbo codes. | ||
| + | # The sequences $\underline{x}_1$ and $\underline{x}_2$ are combined to form the vector $\underline{x}$ for joint transmission over the channel by a multiplexer. | ||
| + | # At the receiver, the sequence $\underline{y}$ is again decomposed into the parts $\underline{y}_1$ and $\underline{y}_2$. From this the channel L–values $\underline{L}_{\rm K,\hspace{0.05cm}1} $ and $\underline{L}_{\rm K,\hspace{0.05cm}2}$ are formed.<br> | ||
| + | # The symbol-wise decoder determines the extrinsic log likelihood ratios $\underline{L}_{\rm E,\hspace{0.05cm} 1}$ and $\underline{L}_{\rm E,\hspace{0.05cm} 2}$, which are also the a-priori information $\underline{L}_{\rm A,\hspace{0.05cm} 2}$ and $\underline{L}_{\rm A,\hspace{0.05cm} 1}$ for the other decoder. <br> | ||
| + | # After a sufficient number of iterations $($i.e. when a termination criterion is met$)$, the vector $\underline{L}_{\rm APP}$ of a-posteriori values is available at the decoder output. | ||
| + | # In the example, the value in the upper branch is taken arbitrarily. | ||
| + | # However, the lower log likelihood ratio would also be possible.<br><br> | ||
| − | + | The above model also applies in particular to the decoding of turbo codes according to the chapter [[Channel_Coding/The_Basics_of_Turbo_Codes#Basic_structure_of_a_turbo_code|"Basic structure of a turbo code"]].<br> | |
| − | == | + | == Exercises for the chapter == |
<br> | <br> | ||
| − | [[Aufgaben:4.1 | + | [[Aufgaben:Exercise_4.1:_Log_Likelihood_Ratio|Exercise 4.1: Log Likelihood Ratio]] |
| + | |||
| + | [[Aufgaben:Exercise_4.1Z:_Log_Likelihood_Ratio_at_the_BEC_Model|Exercise 4.1Z: Log Likelihood Ratio at the BEC Model]] | ||
| + | |||
| + | [[Aufgaben:Exercise_4.2:_Channel_Log_Likelihood_Ratio_at_AWGN|Exercise 4.2: Channel Log Likelihood Ratio at AWGN]] | ||
| − | [[ | + | [[Aufgaben:Exercise_4.3:_Iterative_Decoding_at_the_BSC|Exercise 4.3: Iterative Decoding at the BSC]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.3Z:_Conversions_of_L-value_and_S-value|Exercise 4.3Z: Conversions of L-value and S-value]] |
| − | [[Aufgaben:4 | + | [[Aufgaben:Exercise_4.4:_Extrinsic_L-values_at_SPC|Exercise 4.4: Extrinsic L-values at SPC]] |
| − | [[ | + | [[Aufgaben:Exercise_4.4Z:_Supplement_to_Exercise_4.4|Exercise 4.4Z: Supplement to Exercise 4.4]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.5:_On_the_Extrinsic_L-values_again|Exercise 4.5: On the Extrinsic L-values again]] |
| − | [[ | + | [[Aufgaben:Exercise_4.5Z:_Tangent_Hyperbolic_and_Inverse|Exercise 4.5Z: Tangent Hyperbolic and Inverse]] |
| − | == | + | ==References== |
<references/> | <references/> | ||
{{Display}} | {{Display}} | ||
Latest revision as of 17:21, 12 January 2023
Contents
- 1 # OVERVIEW OF THE FOURTH MAIN CHAPTER #
- 2 Hard Decision vs. Soft Decision
- 3 Reliability information - Log likelihood ratio
- 4 Bit-wise soft-in soft-out decoding
- 5 Calculation of extrinsic log likelihood ratios
- 6 BCJR decoding: Forward-backward algorithm
- 7 Basic structure of concatenated coding systems
- 8 Exercises for the chapter
- 9 References
# OVERVIEW OF THE FOURTH MAIN CHAPTER #
The last main chapter of the channel coding book describes »iterative decoding techniques« as used in most of today's (2017) communication systems. This is due to the following reasons:
- To approach the channel capacity, one needs very long codes.
- But for long codes, "blockwise maximum likelihood decoding" is almost impossible.
The decoder complexity can be significantly reduced with almost the same quality if two $($or more$)$ short channel codes are linked together and the newly acquired $($soft$)$ information is exchanged between the decoders at the receiver in several steps ⇒ "iteratively".
The breakthrough in the field came in the early 1990s with the invention of the "turbo codes" by $\text{Claude Berrou}$ and shortly thereafter with the rediscovery of "low-density parity-check codes" by $\text{David J. C. MacKay}$ and $\text{Radford M. Neal}$, after the LDPC codes developed as early as 1961 by $\text{Robert G. Gallager}$ had been forgotten in the meantime.
Specifically, the fourth main chapter discusses:
- a comparison of »hard decision« and »soft decision«,
- the quantification of »reliability information« by »log likelihood ratios«,
- the principle of symbol-wise »soft-in soft-out (SISO)« decoding,
- the definition of »a-priori L–value«, »a-posteriori L–value« and »extrinsic L–value«,
- the basic structure of »serially concatenated« resp. »parallel concatenated« coding systems,
- the characteristics of »product codes« and their »hard decision decoding«,
- the basic structure, decoding algorithm, and performance of »turbo codes«,
- basic information on the »low-density parity-check codes« and their applications.
Hard Decision vs. Soft Decision
To introduce the topic discussed here, let us consider the following digital transmission system with coding.
- In the following, all symbols are given in bipolar representation:
- "$0$" → "$+1$", and
- "$1$" → "$-1$".
- The symbol sequence $\underline{u} = (u_1, \ u_2)$ of the digital source is assigned to the encoded sequence
- $$\underline{x} = (x_1, \ x_2, \ x_3) = (u_1, \ u_2, \ p)$$
- where for the parity bit $p = u_1 ⊕ u_2$ holds ⇒ $\text{ SPC (3, 2, 2)}$.
- The $\text{AWGN channel}$ changes the symbols $x_i ∈ \{+1, \ –1\}$ to real-valued output values $y_i$, for example according to $\text{channel 4}$ in the table below:
- $x_1 = +1$ ⇒ $y_1 = +0.9,$
- $x_2 = -1$ ⇒ $y_1 = +0.1,$
- $x_3 = -1$ ⇒ $y_1 = +0.1,$
- Decoding is done according to the criterion $\text{»block-wise maximum-likelihood«}$ $\text{(ML)}$, distinguishing between
- "hard decision" $\rm {(ML–HD)}$, and
- "soft decision" $\rm {(ML–SD)}$ .
- The given block diagram corresponds to $\rm ML–HD$. Here, only the signs of the AWGN output values ⇒ $y_{\rm HD, \ \it i} = {\rm sign}\left [y_{\rm SD, \ \it i}\right ]$ are evaluated for decoding.
- With "soft decision" one omits the shaded block and directly evaluates the continuous value input variables $y_{\rm SD, \ \it i}$ .
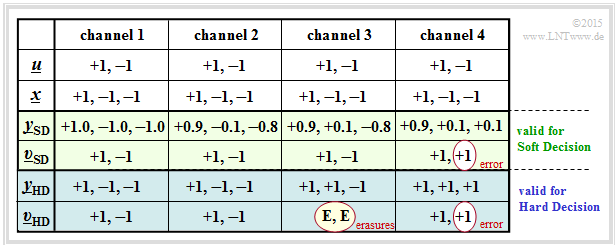
Thus, the four columns in the table differ only by different AWGN realizations.
$\text{Definitions:}$ From the example table you can see:
- $\text{Hard Decision:}$ The sink symbol sequence $\underline{v}_{\rm HD}$ results from the "hard decided channel values" $\underline{y}_{\rm HD}$ $($blue background$)$.
In our example, only the constellations according to $\text{channel 1}$ and $\text{channel 2}$ are decoded without errors.
- $\text{Soft Decision:}$ The sink symbol sequence $\underline{v}_{\rm SD}$ results from the "soft channel output values" $\underline{y}_{\rm SD}$ $($green background$)$.
Now, in this example, it is also correctly decided at $\text{channel 3}$.
The entries in the example table above are to be interpreted as follows:
- For ideal channel ⇒ $\text{channel 1}$ ⇒ $\underline{x} = \underline{y}_{\rm SD} = \underline{y}_{\rm HD}$ there is no difference between the (blue) conventional hard decision variant $\rm {(ML–HD)}$ and the (green) soft decision variant $\rm {(ML–SD)}$.
- The setting according to $\text{channel 2}$ demonstrates low signal distortions. Because of $\underline{y}_{\rm HD} = \underline{x}$ $($which means that the channel does not distort the signs$)$ also $\rm ML–HD$ gives the correct result $\underline{v}_{\rm HD} = \underline{u}$.
- At $\text{channel 3}$ there is $\underline{y}_{\rm HD} ≠ \underline{x}$ and there is also no ${\rm SPC} \ (3, 2)$ assignment $\underline{u}$ ⇒ $\underline{y}_{\rm HD}$. The maximum Likelihood decoder reports here by outputting $\underline{v}_{\rm HD} = \rm (E, \ E)$ that it failed in decoding this block. "$\rm E$" stands for an $\text{Erasure}$ .
- Also the soft decision decoder recognizes that decoding based on the signs does not work. Based on the $\underline{y}_{\rm SD}$ values, however, it recognizes that with high probability the second bit has been falsified and decides to use the correct symbol sequence $\underline{v}_{\rm SD} = (+1, \, -1) = \underline{u}$.
- In $\text{channel 4}$, both the signs of bit 2 and bit 3 are changed by the AWGN channel, leading to the result $\underline{v}_{\rm HD} = (+1, +1) ≠ \underline{u}(+1, \, -1)$ ⇒ a block error and a bit error at the same time. Also the soft decision decoder gives the same wrong result here.
The decoding variant $\rm ML–SD$ also offers the advantage over $\rm ML–HD$ that it is relatively easy to assign a reliability value to each decoding result $($but in the above table this is not specified$)$. This reliability value would
- have its maximum value for $\text{channel 1}$ ,
- be significantly smaller for $\text{channel 2}$ ,
- be close to zero for $\text{channel 3}$ and $\text{channel 4}$.
Reliability information - Log likelihood ratio
Let be $x ∈ \{+1, \, -1\}$ a binary random variable with probabilities ${\rm Pr}(x = +1)$ and ${\rm Pr}(x = \, -1)$. For coding theory, it proves convenient in terms of computation times to use the natural logarithm of the quotient instead of the probabilities ${\rm Pr}(x = ±1)$ .
$\text{Definition:}$ The log likelihood ratio $\rm (LLR)$ of the random variable $x ∈ \{+1, \, -1\}$ is:
- \[L(x)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(x = +1)}{ {\rm Pr}(x = -1)}\hspace{0.05cm}.\]
- For unipolar representation $(+1 → 0$ and $-1 → 1)$ applies accordingly with $\xi ∈ \{0, \, 1\}$:
- \[L(\xi)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(\xi = 0)}{ {\rm Pr}(\xi = 1)}\hspace{0.05cm}.\]
The table gives the nonlinear relationship between ${\rm Pr}(x = ±1)$ and $L(x)$. Replacing ${\rm Pr}(x = +1)$ with ${\rm Pr}(\xi = 0)$, the middle row gives the $L$–value of the unipolar random variable $\xi$.
You can see:
- The more likely random value of $x ∈ \{+1, \, -1\}$ is given by the sign ⇒ ${\rm sign} \ L(x)$.
- In contrast, the absolute value ⇒ $|L(x)|$ indicates the reliability for the result "${\rm sign}(L(x))$".
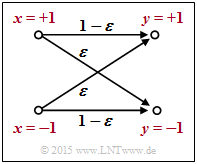
$\text{Example 1:}$ We consider the outlined $\text{BSC model}$ with bipolar representation.
- With the falsification probability $\varepsilon = 0.1$ and the two random variables $x ∈ \{+1, \, -1\}$ and $y ∈ \{+1, \, -1\}$ at the input and output of the channel:
- \[L(y\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(y\hspace{0.05cm}\vert\hspace{0.05cm}x = +1) }{ {\rm Pr}(y\hspace{0.05cm}\vert\hspace{0.05cm}x = -1)} = \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} \big[(1 - \varepsilon)/\varepsilon \big]\\ {\rm ln} \hspace{0.15cm}\big [\varepsilon/(1 - \varepsilon)\big] \end{array} \right.\quad \begin{array}{*{1}c} {\rm for} \hspace{0.15cm} y = +1, \\ {\rm for} \hspace{0.15cm} y = -1. \\ \end{array}\]
- For example, $\varepsilon = 0.1$ results in the following numerical values $($compare the upper table$)$:
- \[L(y = +1\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{0.9}{0.1} = +2.197\hspace{0.05cm}, \hspace{0.8cm} L(y = -1\hspace{0.05cm}\vert\hspace{0.05cm}x) = -2.197\hspace{0.05cm}.\]
- This example shows that the so-called »$\text{LLR algebra}$« can also be applied to conditional probabilities. In "Exercise 4.1Z", the BEC–model is described in a similar way.
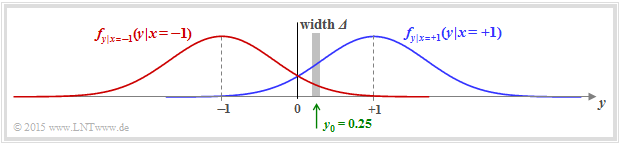
$\text{Example 2:}$ In another example, we consider the $\rm AWGN$ channel with the conditional probability density functions
- \[f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y-1)^2}/(2\sigma^2) } \hspace{0.05cm},\]
- \[f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=-1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y+1)^2}/(2\sigma^2) } \hspace{0.05cm}.\]
⇒ In the graph, two exemplary Gaussian functions are shown as blue and red curves, respectively.
- The total probability density function $\rm (PDF)$ of the output signal $y$ is obtained from the (equally) weighted sum:
- \[f_{y } \hspace{0.05cm} (y ) = 1/2 \cdot \big [ f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 ) \hspace{0.1cm} + \hspace{0.1cm} f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert \hspace{0.05cm}x=-1 ) \big ] \hspace{0.05cm}.\]
- We now calculate the probability that the received value $y$ lies in a (very) narrow interval of width $\it \Delta$ around $y_0 = 0.25$. One obtains approximately
- \[{\rm Pr} (\vert y - y_0\vert \le{\it \Delta}/2 \hspace{0.05cm} \Big \vert \hspace{0.05cm}x=+1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2) } \hspace{0.05cm},\]
- \[{\rm Pr} (\vert y - y_0\vert \le {\it \Delta}/2 \hspace{0.05cm} \Big \vert \hspace{0.05cm}x=-1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2) } \hspace{0.05cm}.\]
- The slightly larger vertical lines denote the conditions, the smaller ones the absolute value.
- The log likelihood ratio $\rm (LLR)$ of the conditional probability in the forward direction $($meaning: output $y$ for a given input $x)$ is thus obtained as the logarithm of the quotient of both expressions:
- \[L(y = y_0\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \left [ \frac{{\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2)}}{{\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2)}} \right ] = {\rm ln} \left [ {\rm e} ^{ - [ {(y_0-1)^2}+{(y_0+1)^2}]/(2\sigma^2)} \right ] = \frac{(y_0+1)^2-(y_0-1)^2}{2\cdot \sigma^2} = \frac{2 \cdot y_0}{\sigma^2}\hspace{0.05cm}. \]
- If we now replace the auxiliary $y_0$ with the general random $y$ at the AWGN output, the final result is:
- \[L(y \hspace{0.05cm}\vert\hspace{0.05cm}x) = {2 \cdot y}/{\sigma^2} =K_{\rm L} \cdot y\hspace{0.05cm}. \]
- Here $K_{\rm L} = 2/\sigma^2$ is a constant that depends solely on the standard deviation of the Gaussian noise component.
Bit-wise soft-in soft-out decoding
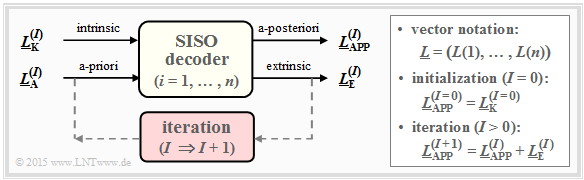
We now assume an $(n, \ k)$ block code where the code word $\underline{x} = (x_1, \ \text{...} \ , \ x_n)$ is falsified by the channel into the received word $\underline{y} = (y_1, \ \text{...} \ , \ y_n)$.
- For long codes, a "maximum-a-posteriori block-level decision" $($for short: $\text{ block-wise MAP}$ – very elaborate.
- One would have to find among the $2^k $ allowable code words $\underline{x}_j ∈ \mathcal{C}$ the one with the greatest a-posteriori probability $\rm (APP)$.
- The code word to output $\underline{z}$ in this case would be
- $$\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}j} \hspace{0.03cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}j} |\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.$$
A second possibility is decoding on bit level. The represented bit-wise $\text{soft-in soft out decoder}$ has the task to decode all code word bits $x_i ∈ \{0, \, 1\}$ according to maximum a-posteriori probability ${\rm Pr}(x_i | \underline{y})$. With the control variable $i = 1, \text{...} , \ n$ holds in this case:
- The corresponding log likelihood ratio for the $i$th code bit is:
- \[L_{\rm APP} (i) = L(x_i\hspace{0.05cm}|\hspace{0.05cm}\underline{y}) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x_i = 0\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}{{\rm Pr}(x_i = 1\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}\hspace{0.05cm} . \]
- The decoder works iteratively. At initialization $($indicated in the diagram by the parameter $I = 0)$ is $L_{\rm APP}(i) = L_{\rm K}(i)$, where the channel $($German: "Kanal" ⇒ "K"$)$ log likelihood ratio $L_{\rm K}(i)$ is given by the received value $y_i$.
- In addition, the extrinsic log likelihood ratio $L_{\rm E}(i)$ is calculated, which quantifies the total information provided by all other bits $(j ≠ i)$ due to the code properties about the considered $i$th bit.
- At the next iteration $(I = 1)$ $L_{\rm E}(i)$ is taken into account in the computation of $L_{\rm APP}(i)$ as a-priori information $L_{\rm A}(i)$. Thus, for the new a-posteriori log likelihood ratio in iteration $I + 1$ holds:
- \[L_{\hspace{0.1cm}\rm APP}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm A}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm E}^{(I)} (i)\hspace{0.05cm} . \]
- The iterations continue until all absolute values $|L_{\rm APP}(i)|$ are greater than a given value. The most likely code word $\underline{z}$ is then obtained from the signs of all $L_{\rm APP}(i)$, with $i = 1, \ \text{...} , \ n$.
- For a $\text{systematic code}$ the first $k$ bits of $\underline{z}$ indicate the information word $\underline{\upsilon}$ being searched for, which will most likely match the message $\underline{u}$ being sent.
This SISO decoder descriptione from [Bos99][1] is intended at this point primarily to clarify the different $L$–values. One recognizes the large potential of the bit-wise decoding only in connection with $\text{concatenated coding systems}$.
Calculation of extrinsic log likelihood ratios
The difficulty in bit-wise $($or symbol-wise$)$ iterative decoding is generally the provision of the extrinsic log likelihood ratios $L_{\rm E}(i)$. For a code of length $n$, the control variable is $i = 1, \ \text{...} , \ n$.
$\text{Definition:}$ The extrinsic log likelihood ratio is a measure of the information that the other symbols $(j ≠ i)$ of the code word provide about the $i$–th encoded symbol, expressed as a log likelihood ratio. We denote this characteristic value by $L_{\rm E}(i)$.
We now calculate the extrinsic log likelihood ratios $L_{\rm E}(i)$ for two example codes.
$\text{(A) Repetition Code}$ ⇒ ${\rm RC} \ (n, 1, n)$
A repetition code $\rm (RC)$ is characterized by the fact that all $n$ encoded symbols $x_i ∈ \{0, \, 1\}$ are identical.
- Here, the extrinsic log likelihood ratio for the $i$–th symbol is very easy to specify:
- \[L_{\rm E}(i) = \hspace{0.05cm}\sum_{j \ne i} \hspace{0.1cm} L_j \hspace{0.3cm}{\rm with}\hspace{0.3cm}L_j = L_{\rm APP}(j) \hspace{0.05cm}.\]
- If the sum over all $L_{j ≠ i}$ is positive ⇒ this implies from the point of view of the other log likelihood ratio values a preference for the decision $x_i = 0$.
- On the other hand, if the sum is negative ⇒ $x_i = 1$ is more likely.
- $L_{\rm E}(i) = 0$ does not allow a prediction.
$\text{Example 5:}$ We consider the decoding of the repetition code $\text{RC (4, 1,4)}$. Thereby, we make three different assumptions for the log likelihood ratio $ \underline{L}_{\rm APP}^{(I=0)}=\underline{L}_{\rm K}.$
$\text{Decoding example (5a):}$
- $$\underline{L}_{\rm APP}^{(I=0)} = (+1, -1, +3, -1)\text{:}$$
- $$L_{\rm E}(1) = -1+3-1 = +1\hspace{0.05cm},$$
- $$L_{\rm E}(2) = +1+3-1 = +3\hspace{0.05cm},$$
- $$L_{\rm E}(3) = +1-1 -1= -1\hspace{0.05cm},$$
- $$L_{\rm E}(4) = +1-1 +3 = +3\hspace{0.05cm}$$
- $$\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm E}^{(I=0)}= (+1, +3, -1, +3) \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm APP}^{(I=1)}=\underline{L}_{\rm APP}^{(I=0)}+ \underline{L}_{\rm E}^{(I=0)}= (+2, +2, +2, +2)$$
- At the beginning $(I=0)$ the positive $L_{\rm E}$ values indicate $x_1 = x_2 = x_4 = 0$ while $x_3 =1$ is more likely $($because of negative $L_{\rm E})$ .
- Already after one iteration $(I=1)$ all $L_{\rm APP}$ values are positive ⇒ the information bit is decoded as $u = 0$.
- Further iterations yield nothing.
$\text{Decoding example (5b):}$
- $$\underline{L}_{\rm APP}^{(I=0)} = (+1, +1, -4, +1)\text{:}$$
- $$\underline{L}_{\rm E}^{(I=0)} = \ (-2, -2, +3, -2)$$
- Although three signs were wrong at the beginning, after two iterations all $L_{\rm APP}$ values are negative.
- The information bit is decoded as $u = 1$.
$\text{Decoding example (5c):}$
- $$\underline{L}_{\rm APP}^{(I=0)} = (+1, +1, -3, +1)\text{:}$$
- $$\underline{L}_{\rm E}^{(I=0)} = (-1, -1, +3, -1)$$
- All $L_{\rm APP}$ values are zero already after one iteration.
- The information bit cannot be decoded, although the initial situation was not much worse than with $\rm (5b)$.
- Further iterations bring nothing here.
$\text{(B) Single parity–check code}$ ⇒ ${\rm SPC} \ (n, \ n \, -1, \ 2)$
For each single parity–check code, the number of "ones" in each code word is even. Or, put another way: For each code word $\underline{x}$ the $\text{Hamming weight}$ $w_{\rm H}(\underline{x})$ is even.
$\text{Definition:}$ Let the code word $\underline{x}^{(–i)}$ contain all symbols except $x_i$ ⇒ vector of length $n–1$. Thus, the "extrinsic log likelihood ratio" will be with respect to the $i$–th symbol, when $\underline{x}$ has been received:
- \[L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} \vert\hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} \vert \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.\]
- As will be shown in the "Exercise 4.4", it is also possible to write for this:
- \[L_{\rm E}(i) = 2 \cdot {\rm tanh}^{-1} \hspace{0.1cm} \left [ \prod\limits_{j \ne i}^{n} \hspace{0.15cm}{\rm tanh}(L_j/2) \right ] \hspace{0.3cm}{\rm with}\hspace{0.3cm}L_j = L_{\rm APP}(j) \hspace{0.05cm}.\]
$\text{Example 6:}$ We assume a "Single parity–check code" with $n = 3, \ k = 2$ ⇒ briefly ${\rm SPC} \ (3, \ 2, \ 2)$.
- The $2^k = 4$ valid code words $\underline{x} = \{x_1,\ x_2,\ x_3\}$ are for bipolar description ⇒ $x_i ∈ \{±1\}$:
- $$ \underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{-0.05cm}, $$
- $$\underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, $$
- $$\underline{x}_2 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} +1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, $$
- $$\underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} +1)\hspace{-0.05cm}. $$
- So, the product $x_1 \cdot x_2 \cdot x_3$ is always positive.
- The table shows the decoding process for $\underline{L}_{\rm APP} = (+2.0, +0.4, \, –1.6)$.
- The hard decision according to the signs of $L_{\rm APP}(i)$ would yield here $(+1, +1, \, -1)$ ⇒ no valid code word of ${\rm SP}(3, \ 2, \ 2)$.
- On the right side of the table, the corresponding extrinsic log likelihood ratios are entered:
- \[L_{\rm E}(1) = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (0.2) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.131\hspace{0.05cm}, \]
- \[L_{\rm E}(2) =2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.518\hspace{0.05cm}, \]
- \[L_{\rm E}(3) =2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (0.2)\hspace{0.05cm}\right ] = +0.151\hspace{0.05cm}.\]
The second equation can be interpreted as follows:
- $L_{\rm APP}(1) = +2.0$ and $L_{\rm APP}(3) = \, -1.6$ state that the first bit is more likely to be "$+1$" than "$-1$" and the third bit is more likely to be "$-1"$ than "$+1$".
- The reliability $($the amount$)$ is slightly greater for the first bit than for the third.
- The extrinsic information $L_{\rm E}(2) = \, -0.518$ considers only the information of bit 1 and bit 3 about bit 2.
- From their point of view, the second bit is "$-1$" with reliability $0.518$.
- The log likelihood ratio $L_{\rm APP}^{I=0}(2) = +0.4$ derived from the received value $y_2$ has suggested "$+1$" for the second bit.
- But the discrepancy is resolved here already in the iteration $I = 1$. The decision falls here for the code word $\underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm},$.
- For $0.518 < L_{\rm APP}(2) < 1.6$ the result $\underline{x}_1$ would only be available after several iterations. For $L_{\rm APP}(2) > 1.6$ on the other hand, the decoder returns $\underline{x}_0$.
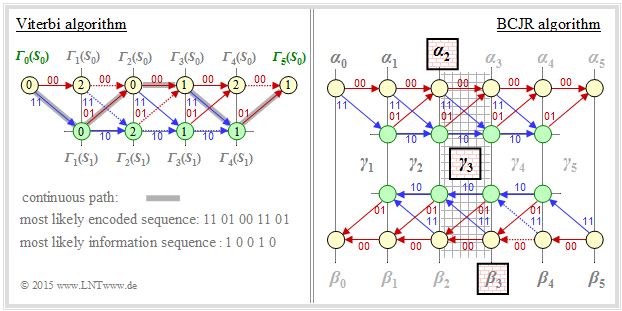
BCJR decoding: Forward-backward algorithm
An example of iterative decoding of convolutional codes is the »BCJR algorithm«, named after its inventors L. R. Bahl, J. Cocke, F. Jelinek, and J. Raviv ⇒ [BCJR74][2]. The algorithm has many parallels to the seven-year older Viterbi decoding, but also some significant differences:
- While Viterbi estimates the total sequence ⇒ $\text{block–wise maximum likelihood}$, the BCJR– Algorithm minimizes the bit error probability ⇒ $\text{bit–wise MAP}$.
- The Viterbi algorithm $($in its original form$)$ cannot process soft information. In contrast, the BCJR algorithm specifies a reliability value for each individual bit at each iteration, which is taken into account in subsequent iterations.
The figure is intended to illustrate $($in an almost inadmissibly simplified way$)$ the different approach of Viterbi and BCJR algorithm. This is based on a convolutional code with memory $m = 1$ and length $L = 4$ ⇒ total length $($with termination$)$ $L' = 5$.
- Viterbi searches and finds the most likely path from ${\it \Gamma}_0(S_0)$ to ${\it \Gamma}_5(S_0)$, namely $S_0 → S_1 → S_0 → S_0 → S_1→ S_0 $. We refer to the sample solution to "Exercise 3.9Z".
- The sketch for the BCJR algorithm illustrates the extraction of the extrinsic L–value for the third symbol ⇒ $L_{\rm E}(3)$. The relevant area in the trellis is shaded:
- Working through the trellis diagram in the forward direction, one obtains in the same way as Viterbi the metrics $\alpha_1, \ \alpha_2, \ \text{...}\hspace{0.05cm} , \ \alpha_5$. To calculate $L_{\rm E}(3)$ one needs from this $\alpha_2$.
- Then we traverse the trellis diagram backwards $($i.e. from right to left$)$ and thus obtain the metrics $\beta_4, \ \beta_3, \ \text{...}\hspace{0.05cm} , \ \beta_0$ corresponding to the sketch below.
- The extrinsic log likelihood ratio $L_{\rm E}(3)$ is obtained from the forward direction metric $\alpha_2$ and the backward direction metric $\beta_3$ and the a-priori information $\gamma_3$ about the symbol $i = 3$.
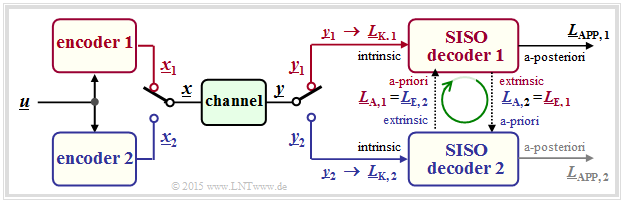
Basic structure of concatenated coding systems
The most important communication systems of the last years use two different channel codes. One speaks then of »concatenated codes«. Even with relatively short component codes $\mathcal{C}_1$ and $\mathcal{C}_2$ the concatenated code $\mathcal{C}$ results in a sufficiently large code word length $n$, which is known to be necessary to approach the channel capacity.
To begin with, here are a few examples from mobile communications:
- In $\rm GSM$ $($"Global System for Mobile Communications", the second generation of mobile communication systems$)$, the data bit rate is first increased from $9. 6 \ \rm kbit/s$ to $12 \ \rm kbit/s$ in order to enable error detection in circuit-switched networks as well. This is followed by a punctured convolutional code with the output bit rate $22.8 \ \rm kbit/s$. The total code rate is thus about $0.421$.
- In the 3G cellular system $\rm UMTS$ $($"Universal Mobile Telecommunications System"), depending on the boundary conditions $($good/bad channel, few/many subscribers in the cell$)$ one uses a $\text{convolutional code}$ or a $\text{turbo code}$ $($by this one understands per se the concatenation of two convolutional encoders$)$.
- In 4G mobile communication systems $\rm LTE$ $($"Long Term Evolution"$)$, a convolutional code is used for short control signals, turbo code for the longer payload data.
The graph shows the basic structure of a parallel concatenated coding system. All vectors consist of $n$ elements:
- $$\underline{L} = (L(1), \ \text{...}\hspace{0.05cm} , \ L(n)).$$
So the calculation of all L–values is done on symbol level. Not shown here is the $\rm interleaver$, which is mandatory e.g. for turbo codes.
- The sequences $\underline{x}_1$ and $\underline{x}_2$ are combined to form the vector $\underline{x}$ for joint transmission over the channel by a multiplexer.
- At the receiver, the sequence $\underline{y}$ is again decomposed into the parts $\underline{y}_1$ and $\underline{y}_2$. From this the channel L–values $\underline{L}_{\rm K,\hspace{0.05cm}1} $ and $\underline{L}_{\rm K,\hspace{0.05cm}2}$ are formed.
- The symbol-wise decoder determines the extrinsic log likelihood ratios $\underline{L}_{\rm E,\hspace{0.05cm} 1}$ and $\underline{L}_{\rm E,\hspace{0.05cm} 2}$, which are also the a-priori information $\underline{L}_{\rm A,\hspace{0.05cm} 2}$ and $\underline{L}_{\rm A,\hspace{0.05cm} 1}$ for the other decoder.
- After a sufficient number of iterations $($i.e. when a termination criterion is met$)$, the vector $\underline{L}_{\rm APP}$ of a-posteriori values is available at the decoder output.
- In the example, the value in the upper branch is taken arbitrarily.
- However, the lower log likelihood ratio would also be possible.
The above model also applies in particular to the decoding of turbo codes according to the chapter "Basic structure of a turbo code".
Exercises for the chapter
Exercise 4.1: Log Likelihood Ratio
Exercise 4.1Z: Log Likelihood Ratio at the BEC Model
Exercise 4.2: Channel Log Likelihood Ratio at AWGN
Exercise 4.3: Iterative Decoding at the BSC
Exercise 4.3Z: Conversions of L-value and S-value
Exercise 4.4: Extrinsic L-values at SPC
Exercise 4.4Z: Supplement to Exercise 4.4
Exercise 4.5: On the Extrinsic L-values again
Exercise 4.5Z: Tangent Hyperbolic and Inverse
References