Difference between revisions of "Aufgaben:Exercise 2.7: Is the Modulation Depth Too High?"
m |
m |
||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Envelope_Demodulation |
}} | }} | ||
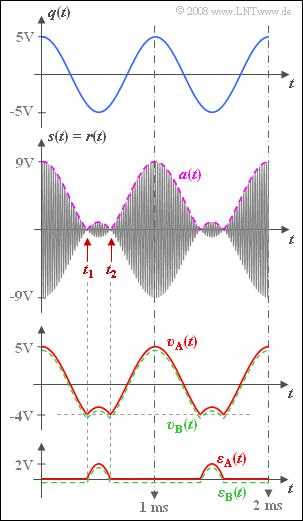
| − | [[File:P_ID1032__Mod_A_2_7.png|right|frame|Signal waveforms for "DSB–AM with carrier"]] | + | [[File:P_ID1032__Mod_A_2_7.png|right|frame|Signal waveforms for "DSB–AM with carrier"]] |
| − | The cosine-shaped source signal $q(t)$ with amplitude $A_{\rm N} = 5\ \rm V$ and frequency $f_{\rm N} = 1 \ \rm kHz$ is $\rm | + | The cosine-shaped source signal $q(t)$ with amplitude $A_{\rm N} = 5\ \rm V$ and frequency $f_{\rm N} = 1 \ \rm kHz$ is $\rm DSB$ amplitude modulated. Assuming an ideal channel, the received signal is given by: |
:$$r(t) = s(t) =\left(q(t) + A_{\rm T}\right) \cdot \cos (2\pi \cdot f_{\rm T}\cdot t )\hspace{0.05cm}.$$ | :$$r(t) = s(t) =\left(q(t) + A_{\rm T}\right) \cdot \cos (2\pi \cdot f_{\rm T}\cdot t )\hspace{0.05cm}.$$ | ||
| − | Thus, we are dealing with "DSB–AM with carrier”. | + | Thus, we are dealing with "DSB–AM with carrier”. |
| − | In the graph, besides the source signal $q(t)$ | + | In the graph, besides the source signal $q(t)$, and the received signal $r(t)$ including its envelope $a(t)$, we can also see the sink signal $v(t)$ and the error signal |
:$$ \varepsilon(t) = v(t) - q(t).$$ | :$$ \varepsilon(t) = v(t) - q(t).$$ | ||
The sink signal drawn in red, | The sink signal drawn in red, | ||
:$$v_{\rm A}(t) = a(t) - A_{\rm T}$$ | :$$v_{\rm A}(t) = a(t) - A_{\rm T}$$ | ||
| − | belongs to an envelope demodulator, where exactly the carrier added at the transmitter $(A_{\rm T})$ is subtracted from the envelope $a(t)$ | + | belongs to an envelope demodulator, where exactly the carrier added at the transmitter $(A_{\rm T})$ is subtracted from the envelope $a(t)$. |
| − | This signal $v_{\rm A}(t)$ contains a DC component just like the corresponding error signal $ε_{\rm A}(t)$ . Due to the periodicity, it can be approximated by the following Fourier | + | This signal $v_{\rm A}(t)$ contains a DC component just like the corresponding error signal $ε_{\rm A}(t)$ . Due to the periodicity, it can be approximated by the following Fourier series: |
:$$v_{\rm A}(t) = A_0 + \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ), \hspace{0.3cm}{\rm with}$$ | :$$v_{\rm A}(t) = A_0 + \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ), \hspace{0.3cm}{\rm with}$$ | ||
| − | :$$A_0 = 0.272\,{\rm V},\hspace{0.3cm}A_1 = 4.480\,{\rm V},\hspace{0.3cm}A_2 = 0.458\,{\rm V},\hspace{0.3cm}A_3 = -0.367\,{\rm V},\hspace{0.3cm}$$ | + | ::$$A_0 = 0.272\,{\rm V},\hspace{0.3cm}A_1 = 4.480\,{\rm V},\hspace{0.3cm}A_2 = 0.458\,{\rm V},\hspace{0.3cm}A_3 = -0.367\,{\rm V},\hspace{0.3cm}$$ |
| − | :$$A_4 = 0.260\,{\rm V},\hspace{0.3cm}A_5 = -0.155\,{\rm V},\hspace{0.3cm}A_6 = 0.066\,{\rm V}\hspace{0.05cm}.$$ | + | ::$$A_4 = 0.260\,{\rm V},\hspace{0.3cm}A_5 = -0.155\,{\rm V},\hspace{0.3cm}A_6 = 0.066\,{\rm V}\hspace{0.05cm}.$$ |
| − | If the DC component is instead removed using an ideal high-pass filter, this would result in the DC-free signals | + | If the DC component is instead removed using an ideal high-pass filter, this would result in the DC-free signals |
| − | :$$ v_{\rm B}(t) = \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ), | + | :$$ v_{\rm B}(t) = \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ),$$ |
| + | :$$ \varepsilon_{\rm B}(t) = v_{\rm B}(t) - q(t) = a(t) - A_{\rm T} - A_0 \hspace{0.05cm}.$$ | ||
| Line 26: | Line 27: | ||
| − | + | Hints: | |
*This exercise belongs to the chapter [[Modulation_Methods/Envelope_Demodulation|Envelope Demodulation]]. | *This exercise belongs to the chapter [[Modulation_Methods/Envelope_Demodulation|Envelope Demodulation]]. | ||
| − | *Particular reference is made to the chapter [[Modulation_Methods/Quality_Criteria|Quality Criteria]] in this book, as well as the chapter [[Linear_and_Time_Invariant_Systems/Nonlinear_Distortions|Nonlinear Distortions]] in the book "Linear and Time Invariant Systems". | + | *Particular reference is made to the chapter [[Modulation_Methods/Quality_Criteria|Quality Criteria]] in this book, as well as the chapter [[Linear_and_Time_Invariant_Systems/Nonlinear_Distortions|Nonlinear Distortions]] in the book "Linear and Time Invariant Systems". |
| − | + | *To solve these problems, the following indefinite integrals are given: | |
| − | *To solve these problems, the following indefinite integrals are given: | ||
:$$ \int { \cos (a x )}\hspace{0.1cm}{\rm d}x =\frac{1}{a} \cdot \sin (a x ), \hspace{0.5cm} \int { \cos^2 (a x )}\hspace{0.1cm}{\rm d}x = \frac{x}{2} +\frac{1}{4a} \cdot \sin (2a x ).$$ | :$$ \int { \cos (a x )}\hspace{0.1cm}{\rm d}x =\frac{1}{a} \cdot \sin (a x ), \hspace{0.5cm} \int { \cos^2 (a x )}\hspace{0.1cm}{\rm d}x = \frac{x}{2} +\frac{1}{4a} \cdot \sin (2a x ).$$ | ||
*The distortion factors are calculated according to the formulas: | *The distortion factors are calculated according to the formulas: | ||
| Line 46: | Line 46: | ||
$m \ = \ $ { 1.25 3% } | $m \ = \ $ { 1.25 3% } | ||
| − | { | + | {At which times $t_1$ and $t_2$ (see graph) does the envelope first $a(t)$ become zero? |
|type="{}"} | |type="{}"} | ||
$t_1 \ = \ $ { 0.4 3% } $\ \rm ms$ | $t_1 \ = \ $ { 0.4 3% } $\ \rm ms$ | ||
$t_2 \ = \ $ { 0.6 3% } $\ \rm ms$ | $t_2 \ = \ $ { 0.6 3% } $\ \rm ms$ | ||
| − | { | + | {Calculate the distortion factors $K_2$, ... , $K_6$ as well as the total distortion factor $K$. |
|type="{}"} | |type="{}"} | ||
$K \ = \ $ { 14.8 3% } $\text{%}$ | $K \ = \ $ { 14.8 3% } $\text{%}$ | ||
| − | { | + | {Calculate the power $P_{ε{\rm A}} = Ε\big [ε_{\rm A}^2(t)\big ]$ for the red error signal $ε_{\rm A}(t)$. |
|type="{}"} | |type="{}"} | ||
$P_{ε{\rm A}} \ = \ $ { 0.432 3% } $\ \rm V^2$ | $P_{ε{\rm A}} \ = \ $ { 0.432 3% } $\ \rm V^2$ | ||
| − | { | + | {Calculate the power $P_{ε{\rm B}} = Ε\big [ε_{\rm B}^2(t)\big ]$ for the green error signal $ε_{\rm B}(t)$. |
|type="{}"} | |type="{}"} | ||
$P_{ε{\rm B}} \ = \ $ { 0.358 3% } $\ \rm V^2$ | $P_{ε{\rm B}} \ = \ $ { 0.358 3% } $\ \rm V^2$ | ||
| − | { | + | {Calculate the corresponding sink SNR $ρ_v = P_q/P_ε$ for both demodulators. |
|type="{}"} | |type="{}"} | ||
$ρ_{v{\rm A}} \ = \ $ { 28.94 3% } | $ρ_{v{\rm A}} \ = \ $ { 28.94 3% } | ||
| Line 69: | Line 69: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' From the graph we can see that $A_{\rm T} = 4\ \rm V$. With $A_{\rm N} = 5\ \rm V$ this results in the modulation depth |
:$$m = A_{\rm N}/A_{\rm T}\hspace{0.15cm}\underline { = 1.25}.$$ | :$$m = A_{\rm N}/A_{\rm T}\hspace{0.15cm}\underline { = 1.25}.$$ | ||
| − | '''(2)''' | + | '''(2)''' From the condition $a(t) = q(t) + A_{\rm T} = 0$ it follows directly for the first zero crossing: |
:$$ \cos (2\pi \cdot f_{\rm N}\cdot t_1 ) = \frac{-A_{\rm T}}{A_{\rm N}}= -0.8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}t_1 = \frac{\rm arccos(-0.8)}{2\pi \cdot f_{\rm N}}\approx \frac{0.795 \cdot \pi}{2\pi \cdot f_{\rm N}} \hspace{0.05cm}.$$ | :$$ \cos (2\pi \cdot f_{\rm N}\cdot t_1 ) = \frac{-A_{\rm T}}{A_{\rm N}}= -0.8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}t_1 = \frac{\rm arccos(-0.8)}{2\pi \cdot f_{\rm N}}\approx \frac{0.795 \cdot \pi}{2\pi \cdot f_{\rm N}} \hspace{0.05cm}.$$ | ||
| − | * | + | *When $f_{\rm N} = 1 \ \rm kHz$ this gives $t_1\hspace{0.15cm}\underline { ≈ 0.4 \ \rm ms}$. |
| − | * | + | *Accordingly, the second zero crossing is at $t_2\hspace{0.15cm}\underline { ≈ 0.6 \ \rm ms}$. |
| − | '''(3)''' | + | '''(3)''' The second order distortion factor is $K_2 = 0.458/4.48 ≈ 0.102$. |
| − | * | + | *Correspondingly, the third order distortion factor is: $K_3 = 0.367/4.48 ≈ 0.082$. |
| − | * | + | *The further distortion factors are $K_4 ≈ 0.058$, $K_5 ≈ 0.035$ and $K_6 ≈ 0.015$. |
| − | * | + | *Thus, for the total distortion factor we get: |
:$$ K = \sqrt{K_2^2 + K_3^2 + K_4^2 + K_5^2 + K_6^2 }\hspace{0.15cm}\underline { \approx 14.8 \%}.$$ | :$$ K = \sqrt{K_2^2 + K_3^2 + K_4^2 + K_5^2 + K_6^2 }\hspace{0.15cm}\underline { \approx 14.8 \%}.$$ | ||
| − | '''(4)''' | + | '''(4)''' The distortion power is obtained by averaging $ε_{\rm A}(t)^2$ over the period $T_0 = 1\ \rm ms$: |
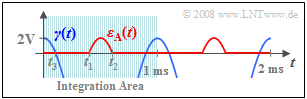
| − | [[File:EN_Mod_A_2_7_d.png|right|frame| | + | [[File:EN_Mod_A_2_7_d.png|right|frame|Calculating the distortion power]] |
:$$P_{\varepsilon \rm A} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{t_1}^{\hspace{0.1cm} t_2} {\varepsilon_{\rm A}^2(t) }\hspace{0.1cm}{\rm d}t = \frac{I_{\varepsilon}}{T_{\rm 0}}\hspace{0.05cm}.$$ | :$$P_{\varepsilon \rm A} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{t_1}^{\hspace{0.1cm} t_2} {\varepsilon_{\rm A}^2(t) }\hspace{0.1cm}{\rm d}t = \frac{I_{\varepsilon}}{T_{\rm 0}}\hspace{0.05cm}.$$ | ||
| − | * | + | *This takes into account that the error signal $ε_{\rm A}(t)$ is equal to zero outside of the interval from $t_1$ to $t_2$. |
| − | * | + | *As seen from the graph, $I_ε$ is twice as large as the integral $I_γ$ of the auxiliary quantity $γ$ in the interval from zero to $t_3 = (t_2 – t_1)/2 ≈ 0.1 \ \rm ms$: |
| − | :$$I_{\gamma} = \int_{0}^{\hspace{0.1cm} t_3} {\gamma^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.5cm}{\rm | + | :$$I_{\gamma} = \int_{0}^{\hspace{0.1cm} t_3} {\gamma^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.5cm}{\rm with}\hspace{0.5cm} \gamma(t) = 2 \cdot \left( A_{\rm N} \cdot \cos (\omega_{\rm N}\cdot t ) - A_{\rm T}\right)\hspace{0.05cm}.$$ |
| − | * | + | *An additional calculation yields $I_{\gamma} = 4 \cdot \left( I_1 + I_2 + I_3 \right)$ with |
:$$I_1 = A_{\rm N}^2 \cdot \int_{0}^{\hspace{0.1cm} t_3} {\cos^2 (\omega_{\rm N}\cdot t ) }\hspace{0.1cm}{\rm d}t = A_{\rm N}^2 \cdot \left[ \frac{t_3}{2} + \frac{\sin (2 \omega_{\rm N}\cdot t_3 )}{4 \omega_{\rm N}} \right] = 25\,{\rm V}^2 \cdot \left[ 0.05\,{\rm ms} + 0.0378\,{\rm ms} \right] = 2.196 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm},$$ | :$$I_1 = A_{\rm N}^2 \cdot \int_{0}^{\hspace{0.1cm} t_3} {\cos^2 (\omega_{\rm N}\cdot t ) }\hspace{0.1cm}{\rm d}t = A_{\rm N}^2 \cdot \left[ \frac{t_3}{2} + \frac{\sin (2 \omega_{\rm N}\cdot t_3 )}{4 \omega_{\rm N}} \right] = 25\,{\rm V}^2 \cdot \left[ 0.05\,{\rm ms} + 0.0378\,{\rm ms} \right] = 2.196 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm},$$ | ||
:$$ I_2 = - 2 \cdot A_{\rm N}\cdot A_{\rm T} \cdot \int_{0}^{\hspace{0.1cm} t_3} \hspace{-0.2cm}{\cos (\omega_{\rm N}\cdot t ) }\hspace{0.1cm}{\rm d}t = - 2 \cdot A_{\rm N}\cdot A_{\rm T} \cdot \frac{\sin (\omega_{\rm N}\cdot t_3 )}{\omega_{\rm N}} = - 2 \cdot 5\,{\rm V} \cdot 4\,{\rm V}\cdot 0.0935\,{\rm ms} = -3.742 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm},$$ | :$$ I_2 = - 2 \cdot A_{\rm N}\cdot A_{\rm T} \cdot \int_{0}^{\hspace{0.1cm} t_3} \hspace{-0.2cm}{\cos (\omega_{\rm N}\cdot t ) }\hspace{0.1cm}{\rm d}t = - 2 \cdot A_{\rm N}\cdot A_{\rm T} \cdot \frac{\sin (\omega_{\rm N}\cdot t_3 )}{\omega_{\rm N}} = - 2 \cdot 5\,{\rm V} \cdot 4\,{\rm V}\cdot 0.0935\,{\rm ms} = -3.742 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm},$$ | ||
:$$ I_3 = A_{\rm T}^2 \cdot \int_{0}^{\hspace{0.1cm} t_3} {}\hspace{0.1cm}{\rm d}t = A_{\rm T}^2 \cdot {t_3} = 1.6 \cdot 10^{-3}\,{\rm V^2 s}$$ | :$$ I_3 = A_{\rm T}^2 \cdot \int_{0}^{\hspace{0.1cm} t_3} {}\hspace{0.1cm}{\rm d}t = A_{\rm T}^2 \cdot {t_3} = 1.6 \cdot 10^{-3}\,{\rm V^2 s}$$ | ||
:$$\Rightarrow \hspace{0.3cm}I_{\gamma} = 0.216 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}I_{\varepsilon} = 2 \cdot I_{\gamma} =0.432 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm}I_{\gamma} = 0.216 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}I_{\varepsilon} = 2 \cdot I_{\gamma} =0.432 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm}.$$ | ||
| − | * | + | *Thus, the final result is obtained as: |
:$$P_{\varepsilon \rm A} = {I_{\varepsilon}}/{T_{\rm 0}}\hspace{0.15cm}\underline {=0.432 \,{\rm V^2 }}\hspace{0.05cm}.$$ | :$$P_{\varepsilon \rm A} = {I_{\varepsilon}}/{T_{\rm 0}}\hspace{0.15cm}\underline {=0.432 \,{\rm V^2 }}\hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | '''(5)''' The two sink signals $v_{\rm A}(t)$ and $v_{\rm B}(t)$ differ by the DC component $A_0$, as do the two error signals $ε_{\rm A}(t)$ and $ε_{\rm B}(t)$. Therefore: |
:$$ P_{\varepsilon \rm B} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm B}^2(t) }\hspace{0.1cm}{\rm d}t = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\left[\varepsilon_{\rm A}(t) - A_0 \right]^2}\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$ | :$$ P_{\varepsilon \rm B} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm B}^2(t) }\hspace{0.1cm}{\rm d}t = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\left[\varepsilon_{\rm A}(t) - A_0 \right]^2}\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$ | ||
| − | * | + | *This can also be written as: |
:$$P_{1} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm A}^2(t) }\hspace{0.1cm}{\rm d}t = P_{\varepsilon \rm A} \hspace{0.05cm},\hspace{0.3cm} | :$$P_{1} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm A}^2(t) }\hspace{0.1cm}{\rm d}t = P_{\varepsilon \rm A} \hspace{0.05cm},\hspace{0.3cm} | ||
P_{2} = - 2 A_0 \cdot \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm A}(t) }\hspace{0.1cm}{\rm d}t = - 2 A_0^2 \hspace{0.05cm},\hspace{0.3cm} | P_{2} = - 2 A_0 \cdot \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm A}(t) }\hspace{0.1cm}{\rm d}t = - 2 A_0^2 \hspace{0.05cm},\hspace{0.3cm} | ||
P_{3} = A_0^2 \cdot \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} { }\hspace{0.1cm}{\rm d}t = A_0^2 \hspace{0.05cm}.$$ | P_{3} = A_0^2 \cdot \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} { }\hspace{0.1cm}{\rm d}t = A_0^2 \hspace{0.05cm}.$$ | ||
| − | * | + | *This gives the power of the error signal $ε_{\rm B}(t)$: |
:$$P_{\varepsilon \rm B} = P_{\varepsilon \rm A}- A_0^2 = 0.432\,{\rm V}^2 - (0.272\,{\rm V})^2 \hspace{0.15cm}\underline {= 0.358\,{\rm V}^2} \hspace{0.05cm}.$$ | :$$P_{\varepsilon \rm B} = P_{\varepsilon \rm A}- A_0^2 = 0.432\,{\rm V}^2 - (0.272\,{\rm V})^2 \hspace{0.15cm}\underline {= 0.358\,{\rm V}^2} \hspace{0.05cm}.$$ | ||
| − | * | + | *A similar result would have been obtained from the following calculation: |
:$$ P_{\varepsilon \rm B} = \frac{1\,{\rm V}^2}{2} \cdot \left[ (5 - 4.48)^2 + 0.458^2 + 0.367^2 + ... + 0.066^2 \right] \approx 0.356\,{\rm V}^2 \hspace{0.05cm}.$$ | :$$ P_{\varepsilon \rm B} = \frac{1\,{\rm V}^2}{2} \cdot \left[ (5 - 4.48)^2 + 0.458^2 + 0.367^2 + ... + 0.066^2 \right] \approx 0.356\,{\rm V}^2 \hspace{0.05cm}.$$ | ||
| − | * | + | *The small difference in both calculation processes is due to the fact that the Fourier coefficients $A_7$, $A_8$, ..., are very small, but not zero. |
| − | '''(6)''' | + | '''(6)''' The power of the source signal $q(t)$ is $P_q = A_{\rm N}^2/2 = 12.5 V^2$. This gives the two S/N ratios: |
:$$\rho_{v {\rm A}} = \frac{P_{q}}{P_{\varepsilon \rm A}} \hspace{0.15cm}\underline {= 28.94} \hspace{0.05cm}, \hspace{0.3cm} \rho_{v {\rm B}} = \frac{P_{q}}{P_{\varepsilon \rm B}}\hspace{0.15cm}\underline { = 34.92} \hspace{0.05cm}.$$ | :$$\rho_{v {\rm A}} = \frac{P_{q}}{P_{\varepsilon \rm A}} \hspace{0.15cm}\underline {= 28.94} \hspace{0.05cm}, \hspace{0.3cm} \rho_{v {\rm B}} = \frac{P_{q}}{P_{\varepsilon \rm B}}\hspace{0.15cm}\underline { = 34.92} \hspace{0.05cm}.$$ | ||
| − | * | + | *This shows that the envelope demodulator $\rm B$ (using a high-pass) is better than the demodulator $\rm A$ (using subtraction) by about $6 \ \rm dB$. |
| − | + | *It should also be noted that the approximation $ρ_v = α_2 · P_q/K^2$ would here lead to the distorted numerical value $ρ_v = 36.66$. | |
| − | * | + | *This different result is justified in detail on the page "The distortion factor" in the book "Linear and Time Invariant systems", based exactly on the same assumptions made for this exercise. |
| − | * | ||
Latest revision as of 16:24, 31 March 2022
The cosine-shaped source signal $q(t)$ with amplitude $A_{\rm N} = 5\ \rm V$ and frequency $f_{\rm N} = 1 \ \rm kHz$ is $\rm DSB$ amplitude modulated. Assuming an ideal channel, the received signal is given by:
- $$r(t) = s(t) =\left(q(t) + A_{\rm T}\right) \cdot \cos (2\pi \cdot f_{\rm T}\cdot t )\hspace{0.05cm}.$$
Thus, we are dealing with "DSB–AM with carrier”.
In the graph, besides the source signal $q(t)$, and the received signal $r(t)$ including its envelope $a(t)$, we can also see the sink signal $v(t)$ and the error signal
- $$ \varepsilon(t) = v(t) - q(t).$$
The sink signal drawn in red,
- $$v_{\rm A}(t) = a(t) - A_{\rm T}$$
belongs to an envelope demodulator, where exactly the carrier added at the transmitter $(A_{\rm T})$ is subtracted from the envelope $a(t)$.
This signal $v_{\rm A}(t)$ contains a DC component just like the corresponding error signal $ε_{\rm A}(t)$ . Due to the periodicity, it can be approximated by the following Fourier series:
- $$v_{\rm A}(t) = A_0 + \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ), \hspace{0.3cm}{\rm with}$$
- $$A_0 = 0.272\,{\rm V},\hspace{0.3cm}A_1 = 4.480\,{\rm V},\hspace{0.3cm}A_2 = 0.458\,{\rm V},\hspace{0.3cm}A_3 = -0.367\,{\rm V},\hspace{0.3cm}$$
- $$A_4 = 0.260\,{\rm V},\hspace{0.3cm}A_5 = -0.155\,{\rm V},\hspace{0.3cm}A_6 = 0.066\,{\rm V}\hspace{0.05cm}.$$
If the DC component is instead removed using an ideal high-pass filter, this would result in the DC-free signals
- $$ v_{\rm B}(t) = \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ),$$
- $$ \varepsilon_{\rm B}(t) = v_{\rm B}(t) - q(t) = a(t) - A_{\rm T} - A_0 \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter Envelope Demodulation.
- Particular reference is made to the chapter Quality Criteria in this book, as well as the chapter Nonlinear Distortions in the book "Linear and Time Invariant Systems".
- To solve these problems, the following indefinite integrals are given:
- $$ \int { \cos (a x )}\hspace{0.1cm}{\rm d}x =\frac{1}{a} \cdot \sin (a x ), \hspace{0.5cm} \int { \cos^2 (a x )}\hspace{0.1cm}{\rm d}x = \frac{x}{2} +\frac{1}{4a} \cdot \sin (2a x ).$$
- The distortion factors are calculated according to the formulas:
- $$K_2 = {A_2}/{A_1}, \hspace{0.3cm} K_3 = {A_3}/{A_1}, \hspace{0.1cm} \text{...} \hspace{0.5cm} \Rightarrow \hspace{0.5cm}K = \sqrt{K_2^2 +K_3^2 + \text{...}}\hspace{0.1cm} .$$
Questions
Solution
- $$m = A_{\rm N}/A_{\rm T}\hspace{0.15cm}\underline { = 1.25}.$$
(2) From the condition $a(t) = q(t) + A_{\rm T} = 0$ it follows directly for the first zero crossing:
- $$ \cos (2\pi \cdot f_{\rm N}\cdot t_1 ) = \frac{-A_{\rm T}}{A_{\rm N}}= -0.8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}t_1 = \frac{\rm arccos(-0.8)}{2\pi \cdot f_{\rm N}}\approx \frac{0.795 \cdot \pi}{2\pi \cdot f_{\rm N}} \hspace{0.05cm}.$$
- When $f_{\rm N} = 1 \ \rm kHz$ this gives $t_1\hspace{0.15cm}\underline { ≈ 0.4 \ \rm ms}$.
- Accordingly, the second zero crossing is at $t_2\hspace{0.15cm}\underline { ≈ 0.6 \ \rm ms}$.
(3) The second order distortion factor is $K_2 = 0.458/4.48 ≈ 0.102$.
- Correspondingly, the third order distortion factor is: $K_3 = 0.367/4.48 ≈ 0.082$.
- The further distortion factors are $K_4 ≈ 0.058$, $K_5 ≈ 0.035$ and $K_6 ≈ 0.015$.
- Thus, for the total distortion factor we get:
- $$ K = \sqrt{K_2^2 + K_3^2 + K_4^2 + K_5^2 + K_6^2 }\hspace{0.15cm}\underline { \approx 14.8 \%}.$$
(4) The distortion power is obtained by averaging $ε_{\rm A}(t)^2$ over the period $T_0 = 1\ \rm ms$:
- $$P_{\varepsilon \rm A} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{t_1}^{\hspace{0.1cm} t_2} {\varepsilon_{\rm A}^2(t) }\hspace{0.1cm}{\rm d}t = \frac{I_{\varepsilon}}{T_{\rm 0}}\hspace{0.05cm}.$$
- This takes into account that the error signal $ε_{\rm A}(t)$ is equal to zero outside of the interval from $t_1$ to $t_2$.
- As seen from the graph, $I_ε$ is twice as large as the integral $I_γ$ of the auxiliary quantity $γ$ in the interval from zero to $t_3 = (t_2 – t_1)/2 ≈ 0.1 \ \rm ms$:
- $$I_{\gamma} = \int_{0}^{\hspace{0.1cm} t_3} {\gamma^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.5cm}{\rm with}\hspace{0.5cm} \gamma(t) = 2 \cdot \left( A_{\rm N} \cdot \cos (\omega_{\rm N}\cdot t ) - A_{\rm T}\right)\hspace{0.05cm}.$$
- An additional calculation yields $I_{\gamma} = 4 \cdot \left( I_1 + I_2 + I_3 \right)$ with
- $$I_1 = A_{\rm N}^2 \cdot \int_{0}^{\hspace{0.1cm} t_3} {\cos^2 (\omega_{\rm N}\cdot t ) }\hspace{0.1cm}{\rm d}t = A_{\rm N}^2 \cdot \left[ \frac{t_3}{2} + \frac{\sin (2 \omega_{\rm N}\cdot t_3 )}{4 \omega_{\rm N}} \right] = 25\,{\rm V}^2 \cdot \left[ 0.05\,{\rm ms} + 0.0378\,{\rm ms} \right] = 2.196 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm},$$
- $$ I_2 = - 2 \cdot A_{\rm N}\cdot A_{\rm T} \cdot \int_{0}^{\hspace{0.1cm} t_3} \hspace{-0.2cm}{\cos (\omega_{\rm N}\cdot t ) }\hspace{0.1cm}{\rm d}t = - 2 \cdot A_{\rm N}\cdot A_{\rm T} \cdot \frac{\sin (\omega_{\rm N}\cdot t_3 )}{\omega_{\rm N}} = - 2 \cdot 5\,{\rm V} \cdot 4\,{\rm V}\cdot 0.0935\,{\rm ms} = -3.742 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm},$$
- $$ I_3 = A_{\rm T}^2 \cdot \int_{0}^{\hspace{0.1cm} t_3} {}\hspace{0.1cm}{\rm d}t = A_{\rm T}^2 \cdot {t_3} = 1.6 \cdot 10^{-3}\,{\rm V^2 s}$$
- $$\Rightarrow \hspace{0.3cm}I_{\gamma} = 0.216 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}I_{\varepsilon} = 2 \cdot I_{\gamma} =0.432 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm}.$$
- Thus, the final result is obtained as:
- $$P_{\varepsilon \rm A} = {I_{\varepsilon}}/{T_{\rm 0}}\hspace{0.15cm}\underline {=0.432 \,{\rm V^2 }}\hspace{0.05cm}.$$
(5) The two sink signals $v_{\rm A}(t)$ and $v_{\rm B}(t)$ differ by the DC component $A_0$, as do the two error signals $ε_{\rm A}(t)$ and $ε_{\rm B}(t)$. Therefore:
- $$ P_{\varepsilon \rm B} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm B}^2(t) }\hspace{0.1cm}{\rm d}t = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\left[\varepsilon_{\rm A}(t) - A_0 \right]^2}\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- This can also be written as:
- $$P_{1} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm A}^2(t) }\hspace{0.1cm}{\rm d}t = P_{\varepsilon \rm A} \hspace{0.05cm},\hspace{0.3cm} P_{2} = - 2 A_0 \cdot \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm A}(t) }\hspace{0.1cm}{\rm d}t = - 2 A_0^2 \hspace{0.05cm},\hspace{0.3cm} P_{3} = A_0^2 \cdot \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} { }\hspace{0.1cm}{\rm d}t = A_0^2 \hspace{0.05cm}.$$
- This gives the power of the error signal $ε_{\rm B}(t)$:
- $$P_{\varepsilon \rm B} = P_{\varepsilon \rm A}- A_0^2 = 0.432\,{\rm V}^2 - (0.272\,{\rm V})^2 \hspace{0.15cm}\underline {= 0.358\,{\rm V}^2} \hspace{0.05cm}.$$
- A similar result would have been obtained from the following calculation:
- $$ P_{\varepsilon \rm B} = \frac{1\,{\rm V}^2}{2} \cdot \left[ (5 - 4.48)^2 + 0.458^2 + 0.367^2 + ... + 0.066^2 \right] \approx 0.356\,{\rm V}^2 \hspace{0.05cm}.$$
- The small difference in both calculation processes is due to the fact that the Fourier coefficients $A_7$, $A_8$, ..., are very small, but not zero.
(6) The power of the source signal $q(t)$ is $P_q = A_{\rm N}^2/2 = 12.5 V^2$. This gives the two S/N ratios:
- $$\rho_{v {\rm A}} = \frac{P_{q}}{P_{\varepsilon \rm A}} \hspace{0.15cm}\underline {= 28.94} \hspace{0.05cm}, \hspace{0.3cm} \rho_{v {\rm B}} = \frac{P_{q}}{P_{\varepsilon \rm B}}\hspace{0.15cm}\underline { = 34.92} \hspace{0.05cm}.$$
- This shows that the envelope demodulator $\rm B$ (using a high-pass) is better than the demodulator $\rm A$ (using subtraction) by about $6 \ \rm dB$.
- It should also be noted that the approximation $ρ_v = α_2 · P_q/K^2$ would here lead to the distorted numerical value $ρ_v = 36.66$.
- This different result is justified in detail on the page "The distortion factor" in the book "Linear and Time Invariant systems", based exactly on the same assumptions made for this exercise.