Difference between revisions of "Aufgaben:Exercise 4.10: Turbo Encoder for UMTS and LTE"
| (4 intermediate revisions by the same user not shown) | |||
| Line 75: | Line 75: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | [[File: | + | [[File:EN_KC_A_4_10c_v3_neu2.png|right|frame|Polynomial division for subtask '''(3)''': $G(D) = (1 + D + D^3) \ / \ (1 + D^2 + D^3)$]] |
'''(1)''' The code parameters are $k = 1$ and $n = 3$ ⇒ code rate $\underline{R = 1/3}$. | '''(1)''' The code parameters are $k = 1$ and $n = 3$ ⇒ code rate $\underline{R = 1/3}$. | ||
*The memory is $\underline{m = 3}$. | *The memory is $\underline{m = 3}$. | ||
| Line 82: | Line 82: | ||
| − | |||
| + | '''(2)''' As the comparison of the "recursive filter" on the data page with the [[Channel_Coding/Algebraic_and_Polynomial_Description#Filter_structure_with_fractional.E2.80.93rational_transfer_function|"filter structure"]] in the theory section for fractional–rational $G(D)$, the <u>proposed solution 1</u> is correct. | ||
| − | |||
| − | The upper graph illustrates the polynomial division $(1 + D + D^3) \ / \ (1 + D^2 + D^3)$. For explanation: | + | |
| − | *Cancelled is the representation with the remainder $D^8 + D^9 = D^7 \cdot (D + D^2)$. | + | '''(3)''' Correct are the <u>proposed solutions 2 and 3</u>: |
| − | + | ||
| − | :$$(D^8 + D^9) \hspace{0.05cm} /\hspace{0.05cm} (1+ D^2+ D^3 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} D^7 \cdot (D+ D^2+ D^3 + D^6) + {\rm | + | The upper graph illustrates the polynomial division $(1 + D + D^3) \ / \ (1 + D^2 + D^3)$. For explanation: |
| + | *Cancelled is the representation with the remainder $D^8 + D^9 = D^7 \cdot (D + D^2)$. Thus also holds: | ||
| + | :$$(D^8 + D^9) \hspace{0.05cm} /\hspace{0.05cm} (1+ D^2+ D^3 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} D^7 \cdot (D+ D^2+ D^3 + D^6) + {\rm remainder_2}$$ | ||
*After summarizing: | *After summarizing: | ||
:$$G(D) = 1 + D + D^2 + D^3 + D^6 + D^8+ D^9+ D^{10} + D^{13} + \hspace{0.05cm}\text{ ... }\hspace{0.05cm} \hspace{0.05cm}. $$ | :$$G(D) = 1 + D + D^2 + D^3 + D^6 + D^8+ D^9+ D^{10} + D^{13} + \hspace{0.05cm}\text{ ... }\hspace{0.05cm} \hspace{0.05cm}. $$ | ||
| Line 112: | Line 113: | ||
* The impulse response continues to infinity ⇒ Solution proposal 3 is also correct. | * The impulse response continues to infinity ⇒ Solution proposal 3 is also correct. | ||
| + | |||
| Line 127: | Line 129: | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | In the state transition diagram (right), the impulse response $\underline{g}$ is highlighted in yellow. The impulse response results as the parity-check sequence $\underline{p}$ for the information sequence $\underline{u} = (1, \, 0, \, 0, \, 0, \, 0, \, \text{ ... })$. | + | *In the state transition diagram $($right$)$, the impulse response $\underline{g}$ is highlighted in yellow. |
| − | * The transitions in the diagram are labeled "$u_i\hspace{0.05cm}|\hspace{0.05cm}\underline{x}_i$", which is equivalent to "$u_i\hspace{0.05cm}|\hspace{0.05cm}u_i \hspace{0.05cm}p_i$". | + | |
| − | *The parity-check sequence $\underline{p} \ (=$ impulse response $\underline{g})$ thus results from the respective second coder output symbol. | + | *The impulse response results as the parity-check sequence $\underline{p}$ for the information sequence $\underline{u} = (1, \, 0, \, 0, \, 0, \, 0, \, \text{ ... })$. |
| − | * $\underline{g}$ is represented by the following states: | + | |
| + | * The transitions in the diagram are labeled "$u_i\hspace{0.05cm}|\hspace{0.05cm}\underline{x}_i$", which is equivalent to "$u_i\hspace{0.05cm}|\hspace{0.05cm}u_i \hspace{0.05cm}p_i$". | ||
| + | |||
| + | *The parity-check sequence $\underline{p} \ (=$ impulse response $\underline{g})$ thus results from the respective second coder output symbol. | ||
| + | |||
| + | * The impulse response $\underline{g}$ is represented by the following states: | ||
:$$S_0 → [S_1 → S_2 → S_5 → S_3 → S_7 → S_6 → S_4 ] → [S_1 → \ ... \ → S_4] → \ \text{ ... } $$ | :$$S_0 → [S_1 → S_2 → S_5 → S_3 → S_7 → S_6 → S_4 ] → [S_1 → \ ... \ → S_4] → \ \text{ ... } $$ | ||
| − | '''(5)''' The following | + | '''(5)''' The following graph shows the solution using the generator matrix $\mathbf{G}$. It holds $\underline{u} = (0, \, 1, \, 1, \, 0, \, 0, \, \text{ ... } )$. |
[[File:EN_KC_A_4_10e_v1.png|right|frame|$\underline{p} = (0, \, 1, \, 1, \, \text{ ... } ) \cdot \mathbf{G}$]] | [[File:EN_KC_A_4_10e_v1.png|right|frame|$\underline{p} = (0, \, 1, \, 1, \, \text{ ... } ) \cdot \mathbf{G}$]] | ||
| − | + | [[File:EN_KC_A_4_10f_v1.png|right|frame|$\underline{p} = (0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 1, \, 0, \, 0, \, \text{ ... }) \cdot \mathbf{G}$]] | |
| − | |||
| − | |||
| − | |||
| + | It can be seen that <u>solutions 1, 2 and 3</u> are correct: | ||
| + | * The present parity-check sequence $\underline{p}$ has the same period $P = 7$ as the impulse response $\underline{g}$. | ||
| − | + | * The Hamming weight of the $($limited$)$ input sequence is actually $w_{\rm H}(\underline{u}) = 2$. | |
| + | * Proposition 4 is incorrect. Rather, for the semi–infinite output sequence: $w_{\rm H}(\underline{p}) → \infty$. | ||
| + | *In the transition diagram, the states | ||
| + | :$$S_0 → S_0 → S_1 → S_3 → S_7 → S_6 → S_4 → S_1$$ | ||
| + | : are passed through first. | ||
| + | *This is followed $($infinitely often$)$ by the periodic portion | ||
| + | :$$S_1 → S_2 → S_5 → S_3 → S_7 → S_6 → S_4 → S_1.$$ | ||
| − | |||
| − | + | '''(6)''' The last graph shows the solution for | |
| + | :$$U(D) = D + D^8$$ | ||
| + | :$$ \Rightarrow \hspace{0.3cm}\underline{u} = (0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 1, \, 0, \, 0, \, \text{ ... }).$$ | ||
| + | *Correct are the <u>proposed solutions 3 and 4</u>: | ||
| + | |||
| + | *The input sequence $\underline{u}$ contains two "ones" and the output sequence $\underline{p}$ six "ones". | ||
| − | + | *From position 10 the output sequence is $\underline{p} \equiv\underline{0}$ <br>⇒ proposals 1 and 2 therefore do not apply. | |
| − | |||
| − | *From position 10 | ||
<br clear=all> | <br clear=all> | ||
| − | + | <u>Further notes:</u> | |
| − | + | # For turbo codes, especially those input sequences $\underline{u}$ whose $D$–transforms are representable as $U(D) = f(D) \cdot [1 + D^{P}]$ are extremely unfavorable. | |
| − | + | #They cause the error floor as seen on the [[Channel_Coding/The_Basics_of_Turbo_Codes#Performance_of_the_turbo_codes|"Performance of Turbo Codes"]] page in the theory section. | |
| − | + | #$P$ indicates here the period of the impulse response $\underline{g}$. In our example $f(D) = D$ and $P = 7$. | |
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 16:11, 22 December 2022
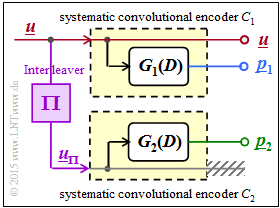
The mobile communications standards $\rm UMTS$ and $\rm LTE$ each use a turbo code that is largely identical to the encoder described in the "The Basics of Turbo Codes" chapter.
- The $1/n$ convolutional code is systematic, meaning that the encoded sequence $\underline{x}$ includes the information sequence $\underline{u}$ as a component.
- The parity-check sequences $\underline{p}_1$ and $\underline{p}_2$ are based on the same transfer function:
- $$G_1(D) = G_2(D) = G(D).$$
- $\underline{p}_1$ and $\underline{p}_2$ however, use different input sequences $\underline{u}$ and $\underline{u}_{\pi}$, respectively. Here, ${\rm \Pi}$ marks the interleaver, for UMTS and LTE mostly a $S$–random interleaver.
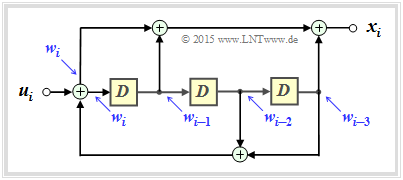
The main difference compared to the description in the theory part results from a different transfer function $G(D)$ given by the recursive filter structure drawn on the left.
Hints:
- The exercise belongs to the chapter "Basics of Turbo Codes".
- Knowledge is expected about
- For further guidance on how to do this, see $\text{Exercise 4.8}$ and $\text{Exercise 4.9}$.
- The information sequence $\underline{u}$ is partially specified by its $D$–transform for easier description in the subtasks. For example:
- $$\underline{u}= (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}\hspace{0.05cm} \text{...}\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = D+ D^2\hspace{0.05cm},$$
- $$\underline{u}= (\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm}\hspace{0.05cm} \text{...}\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = D+ D^8\hspace{0.05cm}.$$
Questions
Solution
(1) The code parameters are $k = 1$ and $n = 3$ ⇒ code rate $\underline{R = 1/3}$.
- The memory is $\underline{m = 3}$.
- The influence lengths result in $\nu = 1, \ \nu_2 = 4$ and $\nu_3 = 4$ ⇒ Total influence length $\underline{\nu = 9}$.
(2) As the comparison of the "recursive filter" on the data page with the "filter structure" in the theory section for fractional–rational $G(D)$, the proposed solution 1 is correct.
(3) Correct are the proposed solutions 2 and 3:
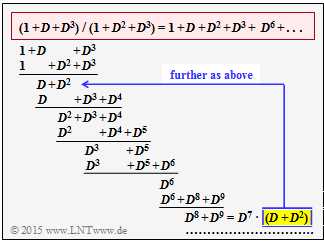
The upper graph illustrates the polynomial division $(1 + D + D^3) \ / \ (1 + D^2 + D^3)$. For explanation:
- Cancelled is the representation with the remainder $D^8 + D^9 = D^7 \cdot (D + D^2)$. Thus also holds:
- $$(D^8 + D^9) \hspace{0.05cm} /\hspace{0.05cm} (1+ D^2+ D^3 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} D^7 \cdot (D+ D^2+ D^3 + D^6) + {\rm remainder_2}$$
- After summarizing:
- $$G(D) = 1 + D + D^2 + D^3 + D^6 + D^8+ D^9+ D^{10} + D^{13} + \hspace{0.05cm}\text{ ... }\hspace{0.05cm} \hspace{0.05cm}. $$
- The $D$–inverse transform gives the proposed solution 2:
- $$\underline{g}= (\hspace{0.05cm}1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{ ... }\hspace{0.05cm})\hspace{0.05cm}. $$
- The impulse response continues to infinity ⇒ Solution proposal 3 is also correct.
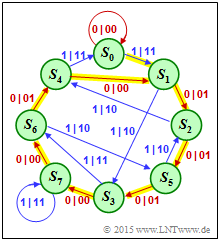
(4) The impulse response can be expressed as follows:
- $$\underline{g}= \Big (\hspace{0.03cm}1\hspace{0.03cm}, \big [ \hspace{0.03cm} 1\hspace{0.03cm}, \hspace{0.03cm} 1\hspace{0.03cm}, \hspace{0.03cm} 1\hspace{0.03cm}, \hspace{0.03cm} 0\hspace{0.03cm}, \hspace{0.03cm} 0\hspace{0.03cm}, \hspace{0.03cm} 1\hspace{0.03cm}, \hspace{0.03cm} 0\hspace{0.03cm} \big ]_{\rm per} \Big ) \hspace{0.15cm}\Rightarrow \hspace{0.15cm} \underline{P = 7} \hspace{0.05cm}. $$
- In the state transition diagram $($right$)$, the impulse response $\underline{g}$ is highlighted in yellow.
- The impulse response results as the parity-check sequence $\underline{p}$ for the information sequence $\underline{u} = (1, \, 0, \, 0, \, 0, \, 0, \, \text{ ... })$.
- The transitions in the diagram are labeled "$u_i\hspace{0.05cm}|\hspace{0.05cm}\underline{x}_i$", which is equivalent to "$u_i\hspace{0.05cm}|\hspace{0.05cm}u_i \hspace{0.05cm}p_i$".
- The parity-check sequence $\underline{p} \ (=$ impulse response $\underline{g})$ thus results from the respective second coder output symbol.
- The impulse response $\underline{g}$ is represented by the following states:
- $$S_0 → [S_1 → S_2 → S_5 → S_3 → S_7 → S_6 → S_4 ] → [S_1 → \ ... \ → S_4] → \ \text{ ... } $$
(5) The following graph shows the solution using the generator matrix $\mathbf{G}$. It holds $\underline{u} = (0, \, 1, \, 1, \, 0, \, 0, \, \text{ ... } )$.
It can be seen that solutions 1, 2 and 3 are correct:
- The present parity-check sequence $\underline{p}$ has the same period $P = 7$ as the impulse response $\underline{g}$.
- The Hamming weight of the $($limited$)$ input sequence is actually $w_{\rm H}(\underline{u}) = 2$.
- Proposition 4 is incorrect. Rather, for the semi–infinite output sequence: $w_{\rm H}(\underline{p}) → \infty$.
- In the transition diagram, the states
- $$S_0 → S_0 → S_1 → S_3 → S_7 → S_6 → S_4 → S_1$$
- are passed through first.
- This is followed $($infinitely often$)$ by the periodic portion
- $$S_1 → S_2 → S_5 → S_3 → S_7 → S_6 → S_4 → S_1.$$
(6) The last graph shows the solution for
- $$U(D) = D + D^8$$
- $$ \Rightarrow \hspace{0.3cm}\underline{u} = (0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 1, \, 0, \, 0, \, \text{ ... }).$$
- Correct are the proposed solutions 3 and 4:
- The input sequence $\underline{u}$ contains two "ones" and the output sequence $\underline{p}$ six "ones".
- From position 10 the output sequence is $\underline{p} \equiv\underline{0}$
⇒ proposals 1 and 2 therefore do not apply.
Further notes:
- For turbo codes, especially those input sequences $\underline{u}$ whose $D$–transforms are representable as $U(D) = f(D) \cdot [1 + D^{P}]$ are extremely unfavorable.
- They cause the error floor as seen on the "Performance of Turbo Codes" page in the theory section.
- $P$ indicates here the period of the impulse response $\underline{g}$. In our example $f(D) = D$ and $P = 7$.