Difference between revisions of "Mobile Communications/General Description of Time Variant Systems"
m (Text replacement - "[[Lineare_zeitinvariante_Systeme/" to "[[Linear_and_Time_Invariant_Systems/") |
|||
| Line 31: | Line 31: | ||
The most important results are briefly explained again here.<br> | The most important results are briefly explained again here.<br> | ||
| − | We assume a ''linear and time invariant system'' ⇒ ''' | + | We assume a ''linear and time invariant system'' ⇒ '''LTI–System''' with the signal $s(t)$ at the input and the output signal $r(t)$. For the sake of simplicity, let $s(t)$ and $r(t)$ be real. Then the following applies: |
*The system can be completely characterized by the [[Linear_and_Time_Invariant_Systems/Systembeschreibung_im_Frequenzbereich#.C3.9Cbertragungsfunktion_-_Frequenzgang|transfer function]] $H(f)$ Which is also referred to as the <i> Frequency response</i>. By definition :$$H(f) = R(f)/S(f).$$ | *The system can be completely characterized by the [[Linear_and_Time_Invariant_Systems/Systembeschreibung_im_Frequenzbereich#.C3.9Cbertragungsfunktion_-_Frequenzgang|transfer function]] $H(f)$ Which is also referred to as the <i> Frequency response</i>. By definition :$$H(f) = R(f)/S(f).$$ | ||
| Line 98: | Line 98: | ||
The following relations apply: | The following relations apply: | ||
| − | ::<math>\text{ | + | ::<math>\text{LTI:}\hspace{0.5cm} r(t) = \int_{-\infty}^{+\infty} h(\tau) \cdot s(t-\tau) \hspace{0.15cm}{\rm d}\tau \hspace{0.05cm},</math> |
| − | ::<math>\text{ | + | ::<math>\text{LTV:}\hspace{0.5cm} r(t) \hspace{-0.1cm} = \hspace{-0.1cm} \int_{-\infty}^{+\infty} h(\tau, \hspace{0.1cm}t) \cdot s(t-\tau) \hspace{0.15cm}{\rm d}\tau \hspace{0.05cm}.</math> |
<br clear=all> | <br clear=all> | ||
Regarding the last equation and the above graph, it should be noted | Regarding the last equation and the above graph, it should be noted | ||
| − | *The parameter $\tau$ specifies the '''Delay time''' to denote the time dispersion. By writing out the convolution operation, it was possible to make $\tau$ also the parameter of the | + | *The parameter $\tau$ specifies the '''Delay time''' to denote the time dispersion. By writing out the convolution operation, it was possible to make $\tau$ also the parameter of the LTI–impulse response. On the last pages we spoke about $h(t)$ .<br> |
*The second parameter of the impulse response or the second axis marks the '''absolute time''' $t$, which is used, among other things, to describe the time variance. At different times $t$ the impulse response $h(\tau, \hspace{0.05cm}t)$ has a different form.<br> | *The second parameter of the impulse response or the second axis marks the '''absolute time''' $t$, which is used, among other things, to describe the time variance. At different times $t$ the impulse response $h(\tau, \hspace{0.05cm}t)$ has a different form.<br> | ||
Revision as of 17:00, 11 July 2020
Contents
# SYNOPSIS TO SECOND MAIN CHAPTER #
After the time variance, the term frequency selectivity is now introduced and illustrated with examples, a channel property which is also of great importance for mobile communication. As in the entire book, the description is given in the equivalent low-pass range.
It is covered in detail:
- the difference between time invariant and time variant systems,
- the time variant impulse response as an important descriptive function of time variant systems,
- multi-way reception as the cause of frequency-selective behaviour,
- a detailed derivation and interpretation of the GWSSUS channel model,
- the characteristics of the GWSSUS model: coherence bandwidth, correlation duration, etc.
Transfer function and impulse response
The description parameters of a message transmission system have already been described in the chapters
of the book "Linear Time Variant Systems".
The most important results are briefly explained again here.
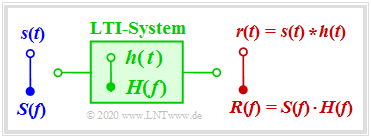
We assume a linear and time invariant system ⇒ LTI–System with the signal $s(t)$ at the input and the output signal $r(t)$. For the sake of simplicity, let $s(t)$ and $r(t)$ be real. Then the following applies:
- The system can be completely characterized by the transfer function $H(f)$ Which is also referred to as the Frequency response. By definition :$$H(f) = R(f)/S(f).$$
- Similarly, the system is defined by the Impulse response $h(t)$ , which is the inverse Fourier transformation of $H(f)$ The output signal results from the convolution:
- \[r(t) = s(t) \star h(t) \hspace{0.4cm} {\rm mit} \hspace{0.4cm} h(t) \hspace{0.2cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.2cm} H(f) \hspace{0.05cm}.\]
$\text{Definitions:}$
The following input signals are suitable for detecting the linear distortions caused by $H(f)$ or $h(t)$
- $$s(t) = \delta(t) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} r(t) = \delta(t) \star h(t)= h(t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \text{Impulse response,}$$
- $$s(t) = \gamma(t) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} r(t) = \gamma(t) \star h(t)\hspace{1.5cm}\Rightarrow \hspace{0.3cm} \text{step response,}$$
- $$s(t) = p_\delta(t) \hspace{0.25cm}\Rightarrow \hspace{0.3cm} r(t) = p_\delta(t) \star h(t)\hspace{1.3cm}\Rightarrow \hspace{0.3cm} \text{impulse response train.}$$
On the other hand, a DC signal $s(t) = A$ is not suitable to make the frequency dependence of the LTI system visible:
With a low-pass system the output signal would then be always constant, independent of $H(f)$ $r(t) = A \cdot H(f= 0)$.
On the next page we consider a Dirac impulse train $p_\delta(t)$ as an input signal $s(t)$ :
Hereby the similarities and differences between time-invariant and time-variant systems can be shown clearly.
Note: The properties of $H(f)$ and $h(t)$ are covered in detail in the learning video Some remarks on the transfer function .
Time invariant vs. time variant channels
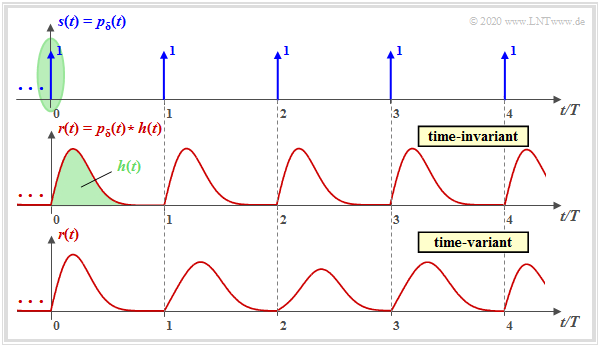
The graphic is intended to illustrate the difference between a time invariant channel $\rm (LTI)$ and a time variant channel $\rm (LTV)$ .
One can see from this illustration:
- The transmitted signal $s(t)$ is a Dirac impulse train $p_\delta(t)$, i.e. an infinite sequence of Dirac impulses in equidistant intervals $T$, all with the weight $1$ (see upper graph):
- \[s(t) = p_{\rm \delta} (t) = \sum_{n = -\infty}^{+\infty} {\rm \delta} (t - n \cdot T) \hspace{0.05cm}.\]
- The Dirac impulse at $t = 0$ is marked in green. The signal at the channel output is equal to $r(t) = h(t)$ , with $s(t) = {\rm \delta}(t)$ , also indicated in green. As a condition, it is assumed that the extension of the impulse response $h(t)$ is smaller than $T$.
.
- The entire received signal after the LTI channel, according to the middle graph, can then be written as:
- \[r(t) = p_{\rm \delta} (t) \star h(t) = \sum_{n = -\infty}^{+\infty} h (t - n \cdot T) \hspace{0.05cm}.\]
- For a time-variant channel (lower graph) this equation is not applicable. In each time interval, a (slightly) different signal shape is obtained.
$\text{Conclusion:}$ With a time-variant channel you cannot specify neither a one-parameter impulse response $h(t)$ nor a transfer function $H(f)$ .
Note: The learning video Properties of the transmission channel describes the differences between LTI and LTV systems.
Two-dimensional impulse response
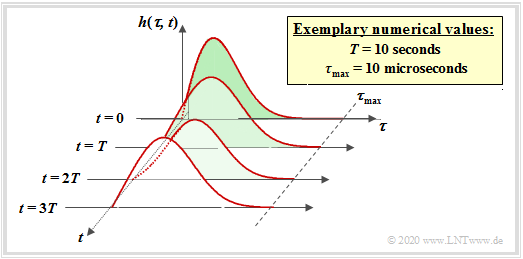
To identify a time-variant impulse response, a second parameter is used and the impulse response is preferably mapped in a three-dimensional coordinate system.
The condition for this is that the channel is still linear; one speaks then of a $\rm LTV System$ ("linear time-variant").
The following relations apply:
- \[\text{LTI:}\hspace{0.5cm} r(t) = \int_{-\infty}^{+\infty} h(\tau) \cdot s(t-\tau) \hspace{0.15cm}{\rm d}\tau \hspace{0.05cm},\]
- \[\text{LTV:}\hspace{0.5cm} r(t) \hspace{-0.1cm} = \hspace{-0.1cm} \int_{-\infty}^{+\infty} h(\tau, \hspace{0.1cm}t) \cdot s(t-\tau) \hspace{0.15cm}{\rm d}\tau \hspace{0.05cm}.\]
Regarding the last equation and the above graph, it should be noted
- The parameter $\tau$ specifies the Delay time to denote the time dispersion. By writing out the convolution operation, it was possible to make $\tau$ also the parameter of the LTI–impulse response. On the last pages we spoke about $h(t)$ .
- The second parameter of the impulse response or the second axis marks the absolute time $t$, which is used, among other things, to describe the time variance. At different times $t$ the impulse response $h(\tau, \hspace{0.05cm}t)$ has a different form.
- A peculiarity of the 2D representation is that the $t$–axis is always plotted time-discretely $($at multiples of $T)$ while the $\tau$–axis can be continuous in time as in the example shown. However, in mobile communications, a time-discrete $h(\tau, \hspace{0.05cm}t_0)$ with respect to $\tau$ is assumed $($„echoes”$)$.
- The LTV–equation is only applicable if the time change of the channel is slow in comparison to the maximum delay $\tau_{\rm max}$ $($marked in the figure by the parameter $T$ $)$. In mobile communications this condition ⇒ $\tau_{\rm max} < T$ is almost always fulfilled.
- Selecting whether to apply the first Fourier integral to the parameter $\tau$ or $t$ leads to different spectral functions. In the Excercise 2.1Z for example, the time variant 2D–Transfer function is considered:
- \[H(f,\hspace{0.05cm} t) \hspace{0.2cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) \hspace{0.05cm}.\]
Excercises to the chapter
Exercise 2.1: Two-Dimensional Impulse Response
Exercise 2.1Z: 2D-Frequency and 2D-Time Representations