Difference between revisions of "Modulation Methods/Frequency Modulation (FM)"
m |
m |
||
| Line 229: | Line 229: | ||
[[File:EN_Mod_T_3_2_S7.png|right|frame| PLL Realization of a FM demodulator]] | [[File:EN_Mod_T_3_2_S7.png|right|frame| PLL Realization of a FM demodulator]] | ||
| − | * | + | *The phase detector determines the phase differences (distances of zero intercepts) between the received signal $r(t)$ and the comparison signal provided by the VCO. |
| − | * | + | *After low-pass filtering and amplification, the output signal $v(t)$ is approximately equal to the source signal $q(t)$ if it has been FM-modulated at the transmit end. |
| − | * | + | *The output signal $v(t)$ is simultaneously applied to the input of the ''Voltage Controlled Oscillator,'', abbreviated as $\rm VCO$. |
| − | * | + | *The output signal of the VCO is permanently readjusted in such a way that its frequency corresponds as closely to the instantaneous frequency $f_{\rm A}(t)$ of the received signal $r(t)$ . |
Revision as of 12:43, 17 March 2022
Contents
- 1 Instantaneous frequency
- 2 Signal characteristics with frequency modulation
- 3 Frequency modulation of a cosine signal
- 4 WM spectrum of a harmonic oscillation
- 5 Influence of band-limiting in angle modulation
- 6 Realization of a FM modulator
- 7 PLL Realization of FM demodulator
- 8 Aufgaben zum Kapitel
- 9 Quellenverzeichnis
Instantaneous frequency
We will once again assume an angle-modulated signal:
- $$s(t) = A_{\rm T} \cdot \cos \big[\psi(t)\big].$$
All the information about the source signal $q(t)$
- is thus exclusively captured by the angular function $ψ(t)$ ,
- while the envelope $a(t) = A_{\rm T}$ is constant.
$\text{Definitions:}$
- The instantaneous angular frequency is the derivative of the angular function with respect to time:
- $$\omega_{\rm A}(t) = \frac{ {\rm d}\psi(t)}{ {\rm d}t}\hspace{0.05cm}.$$
- Accordingly, the instantaneous frequency is described by:
- $$f_{\rm A}(t) = \frac{\omega_{\rm A}(t)}{2\pi} = \frac{1}{2\pi} \cdot \frac{ {\rm d}\hspace{0.03cm}\psi(t)}{ {\rm d}t}\hspace{0.05cm}.$$
- The frequency deviation is the maximum deviation $Δf_{\rm A}$ of the time-dependent instantaneous frequency $f_{\rm A}(t)$ from the constant carrier frequency $f_{\rm T}$.
For an angle modulation with carrier frequency $f_{\rm T}$ , the instantaneous frequency oscillates in the range
- $$f_{\rm T} - \Delta f_{\rm A} \le f_{\rm A}(t) \le f_{\rm T} + \Delta f_{\rm A}\hspace{0.05cm}.$$
It should be emphasized that there is a fundamental difference between the instantaneous frequency $f_{\rm A}(t)$ and the spectrum $S(f)$ of an angle-modulated signal $s(t)$ that can be measured with a spectrum analyzer, as illustrated by the following example.
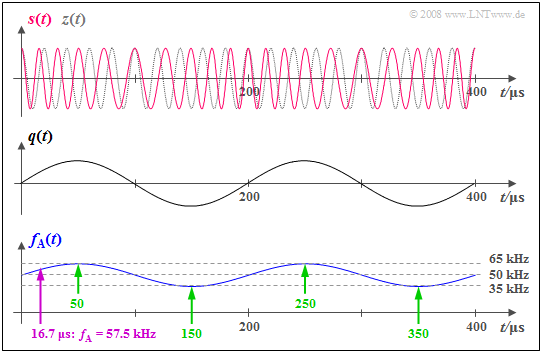
$\text{Example 1:}$ The graph shows the phase-modulated signal
- $$s(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[\psi(t)\big] = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[2 \pi f_{\rm T} \hspace{0.05cm}t + \eta \cdot \sin (2 \pi f_{\rm N} \hspace{0.05cm} t)\big]$$
as well as the instantaneous frequency plotted beneath
- $$f_{\rm A}(t) = \frac{1}{2 \pi} \cdot \frac{ {\rm d}\hspace{0.03cm}\psi(t)}{ {\rm d}t} = f_{\rm T} + \Delta f_{\rm A}\cdot \cos (2 \pi f_{\rm N} \hspace{0.05cm} t) \hspace{0.05cm}.$$
Here, the system parameters are:
- $f_{\rm T} = 50 \ \rm kHz$,
- $f_{\rm N} = 5 \ \rm kHz$,
- $η = 3$.
From this, we derive the frequency deviation
- $Δf_{\rm A} = η · f_{\rm N} = 15 \ \rm kHz$.
In the middle, the qualitative progression of the sinusoidal source signal $q(t)$ is sketched for reference.
From these graphs, one can see:
- The instantaneous frequency $f_{\rm A}(t)$ can take on arbitrary values between $f_{\rm T} + Δf_{\rm A} = 65 \ \rm kHz$ $($at $t = 50\ \rm µ s,\ 250 \ µ s$, etc.$)$ and $f_{\rm T} \ – Δf_{\rm A} = 35 \ \rm kHz$ $($at $t = 150\ \rm µ s, \ 350 \ µ s$, etc.$)$ (see green marks).
- At time $t ≈ 16.7 \ \rm µ s$ , for example, $f_{\rm A}(t) = 57.5 \ \rm kHz$ holds (purple arrow).
- In contrast, the spectral function $S(f)$ consists of discrete Bessel lines at the frequencies ... , $30,\ 35,\ 40,\ 45,\ \mathbf{50},\ 55,\ 60,\ 65,\ 70$, ... $($each in $\rm kHz)$.
- There is no spectral line at $f = 57.5 \ \rm kHz$ , though there is one at $f = 70 \ \rm kHz$.
- In contrast, at no time does $f_{\rm A}(t) = 70 \ \rm kHz$ hold.
$\text{Therefore:}$
The instantaneous frequency $f_{\rm A}(t)$ is thus not a physically measurable frequency in the conventional sense, but only an abstract mathematical quantity, namely the derivative of the angular function $ψ(t)$.
Signal characteristics with frequency modulation
As in the chapter Phase Modulation we will assume that the carrier signal $z(t)$ has a cosine waveform and the source signal $q(t)$ is peak-limited.
$\text{Definition:}$ In a communication system, if the instantaneous angular frequency $ω_{\rm A}(t)$ is linearly dependent on the instantaneous value of the source signal $q(t)$, we call this frequency modulation $\rm (FM)$:
- $$\omega_{\rm A}(t) = 2 \pi \cdot f_{\rm A}(t) = \omega_{\rm T} + K_{\rm FM} \cdot q(t) \hspace{0.05cm}.$$
Here, $K_{\rm FM}$ denotes a dimensionally restricted constant. If $q(t)$ represents a voltage waveform, $K_{\rm FM}$ has the unit $\rm V^{–1}s^{–1}$.
In frequency modulation, the angular function $\psi(t)$ and the modulated signal $s(t)$ are given by:
- $$\psi(t) = \omega_{\rm T} \cdot t + K_{\rm FM} \cdot \int q(t)\hspace{0.1cm}{\rm d}t \hspace{0.05cm}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}s(t) = A_{\rm T} \cdot \cos \big[\psi(t)\big] \hspace{0.05cm}.$$
From this equation, we can immediately see:
- Even in the case of frequency modulation, the equivalent low-pass signal moves on an arc because of the constant envelope ⇒ $a(t) = A_{\rm T}$ .
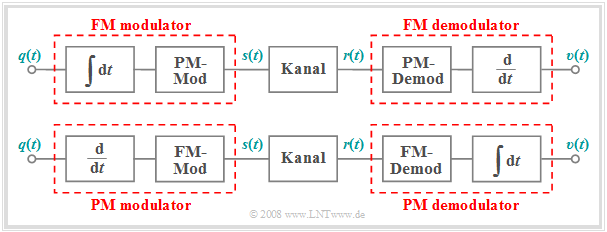
- A frequency modulator can be implemented using an integrator and a phase modulator. Consequently, the FM demodulator consists of a PM demodulator and a differentiator, as shown in the upper part of the following diagram.
The lower graph shows the inverse relationship ⇒ a possible description of a PM modulator and demodulator in terms of corresponding FM components.
It can also be seen from the above equation, that the equation encountered earlier on page A very simple (though unfortunately not always correct) modulator equation in the first chapter of this book, will only hold for frequency modulation in very special cases.
In frequency modulation, the conversion
- $$s(t) = a(t) \cdot \cos (\omega (t) \cdot t + \phi(t)) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} s(t) = A_{\rm T} \cdot \cos (\omega (t) \cdot t + \phi_{\rm T})$$
is only allowed sometimes, such as in the nonlinear digital modulation method "Frequency Shift Keying" $\rm (FSK)$ with a right-angled fundamental pulse.
Frequency modulation of a cosine signal
For a cosine source signal $q(t)$ with frequency modulation, the instantaneous angular frequency is:
- $$q(t) = A_{\rm N} \cdot \cos (\omega_{\rm N} \cdot t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \omega_{\rm A}(t) = \omega_{\rm T} + K_{\rm FM} \cdot A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t)\hspace{0.05cm}.$$
Integrating this over time, we get the angular function:
- $$\psi(t) = \omega_{\rm T} \cdot t + \frac {K_{\rm FM} \cdot A_{\rm N}}{\omega_{\rm N}} \cdot \sin (\omega_{\rm N} \cdot t) \hspace{0.05cm}.$$
A comparison with the propositions in the chapter Phase Modulation makes clear:
- The frequency modulation of a cosine signal yields a qualitatively identical transmitted signal $s(t)$ as the phase modulation of a sinusoidal source signal $q(t)$.
- However, this requires that the modulator constants are matched according to the ratio $K_{\rm FM}/K_{\rm PM} = ω_{\rm N}$ .
- The transmitted signal $s(t)$ can thus be described uniformly for the two configurations "PM – sine signal" as well as "FM – cosine signal":
- $$s(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[\omega_{\rm T} \cdot t + \eta \cdot \sin (\omega_{\rm N} \cdot t)\big] \hspace{0.05cm}.$$
- However, when using this equation for the modulation index $η$ different equations must be use for phase and frequency modulation:
- $$\eta_{\rm PM} = {K_{\rm PM} \cdot A_{\rm N}},$$
- $$\eta_{\rm FM} = \frac {K_{\rm FM} \cdot A_{\rm N}}{\omega_{\rm N}} \hspace{0.05cm}.$$
- If the source signal is not a harmonic oscillation, but is instead composed of several frequencies, the time signals also differ qualitatively for phase and frequency modulation. This can be seen in the earlier comparison of PSK and FSK.
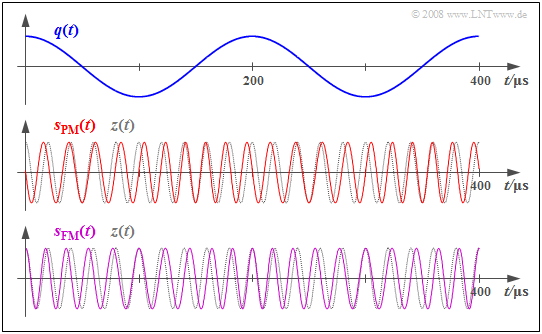
$\text{Example 2:}$ We will now assume a cosine source signal $q(t)$ with amplitude $A_{\rm N} = 3 \ \rm V$ and frequency $f_{\rm N} = 5 \ \rm kHz$ and consider the signal characteristics of phase modulation $\rm (PM)$ and frequency modulation $\rm (FM)$ with the same modulation index $η = 1.5$.
Thee middle graph shows the phase-modulated signal (rote curve) for the modulator parameters $f_{\rm T} = 50 \ \rm kHz$ und $K_{\rm PM} = \rm 0.5 V^{–1}$:
- $$s_{\rm PM}(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[\omega_{\rm T} \cdot t + \eta \cdot \cos (\omega_{\rm N} \cdot t)\big ] \hspace{0.05cm}.$$
- In phase modulation, $A_{\rm N} = 3 \ \rm V$ yields $η = 1.5 ≈ π/2$ for the phase deviation (modulation index).
- The maximum deviation of the zero crossings from their (equidistant) nominal positions is about a quarter of the carrier period.
- If the source signal is $q(t) > 0$, the zero crossings arrive early, and if $q(t) < 0$ , they come late.
The lower graph shows the frequency-modulated signal with the same modulation index $η$:
- $$s_{\rm FM}(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm} \big[\omega_{\rm T} \cdot t + \eta \cdot \sin (\omega_{\rm N} \cdot t)\big ] \hspace{0.05cm}.$$
In this case, $η = 1.5$ is achieved by the modulator constant
- $$K_{\rm FM} = \frac {\eta \cdot \omega_{\rm N} }{A_{\rm N} } = {K_{\rm PM} \cdot \omega_{\rm N} } $$
- $$\Rightarrow \hspace{0.3cm} K_{\rm FM} = 0.5\,{\rm V}^{-1} \cdot 2 \pi \cdot 5\,{\rm kHz} = 15708\,{\rm V}^{-1}{\rm s}^{-1} \hspace{0.05cm}.$$
- Here, the frequency deviation is $Δf_{\rm A} = η · f_{\rm N} = 7.5 \ \rm kHz$, and instantaneous frequencies occur between $f_{\rm T}-Δf_{\rm A} = 42.5$ and $f_{\rm T}+Δf_{\rm A} =57.5 \ \rm kHz$ .
- the zero crossings now match those of the carrier signal $z(t)$ at the maxima and minima of the source signal $q(t)$ , while the maximum phase deviations can be seen at the zero crossings of $q(t)$ . The exact opposite is the case in phase modulation.
WM spectrum of a harmonic oscillation
Now we assume a harmonic oscillation with phase $ϕ_{\rm N}$ for the source signal in general:
- $$q(t) = A_{\rm N} \cdot \cos \hspace{-0.1cm} \big[2 \pi f_{\rm N} \cdot t + \phi_{\rm N}\big ].$$
We are interested in the spectral function $S(f)$. For simplicity, the following will consider the magnitude spectrum $|S_+(f)|$ of the analytical signal, from which $|S(f)|$ can be derived in the familiar way.
For any of the types of angle modulation described here – whether it is phase or frequency modulation – and regardless of the phase $ϕ_{\rm N}$ of the source signal, the following holds:
- $$|S_{\rm +}(f)| = A_{\rm T} \cdot \sum_{n = - \infty}^{+\infty}|{\rm J}_n (\eta)| \cdot \delta \big[f - (f_{\rm T} + n \cdot f_{\rm N})\big]\hspace{0.05cm}.$$
This equation can be explained as follows:
- On the page equivalent low-pass signal in PM this equation was derived for a phase-modulated sine signal, where $η = A_{\rm N} · K_{\rm PM}$ denotes the modulation index and ${\rm J}_n(η)$ denotes the $n$–th order Bessel functions of the first kind. $K_{\rm PM}$ is the modulator constant.
- When the message phase $ϕ_{\rm N}$ changes, only the phase function ${\rm arc} \ S_+(f)$ changes, but not the magnitude spectrum $|S_+(f)|$. This important result is confirmed in Exercise 3.3Z .
- On the Frequency modulation of a cosine signal page, it was shown that a frequency-modulated signal can be represented in the same way as a phase-modulated signal if the modulation index $η = K_{\rm FM} · A_{\rm N}/ω_{\rm N}$ is used. Consequently, the magnitude spectra for and frequency modulation can also be represented in the same way.
Here we would like to refer you to the second part of the tutorial video Angle modulation – Frequency and phase modulation (currently available in German).
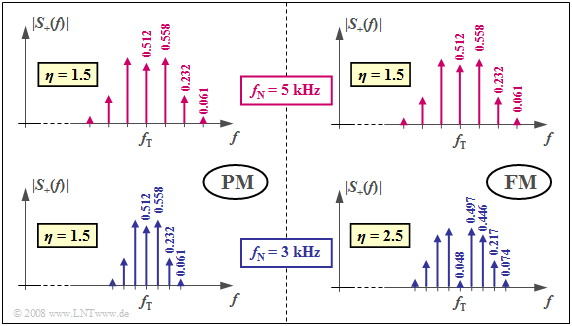
$\text{Example 3:}$ Let us again consider a harmonic oscillation, this time with amplitude $A_{\rm N} = 3 \ \rm V$ according to
- a phase modulation with $K_{\rm PM} = \rm 0.5 \ \rm V^{–1}$,
- a frequency modulation with $K_{\rm FM} = \rm 15708 \ \rm V^{–1}s^{–1}$.
The corresponding signal characteristics are shown in $\text{Example 2}$ .
- For both transmission systems, a Bessel spectrum with modulation index $η = 1.5$ is obtained for $f_{\rm N} = 5 \ \rm kHz$ .
- The identical magnitude spectra of the analytical signal (positive frequencies only) are shown in the two upper graphs .
- Bessel lines with values smaller than $0.03$ are ignored in both cases.
The lower graphs are valid for the message frequency $f_{\rm N} = 3 \ \rm kHz$:
- In phase modulation, there is now a narrower spectral function compared to $f_{\rm N} = 5 \ \rm kHz$ , since the spacing of the Bessel lines is only $3 \ \rm kHz$ (lower graph on the left).
- Since the modulation index $η = 1.5$ does not changes, we get the same Bessel weights as for $f_{\rm N} = 5 \ \rm kHz$ (upper graph).
- Also in frequency modulation, the Bessel lines now occur at $3 \ \rm kHz$ spacing (lower graph on the right).
- However, there are significantly more Bessel lines than in the upper right graph (valid for $η = 1.5$ ) due to the larger modulation index $η = 2.5$ .
- This follows from the fact that for frequency modulation, $η$ is inversely proportional to $f_{\rm N}$ .
Influence of band-limiting in angle modulation
Let us briefly summarize some previous results of this section, by assuming an example with a carrier frequency $f_{\rm T} = 100 \ \rm kHz$, a message frequency $f_{\rm N} = 5 \ \rm kHz$ and a modulation index $η = π/2 \approx 1.5$ :
- The spectrum of an angle-modulated oscillation consists of Bessel lines around the carrier frequency $f_{\rm T}$ at a distance $f_{\rm N}$ from the message frequency and is infinitely extended in theory.
- Even if we ignore all spectral lines with magnitudes smaller than $0.01$ , the now finite bandwidth for $η = π/2$ is still $B_{\rm HF} = 8 · f_{\rm N} = 40 \ \rm kHz$.
- The locus curve – i.e.m the course of the equivalent low-pass signal in the complex plane – is ideally a circular arc with an opening angle of $±1.57 \ {\rm rad} = ±90^\circ$.
- However, this circular arc after vector summation results only if all Bessel lines on the locus rotate with the correct pointer lengths, the correct phase positions and the correct angular frequencies.
- Logically, the circular locus curve is altered when the spectral lines are distorted (for example, by linear channel distortions) or missing altogether (for example, by band-limiting).
- Since the ideal angle demodulator detects the phase $ϕ_r(t)$ of the received signal and obtains the sink signal $v(t)$ from it, this distorts it, even non-linearly. This means: The distortions are irreversible and cannot be compensated for by a linear filter.
- At the same time, this means: due to linear distortions in the channel, nonlinear distortions occur in the demodulated signal $v(t)$ ⇒ as a result, new frequencies (harmonics), are created, which were not in the original source signal $q(t)$ .
- The smaller the available bandwidth $B_{\rm HF}$ is and the larger is the chosen modulation index $η$ , the larger the distortion factor $K$ - which captures nonlinear distortions - becomes . As a rule of thumb for the required RF bandwidth for a desired distortion factor $K$ one can use the so-called "Carson Rule":
- $$K < 10\%\text{:}\hspace{0.6cm} B_{\rm HF} \ge 2 \cdot f_{\rm N} \cdot (\eta +1)\hspace{0.05cm},$$
- $$K < 1\%\text{:}\hspace{0.72cm} B_{\rm HF} \ge 2 \cdot f_{\rm N} \cdot(\eta +2)\hspace{0.05cm}.$$
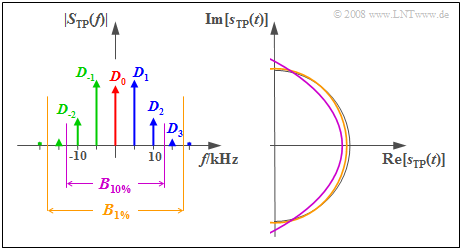
$\text{Example 4:}$ We continue to assume the system parameters $f_{\rm T} = 100 \ \rm kHz$, $f_{\rm N} = 5 \ \rm kHz$ and $η = π/2$ . For this case, the graph displays the magnitude spectrum $ \vert S_{\rm TP}(f) \vert$ of the equivalent low-pass signal on the left and the corresponding complex time function $s_{\rm TP}(t)$ on the right.
- According to Carson's rule, to limit the harmonic distortion to the range $K < 1\%$ , an RF bandwidth of $B_{1 \%} ≈ 36 \ \rm kHz$ is required.
- The equivalent low-pass signal is then composed of the constant $D_0$ and three clockwise $(D_1, D_2, D_3)$ and three counterclockwise $(D_{-1}, D_{-2}, D_{-3})$ rotating pointers:
- $$\begin{align*}s_{\rm TP}(t) & = \sum_{n = - 3}^{+3}D_n \cdot{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.02cm}\cdot \hspace{0.05cm} t }\end{align*}$$
- The ochre curve in the time domain plot makes it clear that the equivalent low-pass signal differs only slightly from the distortion-free semicircle (thin black line) due to this bandwidth limitation.
If one is satisfied with a distortion factor $K < 10\%$ , the RF bandwidth $B_{10 \%} ≈ 26\ \rm kHz$ is already sufficient.
- This also truncates the two Fourier coefficients $D_3$ and $D_{-3}$ and so the locus curve shown in purple represents a section of a parabola.
- The simulation of this case study yields a distortion factor of $K ≈ 6\%$.
- Evidently, Carson's Rule often gives a somewhat too pessimistic result $(10\%$ instead of $6\%)$.
Realization of a FM modulator
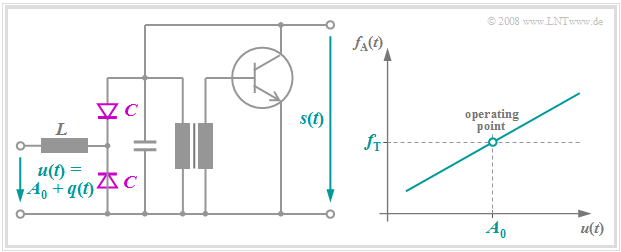
A frequency modulation is obtained when the oscillation frequency of an oscillator is changed to the rhythm of the modulating signal. RC elements or oscillating circuits usually serve as frequency-determining elements. The left graph shows the form of a possible circuit realization; the exact circuit description can be found in [Mäu 88][1]. The idealized frequency-voltage characteristic is shown on the right.
A few remarks should be made here:
- The applied voltage $u(t)$ is additively composed of the source signal $q(t)$ and a DC component $A_0$ which defines the operating point .
- The capacitance $C$ of the capacitance diode is approximately proportional to $1/u^{2}(t)$, , so the oscillation frequency of the LC oscillator changes depending on $q(t)$ .
- When the change in frequency is small, $u(t)$ and $f_{\rm A}(t)$ are linearly dependent. Thus, the instantaneous angular frequency with slope $K_{\rm FM}$ of the modulator characteristic is given as follows:
- $$\omega_{\rm A}(t) = \omega_{\rm T} + K_{\rm FM} \cdot q(t) \hspace{0.05cm}.$$
- The push-pull circuit consisting of both capacitance diodes is used, among other things, to compensate for imbalances and thus reduce quadratic distortion.
- With an input of $A_0+{\rm d}q(t)/{\rm d}t$ , the frequency-modulated signal $s(t)$ is obtained at the output.
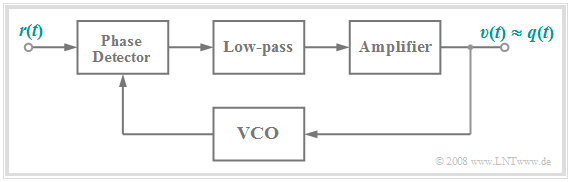
PLL Realization of FM demodulator
The following diagram shows a second possible realization of an FM demodulator. A detailed circuit description of the PLL FM demodulator and further demodulators – for example, using an edge discriminator – can be found in [Mäu 88][1].
In short, this circuit, which operates as a $($Phase–Locked–Loop, $\rm PLL)$ , can be described as follows:
- The phase detector determines the phase differences (distances of zero intercepts) between the received signal $r(t)$ and the comparison signal provided by the VCO.
- After low-pass filtering and amplification, the output signal $v(t)$ is approximately equal to the source signal $q(t)$ if it has been FM-modulated at the transmit end.
- The output signal $v(t)$ is simultaneously applied to the input of the Voltage Controlled Oscillator,, abbreviated as $\rm VCO$.
- The output signal of the VCO is permanently readjusted in such a way that its frequency corresponds as closely to the instantaneous frequency $f_{\rm A}(t)$ of the received signal $r(t)$ .
Aufgaben zum Kapitel
Aufgabe 3.5: PM und FM bei Rechtecksignalen
Aufgabe 3.5Z: Phasenmodulation eines Trapezsignals
Aufgabe 3.6: PM oder FM? Oder AM?
Aufgabe 3.7: Winkelmodulation einer harmonischen Schwingung
Aufgabe 3.8: Modulationsindex und Bandbreite
Aufgabe 3.9: Kreisbogen und Parabel
Quellenverzeichnis