Difference between revisions of "Channel Coding/Soft-in Soft-Out Decoder"
| Line 82: | Line 82: | ||
*would be close to zero for $\text{channel 3}$ and $\text{channel 4}$ .<br> | *would be close to zero for $\text{channel 3}$ and $\text{channel 4}$ .<br> | ||
| − | == | + | == Reliability information - Log Likelihood Ratio== |
<br> | <br> | ||
| − | + | Let $x ∈ \{+1, \, -1\}$ be a binary random variable with probabilities ${\rm Pr}(x = +1)$ and ${\rm Pr}(x = \, -1)$. For coding theory, it proves convenient in terms of computation times to use the natural logarithm of the quotient instead of the probabilities ${\rm Pr}(x = ±1)$ .<br> | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ The <b>log likelihood ratio (LLR)</b> of the random variable $x ∈ \{+1, \, -1\}$ is: |
::<math>L(x)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(x = +1)}{ {\rm Pr}(x = -1)}\hspace{0.05cm}.</math> | ::<math>L(x)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(x = +1)}{ {\rm Pr}(x = -1)}\hspace{0.05cm}.</math> | ||
| − | + | For unipolar/symbolic representation $(+1 → 0$ and $-1 → 1)$ applies accordingly with $\xi ∈ \{0, \, 1\}$: | |
::<math>L(\xi)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(\xi = 0)}{ {\rm Pr}(\xi = 1)}\hspace{0.05cm}.</math>}}<br> | ::<math>L(\xi)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(\xi = 0)}{ {\rm Pr}(\xi = 1)}\hspace{0.05cm}.</math>}}<br> | ||
| − | + | Below is given the nonlinear relationship between ${\rm Pr}(x = ±1)$ and $L(x)$ . Replacing ${\rm Pr}(x = +1)$ with ${\rm Pr}(\xi = 0)$, the middle row gives the $L$–value of the unipolar random variable $\xi$.<br> | |
| − | [[File:P ID2975 KC T 4 1 S2a v1.png|center|frame| | + | [[File:P ID2975 KC T 4 1 S2a v1.png|center|frame|Probability and LLR|class=fit]] |
| − | + | You can see: | |
| − | * | + | *The more likely random value of $x ∈ \{+1, \, -1\}$ is given by the <b>sign</b> ⇒ ${\rm sign} \ L(x)$ given.<br> |
| − | * | + | *In contrast, the <b>absolute value</b> ⇒ $|L(x)|$ indicates the reliability for the result ${\rm sign}(L(x))$ .<br><br> |
| − | [[File:P ID2976 KC T 4 1 S2b v2.png|right|frame| | + | [[File:P ID2976 KC T 4 1 S2b v2.png|right|frame|BSC model]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ We consider the outlined [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC| "BSC model"]] with bipolar representation. Here, with the corruption probability $\varepsilon = 0.1$ and the two random variables $x ∈ \{+1, \, -1\}$ and $y ∈ \{+1, \, -1\}$ at the input and output of the channel: |
::<math>L(y\hspace{0.05cm}\vert\hspace{0.05cm}x) = | ::<math>L(y\hspace{0.05cm}\vert\hspace{0.05cm}x) = | ||
| Line 114: | Line 114: | ||
\\ {\rm f\ddot{u}r} \hspace{0.15cm} y = -1. \\ \end{array}</math> | \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = -1. \\ \end{array}</math> | ||
| − | + | For example, $\varepsilon = 0.1$ results in the following numerical values (compare upper table): | |
::<math>L(y = +1\hspace{0.05cm}\vert\hspace{0.05cm}x) = | ::<math>L(y = +1\hspace{0.05cm}\vert\hspace{0.05cm}x) = | ||
| Line 120: | Line 120: | ||
L(y = -1\hspace{0.05cm}\vert\hspace{0.05cm}x) = -2.197\hspace{0.05cm}.</math> | L(y = -1\hspace{0.05cm}\vert\hspace{0.05cm}x) = -2.197\hspace{0.05cm}.</math> | ||
| − | + | This example shows that the so-called LLR algebra can also be applied to conditional probabilities. <br>In the [[Aufgaben:Exercise_4.1Z:_Log_Likelihood_Ratio_at_the_BEC_Model|"Exercise 4.1Z"]] the BEC–model is described in a similar way.}}<br> | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ |
| − | In | + | In another example, now consider the [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_Binary_Input|"AWGN channel"]] with the conditional probability density functions |
| − | [[File:P ID2977 KC T 4 1 S2c v3.png|right|frame| | + | [[File:P ID2977 KC T 4 1 S2c v3.png|right|frame|Conditional AWGN density functions|class=fit]] |
::<math>f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 )\hspace{-0.1cm} = \hspace{-0.1cm} | ::<math>f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 )\hspace{-0.1cm} = \hspace{-0.1cm} | ||
| Line 132: | Line 132: | ||
\frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y+1)^2}/(2\sigma^2) } \hspace{0.05cm}.</math> | \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y+1)^2}/(2\sigma^2) } \hspace{0.05cm}.</math> | ||
| − | In | + | In the graphic, two exemplary Gaussian functions are shown as blue and red curves, respectively.<br> |
<br clear=all> | <br clear=all> | ||
| − | + | The total PDF of the output signal $y$ is obtained from the (equally) weighted sum: | |
::<math>f_{y } \hspace{0.05cm} (y ) = 1/2 \cdot \big [ f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 ) \hspace{0.1cm} + \hspace{0.1cm} | ::<math>f_{y } \hspace{0.05cm} (y ) = 1/2 \cdot \big [ f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 ) \hspace{0.1cm} + \hspace{0.1cm} | ||
| Line 141: | Line 141: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | We now calculate the probability that the received value $y$ lies in a (very) narrow interval of width $\Delta$ around $y_0 = 0.25$ . One obtains approximately | |
::<math>{\rm Pr} (\vert y - y_0\vert \le{\it \Delta}/2 \hspace{0.05cm} | ::<math>{\rm Pr} (\vert y - y_0\vert \le{\it \Delta}/2 \hspace{0.05cm} | ||
| Line 150: | Line 150: | ||
\frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2) } \hspace{0.05cm}.</math> | \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2) } \hspace{0.05cm}.</math> | ||
| − | + | The slightly larger vertical lines denote the conditions, the smaller ones the absolute value.<br> | |
| − | + | The LLR of the conditional probability in the forward direction $($meaning: output $y$ for a given input $x)$ is thus obtained as the logarithm of the quotient of both expressions: | |
::<math>L(y = y_0\hspace{0.05cm}\vert\hspace{0.05cm}x) = | ::<math>L(y = y_0\hspace{0.05cm}\vert\hspace{0.05cm}x) = | ||
| Line 158: | Line 158: | ||
{\rm ln} \left [ {\rm e} ^{ - [ {(y_0-1)^2}+{(y_0+1)^2}]/(2\sigma^2)} \right ] = \frac{(y_0+1)^2-(y_0-1)^2}{2\cdot \sigma^2} = \frac{2 \cdot y_0}{\sigma^2}\hspace{0.05cm}. </math> | {\rm ln} \left [ {\rm e} ^{ - [ {(y_0-1)^2}+{(y_0+1)^2}]/(2\sigma^2)} \right ] = \frac{(y_0+1)^2-(y_0-1)^2}{2\cdot \sigma^2} = \frac{2 \cdot y_0}{\sigma^2}\hspace{0.05cm}. </math> | ||
| − | + | If we now replace the auxiliary $y_0$ with the (general) random $y$ at the AWGN output, the final result is: | |
::<math>L(y \hspace{0.05cm}\vert\hspace{0.05cm}x) = {2 \cdot y}/{\sigma^2} =K_{\rm L} \cdot y\hspace{0.05cm}. </math> | ::<math>L(y \hspace{0.05cm}\vert\hspace{0.05cm}x) = {2 \cdot y}/{\sigma^2} =K_{\rm L} \cdot y\hspace{0.05cm}. </math> | ||
| − | + | Here $K_{\rm L} = 2/\sigma^2$ is a constant that depends solely on the standard deviation of the Gaussian }}.<br> | |
| − | == | + | == Symbol-wise soft in soft out decoding == |
<br> | <br> | ||
Wir gehen nun von einem $(n, \ k)$–Blockcode aus, wobei das Codewort $\underline{x} = (x_1, \ \text{...} \ , \ x_n)$ durch den Kanal in das Empfangswort $\underline{y} = (y_1, \ \text{...} \ , \ y_n)$ verfälscht wird. | Wir gehen nun von einem $(n, \ k)$–Blockcode aus, wobei das Codewort $\underline{x} = (x_1, \ \text{...} \ , \ x_n)$ durch den Kanal in das Empfangswort $\underline{y} = (y_1, \ \text{...} \ , \ y_n)$ verfälscht wird. | ||
| Line 326: | Line 326: | ||
* Der gesuchte extrinsische $L$–Wert $L_{\rm E}(3)$ ergibt sich aus den Metriken $\alpha_2$ (in Vorwärtsrichtung) und $\beta_3$ (in Rückwärtsrichtung) sowie der Apriori–Information $\gamma_3$ über das Symbol $i = 3$.<br> | * Der gesuchte extrinsische $L$–Wert $L_{\rm E}(3)$ ergibt sich aus den Metriken $\alpha_2$ (in Vorwärtsrichtung) und $\beta_3$ (in Rückwärtsrichtung) sowie der Apriori–Information $\gamma_3$ über das Symbol $i = 3$.<br> | ||
| − | == | + | == Basic structure of concatenated coding systems == |
<br> | <br> | ||
Die wichtigsten Kommunikationssysteme der letzten Jahre verwenden zwei unterschiedliche Kanalcodes. Man spricht dann von '''verketteten Codiersystemen''' (englisch: <i>Concatenated Codes</i>). Auch bei relativ kurzen Komponentencodes $\mathcal{C}_1$ und $\mathcal{C}_2$ ergibt sich für den verketteten Code $\mathcal{C}$ eine hinreichend große Codewortlänge $n$, die ja bekanntlich erforderlich ist, um sich der Kanalkapazität anzunähern.<br> | Die wichtigsten Kommunikationssysteme der letzten Jahre verwenden zwei unterschiedliche Kanalcodes. Man spricht dann von '''verketteten Codiersystemen''' (englisch: <i>Concatenated Codes</i>). Auch bei relativ kurzen Komponentencodes $\mathcal{C}_1$ und $\mathcal{C}_2$ ergibt sich für den verketteten Code $\mathcal{C}$ eine hinreichend große Codewortlänge $n$, die ja bekanntlich erforderlich ist, um sich der Kanalkapazität anzunähern.<br> | ||
Revision as of 20:50, 22 October 2022
Contents
- 1 # OVERVIEW OF THE FOURTH MAIN CHAPTER #
- 2 Hard Decision vs. Soft Decision
- 3 Reliability information - Log Likelihood Ratio
- 4 Symbol-wise soft in soft out decoding
- 5 Zur Berechnung der extrinsischen L–Werte
- 6 BCJR–Decodierung: Vorwärts–Rückwärts–Algorithmus
- 7 Basic structure of concatenated coding systems
- 8 Aufgaben zum Kapitel
- 9 Quellenverzeichnis
# OVERVIEW OF THE FOURTH MAIN CHAPTER #
The last main chapter of the channel coding book describes iterative decoding techniques as used in most of today's (2017) communication systems. This is due to the following reasons:
- To approach the channel capacity, one needs very long codes.
- But for long codes, blockwise maximum likelihood decoding is almost impossible.
The decoder complexity can be significantly reduced with almost the same quality if two (or more) short channel codes are linked together and the newly acquired (soft) information is exchanged between the decoders at the receiver in several steps - i.e. iteratively.
The breakthrough in the field came in the early 1990s with the invention of turbo codes by "Claude Berrou" and shortly thereafter with the rediscovery of low-density parity-check codes by wikipedia.org/wiki/David_J._C._MacKay "David J. C. MacKay" and "Radford M. Neal", after the LDPC codes developed as early as 1961 by "Robert G. Gallager" had been forgotten in the meantime.
Specifically, the fourth main chapter discusses:
- a comparison of Hard Decision and Soft Decision,
- the quantification of reliability information by log likelihood ratios (LLR),
- the principle of symbol-wise soft in soft out (SISO) decoding,
- the definition of apriori L value, a posteriori L-value and extrinsic L value,
- the basic structure of serially concatenated and parallel concatenated coding systems, respectively,
- the characteristics of product codes and their hard decision decoding,
- the basic structure, decoding algorithm and performance of turbo codes,
- basic information on the low-density parity-check codes and their applications.
Hard Decision vs. Soft Decision
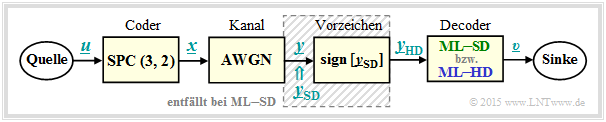
To introduce the topic discussed here, let us consider the following message transmission system with coding.
In the following, all symbols are given in bipolar representation: "$0$" → "$+1$" and "$1$" → "$-1$".
- The symbol sequence $\underline{u} = (u_1, \ u_2)$ is assigned to the code sequence $\underline{x} = (x_1, \ x_2, \ x_3) = (u_1, \ u_2, \ p)$ where for the parity bit $p = u_1 ⊕ u_2$ holds ⇒ "Single Parity–check Code" ⇒ ${\rm SPC} (3, 2, 2)$.
- The "AWGN–channel" changes the binary symbols $x_i ∈ \{+1, \ –1\}$ to real-valued output values $y_i$, for example according to $\text{channel 4}$ the table below: $x_1 = +1$ ⇒ $y_1 = +0. 9$, $x_2 = \, -1$ ⇒ $y_2 = +0.1$ and $x_3 = \, -1$ ⇒ $y_3 = +0.1$.
- Decoding is done according to the criterion "Maximum-Likelihood" $\text{(blockwise ML)}$, distinguishing between hard decision $\rm {(ML–HD)}$ and soft decision $\rm {(ML–SD)}$ .
- The whole block diagram corresponds to $\rm ML–HD$. Here, only the signs of the AWGN output values ⇒ $y_{\rm HD, \ \it i} = {\rm sign}\big [y_{\rm SD, \ \it i}\big ]$ are evaluated for decoding. In soft decision $\rm {(ML–SD)}$ one omits the shaded block and directly evaluates the continuous value input variables $y_{\rm SD, \ \it i}$ .
For all columns of this table it is assumed:
- the message block $\underline{u} = (0, 1)$, bipolar representable as $(+1, \, –1)$,
- the ${\rm SPC} \ (3, 2)$–coded block $\underline{x} = (0, 1, 1)$ respectively in bipolar representation $(+1, \, -1, \, -1)$.
Thus, the four columns differ only by different AWGN realizations.
$\text{Definition:}$ From the example table you can see:
- $\text{Hard Decision:}$ The symbol sequence $\underline{v}_{\rm HD}$ results from the hard decided channel values $\underline{y}_{\rm HD}$ (blue background).
In our example, only the constellations according to $\text{channel 1}$ and $\text{channel 2}$ are decoded without errors.
- $\text{Soft Decision:}$ The symbol sequence $\underline{v}_{\rm SD}$ results from the "soft" channel output values $\underline{y}_{\rm SD}$ (green background).
Now, in this example, it is also correctly decided at $\text{channel 3}$
The entries in the example table above are to be interpreted as follows:
- For ideal channel ⇒ $\text{channel 1}$ ⇒ $\underline{x} = \underline{y}_{\rm SD} = \underline{y}_{\rm HD}$ there is no difference between the (blue) conventional hard decision variant $\rm {(ML–HD)}$ and the (green) soft decision variant $\rm {(ML–SD)}$.
- Setting according $\text{channel 2}$ demonstrates low signal distortions. Because of $\underline{y}_{\rm HD} = \underline{x}$ (which means that the channel does not distort the signs) also $\rm ML–HD$ gives the correct result $\underline{v}_{\rm HD} = \underline{u}$.
- For $\text{channel 3}$ there is $\underline{y}_{\rm HD} ≠ \underline{x}$ and there is also no ${\rm SPC} \ (3, 2)$–assignment $\underline{u}$ ⇒ $\underline{y}_{\rm HD}$. The ML–decoder reports here by outputting $\underline{v}_{\rm HD} = \rm (E, \ E)$ that it failed in decoding this block. "$\rm E$" stands for "Erasure" .
- Also the soft decision decoder recognizes that decoding based on the signs does not work. Based on the $\underline{y}_{\rm SD}$–values, however, it recognizes that with high probability the second bit has been corrupted and decides to use the correct symbol sequence $\underline{v}_{\rm SD} = (+1, \, -1) = \underline{u}$.
- In $\text{channel 4}$ both the signs of bit 2 and bit 3 are changed by the AWGN–channel, leading to the result $\underline{v}_{\rm HD} = (+1, +1) ≠ \underline{u}(+1, \, -1)$ ⇒ a block error and a bit error at the same time. Also the soft decision decoder gives the same wrong result here.
The decoding variant "ML–SD" also offers the advantage over "ML–HD" that it is relatively easy to assign a reliability value to each decoding result (in the above table, however, this is not specified). This reliability value
- would have its maximum value at $\text{channel 1}$ ,
- would be significantly smaller for $\text{channel 2}$ ,
- would be close to zero for $\text{channel 3}$ and $\text{channel 4}$ .
Reliability information - Log Likelihood Ratio
Let $x ∈ \{+1, \, -1\}$ be a binary random variable with probabilities ${\rm Pr}(x = +1)$ and ${\rm Pr}(x = \, -1)$. For coding theory, it proves convenient in terms of computation times to use the natural logarithm of the quotient instead of the probabilities ${\rm Pr}(x = ±1)$ .
$\text{Definition:}$ The log likelihood ratio (LLR) of the random variable $x ∈ \{+1, \, -1\}$ is:
- \[L(x)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(x = +1)}{ {\rm Pr}(x = -1)}\hspace{0.05cm}.\]
For unipolar/symbolic representation $(+1 → 0$ and $-1 → 1)$ applies accordingly with $\xi ∈ \{0, \, 1\}$:
- \[L(\xi)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(\xi = 0)}{ {\rm Pr}(\xi = 1)}\hspace{0.05cm}.\]
Below is given the nonlinear relationship between ${\rm Pr}(x = ±1)$ and $L(x)$ . Replacing ${\rm Pr}(x = +1)$ with ${\rm Pr}(\xi = 0)$, the middle row gives the $L$–value of the unipolar random variable $\xi$.
You can see:
- The more likely random value of $x ∈ \{+1, \, -1\}$ is given by the sign ⇒ ${\rm sign} \ L(x)$ given.
- In contrast, the absolute value ⇒ $|L(x)|$ indicates the reliability for the result ${\rm sign}(L(x))$ .
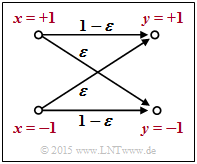
$\text{Example 1:}$ We consider the outlined "BSC model" with bipolar representation. Here, with the corruption probability $\varepsilon = 0.1$ and the two random variables $x ∈ \{+1, \, -1\}$ and $y ∈ \{+1, \, -1\}$ at the input and output of the channel:
- \[L(y\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(y\hspace{0.05cm}\vert\hspace{0.05cm}x = +1) }{ {\rm Pr}(y\hspace{0.05cm}\vert\hspace{0.05cm}x = -1)} = \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} \big[(1 - \varepsilon)/\varepsilon \big]\\ {\rm ln} \hspace{0.15cm}\big [\varepsilon/(1 - \varepsilon)\big] \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm} y = +1, \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = -1. \\ \end{array}\]
For example, $\varepsilon = 0.1$ results in the following numerical values (compare upper table):
- \[L(y = +1\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{0.9}{0.1} = +2.197\hspace{0.05cm}, \hspace{0.8cm} L(y = -1\hspace{0.05cm}\vert\hspace{0.05cm}x) = -2.197\hspace{0.05cm}.\]
This example shows that the so-called LLR algebra can also be applied to conditional probabilities.
In the "Exercise 4.1Z" the BEC–model is described in a similar way.
$\text{Example 2:}$ In another example, now consider the "AWGN channel" with the conditional probability density functions
- \[f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y-1)^2}/(2\sigma^2) } \hspace{0.05cm},\]
- \[f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=-1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y+1)^2}/(2\sigma^2) } \hspace{0.05cm}.\]
In the graphic, two exemplary Gaussian functions are shown as blue and red curves, respectively.
The total PDF of the output signal $y$ is obtained from the (equally) weighted sum:
- \[f_{y } \hspace{0.05cm} (y ) = 1/2 \cdot \big [ f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 ) \hspace{0.1cm} + \hspace{0.1cm} f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert \hspace{0.05cm}x=-1 ) \big ] \hspace{0.05cm}.\]
We now calculate the probability that the received value $y$ lies in a (very) narrow interval of width $\Delta$ around $y_0 = 0.25$ . One obtains approximately
- \[{\rm Pr} (\vert y - y_0\vert \le{\it \Delta}/2 \hspace{0.05cm} \Big \vert \hspace{0.05cm}x=+1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2) } \hspace{0.05cm},\]
- \[{\rm Pr} (\vert y - y_0\vert \le {\it \Delta}/2 \hspace{0.05cm} \Big \vert \hspace{0.05cm}x=-1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2) } \hspace{0.05cm}.\]
The slightly larger vertical lines denote the conditions, the smaller ones the absolute value.
The LLR of the conditional probability in the forward direction $($meaning: output $y$ for a given input $x)$ is thus obtained as the logarithm of the quotient of both expressions:
- \[L(y = y_0\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \left [ \frac{{\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2)}}{{\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2)}} \right ] = {\rm ln} \left [ {\rm e} ^{ - [ {(y_0-1)^2}+{(y_0+1)^2}]/(2\sigma^2)} \right ] = \frac{(y_0+1)^2-(y_0-1)^2}{2\cdot \sigma^2} = \frac{2 \cdot y_0}{\sigma^2}\hspace{0.05cm}. \]
If we now replace the auxiliary $y_0$ with the (general) random $y$ at the AWGN output, the final result is:
- \[L(y \hspace{0.05cm}\vert\hspace{0.05cm}x) = {2 \cdot y}/{\sigma^2} =K_{\rm L} \cdot y\hspace{0.05cm}. \]
Here $K_{\rm L} = 2/\sigma^2$ is a constant that depends solely on the standard deviation of the Gaussian
.
Symbol-wise soft in soft out decoding
Wir gehen nun von einem $(n, \ k)$–Blockcode aus, wobei das Codewort $\underline{x} = (x_1, \ \text{...} \ , \ x_n)$ durch den Kanal in das Empfangswort $\underline{y} = (y_1, \ \text{...} \ , \ y_n)$ verfälscht wird.
- Bei langen Codes ist eine Maximum–a–posteriori–Entscheidung auf Blockebene – kurz: $\text{ block–wise MAP}$ – sehr aufwändig.
- Man müsste unter den $2^k $ zulässigen Codeworten $\underline{x}_j ∈ \mathcal{C}$ dasjenige mit der größten Rückschlusswahrscheinlichkeit (englisch: A Posteriori Probability, APP) finden.
- Das auszugebende Codewort $\underline{z}$ wäre in diesem Fall $\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}j} \hspace{0.03cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}j} |\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.$
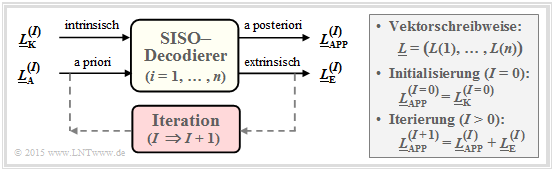
Eine zweite Möglichkeit ist die Decodierung auf Bitebene. Der dargestellte symbolweise (oder bitweise) $\text{Soft–in Soft–out Decoder}$ hat die Aufgabe, alle Codewortbits $x_i ∈ \{0, \, 1\}$ entsprechend maximaler Rückschlusswahrscheinlichkeit ${\rm Pr}(x_i | \underline{y})$ zu decodieren. Mit der Laufvariablen $i = 1, \text{...} , \ n$ gilt dabei:
- Der entsprechende $L$–Wert (englisch: Log Likelihood Ratio, LLR) für das $i$–te Codebit lautet:
- \[L_{\rm APP} (i) = L(x_i\hspace{0.05cm}|\hspace{0.05cm}\underline{y}) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x_i = 0\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}{{\rm Pr}(x_i = 1\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}\hspace{0.05cm} . \]
- Der Decoder arbeitet iterativ. Bei der Initialisierung $($in der Grafik gekennzeichnet durch den Parameter $I = 0)$ ist $L_{\rm APP}(i) = L_{\rm K}(i)$, wobei das Kanal–LLR $L_{\rm K}(i)$ durch den Empfangswert $y_i$ gegeben ist.
- Berechnet wird zudem der extrinsische $L$–Wert $L_{\rm E}(i)$, der die gesamte Information quantifiziert, die alle anderen Bits $(j ≠ i)$ aufgrund der Code–Eigenschaften über das betrachtete $i$–te Bit liefern.
- Bei der nächsten Iteration $($ab $I = 1)$ wird $L_{\rm E}(i)$ bei der Berechnung von $L_{\rm APP}(i)$ als Apriori–Information $L_{\rm A}(i)$ berücksichtigt. Für das neue Aposteriori–LLR in der Iteration $I + 1$ gilt somit:
- \[L_{\hspace{0.1cm}\rm APP}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm A}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm E}^{(I)} (i)\hspace{0.05cm} . \]
- Die Iterationen werden fortgesetzt, bis alle Beträge $|L_{\rm APP}(i)|$ größer sind als ein vorzugebender Wert. Das wahrscheinlichste Codewort $\underline{z}$ ergibt sich dann aus den Vorzeichen aller $L_{\rm APP}(i)$, mit $i = 1, \ \text{...} , \ n$.
- Bei einem systematischen Code geben die ersten $k$ Bit von $\underline{z}$ das gesuchte Informationswort an, das mit großer Wahrscheinlichkeit mit der gesendeten Nachricht $\underline{u}$ übereinstimmen wird.
Diese Beschreibung des SISO–Decodierers nach [Bos98][1] soll an dieser Stelle in erster Linie die unterschiedlichen $L$–Werte verdeutlichen. Das große Potential der symbolweisen Decodierung erkennt man erst im Zusammenhang mit verketteten Codiersystemen.
Zur Berechnung der extrinsischen L–Werte
Die Schwierigkeit bei der symbolweisen iterativen Decodierung ist im allgemeinen die Bereitstellung der extrinsischen $L$–Werte $L_{\rm E}(i)$. Bei einem Code der Länge $n$ gilt hierbei für die Laufvariable: $i = 1, \ \text{...} , \ n$.
$\text{Definition:}$ Der extrinsische $L$–Wert (englisch: extrinsic LLR ) ist ein Maß für die Informationen, den die anderen Symbole $(j ≠ i)$ des Codewortes über das $i$–te Codesymbol liefern, ausgedrückt als Log–Likelihood–Verhältnis. Wir benennen diesen Kennwert mit $L_{\rm E}(i)$.
Wir berechnen nun die extrinsischen $L$–Werte $L_{\rm E}(i)$ für zwei beispielhafte Codes.
$\text{Repetition Code}$ ⇒ ${\rm RC} \ (n, 1, n)$
Ein Wiederholungscode zeichnet sich dadurch aus, dass alle $n$ Codesymbole $x_i ∈ \{0, \, 1\}$ identisch sind. Der extrinsische $L$–Wert für das $i$–ten Symbol ist hier sehr einfach anzugeben und lautet:
- \[L_{\rm E}(i) = \hspace{0.05cm}\sum_{j \ne i} \hspace{0.1cm} L_j \hspace{0.3cm}{\rm mit}\hspace{0.3cm}L_j = L_{\rm APP}(j) \hspace{0.05cm}.\]
- Ist die Summe über alle $L_{j ≠ i}$ positiv, so bedeutet dies aus Sicht der anderen $L$–Werte eine Präferenz für die Entscheidung $x_i = 0$.
- Bei negativer Summe ist dagegen $x_i = 1$ wahrscheinlicher.
- $L_{\rm E}(i) = 0$ erlaubt keine Vorhersage.
$\text{Beispiel 5:}$ Wir betrachten die Decodierung des Wiederholungscodes $\text{RC (4, 1,4)}$. Wir gehen dabei von drei verschiedene Annnahmen für das Log Likelihood Ratio $\underline{L}_{\rm A}^{(I=0)} = \underline{L}_{\rm APP}$ aus.
$\text{Decodierbeispiel (A):}$
- $$\underline{L}_{\rm APP} = (+1, -1, +3, -1)\text{:}$$
- $$L_{\rm E}(1) = -1+3-1 = +1\hspace{0.05cm},$$
- $$L_{\rm E}(2) = +1+3-1 = +3\hspace{0.05cm},$$
- $$L_{\rm E}(3) = +1-1 -1= -1\hspace{0.05cm},$$
- $$L_{\rm E}(4) = +1-1 +3 = +3\hspace{0.05cm}$$
- $$\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm E}^{(I=0)}= (+1, +3, -1, +3) \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm A}^{(I=1)}=\underline{L}_{\rm A}^{(I=0)}+ \underline{L}_{\rm E}^{(I=0)}= (+2, +2, +2, +2)$$
- Zu Beginn $(I=0)$ weisen die positiven $L_{\rm E}$–Werte auf $x_1 = 0$, $x_2 = 0$ und $x_4 = 0$ hin, während $x_3 =1$ wahrscheinlicher ist.
- Bereits nach einer Iteration $(I=1)$ sind alle $L_{\rm A}$–Werte positiv ⇒ Informationsbit wird als $u = 0$ decodiert.
- Weitere Iterationen bringen nichts.
$\text{Decodierbeispiel (B):}$ $$\underline{L}_{\rm APP} = (+1, +1, -4, +1)\text{:}$$ $$\underline{L}_{\rm E}^{(I=0)} = \ (-2, -2, +3, -2)$$
- Obwohl zu Beginn drei Vorzeichen falsch waren, sind nach zwei Iterationen alle $L_{\rm A}$–Werte negativ.
- Das Informationsbit wird als $u = 1$ decodiert.
$\text{Decodierbeispiel (C):}$ $$\underline{L}_{\rm APP} = (+1, +1, -3, +1)\text{:}$$ $$\underline{L}_{\rm E}^{(I=0)} = (-1, -1, +3, -1)$$
- Alle $L_{\rm A}$–Werte sind schon nach einer Iteration Null.
- Das Informationsbit kann nicht decodiert werden, obwohl die Ausgangslage nicht viel schlechter war als bei $\rm (B)$.
- Weitere Iterationen bringen auch hier nichts.
$\text{Single Parity–check Code}$ ⇒ ${\rm SPC} \ (n, \ n \, -1, \ 2)$
Bei jedem Single Parity–check Code ist die Anzahl der Einsen in jedem Codewort geradzahlig. Oder anders ausgedrückt: Für jedes Codewort $\underline{x}$ ist das Hamming–Gewicht $w_{\rm H}(\underline{x})$ geradzahlig.
$\text{Definition:}$ Das Codewort $\underline{x}^{(–i)}$ beinhalte alle Symbole mit Ausnahme von $x_i$ ⇒ Vektor der Länge $n -1$. Damit lautet der $\text{extrinsische }L\text{–Wert}$ bezüglich des $i$–ten Symbols, wenn $\underline{x}$ empfangen wurde:
- \[L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} \vert\hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} \vert \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.\]
Wie in der Aufgabe 4.4 gezeigt werden soll, kann hierfür auch geschrieben werden:
- \[L_{\rm E}(i) = 2 \cdot {\rm tanh}^{-1} \hspace{0.1cm} \left [ \prod\limits_{j \ne i}^{n} \hspace{0.15cm}{\rm tanh}(L_j/2) \right ] \hspace{0.3cm}{\rm mit}\hspace{0.3cm}L_j = L_{\rm APP}(j) \hspace{0.05cm}.\]
$\text{Beispiel 6:}$ Wir gehen vom Single Parity–check Code mit $n = 3, \ k = 2$ ⇒ kurz ${\rm SPC} \ (3, \ 2, \ 2)$ aus.
Die $2^k = 4$ gültigen Codeworte $\underline{x} = \{x_1, x_2, x_3\}$ lauten bei bipolarer Beschreibung ⇒ $x_i ∈ \{±1\}$:
- $$ \underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{-0.05cm}, $$
- $$\underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, $$
- $$\underline{x}_2 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} +1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, $$
- $$\underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} +1)\hspace{-0.05cm}. $$
Bei diesem Code ist also das Produkt $x_1 \cdot x_2 \cdot x_3$ stets positiv.
Die obige Tabelle zeigt den Decodiervorgang für $\underline{L}_{\rm APP} = (+2.0, +0.4, \, –1.6)$. Die harte Entscheidung nach den Vorzeichen von $L_{\rm APP}(i)$ ergäbe hier $(+1, +1, \, -1)$, also kein gültiges Codewort des ${\rm SP}(3, \ 2, \ 2)$.
Rechts in der Tabelle sind die dazugehörigen extrinsischen $L$–Werte eingetragen:
- \[L_{\rm E}(1) = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (0.2) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.131\hspace{0.05cm}, \]
- \[L_{\rm E}(2) =2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.518\hspace{0.05cm}, \]
- \[L_{\rm E}(3) =2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (0.2)\hspace{0.05cm}\right ] = +0.151\hspace{0.05cm}.\]
Die zweite Gleichung lässt sich wie folgt interpretieren:
- $L_{\rm APP}(1) = +2.0$ und $L_{\rm APP}(3) = \, -1.6$ sagen aus, dass das erste Bit eher $+1$ als $-1$ ist und das dritte Bit eher $-1$ als $+1$. Die Zuverlässigkeit (der Betrag) ist beim ersten Bit etwas größer als beim dritten.
- Die extrinsische Information $L_{\rm E}(2) = \, -0.518$ berücksichtigt nur die Informationen von Bit 1 und Bit 3 über Bit 2. Aus deren Sicht ist das zweite Bit eine $-1$ mit der Zuverlässigkeit $0.518$.
- Der vom Empfangswert $y_2$ abgeleitete $L$–Wert ⇒ $L_{\rm APP}(2) = +0.4$ hat für das zweite Bit eine $+1$ vermuten lassen. Die Diskrepanz wird hier bereits in der Iteration $I = 1$ aufgelöst.
- Entschieden wird hier für das Codewort $\underline{x}_1$. Bei $0.518 < L_{\rm APP}(2) < 1.6$ würde das Ergebnis $\underline{x}_1$ erst nach mehreren Iterationen vorliegen. Für $L_{\rm APP}(2) > 1.6$ liefert der Decoder dagegen $\underline{x}_0$.
BCJR–Decodierung: Vorwärts–Rückwärts–Algorithmus
Ein Beispiel für die iterative Decodierung von Faltungscodes ist der BCJR–Algorithmus, benannt nach dessen Erfindern L. R. Bahl, J. Cocke, F. Jelinek und J. Raviv ⇒ [BCJR74][2]. Der Algorithmus weist viele Parallelen zur sieben Jahren älteren Viterbi–Decodierung auf, doch auch einige signifikante Unterschiede:
- Während Viterbi die Gesamtsequenz schätzt ⇒ $\text{block–wise Maximum Likelihood}$, minimiert der BCJR–Algorithmus die Bitfehlerwahrscheinlichkeit ⇒ $\text{ bit–wise MAP}$.
- Der Viterbi–Algorithmus kann (in seiner ursprünglichen Form) keine Softinformation verarbeiten. Dagegen gibt der BCJR–Algorithmus bei jeder Iteration für jedes einzelne Symbol (Bit) einen Zuverlässigkeitswert an, der bei späteren Iterationen berücksichtigt wird.
Die Abbildung soll – fast unzulässig vereinfacht – die unterschiedliche Vorgehensweise von Viterbi–Algorithmus (links) und BCJR–Algorithmus (rechts) verdeutlichen. Zugrunde liegt ein Faltungscode mit dem Gedächtnis $m = 1$ und der Länge $L = 4$ ⇒ Gesamtlänge (mit Terminierung) $L' = 5$.
- Der Viterbi–Algorithmus sucht und findet den wahrscheinlichsten Pfad von ${\it \Gamma}_0(S_0)$ nach ${\it \Gamma}_5(S_0)$, nämlich $S_0 → S_1 → S_0 → S_0 → S_1→ S_0 $. Wir verweisen auf die Musterlösung zur Aufgabe 3.9Z.
Die Skizze für den BCJR–Algorithmus verdeutlicht die Gewinnung des extrinsischen $L$–Wertes für das dritte Symbol ⇒ $L_{\rm E}(3)$. Der relevante Bereich im Trellis ist schraffiert:
- Bei der Abarbeitung des Trellisdiagramms in Vorwärtsrichtung gewinnt man – in gleicher Weise wie bei Viterbi – die Metriken $\alpha_1, \ \alpha_2, \ \text{...}\hspace{0.05cm} , \ \alpha_5$. Zur Berechnung von $L_{\rm E}(3)$ benötigt man hiervon $\alpha_2$.
- Anschließend durchläuft man das Trellisdiagramm rückwärts (also von rechts nach links) und erhält damit die Metriken $\beta_4, \ \beta_3, \ \text{...}\hspace{0.05cm} , \ \beta_0$ entsprechend der unteren Skizze.
- Der gesuchte extrinsische $L$–Wert $L_{\rm E}(3)$ ergibt sich aus den Metriken $\alpha_2$ (in Vorwärtsrichtung) und $\beta_3$ (in Rückwärtsrichtung) sowie der Apriori–Information $\gamma_3$ über das Symbol $i = 3$.
Basic structure of concatenated coding systems
Die wichtigsten Kommunikationssysteme der letzten Jahre verwenden zwei unterschiedliche Kanalcodes. Man spricht dann von verketteten Codiersystemen (englisch: Concatenated Codes). Auch bei relativ kurzen Komponentencodes $\mathcal{C}_1$ und $\mathcal{C}_2$ ergibt sich für den verketteten Code $\mathcal{C}$ eine hinreichend große Codewortlänge $n$, die ja bekanntlich erforderlich ist, um sich der Kanalkapazität anzunähern.
Zunächst seien einige Beispiele aus dem Mobilfunk genannt:
- Bei GSM (Global System for Mobile Communications, zweite Mobilfunkgeneration) wird zunächst die Datenbitrate von $9.6 \ \rm kbit/s$ auf $12 \ \rm kbit/s$ erhöht, um auch in leitungsvermittelten Netzen eine Fehlererkennung zu ermöglichen. Anschließend folgt ein punktierter Faltungscode mit der Ausgangsbitrate $22.8 \ \rm kbit/s$. Die Gesamtcoderate beträgt somit etwa $42.1\%$.
- Beim 3G–Mobilfunksystem UMTS (Universal Mobile Telecommunications System) verwendet man je nach den Randbedingungen (guter/schlechter Kanal, wenige/viele Teilnehmer in der Zelle) einen Faltungscode oder einen Turbocode (darunter versteht man per se die Verkettung zweier Faltungscodierer). Beim 4G–Mobilfunksystem LTE (Long Term Evolution) verwendet man für kurze Kontrollsignale einen Faltungscode und für die längeren Payload-Daten einen Turbocode.
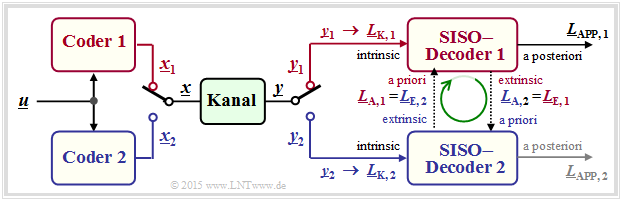
Die Grafik zeigt die Grundstruktur eines parallel verketteten Codiersystems. Alle Vektoren bestehen aus $n$ Elementen: $\underline{L} = (L(1), \ \text{...}\hspace{0.05cm} , \ L(n))$. Die Berechnung aller $L$–Werte geschieht also auf Symbolebene. Nicht dargestellt ist hier der Interleaver, der zum Beispiel bei den Turbocodes obligatorisch ist.
- Die Codesequenzen $\underline{x}_1$ und $\underline{x}_2$ werden zur gemeinsamen Übertragung über den Kanal durch einen Multiplexer zum Vektor $\underline{x}$ zusammengefügt. Am Empfänger wird die Sequenz $\underline{y}$ wieder in die Einzelteile $\underline{y}_1$ und $\underline{y}_2$ zerlegt. Daraus werden die Kanal–$L$–Werte $\underline{L}_{\rm K,\hspace{0.05cm}1} $ und $\underline{L}_{\rm K,\hspace{0.05cm}2}$ gebildet.
- Der symbolweise Decoder ermittelt entsprechend der vorne beschriebenen Vorgehensweise die extrinsischen $L$–Werte $\underline{L}_{\rm E,\hspace{0.05cm} 1}$ und $\underline{L}_{\rm E,\hspace{0.05cm} 2}$, die gleichzeitig die Apriori–Informationen $\underline{L}_{\rm A,\hspace{0.05cm} 2}$ und $\underline{L}_{\rm A,\hspace{0.05cm} 1}$ für den jeweils anderen Decoder darstellen.
- Nach ausreichend vielen Iterationen (also dann, wenn ein Abbruchkriterium erfüllt ist) liegt am Decoderausgang der Vektor der Aposteriori–Werte ⇒ $\underline{L}_{\rm APP}$ an. Im Beispiel wird willkürlich der Wert im oberen Zweig genommen. Möglich wäre aber auch der untere $L$–Wert.
Das obige Modell gilt insbesondere auch für die Decodierung der Turbo–Codes gemäß dem Kapitel Grundlegendes zu den Turbocodes.
Aufgaben zum Kapitel
Aufgabe 4.1: Zum „Log Likelihood Ratio”
Aufgabe 4.1Z: L–Werte des BEC–Modells
Aufgabe 4.2: Kanal–LLR bei AWGN
Aufgabe 4.3: Iterative Decodierung beim BSC
Aufgabe 4.3Z: Umrechnungen von L–Wert und S–Wert
Aufgabe 4.4: Extrinsische L–Werte beim SPC
Aufgabe 4.4Z: Ergänzung zur Aufgabe 4.4
Aufgabe 4.5: Nochmals zu den extrinsischen L–Werten
Aufgabe 4.5Z: Tangens Hyperbolikus und Inverse
Quellenverzeichnis