Difference between revisions of "Channel Coding/Soft-in Soft-Out Decoder"
| Line 166: | Line 166: | ||
== Symbol-wise soft in soft out decoding == | == Symbol-wise soft in soft out decoding == | ||
<br> | <br> | ||
| − | + | We now assume a $(n, \ k)$–block code where the codeword $\underline{x} = (x_1, \ \text{...} \ , \ x_n)$ is corrupted by the channel into the received word $\underline{y} = (y_1, \ \text{...} \ , \ y_n)$ . | |
| − | * | + | *For long codes, a <i>maximum a posteriori block-level decision</i> – is short: <b>[[Channel_Coding/Channel_Models_and_Decision_Structures#Criteria_.C2.BBMaximum-a-posteriori.C2.AB_and_.C2.BBMaximum-Likelihood.C2.AB|$\text{ "block wise MAP"}$]]</b> – very elaborate. |
| − | * | + | *One would have to find among the $2^k $ allowable codewords $\underline{x}_j ∈ \mathcal{C}$ the one with the greatest probability of inference ( <i>A Posteriori Probability</i>, APP). |
| − | * | + | *The codeword to output $\underline{z}$ in this case would be $\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}j} \hspace{0.03cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}j} |\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.$ |
| − | [[File:P ID2981 KC T 4 1 S3a v6.png|center|frame| | + | [[File:P ID2981 KC T 4 1 S3a v6.png|center|frame|Model of symbol-wise soft in soft out decoding|class=fit]] |
| − | + | A second possibility is decoding on bit level. The represented symbol-wise (or bit-wise) $\text{soft in soft out decoder}$ has the exercise to decode all codeword bits $x_i ∈ \{0, \, 1\}$ according to maximum inference probability (APP) ${\rm Pr}(x_i | \underline{y})$ . With the running variable $i = 1, \text{...} , \ n$ holds in this case: | |
| − | * | + | *The corresponding LLR for the $i$th code bit is: |
::<math>L_{\rm APP} (i) = L(x_i\hspace{0.05cm}|\hspace{0.05cm}\underline{y}) = | ::<math>L_{\rm APP} (i) = L(x_i\hspace{0.05cm}|\hspace{0.05cm}\underline{y}) = | ||
{\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x_i = 0\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}{{\rm Pr}(x_i = 1\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}\hspace{0.05cm} . </math> | {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x_i = 0\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}{{\rm Pr}(x_i = 1\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}\hspace{0.05cm} . </math> | ||
| − | * | + | *The decoder works iteratively. At initialization $($indicated in the diagram by the parameter $I = 0)$ is $L_{\rm APP}(i) = L_{\rm K}(i)$, where the channel LLR $L_{\rm K}(i)$ is given by the received value $y_i$ .<br> |
| − | * | + | *In addition, the extrinsic LLR $L_{\rm E}(i)$ is calculated, which quantifies the total information provided by all other bits $(j ≠ i)$ due to the code–properties about the considered $i$th bit.<br> |
| − | * | + | *At the next iteration $($ab $I = 1)$ $L_{\rm E}(i)$ is taken into account in the computation of $L_{\rm APP}(i)$ as apriori information $L_{\rm A}(i)$ . Thus, for the new a posteriori LLR in iteration $I + 1$ holds: |
::<math>L_{\hspace{0.1cm}\rm APP}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm A}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm E}^{(I)} (i)\hspace{0.05cm} . </math> | ::<math>L_{\hspace{0.1cm}\rm APP}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm A}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm E}^{(I)} (i)\hspace{0.05cm} . </math> | ||
| − | * | + | *The iterations continue until all absolute values $|L_{\rm APP}(i)|$ are greater than a given value. The most likely codeword $\underline{z}$ is then obtained from the signs of all $L_{\rm APP}(i)$, with $i = 1, \ \text{...} , \ n$.<br> |
| − | * | + | *For a [[Channel_Coding/General_Description_of_Linear_Block_Codes#Systematic_Codes| "systematic code"]] the first $k$ bits of $\underline{z}$ indicate the information word being searched for, which will most likely match the message $\underline{u}$ being sent.<br><br> |
| − | + | This description of the SISO decoder after [Bos98]<ref name='Bos98'>Bossert, M.: ''Kanalcodierung.'' Stuttgart: B. G. Teubner, 1998.</ref> is intended at this point primarily to clarify the different $L$–values. One recognizes the large potential of the symbol-wise decoding only in connection with [[Channel_Coding/Soft-in_Soft-Out_Decoder#Basic_structure_of_concatenated_coding_systems| "concatenated coding systems"]].<br> | |
| − | == | + | == Calculation of extrinsic LLRs == |
<br> | <br> | ||
| − | + | The difficulty in symbol-wise iterative decoding is generally the provision of the extrinsic LLRs $L_{\rm E}(i)$. For a code of length $n$ here, for the run variable: $i = 1, \ \text{...} , \ n$.<br> | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ The <b> extrinsic LLR</b> is a measure of the information that the other symbols $(j ≠ i)$ of the codeword provide about the $i$–th code symbol, expressed as a log likelihood ratio. We denote this characteristic value by $L_{\rm E}(i)$.}} |
| − | + | We now calculate the extrinsic LLRs $L_{\rm E}(i)$ for two example codes.<br> | |
$\text{Repetition Code}$ ⇒ ${\rm RC} \ (n, 1, n)$</b><br> | $\text{Repetition Code}$ ⇒ ${\rm RC} \ (n, 1, n)$</b><br> | ||
| − | + | A repetition code is characterized by the fact that all $n$ code symbols $x_i ∈ \{0, \, 1\}$ are identical. The extrinsic LLR for the $i$&th symbol is very easy to specify here and is: | |
::<math>L_{\rm E}(i) = \hspace{0.05cm}\sum_{j \ne i} \hspace{0.1cm} L_j | ::<math>L_{\rm E}(i) = \hspace{0.05cm}\sum_{j \ne i} \hspace{0.1cm} L_j | ||
| Line 214: | Line 214: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | * | + | *If the sum over all $L_{j ≠ i}$ is positive, this implies a preference for the decision $x_i = 0$ from the point of view of the other LLR. |
| − | * | + | *On the other hand, if the sum is negative $x_i = 1$ is more likely. |
| − | *$L_{\rm E}(i) = 0$ | + | *$L_{\rm E}(i) = 0$ does not allow prediction.<br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 5:}$ We consider the decoding of the repetition code $\text{RC (4, 1,4)}$. We make three different assumptions for the <i>Log Likelihood Ratio</i> $\underline{L}_{\rm A}^{(I=0)} = \underline{L}_{\rm APP}$ . |
| − | [[File:P ID3094 KC T 4 4 S3a neu v2.png|right|frame| | + | [[File:P ID3094 KC T 4 4 S3a neu v2.png|right|frame|Decoding example $\rm (A)$ for the ${\rm RC} \ (4, 1, 4)$|class=fit]] |
| − | $\text{ | + | $\text{Decoding example (A):}$ |
:$$\underline{L}_{\rm APP} = (+1, -1, +3, -1)\text{:}$$ | :$$\underline{L}_{\rm APP} = (+1, -1, +3, -1)\text{:}$$ | ||
::$$L_{\rm E}(1) = -1+3-1 = +1\hspace{0.05cm},$$ | ::$$L_{\rm E}(1) = -1+3-1 = +1\hspace{0.05cm},$$ | ||
| Line 231: | Line 231: | ||
:$$\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm E}^{(I=0)}= (+1, +3, -1, +3) | :$$\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm E}^{(I=0)}= (+1, +3, -1, +3) | ||
\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm A}^{(I=1)}=\underline{L}_{\rm A}^{(I=0)}+ \underline{L}_{\rm E}^{(I=0)}= (+2, +2, +2, +2)$$ | \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm A}^{(I=1)}=\underline{L}_{\rm A}^{(I=0)}+ \underline{L}_{\rm E}^{(I=0)}= (+2, +2, +2, +2)$$ | ||
| − | * | + | *At the beginning $(I=0)$ the positive $L_{\rm E}$–values indicate $x_1 = 0$, $x_2 = 0$ and $x_4 = 0$ while $x_3 =1$ is more likely. |
| − | * | + | *Already after one iteration $(I=1)$ all $L_{\rm A}$–values are positive ⇒ information bit is decoded as $u = 0$ . |
| − | * | + | *Further iterations yield nothing.<br> |
| − | [[File:P ID3096 KC T 4 4 S3c neu v1.png|right|frame| | + | [[File:P ID3096 KC T 4 4 S3c neu v1.png|right|frame|Decoding example $\rm (B)$ for the ${\rm RC} \ (4, 1, 4)$]] |
| − | $\text{ | + | $\text{Decoding example (B):}$ |
$$\underline{L}_{\rm APP} = (+1, +1, -4, +1)\text{:}$$ | $$\underline{L}_{\rm APP} = (+1, +1, -4, +1)\text{:}$$ | ||
$$\underline{L}_{\rm E}^{(I=0)} = \ (-2, -2, +3, -2)$$ | $$\underline{L}_{\rm E}^{(I=0)} = \ (-2, -2, +3, -2)$$ | ||
| − | * | + | *Although three signs were wrong at the beginning, after two iterations all $L_{\rm A}$–values (LLR) are negative. |
| − | * | + | *The information bit is decoded as $u = 1$ . |
| − | [[File:P ID3095 KC T 4 4 S3b neu v1.png|right|frame| | + | [[File:P ID3095 KC T 4 4 S3b neu v1.png|right|frame|Decoding example $\rm (C)$ for the ${\rm RC} \ (4, 1, 4)$]]<br> |
| − | $\text{ | + | $\text{Decoding example (C):}$ |
$$\underline{L}_{\rm APP} = (+1, +1, -3, +1)\text{:}$$ | $$\underline{L}_{\rm APP} = (+1, +1, -3, +1)\text{:}$$ | ||
$$\underline{L}_{\rm E}^{(I=0)} = (-1, -1, +3, -1)$$ | $$\underline{L}_{\rm E}^{(I=0)} = (-1, -1, +3, -1)$$ | ||
| − | * | + | *All $L_{\rm A}$–values (LLR) are zero already after one iteration. |
| − | * | + | *The information bit cannot be decoded, although the initial situation was not much worse than with $\rm (B)$. |
| − | * | + | *Further iterations bring nothing here either.<br>}} |
| − | + | $\text{Single Parity–check code}$ ⇒ ${\rm SPC} \ (n, \ n \, -1, \ 2)$ | |
| − | $\text{Single Parity–check | ||
<br> | <br> | ||
| − | + | For each <i>Single Parity–check Code</i> the number of ones in each codeword is even. Or, put another way, For each codeword $\underline{x}$ the [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding|"Hamming weight"]] $w_{\rm H}(\underline{x})$ is even.<br> | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ Let the codeword $\underline{x}^{(–i)}$ contain all symbols except $x_i$ ⇒ vector of length $n -1$. Thus, the $\text{extrinsic }LLR$ is with respect to the $i$–th symbol when $\underline{x}$ was received: |
::<math>L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} \vert\hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} \vert \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} | ::<math>L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} \vert\hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} \vert \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | As will be shown in the [[Aufgaben:Exercise_4.4:_Extrinsic_L-Values_at_SPC|"Task 4.4"]] , it is also possible to write for this: | |
::<math>L_{\rm E}(i) = 2 \cdot {\rm tanh}^{-1} \hspace{0.1cm} \left [ \prod\limits_{j \ne i}^{n} \hspace{0.15cm}{\rm tanh}(L_j/2) \right ] | ::<math>L_{\rm E}(i) = 2 \cdot {\rm tanh}^{-1} \hspace{0.1cm} \left [ \prod\limits_{j \ne i}^{n} \hspace{0.15cm}{\rm tanh}(L_j/2) \right ] | ||
| Line 274: | Line 273: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 6:}$ We assume <i>Single Parity–check code</i> with $n = 3, \ k = 2$ ⇒ briefly ${\rm SPC} \ (3, \ 2, \ 2)$ from. |
| − | + | The $2^k = 4$ valid codewords $\underline{x} = \{x_1, x_2, x_3\}$ are for bipolar description ⇒ $x_i ∈ \{±1\}$: | |
| − | [[File:P ID3098 KC T 4 1 S3e v1.png|right|frame| | + | [[File:P ID3098 KC T 4 1 S3e v1.png|right|frame|Decoding example for the ${\rm SPC} \ (3, 2, 2)$|class=fit]] |
:$$ \underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{-0.05cm}, $$ | :$$ \underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{-0.05cm}, $$ | ||
| Line 284: | Line 283: | ||
:$$\underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} +1)\hspace{-0.05cm}. $$ | :$$\underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} +1)\hspace{-0.05cm}. $$ | ||
| − | + | So, with this code, the product $x_1 \cdot x_2 \cdot x_3$ is always positive.<br> | |
| − | + | The above table shows the decoding process for $\underline{L}_{\rm APP} = (+2.0, +0.4, \, –1.6)$. The hard decision according to the signs of $L_{\rm APP}(i)$ would yield here $(+1, +1, \, -1)$, thus no valid codeword of ${\rm SP}(3, \ 2, \ 2)$.<br> | |
| − | + | On the right side of the table, the corresponding extrinsic LLRs are entered:<br> | |
::<math>L_{\rm E}(1) = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} | ::<math>L_{\rm E}(1) = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} | ||
| Line 297: | Line 296: | ||
\left [ {\rm tanh} (1.0) \cdot {\rm tanh} (0.2)\hspace{0.05cm}\right ] = +0.151\hspace{0.05cm}.</math> | \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (0.2)\hspace{0.05cm}\right ] = +0.151\hspace{0.05cm}.</math> | ||
| − | + | The second equation can be interpreted as follows: | |
| − | * $L_{\rm APP}(1) = +2.0$ | + | * $L_{\rm APP}(1) = +2.0$ and $L_{\rm APP}(3) = \, -1.6$ state that the first bit is more likely to be $+1$ than $-1$ and the third bit is more likely to be $-1$ than $+1$. The reliability (the amount) is slightly greater for the first bit than for the third.<br> |
| − | * | + | *The extrinsic information $L_{\rm E}(2) = \, -0.518$ considers only the information of bit 1 and bit 3 about bit 2. From their point of view, the second bit is a $-1$ with reliability $0.518$.<br> |
| − | * | + | *The $y_2$ value derived from the received LLR ⇒ $L_{\rm APP}(2) = +0.4$ has suggested a $+1$ for the second bit. The discrepancy is resolved here already in the iteration $I = 1$ .<br> |
| − | * | + | *Decided here for the codeword $\underline{x}_1$. For $0.518 < L_{\rm APP}(2) < 1.6$ the result $\underline{x}_1$ would only be available after several iterations. For $L_{\rm APP}(2) > 1.6$ on the other hand, the decoder returns $\underline{x}_0$.}}<br> |
| − | == | + | == BCJR decoding: Forward-backward algorithm == |
<br> | <br> | ||
Ein Beispiel für die iterative Decodierung von Faltungscodes ist der <i>BCJR–Algorithmus</i>, benannt nach dessen Erfindern L. R. Bahl, J. Cocke, F. Jelinek und J. Raviv ⇒ [BCJR74]<ref name='BCJR74'>Bahl, L.R.; Cocke, J.; Jelinek, F.; Raviv, J.: ''Optimal Decoding of Linear Codes for Minimizing Symbol Error Rate.'' In: IEEE Transactions on Information Theory, Vol. IT-20, S. 284-287, 1974.</ref>. Der Algorithmus weist viele Parallelen zur sieben Jahren älteren Viterbi–Decodierung auf, doch auch einige signifikante Unterschiede: | Ein Beispiel für die iterative Decodierung von Faltungscodes ist der <i>BCJR–Algorithmus</i>, benannt nach dessen Erfindern L. R. Bahl, J. Cocke, F. Jelinek und J. Raviv ⇒ [BCJR74]<ref name='BCJR74'>Bahl, L.R.; Cocke, J.; Jelinek, F.; Raviv, J.: ''Optimal Decoding of Linear Codes for Minimizing Symbol Error Rate.'' In: IEEE Transactions on Information Theory, Vol. IT-20, S. 284-287, 1974.</ref>. Der Algorithmus weist viele Parallelen zur sieben Jahren älteren Viterbi–Decodierung auf, doch auch einige signifikante Unterschiede: | ||
| − | *Während Viterbi die Gesamtsequenz schätzt ⇒ [[Channel_Coding/ | + | *Während Viterbi die Gesamtsequenz schätzt ⇒ [[Channel_Coding/Channel_Models_and_Decision_Structures#Definitions_of_the_different_optimal_receivers| $\text{"block–wise Maximum Likelihood"}$]], minimiert der BCJR–Algorithmus die Bitfehlerwahrscheinlichkeit ⇒ [[Channel_Coding/Channel_Models_and_Decision_Structures#Definitions_of_the_different_optimal_receivers|$\text{"bit–wise MAP"}$]].<br> |
*Der Viterbi–Algorithmus kann (in seiner ursprünglichen Form) keine Softinformation verarbeiten. Dagegen gibt der BCJR–Algorithmus bei jeder Iteration für jedes einzelne Symbol (Bit) einen Zuverlässigkeitswert an, der bei späteren Iterationen berücksichtigt wird.<br> | *Der Viterbi–Algorithmus kann (in seiner ursprünglichen Form) keine Softinformation verarbeiten. Dagegen gibt der BCJR–Algorithmus bei jeder Iteration für jedes einzelne Symbol (Bit) einen Zuverlässigkeitswert an, der bei späteren Iterationen berücksichtigt wird.<br> | ||
| Line 317: | Line 316: | ||
Die Abbildung soll – fast unzulässig vereinfacht – die unterschiedliche Vorgehensweise von Viterbi–Algorithmus (links) und BCJR–Algorithmus (rechts) verdeutlichen. Zugrunde liegt ein Faltungscode mit dem Gedächtnis $m = 1$ und der Länge $L = 4$ ⇒ Gesamtlänge (mit Terminierung) $L' = 5$. | Die Abbildung soll – fast unzulässig vereinfacht – die unterschiedliche Vorgehensweise von Viterbi–Algorithmus (links) und BCJR–Algorithmus (rechts) verdeutlichen. Zugrunde liegt ein Faltungscode mit dem Gedächtnis $m = 1$ und der Länge $L = 4$ ⇒ Gesamtlänge (mit Terminierung) $L' = 5$. | ||
| − | *Der Viterbi–Algorithmus sucht und findet den wahrscheinlichsten Pfad von ${\it \Gamma}_0(S_0)$ nach ${\it \Gamma}_5(S_0)$, nämlich $S_0 → S_1 → S_0 → S_0 → S_1→ S_0 $. Wir verweisen auf die Musterlösung zur [[Aufgaben: | + | *Der Viterbi–Algorithmus sucht und findet den wahrscheinlichsten Pfad von ${\it \Gamma}_0(S_0)$ nach ${\it \Gamma}_5(S_0)$, nämlich $S_0 → S_1 → S_0 → S_0 → S_1→ S_0 $. Wir verweisen auf die Musterlösung zur [[Aufgaben:Exercise_3.09Z:_Viterbi_Algorithm_again|"Aufgabe 3.9Z"]].<br><br> |
Die Skizze für den BCJR–Algorithmus verdeutlicht die Gewinnung des extrinsischen $L$–Wertes für das dritte Symbol ⇒ $L_{\rm E}(3)$. Der relevante Bereich im Trellis ist schraffiert: | Die Skizze für den BCJR–Algorithmus verdeutlicht die Gewinnung des extrinsischen $L$–Wertes für das dritte Symbol ⇒ $L_{\rm E}(3)$. Der relevante Bereich im Trellis ist schraffiert: | ||
Revision as of 21:15, 22 October 2022
Contents
- 1 # OVERVIEW OF THE FOURTH MAIN CHAPTER #
- 2 Hard Decision vs. Soft Decision
- 3 Reliability information - Log Likelihood Ratio
- 4 Symbol-wise soft in soft out decoding
- 5 Calculation of extrinsic LLRs
- 6 BCJR decoding: Forward-backward algorithm
- 7 Basic structure of concatenated coding systems
- 8 Aufgaben zum Kapitel
- 9 Quellenverzeichnis
# OVERVIEW OF THE FOURTH MAIN CHAPTER #
The last main chapter of the channel coding book describes iterative decoding techniques as used in most of today's (2017) communication systems. This is due to the following reasons:
- To approach the channel capacity, one needs very long codes.
- But for long codes, blockwise maximum likelihood decoding is almost impossible.
The decoder complexity can be significantly reduced with almost the same quality if two (or more) short channel codes are linked together and the newly acquired (soft) information is exchanged between the decoders at the receiver in several steps - i.e. iteratively.
The breakthrough in the field came in the early 1990s with the invention of turbo codes by "Claude Berrou" and shortly thereafter with the rediscovery of low-density parity-check codes by wikipedia.org/wiki/David_J._C._MacKay "David J. C. MacKay" and "Radford M. Neal", after the LDPC codes developed as early as 1961 by "Robert G. Gallager" had been forgotten in the meantime.
Specifically, the fourth main chapter discusses:
- a comparison of Hard Decision and Soft Decision,
- the quantification of reliability information by log likelihood ratios (LLR),
- the principle of symbol-wise soft in soft out (SISO) decoding,
- the definition of apriori L value, a posteriori L-value and extrinsic L value,
- the basic structure of serially concatenated and parallel concatenated coding systems, respectively,
- the characteristics of product codes and their hard decision decoding,
- the basic structure, decoding algorithm and performance of turbo codes,
- basic information on the low-density parity-check codes and their applications.
Hard Decision vs. Soft Decision
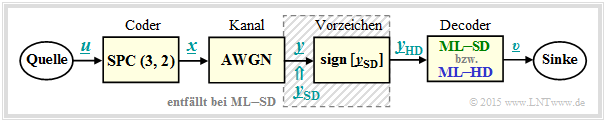
To introduce the topic discussed here, let us consider the following message transmission system with coding.
In the following, all symbols are given in bipolar representation: "$0$" → "$+1$" and "$1$" → "$-1$".
- The symbol sequence $\underline{u} = (u_1, \ u_2)$ is assigned to the code sequence $\underline{x} = (x_1, \ x_2, \ x_3) = (u_1, \ u_2, \ p)$ where for the parity bit $p = u_1 ⊕ u_2$ holds ⇒ "Single Parity–check Code" ⇒ ${\rm SPC} (3, 2, 2)$.
- The "AWGN–channel" changes the binary symbols $x_i ∈ \{+1, \ –1\}$ to real-valued output values $y_i$, for example according to $\text{channel 4}$ the table below: $x_1 = +1$ ⇒ $y_1 = +0. 9$, $x_2 = \, -1$ ⇒ $y_2 = +0.1$ and $x_3 = \, -1$ ⇒ $y_3 = +0.1$.
- Decoding is done according to the criterion "Maximum-Likelihood" $\text{(blockwise ML)}$, distinguishing between hard decision $\rm {(ML–HD)}$ and soft decision $\rm {(ML–SD)}$ .
- The whole block diagram corresponds to $\rm ML–HD$. Here, only the signs of the AWGN output values ⇒ $y_{\rm HD, \ \it i} = {\rm sign}\big [y_{\rm SD, \ \it i}\big ]$ are evaluated for decoding. In soft decision $\rm {(ML–SD)}$ one omits the shaded block and directly evaluates the continuous value input variables $y_{\rm SD, \ \it i}$ .
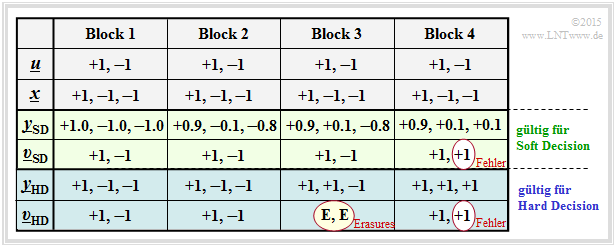
For all columns of this table it is assumed:
- the message block $\underline{u} = (0, 1)$, bipolar representable as $(+1, \, –1)$,
- the ${\rm SPC} \ (3, 2)$–coded block $\underline{x} = (0, 1, 1)$ respectively in bipolar representation $(+1, \, -1, \, -1)$.
Thus, the four columns differ only by different AWGN realizations.
$\text{Definition:}$ From the example table you can see:
- $\text{Hard Decision:}$ The symbol sequence $\underline{v}_{\rm HD}$ results from the hard decided channel values $\underline{y}_{\rm HD}$ (blue background).
In our example, only the constellations according to $\text{channel 1}$ and $\text{channel 2}$ are decoded without errors.
- $\text{Soft Decision:}$ The symbol sequence $\underline{v}_{\rm SD}$ results from the "soft" channel output values $\underline{y}_{\rm SD}$ (green background).
Now, in this example, it is also correctly decided at $\text{channel 3}$
The entries in the example table above are to be interpreted as follows:
- For ideal channel ⇒ $\text{channel 1}$ ⇒ $\underline{x} = \underline{y}_{\rm SD} = \underline{y}_{\rm HD}$ there is no difference between the (blue) conventional hard decision variant $\rm {(ML–HD)}$ and the (green) soft decision variant $\rm {(ML–SD)}$.
- Setting according $\text{channel 2}$ demonstrates low signal distortions. Because of $\underline{y}_{\rm HD} = \underline{x}$ (which means that the channel does not distort the signs) also $\rm ML–HD$ gives the correct result $\underline{v}_{\rm HD} = \underline{u}$.
- For $\text{channel 3}$ there is $\underline{y}_{\rm HD} ≠ \underline{x}$ and there is also no ${\rm SPC} \ (3, 2)$–assignment $\underline{u}$ ⇒ $\underline{y}_{\rm HD}$. The ML–decoder reports here by outputting $\underline{v}_{\rm HD} = \rm (E, \ E)$ that it failed in decoding this block. "$\rm E$" stands for "Erasure" .
- Also the soft decision decoder recognizes that decoding based on the signs does not work. Based on the $\underline{y}_{\rm SD}$–values, however, it recognizes that with high probability the second bit has been corrupted and decides to use the correct symbol sequence $\underline{v}_{\rm SD} = (+1, \, -1) = \underline{u}$.
- In $\text{channel 4}$ both the signs of bit 2 and bit 3 are changed by the AWGN–channel, leading to the result $\underline{v}_{\rm HD} = (+1, +1) ≠ \underline{u}(+1, \, -1)$ ⇒ a block error and a bit error at the same time. Also the soft decision decoder gives the same wrong result here.
The decoding variant "ML–SD" also offers the advantage over "ML–HD" that it is relatively easy to assign a reliability value to each decoding result (in the above table, however, this is not specified). This reliability value
- would have its maximum value at $\text{channel 1}$ ,
- would be significantly smaller for $\text{channel 2}$ ,
- would be close to zero for $\text{channel 3}$ and $\text{channel 4}$ .
Reliability information - Log Likelihood Ratio
Let $x ∈ \{+1, \, -1\}$ be a binary random variable with probabilities ${\rm Pr}(x = +1)$ and ${\rm Pr}(x = \, -1)$. For coding theory, it proves convenient in terms of computation times to use the natural logarithm of the quotient instead of the probabilities ${\rm Pr}(x = ±1)$ .
$\text{Definition:}$ The log likelihood ratio (LLR) of the random variable $x ∈ \{+1, \, -1\}$ is:
- \[L(x)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(x = +1)}{ {\rm Pr}(x = -1)}\hspace{0.05cm}.\]
For unipolar/symbolic representation $(+1 → 0$ and $-1 → 1)$ applies accordingly with $\xi ∈ \{0, \, 1\}$:
- \[L(\xi)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(\xi = 0)}{ {\rm Pr}(\xi = 1)}\hspace{0.05cm}.\]
Below is given the nonlinear relationship between ${\rm Pr}(x = ±1)$ and $L(x)$ . Replacing ${\rm Pr}(x = +1)$ with ${\rm Pr}(\xi = 0)$, the middle row gives the $L$–value of the unipolar random variable $\xi$.
You can see:
- The more likely random value of $x ∈ \{+1, \, -1\}$ is given by the sign ⇒ ${\rm sign} \ L(x)$ given.
- In contrast, the absolute value ⇒ $|L(x)|$ indicates the reliability for the result ${\rm sign}(L(x))$ .
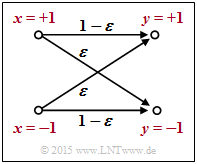
$\text{Example 1:}$ We consider the outlined "BSC model" with bipolar representation. Here, with the corruption probability $\varepsilon = 0.1$ and the two random variables $x ∈ \{+1, \, -1\}$ and $y ∈ \{+1, \, -1\}$ at the input and output of the channel:
- \[L(y\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(y\hspace{0.05cm}\vert\hspace{0.05cm}x = +1) }{ {\rm Pr}(y\hspace{0.05cm}\vert\hspace{0.05cm}x = -1)} = \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} \big[(1 - \varepsilon)/\varepsilon \big]\\ {\rm ln} \hspace{0.15cm}\big [\varepsilon/(1 - \varepsilon)\big] \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm} y = +1, \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = -1. \\ \end{array}\]
For example, $\varepsilon = 0.1$ results in the following numerical values (compare upper table):
- \[L(y = +1\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{0.9}{0.1} = +2.197\hspace{0.05cm}, \hspace{0.8cm} L(y = -1\hspace{0.05cm}\vert\hspace{0.05cm}x) = -2.197\hspace{0.05cm}.\]
This example shows that the so-called LLR algebra can also be applied to conditional probabilities.
In the "Exercise 4.1Z" the BEC–model is described in a similar way.
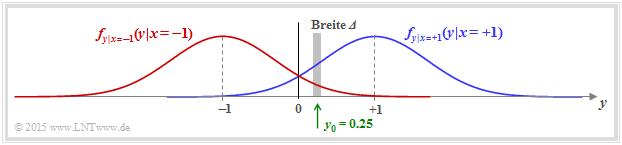
$\text{Example 2:}$ In another example, now consider the "AWGN channel" with the conditional probability density functions
- \[f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y-1)^2}/(2\sigma^2) } \hspace{0.05cm},\]
- \[f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=-1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y+1)^2}/(2\sigma^2) } \hspace{0.05cm}.\]
In the graphic, two exemplary Gaussian functions are shown as blue and red curves, respectively.
The total PDF of the output signal $y$ is obtained from the (equally) weighted sum:
- \[f_{y } \hspace{0.05cm} (y ) = 1/2 \cdot \big [ f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 ) \hspace{0.1cm} + \hspace{0.1cm} f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert \hspace{0.05cm}x=-1 ) \big ] \hspace{0.05cm}.\]
We now calculate the probability that the received value $y$ lies in a (very) narrow interval of width $\Delta$ around $y_0 = 0.25$ . One obtains approximately
- \[{\rm Pr} (\vert y - y_0\vert \le{\it \Delta}/2 \hspace{0.05cm} \Big \vert \hspace{0.05cm}x=+1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2) } \hspace{0.05cm},\]
- \[{\rm Pr} (\vert y - y_0\vert \le {\it \Delta}/2 \hspace{0.05cm} \Big \vert \hspace{0.05cm}x=-1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2) } \hspace{0.05cm}.\]
The slightly larger vertical lines denote the conditions, the smaller ones the absolute value.
The LLR of the conditional probability in the forward direction $($meaning: output $y$ for a given input $x)$ is thus obtained as the logarithm of the quotient of both expressions:
- \[L(y = y_0\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \left [ \frac{{\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2)}}{{\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2)}} \right ] = {\rm ln} \left [ {\rm e} ^{ - [ {(y_0-1)^2}+{(y_0+1)^2}]/(2\sigma^2)} \right ] = \frac{(y_0+1)^2-(y_0-1)^2}{2\cdot \sigma^2} = \frac{2 \cdot y_0}{\sigma^2}\hspace{0.05cm}. \]
If we now replace the auxiliary $y_0$ with the (general) random $y$ at the AWGN output, the final result is:
- \[L(y \hspace{0.05cm}\vert\hspace{0.05cm}x) = {2 \cdot y}/{\sigma^2} =K_{\rm L} \cdot y\hspace{0.05cm}. \]
Here $K_{\rm L} = 2/\sigma^2$ is a constant that depends solely on the standard deviation of the Gaussian
.
Symbol-wise soft in soft out decoding
We now assume a $(n, \ k)$–block code where the codeword $\underline{x} = (x_1, \ \text{...} \ , \ x_n)$ is corrupted by the channel into the received word $\underline{y} = (y_1, \ \text{...} \ , \ y_n)$ .
- For long codes, a maximum a posteriori block-level decision – is short: $\text{ "block wise MAP"}$ – very elaborate.
- One would have to find among the $2^k $ allowable codewords $\underline{x}_j ∈ \mathcal{C}$ the one with the greatest probability of inference ( A Posteriori Probability, APP).
- The codeword to output $\underline{z}$ in this case would be $\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}j} \hspace{0.03cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}j} |\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.$
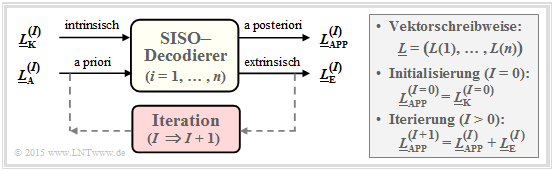
A second possibility is decoding on bit level. The represented symbol-wise (or bit-wise) $\text{soft in soft out decoder}$ has the exercise to decode all codeword bits $x_i ∈ \{0, \, 1\}$ according to maximum inference probability (APP) ${\rm Pr}(x_i | \underline{y})$ . With the running variable $i = 1, \text{...} , \ n$ holds in this case:
- The corresponding LLR for the $i$th code bit is:
- \[L_{\rm APP} (i) = L(x_i\hspace{0.05cm}|\hspace{0.05cm}\underline{y}) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x_i = 0\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}{{\rm Pr}(x_i = 1\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}\hspace{0.05cm} . \]
- The decoder works iteratively. At initialization $($indicated in the diagram by the parameter $I = 0)$ is $L_{\rm APP}(i) = L_{\rm K}(i)$, where the channel LLR $L_{\rm K}(i)$ is given by the received value $y_i$ .
- In addition, the extrinsic LLR $L_{\rm E}(i)$ is calculated, which quantifies the total information provided by all other bits $(j ≠ i)$ due to the code–properties about the considered $i$th bit.
- At the next iteration $($ab $I = 1)$ $L_{\rm E}(i)$ is taken into account in the computation of $L_{\rm APP}(i)$ as apriori information $L_{\rm A}(i)$ . Thus, for the new a posteriori LLR in iteration $I + 1$ holds:
- \[L_{\hspace{0.1cm}\rm APP}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm A}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm E}^{(I)} (i)\hspace{0.05cm} . \]
- The iterations continue until all absolute values $|L_{\rm APP}(i)|$ are greater than a given value. The most likely codeword $\underline{z}$ is then obtained from the signs of all $L_{\rm APP}(i)$, with $i = 1, \ \text{...} , \ n$.
- For a "systematic code" the first $k$ bits of $\underline{z}$ indicate the information word being searched for, which will most likely match the message $\underline{u}$ being sent.
This description of the SISO decoder after [Bos98][1] is intended at this point primarily to clarify the different $L$–values. One recognizes the large potential of the symbol-wise decoding only in connection with "concatenated coding systems".
Calculation of extrinsic LLRs
The difficulty in symbol-wise iterative decoding is generally the provision of the extrinsic LLRs $L_{\rm E}(i)$. For a code of length $n$ here, for the run variable: $i = 1, \ \text{...} , \ n$.
$\text{Definition:}$ The extrinsic LLR is a measure of the information that the other symbols $(j ≠ i)$ of the codeword provide about the $i$–th code symbol, expressed as a log likelihood ratio. We denote this characteristic value by $L_{\rm E}(i)$.
We now calculate the extrinsic LLRs $L_{\rm E}(i)$ for two example codes.
$\text{Repetition Code}$ ⇒ ${\rm RC} \ (n, 1, n)$
A repetition code is characterized by the fact that all $n$ code symbols $x_i ∈ \{0, \, 1\}$ are identical. The extrinsic LLR for the $i$&th symbol is very easy to specify here and is:
- \[L_{\rm E}(i) = \hspace{0.05cm}\sum_{j \ne i} \hspace{0.1cm} L_j \hspace{0.3cm}{\rm mit}\hspace{0.3cm}L_j = L_{\rm APP}(j) \hspace{0.05cm}.\]
- If the sum over all $L_{j ≠ i}$ is positive, this implies a preference for the decision $x_i = 0$ from the point of view of the other LLR.
- On the other hand, if the sum is negative $x_i = 1$ is more likely.
- $L_{\rm E}(i) = 0$ does not allow prediction.
$\text{Example 5:}$ We consider the decoding of the repetition code $\text{RC (4, 1,4)}$. We make three different assumptions for the Log Likelihood Ratio $\underline{L}_{\rm A}^{(I=0)} = \underline{L}_{\rm APP}$ .
$\text{Decoding example (A):}$
- $$\underline{L}_{\rm APP} = (+1, -1, +3, -1)\text{:}$$
- $$L_{\rm E}(1) = -1+3-1 = +1\hspace{0.05cm},$$
- $$L_{\rm E}(2) = +1+3-1 = +3\hspace{0.05cm},$$
- $$L_{\rm E}(3) = +1-1 -1= -1\hspace{0.05cm},$$
- $$L_{\rm E}(4) = +1-1 +3 = +3\hspace{0.05cm}$$
- $$\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm E}^{(I=0)}= (+1, +3, -1, +3) \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm A}^{(I=1)}=\underline{L}_{\rm A}^{(I=0)}+ \underline{L}_{\rm E}^{(I=0)}= (+2, +2, +2, +2)$$
- At the beginning $(I=0)$ the positive $L_{\rm E}$–values indicate $x_1 = 0$, $x_2 = 0$ and $x_4 = 0$ while $x_3 =1$ is more likely.
- Already after one iteration $(I=1)$ all $L_{\rm A}$–values are positive ⇒ information bit is decoded as $u = 0$ .
- Further iterations yield nothing.
$\text{Decoding example (B):}$ $$\underline{L}_{\rm APP} = (+1, +1, -4, +1)\text{:}$$ $$\underline{L}_{\rm E}^{(I=0)} = \ (-2, -2, +3, -2)$$
- Although three signs were wrong at the beginning, after two iterations all $L_{\rm A}$–values (LLR) are negative.
- The information bit is decoded as $u = 1$ .
$\text{Decoding example (C):}$ $$\underline{L}_{\rm APP} = (+1, +1, -3, +1)\text{:}$$ $$\underline{L}_{\rm E}^{(I=0)} = (-1, -1, +3, -1)$$
- All $L_{\rm A}$–values (LLR) are zero already after one iteration.
- The information bit cannot be decoded, although the initial situation was not much worse than with $\rm (B)$.
- Further iterations bring nothing here either.
$\text{Single Parity–check code}$ ⇒ ${\rm SPC} \ (n, \ n \, -1, \ 2)$
For each Single Parity–check Code the number of ones in each codeword is even. Or, put another way, For each codeword $\underline{x}$ the "Hamming weight" $w_{\rm H}(\underline{x})$ is even.
$\text{Definition:}$ Let the codeword $\underline{x}^{(–i)}$ contain all symbols except $x_i$ ⇒ vector of length $n -1$. Thus, the $\text{extrinsic }LLR$ is with respect to the $i$–th symbol when $\underline{x}$ was received:
- \[L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} \vert\hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} \vert \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.\]
As will be shown in the "Task 4.4" , it is also possible to write for this:
- \[L_{\rm E}(i) = 2 \cdot {\rm tanh}^{-1} \hspace{0.1cm} \left [ \prod\limits_{j \ne i}^{n} \hspace{0.15cm}{\rm tanh}(L_j/2) \right ] \hspace{0.3cm}{\rm mit}\hspace{0.3cm}L_j = L_{\rm APP}(j) \hspace{0.05cm}.\]
$\text{Example 6:}$ We assume Single Parity–check code with $n = 3, \ k = 2$ ⇒ briefly ${\rm SPC} \ (3, \ 2, \ 2)$ from.
The $2^k = 4$ valid codewords $\underline{x} = \{x_1, x_2, x_3\}$ are for bipolar description ⇒ $x_i ∈ \{±1\}$:
- $$ \underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{-0.05cm}, $$
- $$\underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, $$
- $$\underline{x}_2 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} +1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, $$
- $$\underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} +1)\hspace{-0.05cm}. $$
So, with this code, the product $x_1 \cdot x_2 \cdot x_3$ is always positive.
The above table shows the decoding process for $\underline{L}_{\rm APP} = (+2.0, +0.4, \, –1.6)$. The hard decision according to the signs of $L_{\rm APP}(i)$ would yield here $(+1, +1, \, -1)$, thus no valid codeword of ${\rm SP}(3, \ 2, \ 2)$.
On the right side of the table, the corresponding extrinsic LLRs are entered:
- \[L_{\rm E}(1) = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (0.2) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.131\hspace{0.05cm}, \]
- \[L_{\rm E}(2) =2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.518\hspace{0.05cm}, \]
- \[L_{\rm E}(3) =2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (0.2)\hspace{0.05cm}\right ] = +0.151\hspace{0.05cm}.\]
The second equation can be interpreted as follows:
- $L_{\rm APP}(1) = +2.0$ and $L_{\rm APP}(3) = \, -1.6$ state that the first bit is more likely to be $+1$ than $-1$ and the third bit is more likely to be $-1$ than $+1$. The reliability (the amount) is slightly greater for the first bit than for the third.
- The extrinsic information $L_{\rm E}(2) = \, -0.518$ considers only the information of bit 1 and bit 3 about bit 2. From their point of view, the second bit is a $-1$ with reliability $0.518$.
- The $y_2$ value derived from the received LLR ⇒ $L_{\rm APP}(2) = +0.4$ has suggested a $+1$ for the second bit. The discrepancy is resolved here already in the iteration $I = 1$ .
- Decided here for the codeword $\underline{x}_1$. For $0.518 < L_{\rm APP}(2) < 1.6$ the result $\underline{x}_1$ would only be available after several iterations. For $L_{\rm APP}(2) > 1.6$ on the other hand, the decoder returns $\underline{x}_0$.
BCJR decoding: Forward-backward algorithm
Ein Beispiel für die iterative Decodierung von Faltungscodes ist der BCJR–Algorithmus, benannt nach dessen Erfindern L. R. Bahl, J. Cocke, F. Jelinek und J. Raviv ⇒ [BCJR74][2]. Der Algorithmus weist viele Parallelen zur sieben Jahren älteren Viterbi–Decodierung auf, doch auch einige signifikante Unterschiede:
- Während Viterbi die Gesamtsequenz schätzt ⇒ $\text{"block–wise Maximum Likelihood"}$, minimiert der BCJR–Algorithmus die Bitfehlerwahrscheinlichkeit ⇒ $\text{"bit–wise MAP"}$.
- Der Viterbi–Algorithmus kann (in seiner ursprünglichen Form) keine Softinformation verarbeiten. Dagegen gibt der BCJR–Algorithmus bei jeder Iteration für jedes einzelne Symbol (Bit) einen Zuverlässigkeitswert an, der bei späteren Iterationen berücksichtigt wird.
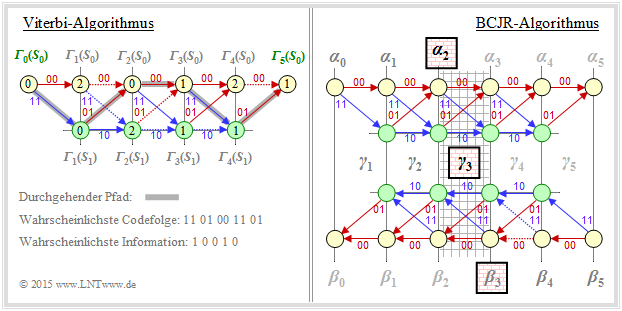
Die Abbildung soll – fast unzulässig vereinfacht – die unterschiedliche Vorgehensweise von Viterbi–Algorithmus (links) und BCJR–Algorithmus (rechts) verdeutlichen. Zugrunde liegt ein Faltungscode mit dem Gedächtnis $m = 1$ und der Länge $L = 4$ ⇒ Gesamtlänge (mit Terminierung) $L' = 5$.
- Der Viterbi–Algorithmus sucht und findet den wahrscheinlichsten Pfad von ${\it \Gamma}_0(S_0)$ nach ${\it \Gamma}_5(S_0)$, nämlich $S_0 → S_1 → S_0 → S_0 → S_1→ S_0 $. Wir verweisen auf die Musterlösung zur "Aufgabe 3.9Z".
Die Skizze für den BCJR–Algorithmus verdeutlicht die Gewinnung des extrinsischen $L$–Wertes für das dritte Symbol ⇒ $L_{\rm E}(3)$. Der relevante Bereich im Trellis ist schraffiert:
- Bei der Abarbeitung des Trellisdiagramms in Vorwärtsrichtung gewinnt man – in gleicher Weise wie bei Viterbi – die Metriken $\alpha_1, \ \alpha_2, \ \text{...}\hspace{0.05cm} , \ \alpha_5$. Zur Berechnung von $L_{\rm E}(3)$ benötigt man hiervon $\alpha_2$.
- Anschließend durchläuft man das Trellisdiagramm rückwärts (also von rechts nach links) und erhält damit die Metriken $\beta_4, \ \beta_3, \ \text{...}\hspace{0.05cm} , \ \beta_0$ entsprechend der unteren Skizze.
- Der gesuchte extrinsische $L$–Wert $L_{\rm E}(3)$ ergibt sich aus den Metriken $\alpha_2$ (in Vorwärtsrichtung) und $\beta_3$ (in Rückwärtsrichtung) sowie der Apriori–Information $\gamma_3$ über das Symbol $i = 3$.
Basic structure of concatenated coding systems
Die wichtigsten Kommunikationssysteme der letzten Jahre verwenden zwei unterschiedliche Kanalcodes. Man spricht dann von verketteten Codiersystemen (englisch: Concatenated Codes). Auch bei relativ kurzen Komponentencodes $\mathcal{C}_1$ und $\mathcal{C}_2$ ergibt sich für den verketteten Code $\mathcal{C}$ eine hinreichend große Codewortlänge $n$, die ja bekanntlich erforderlich ist, um sich der Kanalkapazität anzunähern.
Zunächst seien einige Beispiele aus dem Mobilfunk genannt:
- Bei GSM (Global System for Mobile Communications, zweite Mobilfunkgeneration) wird zunächst die Datenbitrate von $9.6 \ \rm kbit/s$ auf $12 \ \rm kbit/s$ erhöht, um auch in leitungsvermittelten Netzen eine Fehlererkennung zu ermöglichen. Anschließend folgt ein punktierter Faltungscode mit der Ausgangsbitrate $22.8 \ \rm kbit/s$. Die Gesamtcoderate beträgt somit etwa $42.1\%$.
- Beim 3G–Mobilfunksystem UMTS (Universal Mobile Telecommunications System) verwendet man je nach den Randbedingungen (guter/schlechter Kanal, wenige/viele Teilnehmer in der Zelle) einen Faltungscode oder einen Turbocode (darunter versteht man per se die Verkettung zweier Faltungscodierer). Beim 4G–Mobilfunksystem LTE (Long Term Evolution) verwendet man für kurze Kontrollsignale einen Faltungscode und für die längeren Payload-Daten einen Turbocode.
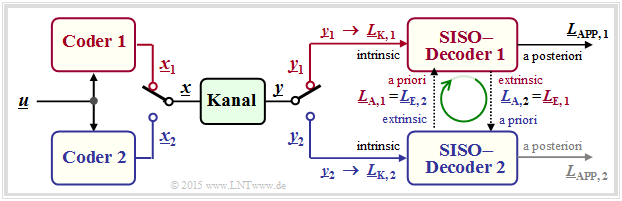
Die Grafik zeigt die Grundstruktur eines parallel verketteten Codiersystems. Alle Vektoren bestehen aus $n$ Elementen: $\underline{L} = (L(1), \ \text{...}\hspace{0.05cm} , \ L(n))$. Die Berechnung aller $L$–Werte geschieht also auf Symbolebene. Nicht dargestellt ist hier der Interleaver, der zum Beispiel bei den Turbocodes obligatorisch ist.
- Die Codesequenzen $\underline{x}_1$ und $\underline{x}_2$ werden zur gemeinsamen Übertragung über den Kanal durch einen Multiplexer zum Vektor $\underline{x}$ zusammengefügt. Am Empfänger wird die Sequenz $\underline{y}$ wieder in die Einzelteile $\underline{y}_1$ und $\underline{y}_2$ zerlegt. Daraus werden die Kanal–$L$–Werte $\underline{L}_{\rm K,\hspace{0.05cm}1} $ und $\underline{L}_{\rm K,\hspace{0.05cm}2}$ gebildet.
- Der symbolweise Decoder ermittelt entsprechend der vorne beschriebenen Vorgehensweise die extrinsischen $L$–Werte $\underline{L}_{\rm E,\hspace{0.05cm} 1}$ und $\underline{L}_{\rm E,\hspace{0.05cm} 2}$, die gleichzeitig die Apriori–Informationen $\underline{L}_{\rm A,\hspace{0.05cm} 2}$ und $\underline{L}_{\rm A,\hspace{0.05cm} 1}$ für den jeweils anderen Decoder darstellen.
- Nach ausreichend vielen Iterationen (also dann, wenn ein Abbruchkriterium erfüllt ist) liegt am Decoderausgang der Vektor der Aposteriori–Werte ⇒ $\underline{L}_{\rm APP}$ an. Im Beispiel wird willkürlich der Wert im oberen Zweig genommen. Möglich wäre aber auch der untere $L$–Wert.
Das obige Modell gilt insbesondere auch für die Decodierung der Turbo–Codes gemäß dem Kapitel Grundlegendes zu den Turbocodes.
Aufgaben zum Kapitel
Aufgabe 4.1: Zum „Log Likelihood Ratio”
Aufgabe 4.1Z: L–Werte des BEC–Modells
Aufgabe 4.2: Kanal–LLR bei AWGN
Aufgabe 4.3: Iterative Decodierung beim BSC
Aufgabe 4.3Z: Umrechnungen von L–Wert und S–Wert
Aufgabe 4.4: Extrinsische L–Werte beim SPC
Aufgabe 4.4Z: Ergänzung zur Aufgabe 4.4
Aufgabe 4.5: Nochmals zu den extrinsischen L–Werten
Aufgabe 4.5Z: Tangens Hyperbolikus und Inverse
Quellenverzeichnis