Difference between revisions of "Aufgaben:Exercise 4.08Z: Basics about Interleaving"
| Line 28: | Line 28: | ||
* Die Aufgabe bezieht sich auf das Kapitel [[Channel_Coding/The_Basics_of_Turbo_Codes| "The Basics of Turbo Codes"]]. | * Die Aufgabe bezieht sich auf das Kapitel [[Channel_Coding/The_Basics_of_Turbo_Codes| "The Basics of Turbo Codes"]]. | ||
| − | * | + | *But other $\rm LNTww$–books also discuss interleaving, including the book "Examples of Message Systems" with reference to the |
| − | :* Standard <i>Digital Subscriber Line</i> (DSL) ⇒ [[Examples_of_Communication_Systems/Methods_to_Reduce_the_Bit_Error_Rate_in_DSL#Interleaving_und_De.E2.80.93Interleaving| "Interleaving | + | :* Standard <i>Digital Subscriber Line</i> (DSL) ⇒ [[Examples_of_Communication_Systems/Methods_to_Reduce_the_Bit_Error_Rate_in_DSL#Interleaving_und_De.E2.80.93Interleaving| "Interleaving and Deinterleaving"]], |
| − | :* 2G | + | :* 2G mobile communication system GSM ⇒ [[Examples_of_Communication_Systems/Entire_GSM_Transmission_System#Komponenten_der_Sprach.E2.80.93_und_Daten.C3.BCbertragung| "Components of voice– and data transmission"]], |
| − | :* 3G | + | :* 3G mobile communication system UMTS ⇒ [[Examples_of_Communication_Systems/Telecommunications_Aspects_of_UMTS#Kanalcodierung_bei_UMTS| "Channel Coding"]], |
| − | :* 4G | + | :* 4G mobile communication system LTE ⇒ [[Mobile_Communications/The_Application_of_OFDMA_and_SC-FDMA_in_LTE#Functionality_of_SC-FDMA| "Funktionsweise von SC–FDMA"]] (in the book "Mobile Communications"). |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
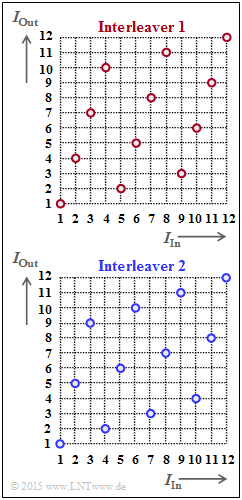
| − | { | + | {What interleaver–type is shown in the graphic on the details page? |
|type="()"} | |type="()"} | ||
| − | + Block | + | + Block interleaving, |
| − | - Random | + | - Random interleaving. |
| − | { | + | {How many rows ($Z$) and columns ($S$) does the upper "Interleaver matrix 1" have? |
|type="{}"} | |type="{}"} | ||
$Z \ = \ ${ 4 } | $Z \ = \ ${ 4 } | ||
$S \ = \ ${ 3 } | $S \ = \ ${ 3 } | ||
| − | { | + | {It holds $\underline{u} = (1001'0001'1101'1101'0010'0111)$. How does the scrambled sequence begin $\underline{u}_{\pi}$? <br> Note: The quotation marks serve only as a reading aid. |
|type="()"} | |type="()"} | ||
- $\underline{u}_{\pi} = (110'100'100'011'111'110'010'001' \text{...}\ )$, | - $\underline{u}_{\pi} = (110'100'100'011'111'110'010'001' \text{...}\ )$, | ||
+ $\underline{u}_{\pi} = (101'001'000'111'100'101'011'101'\text{...}\ )$. | + $\underline{u}_{\pi} = (101'001'000'111'100'101'011'101'\text{...}\ )$. | ||
| − | { | + | {The scrambled sequence be $\underline{u}_{\pi} = (100'100'011'101'110'100'100'111)$. What is the sequence after deinterleaving? |
|type="()"} | |type="()"} | ||
+ $\underline{u} = (1101'0010'0011'1111'1001'0001'\text{...}\ )$, | + $\underline{u} = (1101'0010'0011'1111'1001'0001'\text{...}\ )$, | ||
| Line 60: | Line 60: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | [[File:P_ID3041__KC_Z_4_8b_v2.png|right|frame| | + | [[File:P_ID3041__KC_Z_4_8b_v2.png|right|frame|4×3 Interleaver Matrix]] |
| − | '''(1)''' | + | '''(1)''' From the regular structure of the function $I_{\rm Out}(I_{\rm In})$ one can see that it is a block interleaver ⇒ <u>Response 1</u>. |
| − | '''(2)''' | + | '''(2)''' The index "1" is output as the first character. Further applies: |
| − | * | + | * The index 5 is output as the second character ⇒ $\underline{Z = 4}$. |
| − | * | + | * The index 2 is output as the fourth character ⇒ $\underline{S = 3}$. |
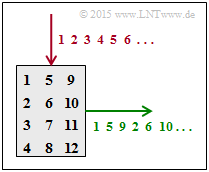
| − | + | The upper graph shows for the 4×3 interleaver matrix: | |
| − | * | + | * the column by column write (red), |
| − | * | + | * the row by row readout (green). |
| − | [[File:P_ID3042__KC_Z_4_8c_v3.png|right|frame| | + | [[File:P_ID3042__KC_Z_4_8c_v3.png|right|frame|Interleaving]] |
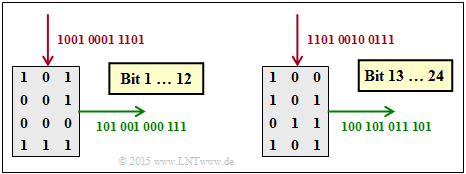
| − | '''(3)''' | + | '''(3)''' Correct is <u>the proposed solution 2</u>: |
| − | * | + | *The matrix is written column by column and read row by row. |
| − | * | + | *After 12 bits, the matrix is cleared and the procedure starts over. |
| − | * | + | *The graphic shows that now the solution suggestion 2 is correct. |
<br clear=all> | <br clear=all> | ||
[[File:P_ID3043__KC_Z_4_8d_v1.png|right|frame|Zum De–Interleaving]] | [[File:P_ID3043__KC_Z_4_8d_v1.png|right|frame|Zum De–Interleaving]] | ||
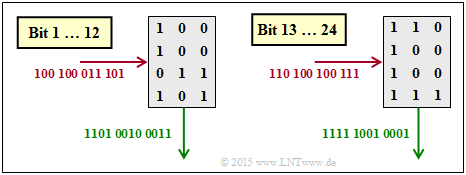
| − | '''(4)''' | + | '''(4)''' Correct is <u>the proposed solution 1</u>: |
| − | * | + | *In deinterleaving, the matrix is written row by row and read column by column. |
| − | * | + | *The graphic shows that here the solution suggestion 1 is correct. |
Revision as of 19:01, 29 November 2022
Interleaving is required, for example, for a channel with burst error characteristics in order to distribute the errors within the burst over a sufficiently large area so that they can subsequently be largely corrected (or at least detected).
For turbo codes based on so-called RSC encoder (Recursive Systematic Convolutional Encoder) – and only such make sense – interleaving is essential also with the AWGN channel, because then there are also always (some) input sequences, which deliver only zeros in the output sequence after quite a few ones, and that to infinity ⇒ there are output sequences with very small Hamming weight.
If the bits of such input sequences are distributed over a wide range in the second coder, the problem can be (largely) eliminated by the interaction of both component decoders in the case of iterative symbol-wise decoding.
A general distinction is made between
- Block interleaver and
- Random interleaver.
In block interleaving one fills a matrix with $S$ columns and $Z$ rows column by column and reads the matrix row by row. This deterministically scrambles a block of information with $I_{\rm max} = S \cdot Z$ bits.
On the right, two interleavers are indicated and in graphical form by the assignment $I_{\rm Out}(I_{\rm In})$. These quantities represent the "index of the output sequence" and the "index of the input sequence", respectively. It holds:
- $$1 \le I_{\rm Out} \le I_{\rm max} \hspace{0.05cm}, \hspace{0.5cm} 1 \le I_{\rm In} \le I_{\rm max} \hspace{0.05cm}. $$
In the subtask (1) it is asked whether this is block interleaving or random interleaving . The latter are discussed in the "theory section" but only very briefly.
Hints:
- Die Aufgabe bezieht sich auf das Kapitel "The Basics of Turbo Codes".
- But other $\rm LNTww$–books also discuss interleaving, including the book "Examples of Message Systems" with reference to the
- Standard Digital Subscriber Line (DSL) ⇒ "Interleaving and Deinterleaving",
- 2G mobile communication system GSM ⇒ "Components of voice– and data transmission",
- 3G mobile communication system UMTS ⇒ "Channel Coding",
- 4G mobile communication system LTE ⇒ "Funktionsweise von SC–FDMA" (in the book "Mobile Communications").
Questions
Solution
(1) From the regular structure of the function $I_{\rm Out}(I_{\rm In})$ one can see that it is a block interleaver ⇒ Response 1.
(2) The index "1" is output as the first character. Further applies:
- The index 5 is output as the second character ⇒ $\underline{Z = 4}$.
- The index 2 is output as the fourth character ⇒ $\underline{S = 3}$.
The upper graph shows for the 4×3 interleaver matrix:
- the column by column write (red),
- the row by row readout (green).
(3) Correct is the proposed solution 2:
- The matrix is written column by column and read row by row.
- After 12 bits, the matrix is cleared and the procedure starts over.
- The graphic shows that now the solution suggestion 2 is correct.
(4) Correct is the proposed solution 1:
- In deinterleaving, the matrix is written row by row and read column by column.
- The graphic shows that here the solution suggestion 1 is correct.