Objectives of Modulation and Demodulation

From LNTwww

  1. Modulation Methods
  2. General Description
  3. Objectives of Modulation and Demodulation

# OVERVIEW OF FIRST MAIN CHAPTER #


This book deals with Modulation and Demodulation , two classical and important methods for communications engineering, which already have a very long tradition but are nevertheless constantly developing. 

Before analog amplitude and angle modulation are described in detail in the following chapters, along with today's more relevant digital modulation methods, this first chapter introduces the definitions and descriptive variables which are equally valid for all systems. 

This chapter deals in detail with:

  • the objectives  of Modulation and Demodulation,
  • the differences and similarities between analog  and digital  modulation techniques,
  • the signal-to-noise power ratio  as a very general quality criterion,
  • linear  and non-linear distortions  due to modulation/demodulation,
  • degradation in the presence of stochastic interference,  such as noise,
  • a unified model  for describing amplitude and angle modulation,
  • descriptions using the analytical signal  and the equivalent low–pass signal.

The message transmission system under consideration


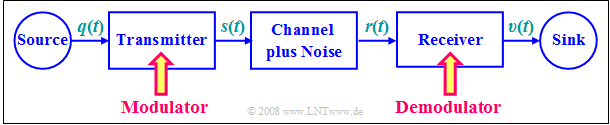
The message transmission system considered in the book "Modulation Methods"

Throughout the book "Modulation Methods", we will be base our message transmission system on the block diagram shown here.

The transmission medium (the physical transmission channel) is characterised here by its  frequency response $H_{\rm K}(f)$ . We will consider:

  • electrical lines  (coaxial cable, twisted pair, etc.), 
  • optical fibres  (multimode or single mode),
  • radio connections  (directional radio, satellite radio, mobile radio, etc.).


Further considerations:

  • Let the source signal  $q(t)$  be an analog signal, for example, speech, music or the (analog) output of a camera.  Let the corresponding spectrum  $Q(f)$  lie in the frequency range  $|f| ≤ B_{\rm LF}$ , where the subscript stands for "low frequency".
  • The middle block in the above figure also includes interference (interference, crosstalk from other users, impulse interference from power lines, etc.) and noise sources such as thermal and semiconductor noise.  These are captured by the interference power density spectrum  ${\it Φ}_n(f)$.
  • The task of such a message transmission system is to transmit the message or information contained in the source signal  $q(t)$  – note the different meaning of these quantities  – to the spatially distant sink, with the proviso that the sink signal $v(t)$  differs "as little as possible" from  $q(t)$.
  • A common problem is that the channel is unsuitable for direct transmission of the source signal $q(t)$ because it contains "unfavourable frequencies". For example, a music signal with frequencies up to about $\text{15 kHz}$  cannot be transmitted directly by radio, since radio propagation is only possible from around $\text{100 kHz}$.
  • The only solution here is a signal conversion at the transmitter known as modulation.  The output signal of the modulator will be uniformly referred to as the transmission signal  $s(t)$  in the following.  This is generally at higher frequencies than the source signal  $q(t)$.
  • Demodulation  is the signal reset at the receiver to recover the low frequency sink signal  $v(t) ≈ q(t)$  from the high frequency received signal  $r(t)$ . With real channels, the desired result $v(t) \equiv q(t)$  is not possible due to the noise  $n(t)$ that is always present.


Adapting to the transmission channel and interference spectrum


The primary task of modulation (in the sense meant here) is adding a higher frequency carrier signal with carrier frequency  $f_{\rm T}$ to shift the message signal to a different frequency position,

  • with a more favourable frequency response $H_{\rm K}(f)$  and/or
  • with a more favourable interference power density spectrum ${\it Φ}_n(f)$.


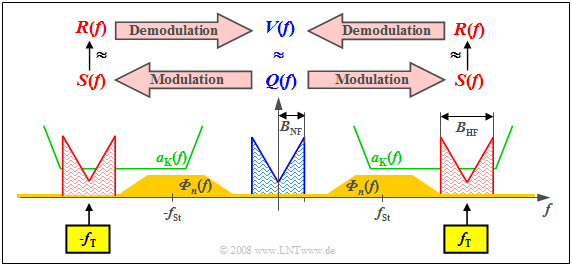
$\text{Example 1:}$  The graph shows the low-frequency spectrum $Q(f)$ with bandwidth  $B_{\rm NF}$ in blue. The attenuation curve  $a_{\rm K}(f) = \ –\ln \ \vert H_{\rm K}(f) \vert $  of the channel is plotted in green, which here shows favourable characteristics with constant low attenuation in a sufficiently large frequency range.

Illustrating modulation and demodulation

In yellow, you can see the interference power density spectrum ${\it Φ}_n(f)$, which does not disappear throughout the frequency range due to thermal noise and, in our constructed example, takes on particularly large values around frequency $f_{\rm St}$  due to external interference.

These boundary conditions make clear:

  • One must select the carrier frequency  $f_{\rm T}$  approximately as drawn so that  $S(f)$  can be transmitted in the best possible way with respect to distortion and interference/noise. This results in a frequency band of sufficient quality with width  $B_{\rm HF} = 2 · B_{\rm NF}$.
  • This shift of the source signal spectrum  $Q(f)$  by the carrier frequency  $f_{\rm T}$  to the right – and also by the same distance to the left due to the system-theoretical approach of bilateral frequencies – represents  modulation.
  • Demodulation, on the other hand, is signal conversion in the opposite direction. Starting from the received spectrum  $R(f)$, which differs at least slightly from the transmitted spectrum  $S(f)$  due to attenuation and noise, one arrives at the spectral function  $V(f) ≈ Q(f)$.


Further reasons for modulation/demodulation are given in the following sections.

Channel bundling – frequency division multiplexing


Another advantage of modulation with a harmonic oscillation as a carrier signal is that a single transmission channel of sufficient bandwidth can be used by several signals simultaneously. One then speaks of

  • Frequency Division Multiplexing  (FDM)
  • or Frequency Division Multiple Access  (FDMA).


The principle of multiplexing

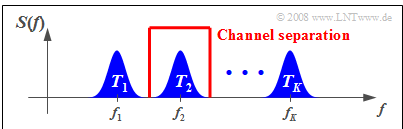
The diagram illustrates the situation.  $K$  message signals are to be transmitted simultaneously via a physical channel of appropriate bandwidth. The subchannels are marked here with  $T_1$, ... , $T_K$ . One proceeds as follows:

  • One modulates the source signals  $q_1(t)$,  $q_2(t)$, ... ,  $q_K(t)$  of users with different carrier frequencies  $f_1$,  $f_2$, ... ,  $f_K$.
  • One combines the transmission signals  $s_1(t)$,  $s_2(t)$, ... ,  $s_K(t)$  to form a total signal 𝑠(𝑡), enabling multiple use of the transmission set-up.
  • To demodulate the source signal  $q_k(t)$ , one uses the special carrier frequency  $f_k$.  Subsequent filtering achieves   $v_k(t) = q_k(t)$  (but only with negligible noise interference). This process is called channel separation.


$\text{Example 2:}$  Frequency division multiplexing has been used for many decades in analog TV and radio transmission.

  • This allows a sufficient number of programs to be accommodated, for example in the UHF band  $($frequencies between $\text{470 MHz}$ and $\text{850 MHz)}$  more than forty TV programs have a channel spacing of  $\text{8 MHz}$.
  • However, since around 2004, analog TV transmission in this frequency band has been increasingly displaced by the new digital video standard  Digital Video Broadcast – Terrestrial  (DVB–T), which also uses FDMA.


$\text{Beispiel 3:}$ 

  • In der optischen Übertragungstechnik bezeichnet man dieses FDMA–Verfahren als  Wellenlängenmultiplex  bzw.  Wave–length Division Multiplex  (WDM).
  • Damit kann man derzeit (2005) über einen einzigen Lichtwellenleiter gleichzeitig  $160$  Digitalsignale à  $\text{10 Gbit/s}$  übertragen   ⇒   Gesamtbitrate:  $\text{1.6 Tbit/s}$.

Analoges Übertragungssystem vs. digitales Übertragungssystem


Für das gesamte Buch "Modulationsverfahren" wird vorausgesetzt, dass das Quellensignal  $q(t)$  und das Sinkensignal  $v(t)$  jeweils Analogsignale seien.

  • Sie können also sowohl zeitkontinuierlich als auch wertkontinuierlich sein.
  • Damit ist aber noch nicht festgelegt, ob die eigentliche Übertragung analog oder digital erfolgt.


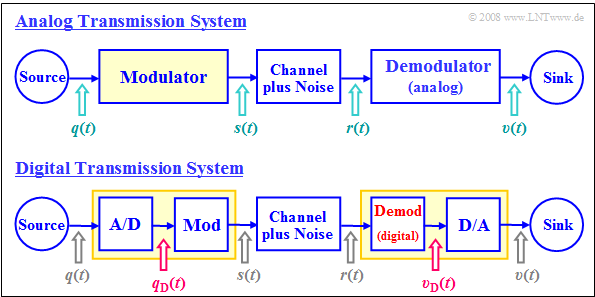
Analoges Übertragungssystem (oben) und digitales Übertragungssystem (unten)

Die beiden Blockschaltbilder verdeutlichen die wesentlichen Unterschiede zwischen einem analogen und einem digitalen Nachrichtenübertragungssystem.

Man erkennt:

  • Bei analoger Modulation ist das modulierende Signal  $q(t)$  immer ein Analogsignal und damit sowohl wert– als auch zeitkontinuierlich.
  • Dagegen ist bei digitaler Modulation das Eingangssignal  $q_{\rm D}(t)$  des Modulators stets digital, also sowohl wertdiskret als auch zeitdiskret.
  • Bei digitaler Modulation eines analogen Audio– oder Videosignals  $q(t)$  muss dieses zunächst A/D–gewandelt werden:  $q(t) \ \rightarrow \ q_{\rm D}(t)$.
  • Funktional unterscheidet sich der Modulator des Digitalsystems  $\rm (Mod)$  nicht vom Modulator des analogen Übertragungssystems.
  • Die beiden Demodulatoren unterscheiden sich aber prinzipiell:  Der obere liefert das Analogsignal  $v(t)$, der untere das Digitalsignal  $v_{\rm D}(t)$.
  • Nach der digitalen Übertragung eines Analogsignals – beispielsweise Audio oder Video – muss somit noch eine D/A–Wandlung erfolgen.


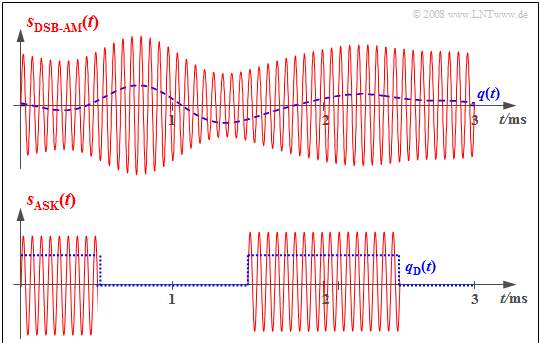
$\text{Beispiel 4:}$  Die beiden Grafiken zeigen die jeweiligen Eingangssignale (jeweils blau gestrichelt) und Ausgangssignale (durchgehend rot) des Modulators bei einem analogen und einem digitalen Übertragungssystem.

Beispielhafte Signale bei analoger und digitaler Amplitudenmodulation
  • Beim analogen Übertragungssystem (oben) steckt die Information über das analoge Quellensignal  $q(t)$  direkt in der Amplitude (Hüllkurve) des modulierten Signals  $s(t)$.  Es handelt sich hierbei um das analoge Modulationsverfahren  Zweiseitenband–Amplitudenmodulation mit Träger.
  • Die untere Grafik bezieht sich auf  Amplitude Shift Keying  (ASK), die digitale Variante der Amplitudenmodulation. Hier ist das Modulatoreingangssignal  $q_{\rm D}(t)$  digital und aus dem analogen Quellensignal $q(t)$ durch Abtastung, Quantisierung und PCM–Codierung entstanden.
  • Das modulierte Signal  $s(t)$  zeigt, dass der Modulator auch beim digitalen Übertragungssystem eine ähnliche Funktionalität aufweist wie beim (oberen) analogen Übertragungssystem.


Analoge Modulationsverfahren haben derzeit (2005) vor allem für die Verbreitung von Rundfunk– und Fernsehprogrammen noch eine gewisse Bedeutung, werden aber auch in diesem Bereich mehr und mehr durch entsprechende Digitalverfahren verdrängt. Trotzdem nehmen die Analogverfahren in  diesem Buch  einen breiteren Raum ein:


$\text{Die Gründe hierfür sind:}$

  • Aufgrund der hohen Kosten bei der Umrüstung bestehender sowie der Einführung neuer Systeme werden auch für die Analogsysteme noch längere Laufzeiten prognostiziert.
  • Viele Komponenten eines Analogsystems werden ebenso bei den digitalen Modulationsverfahren benötigt, zum Beispiel der in beiden Varianten verwendete Synchrondemodulator.
  • Die typische Vorgehensweise bei der Untersuchung nachrichtentechnischer Aspekte lässt sich bei Analogsystemen umfassender – und oft auch verständlicher – erklären als bei Digitalsystemen.


Zur Entwicklung der analogen Modulationsverfahren


Es folgen einige Daten zur geschichtlichen Entwicklung der analogen Modulation.  Meilensteine für die Entwicklung der analogen Modulationsverfahren auf Trägerfrequenzbasis waren:

  • die Einführung des regulären Rundfunkdienstes  (1923),
  • der Beginn der Trägerfrequenztelefonie  (1923),
  • die Einführung des regulären Fernsehdienstes  (1935),
  • die erste Satellitenübertragung  (1945),
  • die Einführung des NTSC–Farbfernsehens  (1953),
  • die Einführung des PAL–Farbfernsehens  (1967).


Voraussetzungen für diese Entwicklungen waren unter Anderem folgende Erfindungen in der Vergangenheit:

Vorteile der digitalen Modulationsverfahren


Die Vorteile der digitalen Modulationsverfahren sind vielfältig:

  • Die Realisierung eines Digitalsystems kann ebenfalls digital erfolgen und die Schaltungen sind in hohem Maße integrierbar (VLSI – Very Large Scale Integration).
  • Die Übertragungsqualität ist meist sehr gut, da sich (Rausch–)Störungen nur dann bemerkbar machen, wenn sie größer als ein vorgegebener Schwellenwert sind.
  • Wegen der möglichen Signalregenerierung in regelmäßigen Abständen durch so genannte Regeneratoren können sehr große Entfernungen mit hinreichend guter Übertragungsqualität überbrückt werden.
  • Die Datenübertragung – zum Beispiel zwischen Server und Client – bietet sich in digitaler Form an, da jedes Datensignal bereits digital ist.  Analogsignale müssen vor der Übertragung digitalisiert werden.
  • Durch die einheitliche Übertragung von Sprach–, Bild– und Datensignalen ist es möglich, ein gemeinsames und leistungsfähiges Netz für viele Telekommunikationsdienste aufzubauen.
  • Es existieren einfache und sehr effiziente Verschlüsselungs– und Datensicherungsmechanismen für Digitalsignale, was eine wichtige Voraussetzung für sicherheitskritische Anwendungen ist.
  • Bei einem Digitalsystem können – eventuell zusätzlich zu Frequenzmultiplex – auch die Vorteile von Zeitmultiplexverfahren genutzt werden, die nachfolgend beschrieben werden.


Alle in den letzten Jahren entwickelten Systeme sind digital, zum Beispiel:

  •   Compact Disc   (CD) – digitales Speichermedium  (Philips, 1982),
  •   Digital European Cordless Telephone   (DECT) – schnurloses Telefon  (1992),
  •   Global System for Mobile Communication   (GSM) – europäisches Mobilfunksystem  (1992),
  •   Integrated Services Digital Network   (ISDN) – digitales Telefonnetz  (in Europa 1993),
  •   Digital Audio Broadcast   (DAB) – digitaler Rundfunk  (2001),
  •   Digital Video Broadcast   (DVB) – digitales Fernsehen  (2002),
  •   Digital Subscriber Line   (DSL) – schnelle Rechnerkopplung  (2002),
  •   Universal Mobile Telephone System  UMTS) – Mobilfunk der 3. Generation (2003),
  •   Long Term Evolution   (LTE) – Mobilfunk der 4. Generation  (2011).


Die Zahlen in Klammern geben jeweils die Jahreszahl des ersten Einsatzes an.  Meistens hat es von der Erfindung über die Standardisierung bis hin zur Entwicklung eines einsatzfähigen Systems mehr als ein Jahrzehnt gedauert.

  • In vierten Hauptkapitel  dieses Buches  sind die digitalen Modulationsverfahren zusammenfassend dargestellt.
  • Eine detaillierte Beschreibung  (Berechnung der Fehlerwahrscheinlichkeit, Aspekte der Systemoptimierung, usw.)  finden Sie im Buch  Digital Signal Transmission.

Zeitmultiplexverfahren


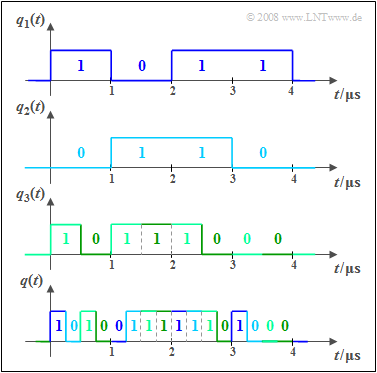
Bei einem Digitalsystem kann zur gemeinsamen Nutzung eines Übertragungskanals durch mehrere Nutzer neben Frequenzmultiplex auch die Zeitmultiplextechnik eingesetzt werden.  Die Grafik soll das Prinzip an einem Beispiel verdeutlichen:

Zur Verdeutlichung von Zeitmultiplex
  • Die Signale  $q_1(t),   q_2(t)$  und  $q_3(t)$  sind binär und werden durch Amplitudenkoeffizienten  $(0$ oder $1)$  vollständig beschrieben.  Es liegt eine  zeitdiskrete Signaldarstellung  vor  $($Symboldauer  $T = 1\ \rm µ s)$.
  • Für die Bitraten dieser beiden ersten Signale gilt jeweils  $R_1 = R_2 = 1/T = \text{1 Mbit/s}$.  Dagegen ist die Bitrate von  $q_3(t)$  doppelt so groß, also  $R_3 = \text{2 Mbit/s}$.
  • Unten dargestellt ist das gemeinsame Zeitmultiplex–Ausgangssignal  $q(t)$  mit der Gesamtbitrate  $R = R_1 + R_2 + R_3 = \text{4 Mbit/s}$.  Der Bezug zu den Eingangssignalen ist farblich gekennzeichnet.
  • Nach der Übertragung von  $q(t)$  über den physikalischen Kanal müssen die Teilsignale  $v_1(t)$, ... ,  $v_3(t)$  beim Empfänger wieder getrennt werden.  Man nennt diese Funktionseinheit den  Demultiplexer.
  • In der Praxis erfolgt das Multiplexen meist nicht bitweise, sondern den Teilnehmern werden in einem festen Raster Zeitschlitze zur Verfügung gestellt, in denen Bitrahmen übertragen werden.

Aufgaben zum Kapitel


Aufgabe 1.1: Multiplexing beim GSM–System

Aufgabe 1.1Z: UKW-Rundfunk



Retrieved from "http://en.lntwww.de/index.php?title=Modulation_Methods/Objectives_of_Modulation_and_Demodulation&oldid=42431"
  • Powered by MediaWiki